高中數學圓錐曲線部分學習障礙應對策略研究

陳小峰

(江蘇省如東高級中學 226400)

一、注重基礎知識的推導與構建過程的學習

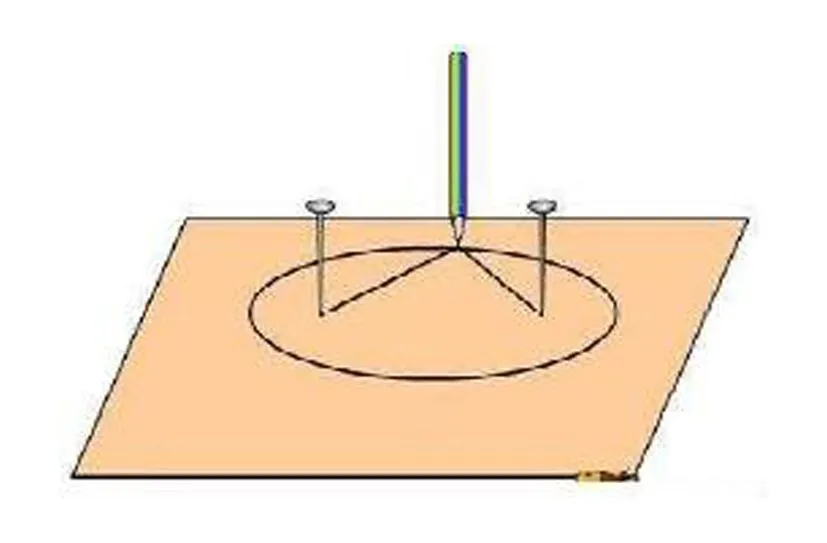
在圓錐曲線的教學中要注重基礎知識的推導，切忌出現死記硬背知識的情況，要將相關定義、性質的推導過程教給學生，加深他們對相關知識的理解.期間，可以采用小組合作的方式來引導學生進行基礎知識的推導活動，讓所有學生都能夠參與教學活動當中.同時，教師還可以借助相關的教學用具輔助學生推導相關的知識.例如，在學習橢圓的定義時，教師可以利用繩子、鉛筆來繪畫運動軌跡，讓學生體驗橢圓的定義.

另外，教師還要注重學生基礎知識構建過程的學習，教師不能夠單純地將所要學習的知識搬運給學生就可以了，而是要將知識內部之間的聯系一并教授給學生，讓學生掌握圓錐曲線部分的知識體系，能夠將新學習的知識點與已學習的知識點有機地結合起來，提高知識的遷移能力和自己對知識的理解能力.這就要求教師在教學過程當中，要注重知識邏輯性的講述，可以通過思維導圖的形式，引導學生去構建知識體系.通過思維導圖將三種不同的圓錐曲線的異同之處直觀地呈現出來，每學完一種圓錐曲線就構建一個詳細的思維導圖.學生在這個構建的過程中不僅能夠加深對知識的理解，還能夠形成完善的知識體系，更有利于學生后期對該部分知識的學習.

1.注重學生運算能力的培養

通過多年的教學實踐發現，學生之所以反映該部分知識學習困難，除了相關的性質定理困擾他們以外，較大的的計算量也是一個重要的因素.圓錐曲線部分的題目對學生計算能力要求較高，很多學生缺乏良好的運算習慣和解題方法，導致在圓錐曲線部分的學習中存在學習障礙.

首先，教師在平時的課堂教學過程中，要做好示范作用，在黑板上的板書要充分體現出自己的計算過程，讓學生能夠做到有章可循.同時，教師要及時地對學生作業中的解題進行批改和點評，對學生的計算問題及時地給予糾正.

其次，進行定時訓練.很多學生在平時的練習中存在“一看就知道”“很簡單不用寫”的情況，到考試的時候，一緊張就會暴露出各種問題，這就是沒有時間觀念的練習并不能夠對提高學生計算能力有很好的效果，因此，定時訓練非常重要.讓學生在有限的時間內，完成布置的練習題，通過適量的練習，學生的運算能力才能有所提升.

第三，引導學生正確使用錯題本和草稿本，錯題本和草稿本是學生返回檢查自身計算情況的重要載體，它能夠幫助學生更加快速地找出自己的問題所在，有針對性地進行復習.

2.注重數學思想的滲透

高中數學知識種類繁多，但是數學思想貫穿始終，是數學學習的精髓所在，也是學生解決數學問題的重要工具.在圓錐曲線部分，題目的綜合性和靈活性較強，如果教師僅僅依靠題海戰術讓學生去練習，難以取得明顯的效果，一旦碰上形式較為新穎的問題，學生就難以入手.這就要求教師在圓錐曲線的教學中要注重數學思想的滲透，提高學生利用數學思想方法來解決問題的能力.具體可以通過以下幾個方面來完成：

首先，培養學生良好的數學思維.在圓錐曲線的教學中，適當融入相關的數學文化，讓學生通過了解內涵的數學文化，去感受數學思想，培養自身的數學思維.

其次，培養學生數形結合的習慣.數形結合思想是圓錐曲線部分重要的數學思想，借助這一思想，學生能夠快速找到解題的突破口，高效地完成解題.在教學中，教師要有意識地訓練學生的作圖意識，可以利用課余時間組織學生開展作圖比賽，培養學生的作圖習慣.同時，還可以做專題的數形結合訓練，讓學生通過練習題去總結.

例1 設橢圓9x2+16y2=144的左右兩個焦點分別是F1和F2,經過點F1的直線與橢圓相交于A,B，那么△ABF2的周長是( ).

A.16 B.32 C.64 D.不確定

這一個題目就是一個典型的需要數形結合才能夠快速求解的題目.拿到題目后如果不去畫圖就很難找到解題的突破口，通過畫圖后，發現所求的三角形的周長實質上就是要去求橢圓上A,B兩點到F1和F2的距離之和.而橢圓上的點到兩個焦點的距離之和就是長軸的長度，這樣問題就可以迎刃而解了.

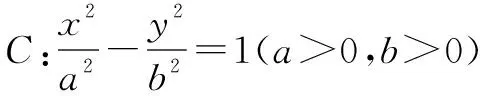
單純分析問題很難發現解決問題的思路，借助數形結合，就可以直觀地發現問題的突破口.

再次，要培養學生分類討論的思想意識，在課堂教學中，要對這部分的問題反復強調.

這一問題就需要學生去進行分類討論，焦點在坐標軸上還要分為在x軸，還是在y軸上，因此，要對它進行分類討論.

圓錐曲線部分是高中數學教學的重要組成部分，該部分知識能夠融合多部分數學知識，形成綜合性問題，考查學生的數學綜合能力，是學生數學學習中的一個重點也是難點.在教學中，教師要注重基礎知識的推導與構建過程的學習；注重學生運算能力的培養；注重數學思想的滲透，這樣才能夠提高學生解決圓錐曲線部分問題的能力，才能夠提高學生數學考試成績.