基于學生能力發展的教學思考與嘗試

王新星

(江蘇省通州高級中學 226300)

一、問題提出

師：很多同學在參數范圍問題的求解上表現得思路不清、計算模糊、解題不規范，今天我們就這一問題作詳細探討.

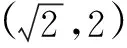
請各學生小組討論并由各組代表展示交流成果.

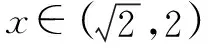
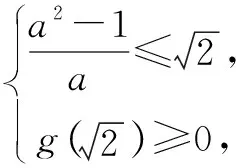
師：這是慣常所用的數形結合法，生1的思路與表達都是值得肯定的，不過運算量大也導致無法得到最終結果，大家想一想參數范圍問題可有更好解法呢？

生2：一般都用分離參數法，但本題的參數因為含有a2而無法直接分離出，此法對本題也不適合.

師：可有辦法將參數分離呢？

生3：進行整體分離，例如，m2+m≥2sinx對x∈R恒成立，m的取值范圍可以求得.

師：很好，大家都來試試看.

二、方法嘗試

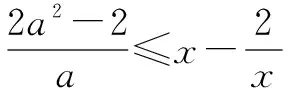
師：分析深入，條理清晰，非常好，大家可否對上述解題過程談談體會呢？

生5：分離參數的意識在解決此類問題時是必須的，整體分離解決本題時也表現出了解題的靈活性.

師(追問)：那么參數不好分離的情況是否還有呢？

生6：參數的系數符號不確定時就不能直接分離參數，例如：mx≤2x2+1，x∈R恒成立，求m的范圍.不等號的方向在分離參數時并不確定，應怎么辦呢？

三、思維發展

師：此時可以通過分類來解決問題，大家再看以下一題.

問題2 設函數f(x)=ax3-3x+1，若x∈[-1,1]時，f(x)≥0恒成立，求實數a的取值范圍.

這是一道涉及眾多知識與思想方法的綜合題，教師在此題的教學中應進行充分的預設并啟發學生的思維.

學生展示：

生7：因為x∈[-1,1]，因此分三種情況進行討論：

(1)若x=0，f(x)=1≥0恒成立；

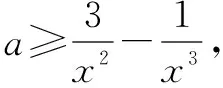
綜合(1)(2)(3)，可得a=4.

師：大家解決上述兩題之后可有什么收獲和感受呢？

生8：很多問題的解決中雖有方法，但因為特定環境的改變會存在新的問題，改變思維方式并想辦法進行克服才能更好地解決問題.

師：分離參數中一旦產生新的問題就需要解題的決心與能力作為支撐了.

問題3 設f(x)是定義在x∈[-1,1]上的奇函數，函數g(x)和f(x)的圖象關于y軸對稱，且當x∈[0,1]時，g(x)=lnx-ax2. (1)求函數f(x)的解析式；(2)若對于區間(0,1]上任意x都有|f(x)|≥1成立，求實數a的取值范圍.

師：處理|f(x)|≥1是解決本題的關鍵，去絕對值符號采用平方法還是絕對值定義是需要考慮的.

生9：平方比較復雜.

師：那大家趕緊來解題吧.

四、能力提升

師：從上題可知，分離參數在包含絕對值不等式恒成立的問題中照樣可以進行，借鑒這一思維也可以對含有二元變量方程的有解問題進行分析和處理，就是分離其中一個變量并用另一個變量表示，再結合其它條件進行解的判斷與求值.

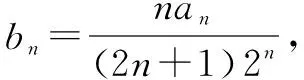
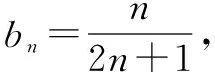
師：n到此處是否已經分離到位了呢？如果沒有，又該怎樣繼續呢？

師：很好，分離到位了，解題就不難了，由此可見，分離參數是數學方法、思想和能力的綜合.

總之，教師在具體教學中應不斷為學生創設探究的機會并將其貫穿于整個高中數學教學中，唯有如此學生的能力與素養才能獲得最大化的發展.