例談高中數學數形結合解題法教學的有效策略
王婷婷
(江蘇省南京市文樞高級中學 210004)
一、數學學習中數形結合應用的重要意義
1.數學學科中重要思維的學習掌握
在高中的數學學習中,幾何與代數的概念之間已經出現了明顯的分野,需要運用一種統一的思想概念將二者進行協調以及統一.在這種情況下,數形結合概念的應用就十分的廣泛,既能夠在解決代數問題時,將不容易理解的抽象概念轉化為實際的圖象,幫助理解,同時在幾何問題的解決過程中,也可以利用代數的概念以及公式,讓問題易于解決以及計算.
2.對于學生學習的直接幫助
數形結合的這種方式在學生的學習過程中,對于兩個方面具有重要的意義.其一,在于學生學習信心的提升以及保持.由于在高中的數學學習中,難度得到了明顯的增加,許多學生由于對于數學問題的理解能力不足,導致數學的問題不能夠得到及時的理解以及解答,學習成績下降,從而打擊了學生的學習積極性.其二、在于學生學習效率的提升,這一點對于學生的總體學習至關重要.由于在高中階段的學習中,學習科目多,學習的難度增加,各個科目的學習都將會對于學生的學習造成壓力,數學問題的逐漸復雜化,使得學生有許多的精力花費在數學的學習上,從而缺少時間進行總體能力的提升,數形結合的思想極大地幫助學生提高學習效率.
二、數形結合的應用原則
1.相互轉化的原則
在數形結合概念的應用中,由于幾何問題難度較大,多重視于將代數問題的向幾何問題的方向轉化,從而忽略了幾何問題同樣可以通過抽象化的轉化,利用具體的概念,進行精確的解答.因此,在對于數形結合應用過程中,需要對于這一應用原則進行注意,在解題的過程中,不僅需要對抽象的問題具體化,同樣可以利用這一方式對于幾何問題經過抽象化處理.
2.精確轉化的原則
在數形結合概念的應用過程中,多是對于代數問題的圖象化轉化,在轉化的過程中,需要注意轉化圖象的準確性,以保持在解題的過程中,答案的準確程度.在實際的解題過程中,經常出現由于畫圖不準確,而導致解題的過程出現誤差,從而解題的結果不正確的情況.
3.原題解答的思路原則
在問題的解答中,互相的轉化過程,為能夠在具體解答中加以簡化,最終的解答思路以及解答的原則,都需要以原題為準,及時地進行思路的轉化轉變,完成對于問題本身的解答,不能夠脫離問題應用.因此,在對于問題的解答過程中,需要對于其中的數據等內容進行精確的分析,在圖形的構建過程中,需要保證圖象所應用數據的精確,在精確構圖的基礎上,對于題目的內容進行解答.
三、高中數學中數形結合的具體應用
1.代數問題的圖象轉化
由于在數學語言的應用中,分別有符號語言以及圖象語言兩種具體的表達方式.符號語言的表達優勢在于描述的精準度較高,可以對于問題進行精確的解答.在圖形語言的表達中,由于直觀形象的存在,可以通過對于圖象的觀察,直接地得到觀察的內容,在腦中形成具體的映射.因此,在解決抽象化程度較為高的問題時,利用圖象的方式幫助解題,能夠達成對于題目的正確理解,從而在圖形的幫助下,進行問題的解答.此外,在代數的圖象轉化的過程中,通過圖象的重新構建,也能夠使得學生在對于題目的理解中,加深印象,具有更加完善的理解效果,對于題目的成功解答具有直接的幫助.
例如: 在“若不等式(x-1)2 當 0 這一方式在幾何問題的解答過程中,是經常選擇的解答方式.在圖形的應用過程中,雖然具有較強的直觀性,然而由于圖象內容在具體的表達過程中,缺乏圖象符號的準確性以及邏輯性,對于問題的解答以及描述都不能夠僅憑圖象就進行判斷,因此需要對于這樣的情況進行符號語言的轉化.例如對于下題: 設f(x)=x2-2ax+2-a,當x在[-1,+∞)間取值的時候,f(x)>0恒成立,求a的取值范圍.本題就可以借助下圖列不等式組求解. 在應用的過程中,有許多的情況下需要將兩種轉化方式結合使用,在解題的過程中,根據已知的條件對于具體的未知部分進行答案的求解,在轉換的過程中,需要注意其中數字以及條件的準確性,使得題目能夠準確地呈現以及解答.在解決一些靜態函數問題的時候,可以通過坐標系加圖象的動態表達,對問題進行闡述,進而予以有效解決.圖象能夠形象、直觀地表達函數的不足,而函數解析式具有計算精準的特點,可以彌補圖象精準性不高的缺陷,通過兩者的結合運用,可以有效解決問題. 在高中數學的學習過程過程中,數形結合思想的運用屬于重要的數學能力的鍛煉以及培養,不僅在解題的過程中學生能夠體驗這一方式的便利性,同時在對于數學思維以及數學學科體系的構建中也具有重要的作用.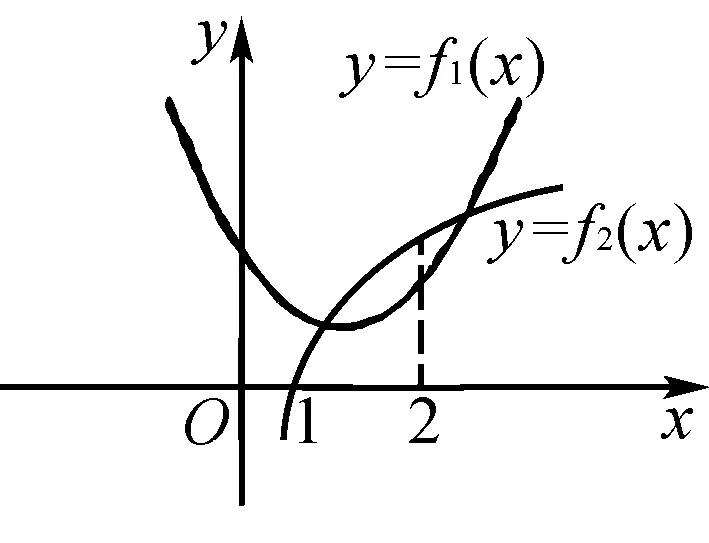
2.幾何問題的抽象轉化
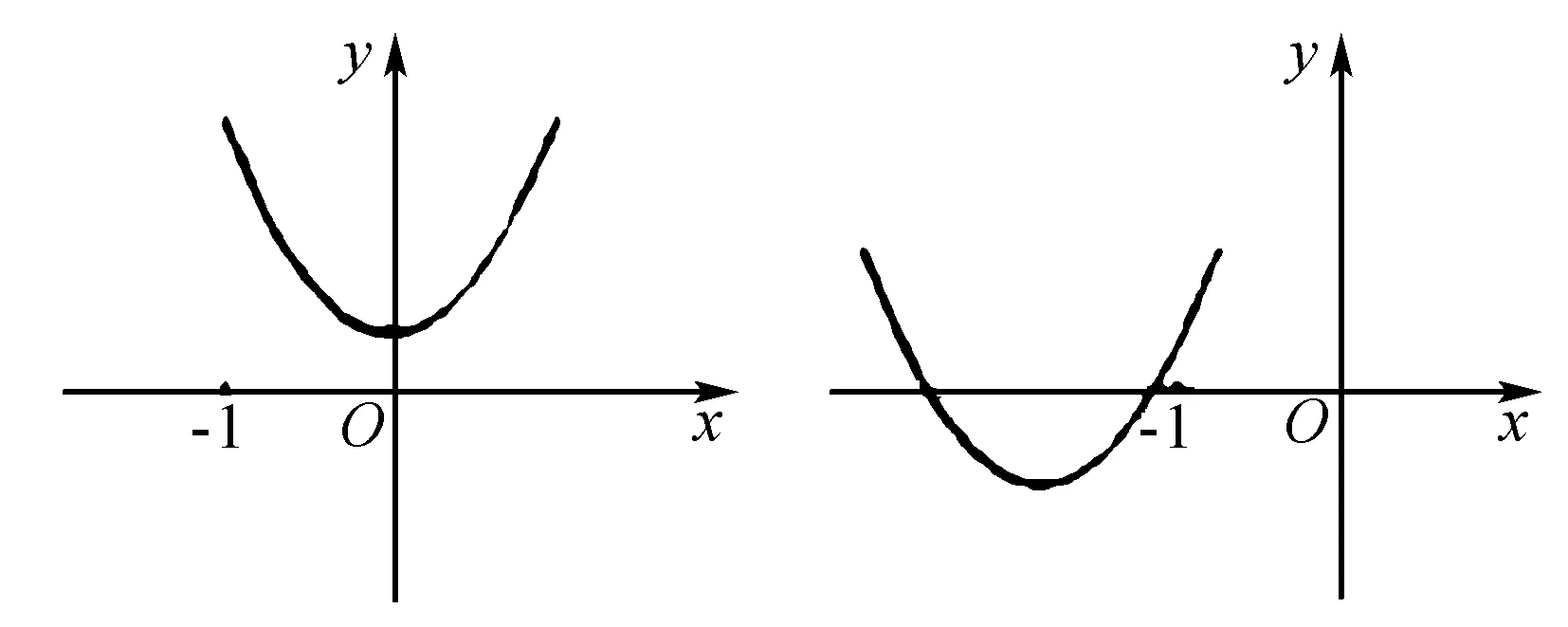
3.兩種方式間的相互轉化

