正畸托槽與弓絲間摩擦力性能的實驗研究

劉曉默，張夢琦，林久祥

（北京大學口腔醫院正畸科，北京 100081）

目前，輕力矯治的理念越來越受到正畸醫生的關注。托槽與弓絲之間的摩擦力貫穿于整個正畸治療的過程，研究顯示臨床上約50%～60%的正畸力要用來克服正畸過程中產生的摩擦力。減小摩擦力可以減輕患者的疼痛不適程度，降低牙根吸收和牙槽骨吸收潛在的風險，減少支抗丟失的可能性。正畸醫生有必要了解正畸過程中摩擦力的影響因素，以便在臨床治療上有的放矢，對牙齒施以適當的正畸力，以獲得牙齒及牙周等生物組織最佳反應及最佳矯治效果。

影響托槽和弓絲間摩擦力的因素很多，臨界角是關鍵因素之一。臨界角是牙齒發生傾斜至弓絲剛剛開始同時接觸槽溝齦牙合兩端時，托槽槽溝與弓絲之間的角度，是托槽與弓絲處于被動狀態和主動狀態交接點處的傾斜角度。當傾斜角未達到臨界角時，摩擦力基本保持恒定，僅為經典摩擦力，大小不隨傾斜角的變化而變化；當傾斜角達到臨界角后（弓絲未達到刻痕狀態之前） ，摩擦力包括經典摩擦力、約束摩擦力，大小隨傾斜角的增加而呈線性增大。

本研究擬應用自主研發的正畸摩擦力測試儀［1］，測試2種國產矯治器中的尖牙托槽與不銹鋼弓絲呈不同傾斜角度情況下的摩擦力大小，探索不同托槽-弓絲組合的最大被動狀態范圍及臨界角值。

1 材料與方法

1.1 實驗材料

選用中國杭州新亞公司的MBT普通金屬托槽和傳動直絲弓標準托槽 （第二代） 為研究對象，2種托槽均為0.022”系統，均選取上頜尖牙托槽作為研究對象，采用美國TP公司的彈力結扎圈結扎，傳動直絲弓標準托槽由于自身的“臺階”結構設計 （圖1） ，采用全結扎和斜結扎2種彈力結扎方式。測試弓絲選用0.016”不銹鋼圓絲和0.019”×0.025”不銹鋼方絲 （美國Plasdent公司） 。摩擦力測試儀的工作原理如圖2所示。

圖1 傳動直絲弓托槽的“臺階”結構Fig.1 Step structure of transmission straight archwire bracket

1.2 測試環境

每次實驗測試前，更換新的彈力結扎圈并等待5 min，以消除結扎圈彈力釋放不均對實驗結果造成的影響；更換新的托槽和弓絲，以消除磨損對實驗結果造成的影響；用95%乙醇棉球對托槽和弓絲進行脫脂處理，以消除各類附著物對實驗結果造成的影響。

通過尖牙托槽調節裝置中的手動角位臺，調整尖牙托槽槽溝與弓絲之間的傾斜角θ，θ角的大小在弓絲滑動過程中保持不變。由于2種托槽臨界角的理論計算值相差較大，實驗測定的θ角設定為2種范圍，MBT金屬托槽θ角設為0°、0.5°、1°、1.5°、2°、2.5°、3°、4°、5°、6°、7°、8°；傳動直絲弓標準托槽θ角設為0°、1°、2°、3°、4°、5°、6°、7°、8°、9°、10°、11°、12°、13°、14°、15°、16°、17°、18°、19°、20°、21°、22°、23°。分別測試不同θ角下，托槽與弓絲之間摩擦力的大小。實驗在干態環境室溫 （23 ℃±2 ℃） 下進行。

1.3 數據分析

本研究除了測試出不同托槽-弓絲組合的摩擦力大小外，還需統計分析不同托槽-弓絲組合的臨界角θ c。采用二階多項式回歸法計算臨界角 （θ c） ，該方法是本研究在分析既往研究的基礎上探索出的新方法。首先，構造二階多項式回歸模型N = a θ2+b θ+c（a為二次項系數，b為一次項系數，c為常數） ，以托槽槽溝與弓絲間的傾斜角 （θ） 為自變量，測得的力值（N） 為因變量，進行二階多項式回歸，得到第一個回歸方程。根據理論分析可知，當θ＜θ c時 （被動狀態范圍內） ，滑動摩擦力僅為經典摩擦力FR；當θ≥θ c時（主動狀態范圍內） ，滑動摩擦力等于FR與約束力BI之和，即FR+BI［2-3］。因此，θ＜θ c時的摩擦力可近似地由θ=0時測得的摩擦力來表示，即FR=c （c為第一個回歸方程中的常數項） 。在實驗的觀測力值中扣除c （即FR） 部分，得到的數值為BI。選擇觀測力值減去c后，仍穩定＞0的部分進行一元線性回歸，回歸模型為N = a θ+b，仍以托槽槽溝與弓絲間的傾斜角 （θ） 為解釋變量，測得的力值 （N） 為被解釋變量，得到第二個回歸方程，即為到達臨界角后摩擦力值與傾斜角形成的方程。第二個回歸方程的擬合線與N = c的交點對應的值就是臨界角θ c的數值，見圖3。

圖2 摩擦力測試儀工作原理圖Fig.2 Working principle of friction test instrument

圖3 二階多項式回歸法的分析模式Fig.3 Analysis paradigm of second-order polynomial regression

2 結果

2.1 摩擦力

本研究對6組托槽-弓絲組合進行了不同傾斜角θ下的摩擦力測試，見圖4、表1。各組數據均遵循同樣的趨勢，即首先摩擦力值保持平穩，隨角度的增加變化不大，而在特定的角度 （臨界角） 之后隨角度的增加出現上升，并基本保持線性上升。各組托槽與弓絲間的摩擦力值不相同，臨界角的大小也有所差異。

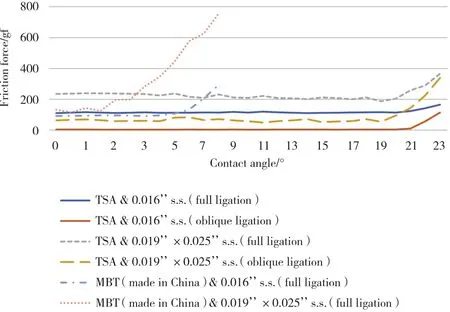
圖4 不同“托槽-弓絲”組合的摩擦力圖Fig.4 Friction force （gf） of combinations of brackets and archwire

表1 不同“托槽-弓絲”組合的摩擦力值 （gf）Tab.1 Friction force of combinations of brackets and archwire （gf）

（續表）

表2 不同“托槽-弓絲”組合的臨界角計算Tab.2 Contact angle of different combination of brackets and archwire

2.2 臨界角

利用二階多項式回歸法，得出不同“托槽-弓絲”組合的回歸方程和線性方程，并計算出臨界角值θ c，見表2。

3 討論

在使用方托槽正畸治療的過程中，牙齒不斷發生著“傾斜-直立-傾斜-直立”的復雜變化［4］，托槽槽溝表面及托槽翼內壁不可避免地要與弓絲相接觸，互相間便隨之產生了摩擦力。托槽與弓絲之間的摩擦力貫穿于整個正畸治療的過程。

臨界角 （θ c） 的概念由KUSY等［2］于1997年提出，是牙齒發生傾斜至弓絲剛剛開始同時接觸槽溝齦牙合兩端時，托槽槽溝與弓絲之間的角度，是托槽與弓絲處于被動狀態和主動狀態交界點處的傾斜成角。正畸中的滑動摩擦力包括經典摩擦力、約束摩擦力和刻痕阻力3部分。托槽與弓絲間的摩擦力組成隨兩者相互狀態的不同而變化：當托槽與弓絲之間的傾斜角小于臨界角時，托槽與弓絲處于被動狀態范圍之內，滑動摩擦力僅為經典摩擦力，不隨傾斜角的變化而變化；當傾斜角大于臨界角時，托槽與弓絲處于主動狀態范圍之內，在弓絲沒有到達刻痕狀態之前［5］，滑動摩擦力等于FR與BI之和 （FR+BI） ，隨傾斜角的增加呈線性增大［6］；在弓絲到達了刻痕狀態之后，滑動摩擦力等于FR、BI、刻痕阻力之和（FR+BI+NO）［2-3］，這種情況不在正畸學研究范疇之內。

本研究結果提示，托槽與弓絲之間的摩擦力臨界角大小與托槽的設計密切相關，傳動直絲弓的尖牙托槽的臨界角在18.79°～20.94°之間，MBT直絲弓托槽的臨界角僅僅在2.23°～4.55°之間。可見傳動直絲弓的尖牙托槽的臨界角值顯著大于MBT托槽。因此，傳動直絲弓托槽在臨床上允許尖牙發生更大范圍的傾斜，利于牙齒移動，無論是對于不拔牙病例的牙齒排齊，還是對于拔牙病例的近遠中向移動牙齒關閉間隙，都有積極的作用［7-9］。傳動直絲弓矯治器及矯治技術，是林久祥教授經過10余年的研究與實踐，探索研發出的具有自主知識產權的新一代低摩擦力直絲弓矯治器及矯治技術［10］。該矯治器的核心之處是尖牙托槽，吸納了自鎖托槽和Tip-Edge Plus托槽的優點。本研究顯示傳動直絲弓尖牙托槽具有如下特點：通過不同的結扎方式，與不同尺寸的弓絲組合，既能提供較小的摩擦力，又能提供較大的摩擦力。如圖2所示，傳動直絲弓托槽與0.016’’不銹鋼圓絲斜結扎，其摩擦力值最小，幾乎可以達到自鎖托槽的效果［11-12］；而傳動直絲弓托槽與0.019’’×0.025’’不銹鋼方絲全結扎時摩擦力較大，其被動范圍內的摩擦力值最大。傳動直絲弓托槽能夠達到自鎖托槽的“自鎖”效果，主要是因為傳動直絲弓托槽的設計者在近遠中托槽翼之間增加了臺階 （圖1） ，因此在對弓絲進行斜結扎時，該“臺階”結構使結扎圈 （或結扎絲） 與弓絲不接觸或者少接觸，大大減小了弓絲受到的結扎力，從而減少了托槽與弓絲之間的摩擦力。

該矯治器及矯治技術于2006年在第二屆海峽兩岸四地口腔正畸學術大會上公布，引起熱烈反響，標志著我國正畸領域不是僅僅停留在引進、學習國外先進技術的水平，而是能夠通過總結、比較、研究、實踐進行自主創新，進入了一個新的階段［13-15］。林久祥教授在研制矯治系統的同時，提出了“傳動力及傳動效應”的理論機制，在臨床中實現輕力矯治，因此僅依靠簡單的口內支抗基本滿足臨床需要。目前，第三代傳動直絲弓矯治器正在研發之中，試圖通過改進尖牙托槽的結構，進一步加大尖牙托槽的臨界角［13］。本研究的結果將為傳動直絲弓的臨床應用及進一步研發提供實驗依據。

臨界角的實驗值并非通過測試直接得出，而是依據測試出的摩擦力值，經過統計分析計算得來。不同的統計方法、不同的計算方法會導致臨界角實驗值不同。目前有關臨界角體外實驗的報道僅限于國外的KUSY等［16］和國內的LIU等［1］、丁鵬等［11］，他們使用的都是理論臨界值參考回歸法，其方法是以臨界角的理論計算值［6］作為被動范圍和主動范圍回歸分析的分界點，分別求得回歸方程后取交點，交點處的傾斜角即為臨界角的實驗值。這種統計方法相對簡單，結論較為可靠。但是需要指出的是，理論臨界值參考回歸法預先設定了2個回歸方程的范圍，最終的回歸結果在一定程度上依賴于理論臨界角的數值，而非完全依據實驗測量出的摩擦力觀測值，因此，該統計方法仍存在一定的局限性。

本研究應用的二階多項式回歸法是首次提出并探索性應用于臨界角計算的統計方法。這一大膽的嘗試基于KUSY等［16］的研究，該研究發現二階多項式的曲線能夠很好地擬合各個傾斜角度下的實驗觀測值，但并未進一步應用二階多項式計算臨界角。本研究以這一發現為基礎，嘗試通過建立二階多項式模型，計算臨界角的數值，其優勢在于數據的統計過程脫離了對理論值的依賴，完全依據實驗測量出的摩擦力觀測值。

在托槽相同的條件下，弓絲尺寸越大，臨界角越小。在弓絲相同的條件下，托槽槽溝的設計對臨界角大小的影響非常顯著，如傳動直絲弓托槽的臨界角遠大于MBT直絲弓托槽的臨界角。

當托槽-弓絲之間傾斜角小于臨界角時，摩擦力變化不大，不隨傾斜角的變化而變化；當托槽—弓絲之間傾斜角大于臨界角時，摩擦力隨傾斜角的增大呈線性增加。

傳動直絲弓托槽能夠通過全結扎和斜結扎2種結扎方式，提供較大或較小的摩擦力，其獨特的設計能夠增大臨界角，增加托槽與弓絲的被動范圍，允許牙齒在移動過程中發生更大的傾斜。