利用月掩星現象測量月球公轉周期
李壯壯,崔士舉
(東北師范大學 物理學院, 吉林 長春 130024)
月亮在天空自西向東移動,有時候會把天上的星星遮蔽起來,這種現象叫做“月掩星”[1]. 觀測月掩星能幫助我們研究月亮上有無大氣,利用月掩星光電觀測還可以測定恒星的角直徑[2]、多顆恒星的分離[3]及測量地球自轉的長期變化[4]等. 所以世界各國天文臺都很重視觀測月掩星的現象[1].
在月掩星現象即將開始階段(可以不考慮邊緣衍射[5]),通過觀測月球相對遙遠恒星的相對視角隨時間的變化,加上地球自轉的影響,結合電腦軟件處理,在短時間內得到月球公轉周期. 由于時間短,現象普遍,該實驗可以用作科普實驗,也可用作培養學生興趣和動手能力的教學實驗. 長期觀測,則可以研究月球公轉角速率的變化.
1 實驗研究
該實驗進行了2次觀測,第1次在2018年3月25日19:10,第2次在2018年7月23日21:00,2次均在東北師范大學物理學院天文臺觀測.
1.1 實驗儀器
實驗使用了Sky-Watcher 150PDS望遠鏡(D=150 mm,F=750 mm)[圖1(a)],ZWO ASI120MC攝像頭[圖1(b)示]、數據線、雙軸電跟、聯想牌筆記本電腦.

(a)望遠鏡

(b)攝像頭圖1 實驗儀器
1.2 實驗觀測
1.2.1 實驗現象
圖2是第1次觀測的圖片,圖3是第2次觀測的圖片,箭頭指向恒星. 由于拍攝的照片不易觀測,圖2~3均使用了Photoshop cs8.01軟件進行反相,調節對比度為40%,亮度為40%,及調節色階處理,最后對星點進行了顏色加深處理.

(a)開始觀測時

(b)大約6 min后圖2 第1次觀測
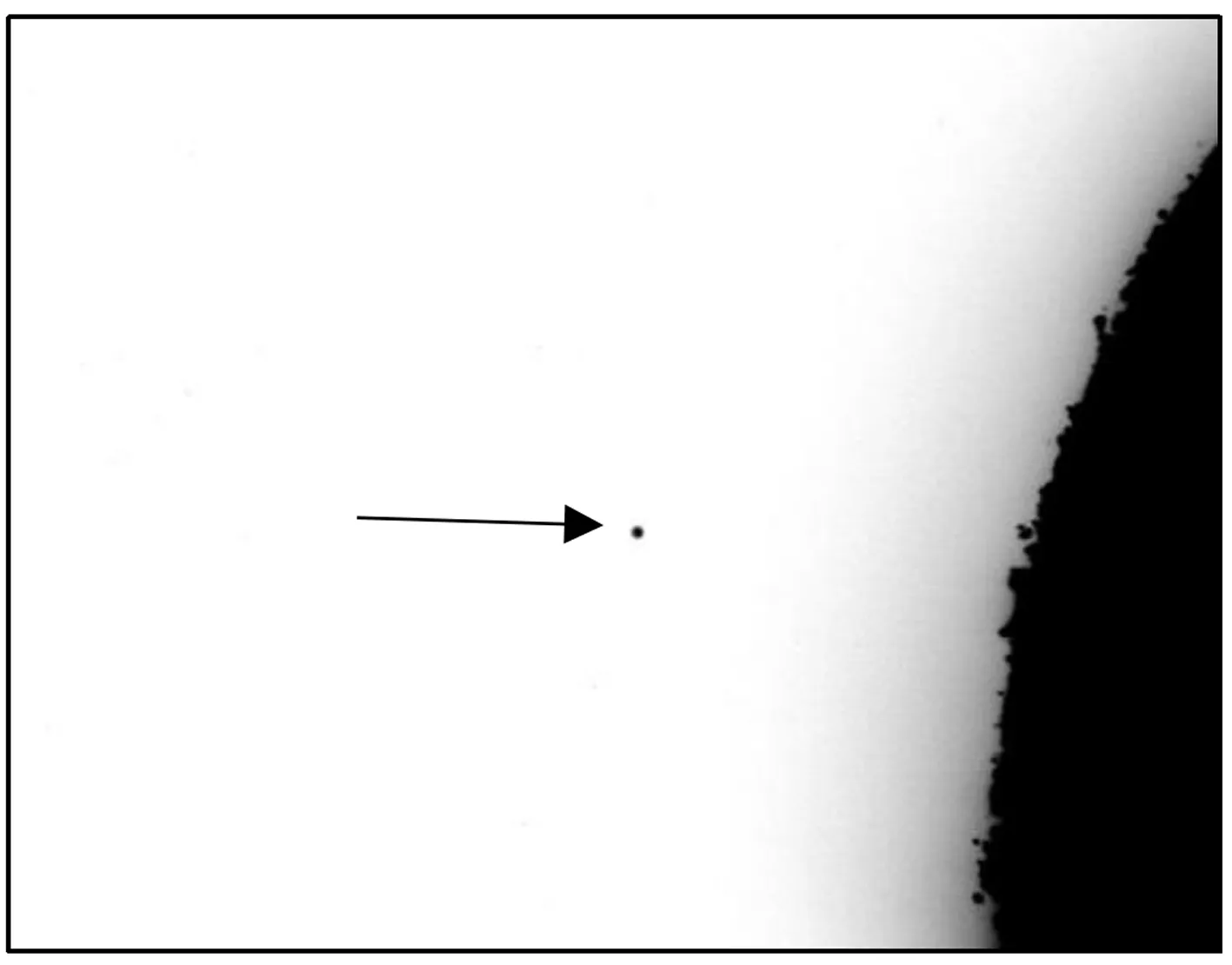
(a)開始觀測時

(b)大約6 min后圖3 第2次觀測
1.2.2 數據測量及處理
月球公轉軌道參量和物理參量如下[6]:近地點距離362 570 km,遠地點距離405 410 km,半長軸s為384 399 km(本文以半長軸為月球軌道半徑計算),軌道周期為27.321 582 d,平均半徑1 737.10 km,質量7.347 7×1022kg. 2次觀測處理方法相似,以第1次處理方法為例.
1)定標
將視頻中的某一幀圖片提取出來并保存為圖片格式(此次提取最后一幀),用Photoshop調整亮度和對比度并進行usm銳化處理,使之更清晰,再將此圖片導入到迅捷CAD編輯器,利用該軟件作圖和測量的功能進行定標,步驟為:
a. 在圖片上顯示的部分月面的邊緣部分標記3個點,并用線段連接相鄰的2個點;
b. 畫出這2條線段的中垂線,2條中垂線的交點即為月球在此平面投影出的圓的圓心;
c. 利用該軟件的測量功能,測量圓面的邊緣到圓心的距離,得到1個數值,在測量數據窗口設置尺寸中填入月球平均半徑,會自動生成相應的比例;
d. 在該比例下,測量出此圖像畫面的長,得到的數據記錄下來,定標結束. 如圖4(a)所示.
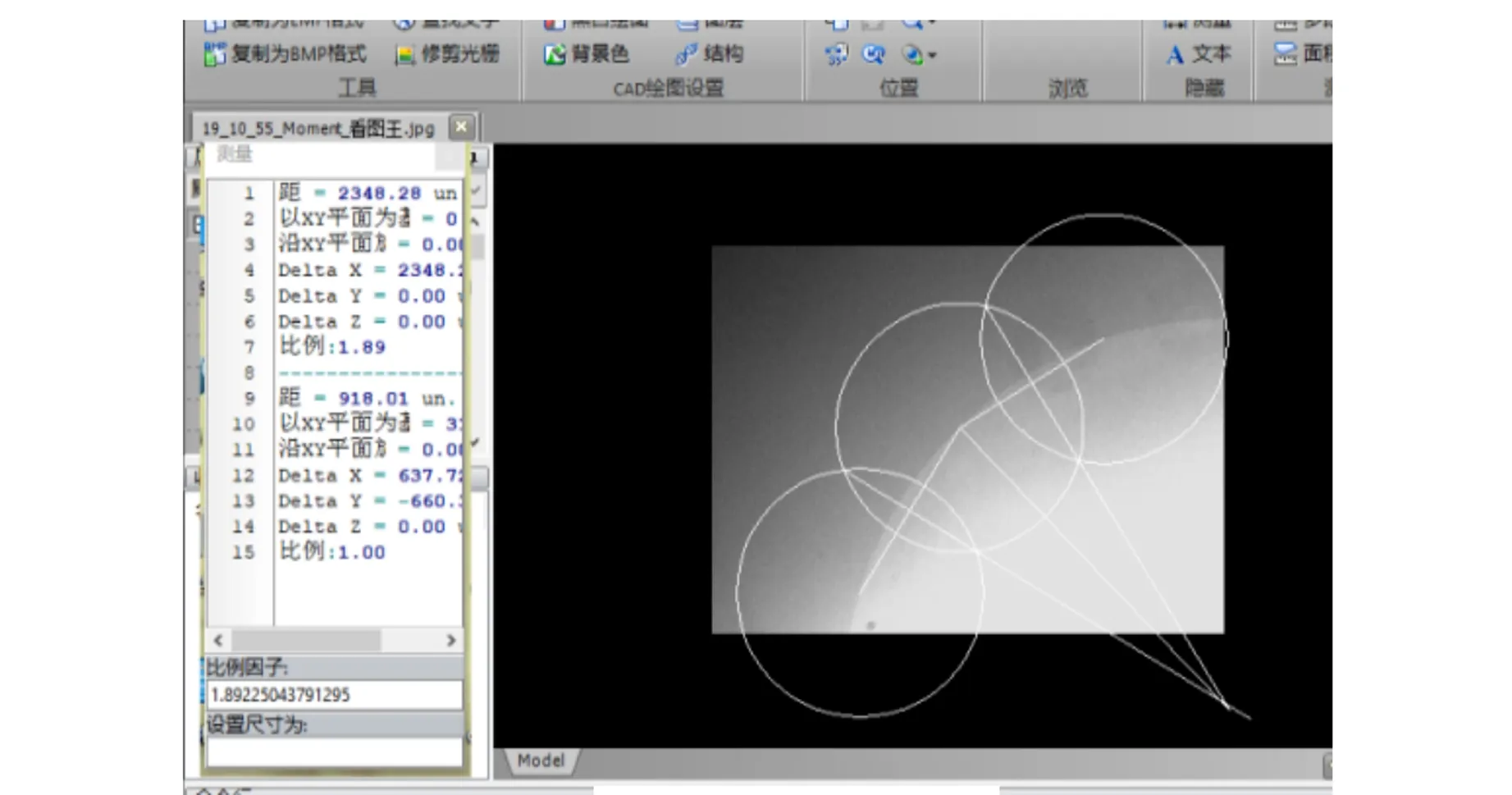
(a)定標
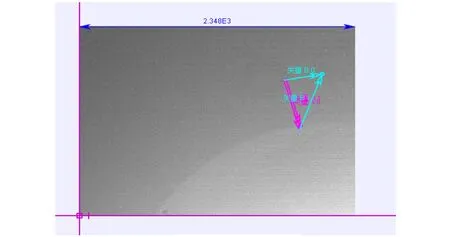
(b)建立坐標圖4 定標建系
2)跟蹤測量
打開Tracker軟件,將完整視頻導入,利用Tracker軟件進行月球和恒星相對位置的跟蹤和測量,步驟為:
a.建立坐標軸,選圖片左下角作為直角坐標系的原點如圖4(b)所示;
b.建立定標尺,將定標尺與視頻畫面的長重合,將用CAD編輯器測出的定標數據填入,回車鍵確認;
c.建立矢量B,將視頻調到第1幀,記下月球某點在圖中位置及恒星在圖中位置,之后找到月球恰好要遮到恒星的那幀圖像,設置視頻只播放到此位置,并記錄此時恒星和月球某點(遮到恒星處)相對于圖像的位置;
d.利用矢量B畫出恒星相對圖像(建立的坐標系)的位矢B0,月球相對圖像的位矢B1,找到月球相對于恒星的相對位矢B2,如圖5所示;
e.建立矢量A,設置視頻每次間隔10幀顯示1次畫面,將每次畫面中的月球某固定點(月球遮到恒星的點)與恒星點用矢量A連接,并保持矢量Ai平行于位矢B1,畫出若干位矢,即A1,A2,A3…,如圖5所示;
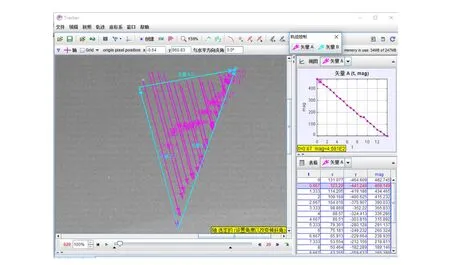
圖5 跟蹤測量
f.將測量的數據導入Excel表格,并將幀數換成對應時間,在Origin軟件中畫出位矢A的長度隨時間的變化曲線,即月球相對于恒星的距離在月球公轉軌道切面(月球直徑遠小于地月距離,近似認為在公轉軌道切面上)的投影長度隨時間的變化曲線,如圖6所示;
g.利用線性擬合得到月球相對恒星在運行軌道切面投影的速度,通過近似計算得到月球公轉軌道周期. 根據圖6所示線性擬合方程
l=-0.700 5t+460.5 ,
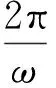
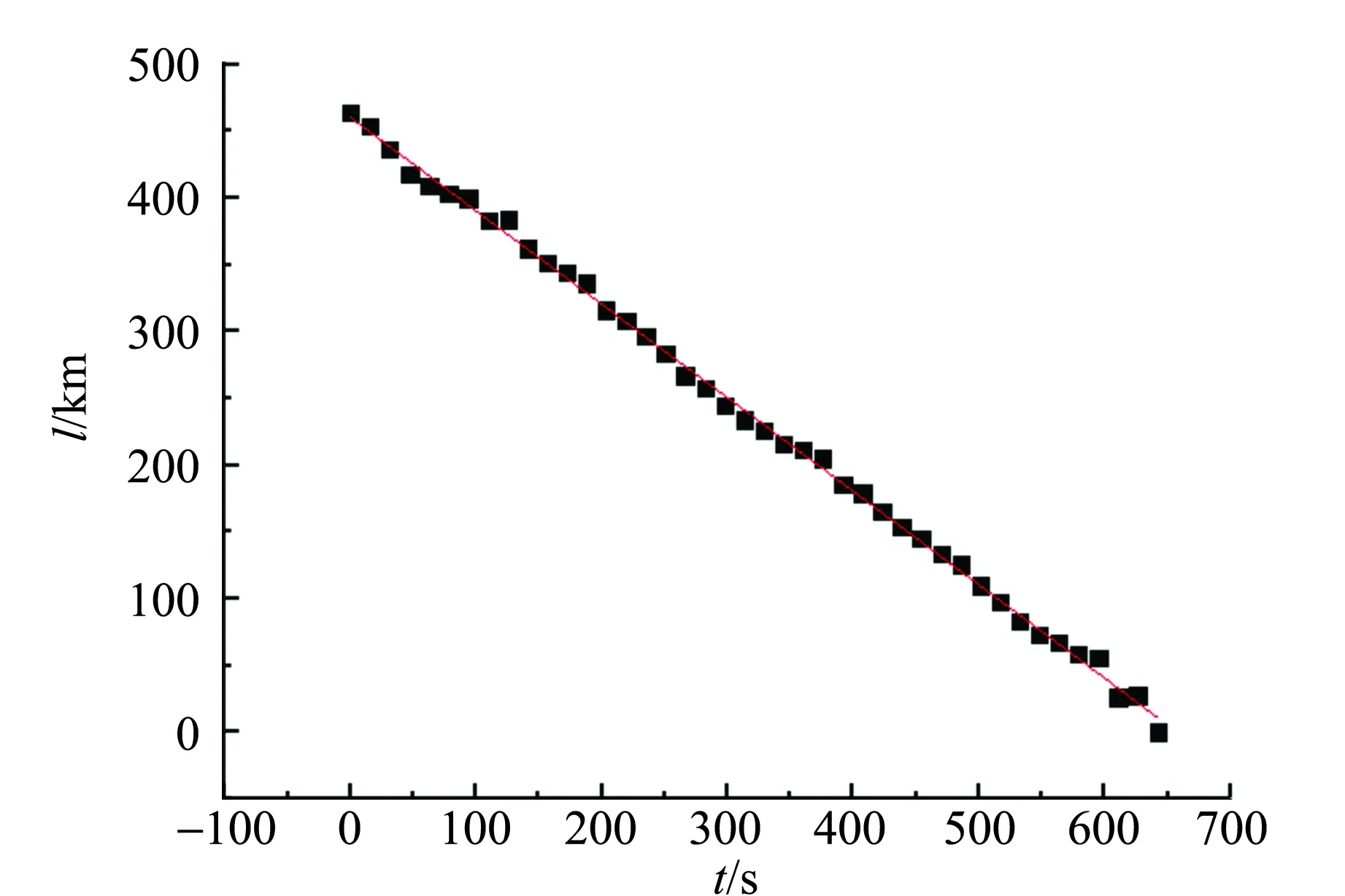
圖6 月球和恒星平面投影相對距離l隨時間t變化
2 理論修正
2.1 恒星認為不動的解釋
第1次拍攝時間在2018年3月25日 19:10分,通過Star Walk確定視頻中的移動的亮點為HIP 34243星,距離太陽的平均距離為3 545.254 ly,并假設此星移動速度為光速(實際遠小于光速),觀測時間約為642 s,則移動視角為β=5.742×10-9rad,遠小于10-6量級,而恒星運動速率實際是遠遠小于光速的,故更可以認為恒星是靜止不動的.
2.2 修正地球自轉影響
以上計算結果和實際月球軌道周期對比相差很大,主要原因是地球自轉的影響,對于月球自轉,由于自轉周期和地球基本同步,在較短的時間內其影響可忽略不計. 如圖7所示,其中r是圖8中的r,不是地球半徑;對于圖8,開始觀測時觀測者在C位置,一段時間后,到D位置,月球從藍色位置到白色位置,其中是CE長度,近似等于地月距離s(r?s,故r+d≈d≈s),而地球自轉產生的影響主要在于CD,故可以簡化模型,變成如圖7所示,其中h為觀測者認為月球移動的距離,h+x為月球實際運動的距離,s為地月距離,r為如圖2中r,θ為觀測時間內地球轉過的角度(很小),l為恒星距離地球的距離(l?s),α為觀察者的地理緯度.
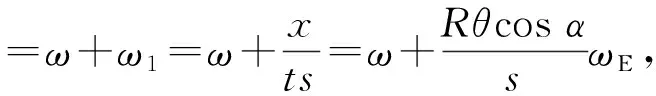
其中地球自轉角速度為
月球繞地公轉半長軸為[6]:
s=384 399 km.
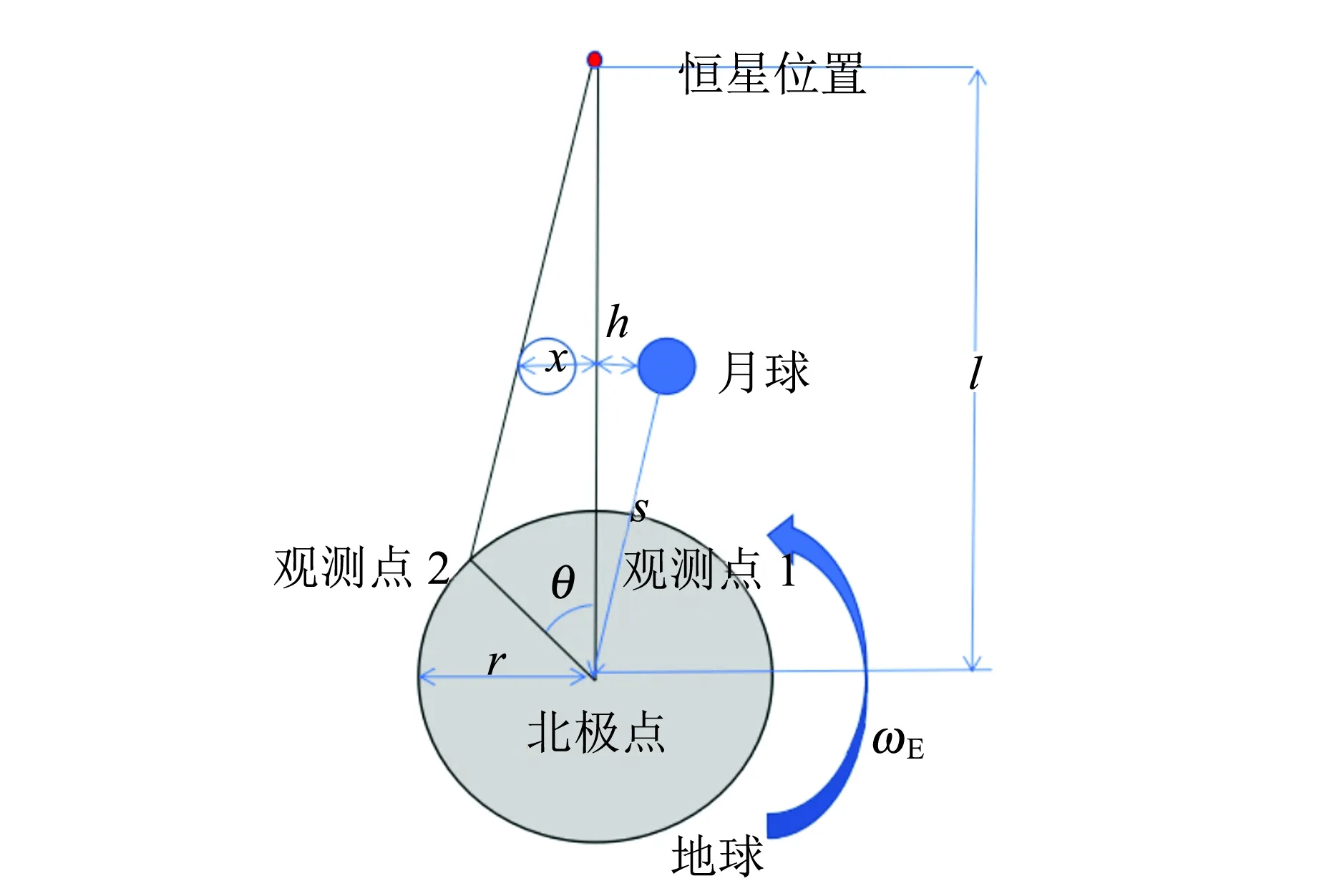
圖7 簡化模型
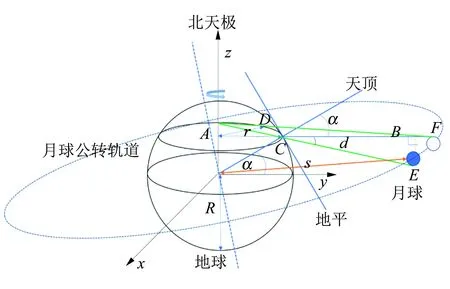
圖8 三維模型
在計算中可以簡單地把地球作為圓球,半徑約為[7]R=6 371 km,觀測地的緯度α=43°51′,則
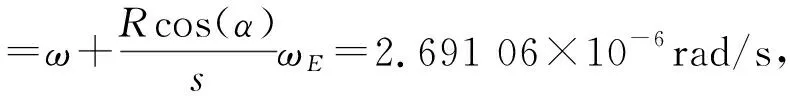
算得周期為
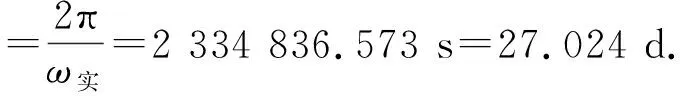
與實際軌道周期:27.322 d相差少于1 d,相對偏差為η=1.09%. 可見此方法還是可行的.
圖9為第2次測量的數據處理,同上的處理方法及加上地球的自轉的影響,使用Star Walk軟件確定第2次觀測對應的亮星為HIP82465星,到太陽的平均距離為982.42 ly,也遠遠大于地月距離,在短時間觀測可以近似認為亮星位置保持不變. 最終求得3次計算的公轉周期分別為:27.351 d,27.205 d,27.091 d,平均約為27.216 d,接近實際運行周期27.322 d.
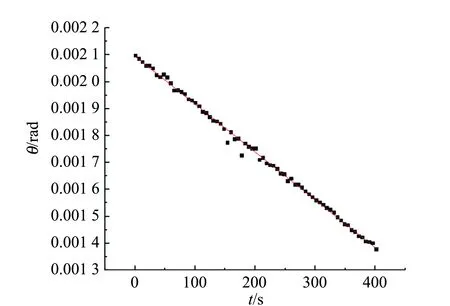
(a)星月地夾角θ隨時間t變化
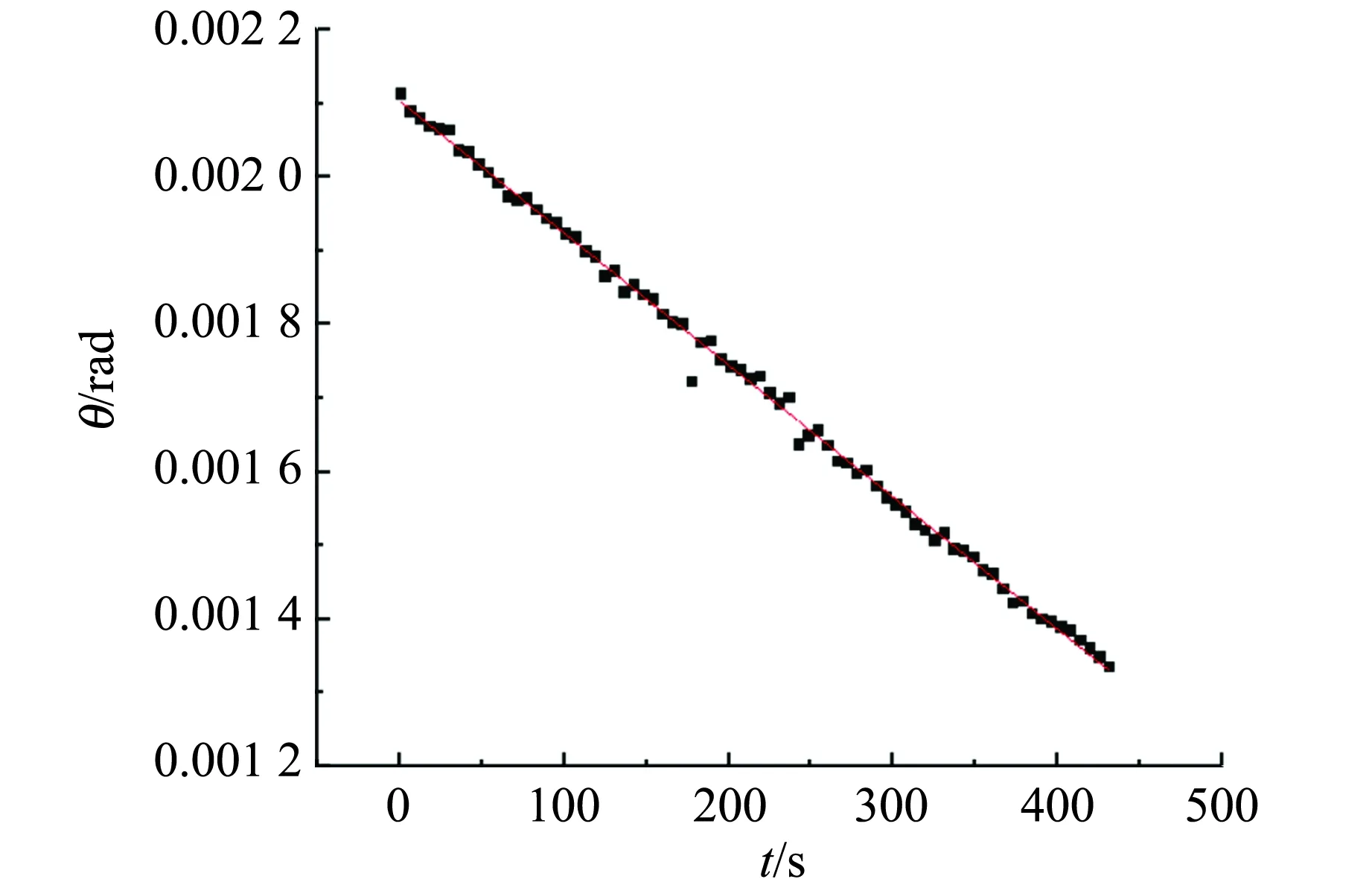
(b)星月地夾角θ隨時間t變化
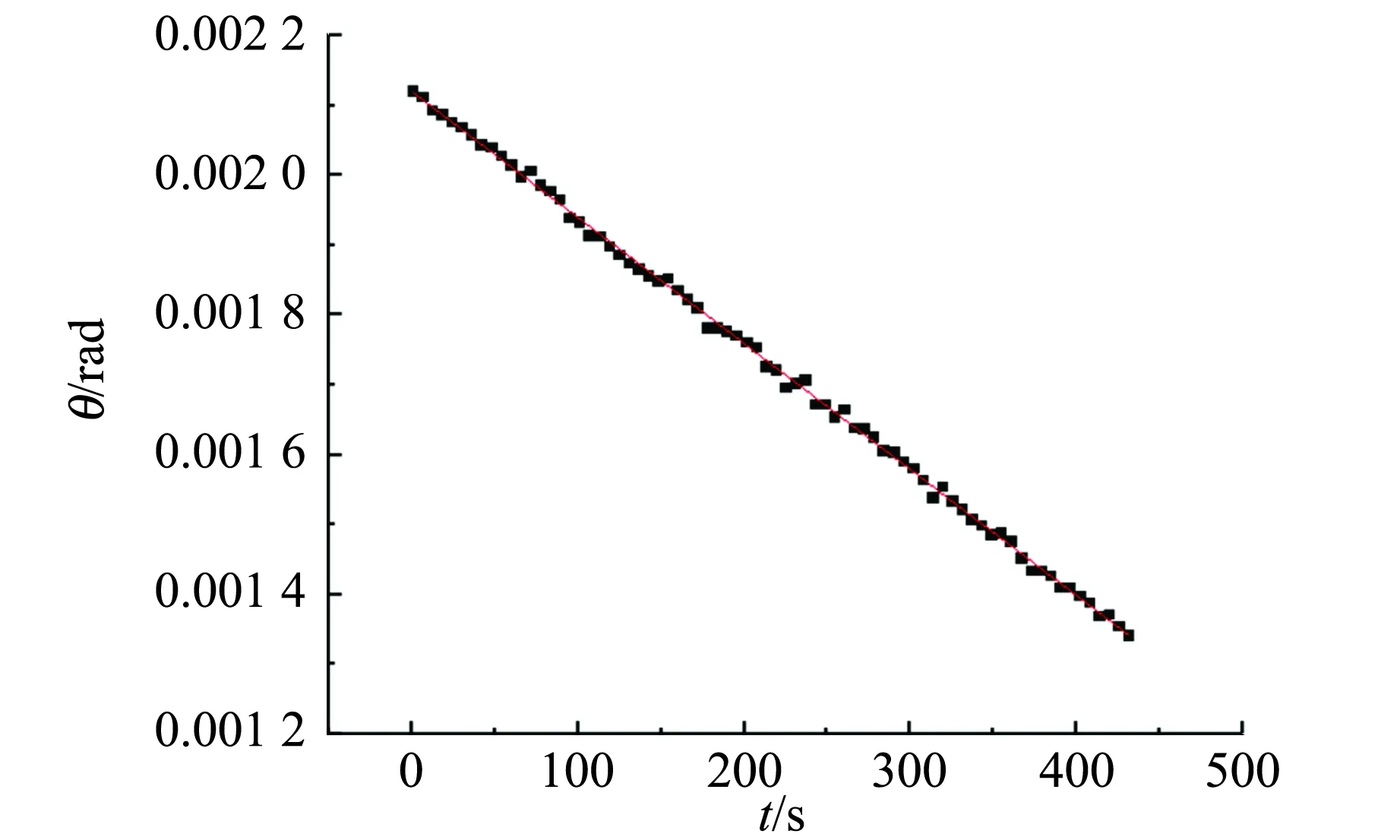
(c)星月地夾角θ隨時間t變化圖9 第2次觀測結果
3 誤差來源及分析
誤差產生來源于主要有:
1)實際軌道為橢圓軌道,而本實驗近似為簡單的圓軌道;
2)跟蹤月球和恒星距離變化過程中不能完全跟準在月球上的固定點,采用多次跟蹤測量求平均值(如第2次觀測處理),但還會存在誤差;
3)修正地球自轉影響時為方便采用了近似.
以第1次觀測為例,由于月球繞地球運動是橢圓軌道,而本文按圓形軌道計算,實際月球繞地球公轉時會有近地點和遠地點,在不同的位置月球公轉的線速度是不同的,而這里采用的方法測得的是觀測時間內的月球平均公轉線速度,相對于月球運轉軌道周期來說可以認為是瞬時速度大小,此速度應該是在近地點和遠地點速度大小之間,通過以上觀測和計算得到第一次觀測時月球在該時間內的平均公轉線速度大小為
v=ω實s=1 036.17 m/s.
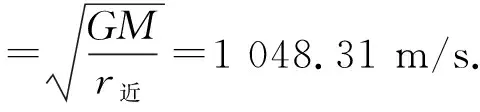
月球在遠地點的瞬時速度大小為
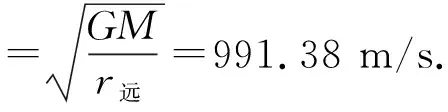
可見實際觀察的瞬時速度大小在其范圍內,可認為是可行的.
4 結果與討論
通過以上的處理和計算可以發現用月掩星現象測量月球公轉周期的方法是可行的,由于月掩星現象相比于月食現象更普遍,而且觀測時間較短,使用儀器簡單. 雖然會產生一定誤差,但用于天文學教學、科普教學還是可行的. 改進更精準的方法和應用更全面的理論則可以用于科學研究,長期觀測以考察地球自轉和月球公轉的變化[4]等都具有實際意義.

