基于菲涅耳原理的小孔衍射
胡志剛,李佳迅,蘇開齊,胡清雨,朱昨磊,鄭琳麗,鄧邦林
(成都理工大學 地球物理學院,四川 成都 610059)
2018年國際青年物理學家錦標賽(IYPT)和2018年中國大學生物理學術競賽(CUPT)中有題目為“Radiant lantern”(燈光四射),描述了以下問題:在晚上給點燃的提燈拍照,會有大量從提燈中心發出的光線顯示在照片上. 試解釋并探究這一現象. 在運用相機拍攝點亮的提燈時,得到了相應的射線的現象. 光線在經過相機鏡頭時,傳播方向發生偏離,這種光線偏離初始傳播方向的現象與光學中的衍射現象[1]是相同的. 本文從衍射的角度出發,引入光的衍射公式,嘗試解釋照片中點亮的提燈中心發出大量射線的原因,并通過Mathematica計算仿真[2],探究相關物理量對實驗現象的影響,并設計實驗定性驗證仿真結果.
1 理論分析與模擬仿真
1.1 射線現象成因
單反相機成像示意圖[3]如圖1所示. 外部景物的光線依次通過鏡頭組、光圈、反光鏡,最后通過五棱鏡的2次反射穿過取景器. 拍攝時按下快門鍵,反射鏡抬起,光圈預縮到設定的大小和形狀,光線入射到膠片上. 光線在經過照相機后發生了衍射,實際過程對應著按下快門,光圈縮小,光在經過較小的障礙物光圈后發生了衍射.
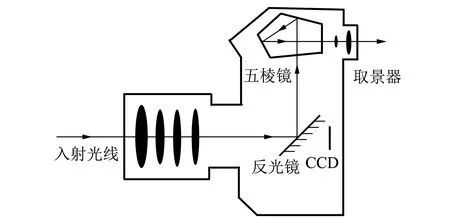
圖1 單反照相機成像示意圖
照相機的簡化光路如圖2所示,惠更斯-菲涅耳原理[1]為
(1)
其中,C為比例系數;K(θ)為傾斜因子,其值隨著θ增大而減小;A(Q)為分布函數,即光強振幅通過光圈以后在Σ小孔上的分布;r為光圈上的點到屏衍射點的距離,k為波數.
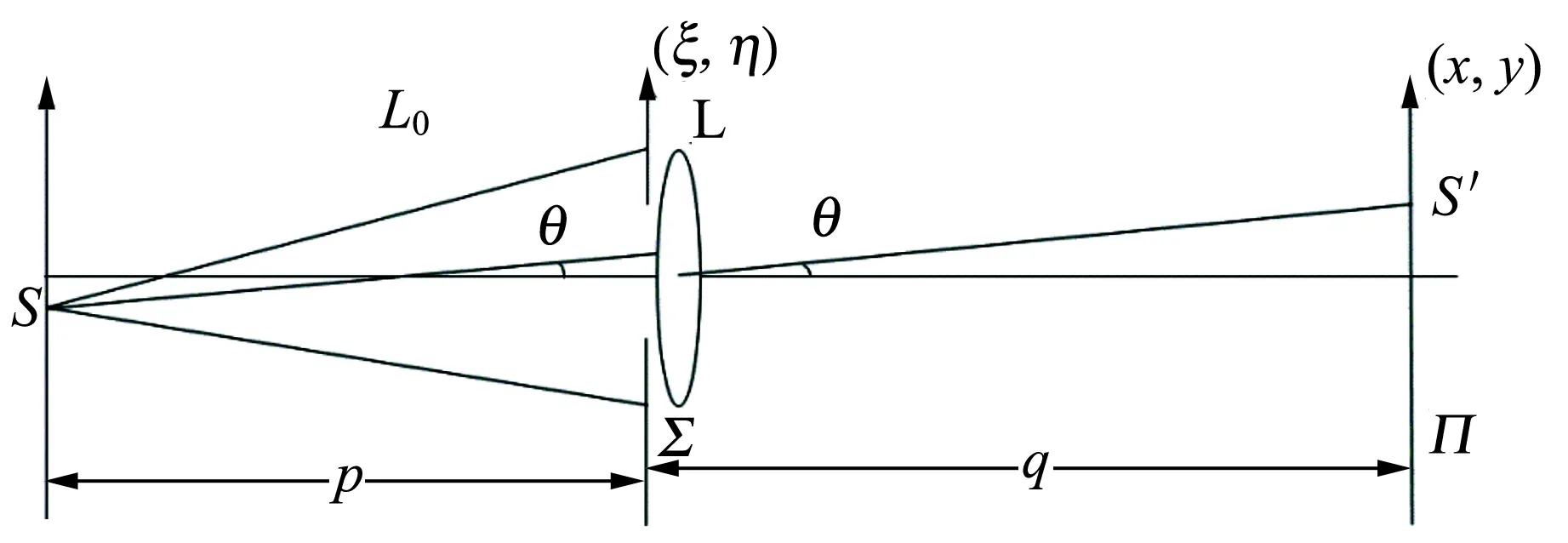
圖2 照相機簡化光路圖
運用格林公式求解出基爾霍夫衍射公式,對比例系數和傾斜因子[4]描述為
(2)
A(ξ,η)=B(ξ,η)T(ξ,η).
(3)
(3)式表示光強振幅在通過光圈以后的分布,B(ξ,η)為光強振幅在透過光圈以前在孔上的分布情況,T(ξ,η)為光圈的透射系數,如果是空氣,此時值為1.
相機中的膠片是個很小的區域,近似認為θ不變,傾斜因子是定值,即為1,(2)式簡化得到
(4)
根據波動光學[5],薄透鏡是相位變化元件,相位變化因子表達式為
(5)
式中EL0是透過透鏡的光強復振幅.
考慮衍射和相位變化后,透過光圈的光強振幅分布為
A(ξ,η)=B(ξ,η)T(ξ,η)TL(ξ,η).
(6)
根據傅里葉光學[6],點光源發出的光線的光強振幅在光圈上的分布函數為
(7)
(4)式中r是光圈上點到衍射屏上點的距離,為
(8)
將(8)式二項式展開,并忽略高階小量,將得到結果和(6)式代入(4)式,得:
(9)
根據高斯公式,
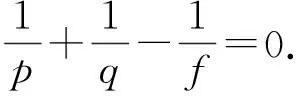
為了更好地描述各點衍射強度的關系,計算衍射光照強度的大小. 光照強度的計算公式為L=|E|2,由于
故光照強度為
(10)
1.2 數值模擬
用Mathematica計算上述方程,并對計算結果可視化. 計算過程中,取光的波長為500 nm,定義r0為孔徑,即是孔的幾何中心到孔的頂點的距離,且計算過程中孔為正多邊形.
1.2.1 孔的形狀的數值模擬
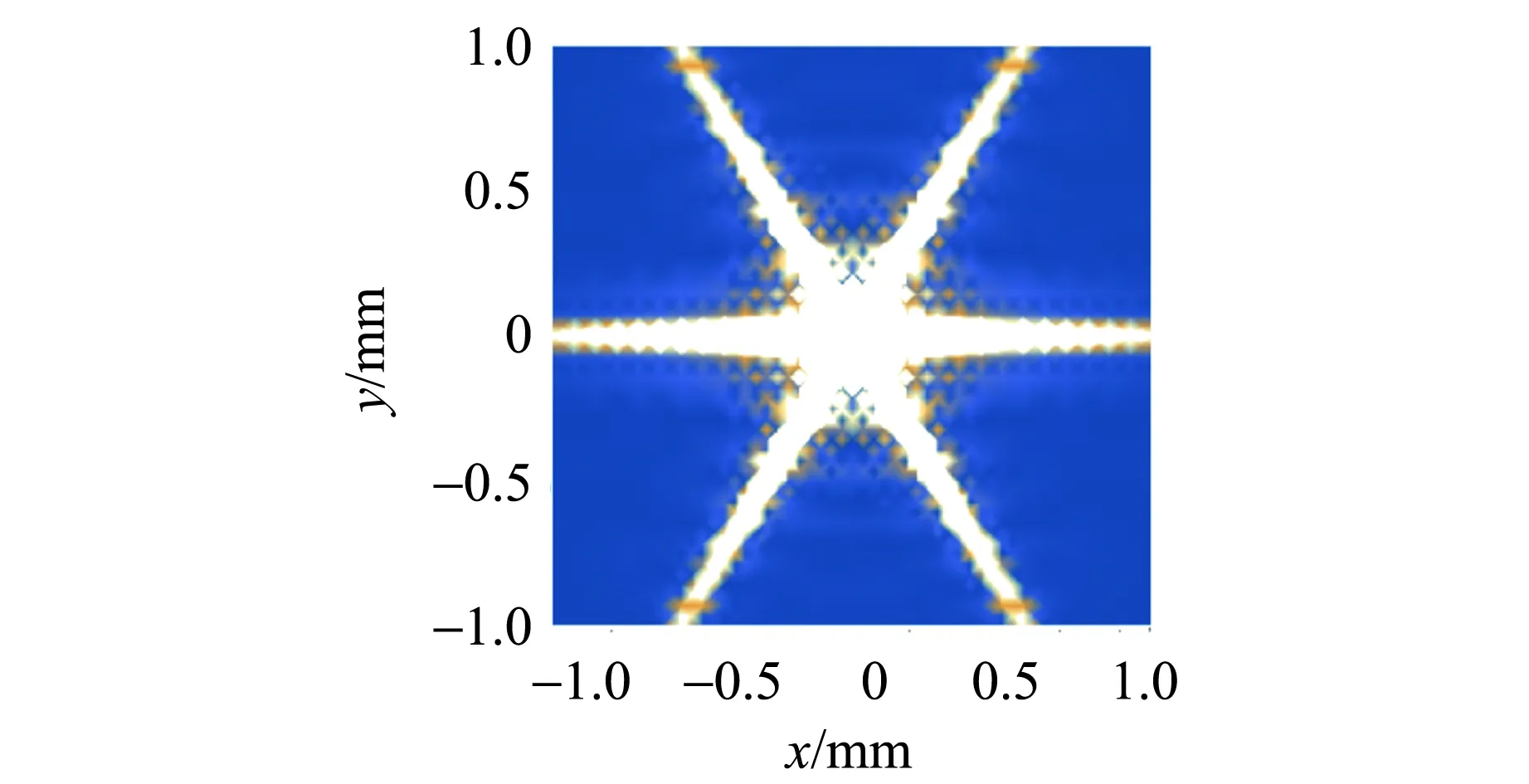
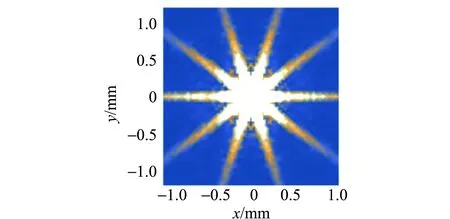
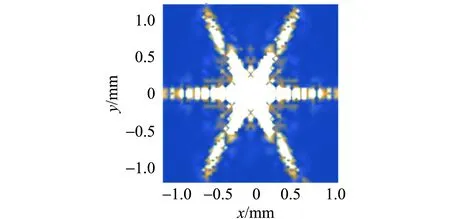
首先對不同形狀的孔[7-8]進行模擬計算,得到部分衍射的理論圖樣如圖3所示.λ=500 nm,r0=0.5 mm,q=0.1 m. 從仿真結果可以看到衍射射線數目呈現的規律為:當孔的邊數為奇數時,射線數目為邊數的2倍;當孔的邊數為偶數時,射線數目與邊數一致. 對衍射射線數目的定性解釋:光在經過孔的過程中,孔的每條邊都會發生衍射,每條邊都會衍射出2條方向相反的射線條紋,當孔的邊數為奇數時,任意2條邊都是交錯的,所以得到的衍射射線條紋方向也一定是交錯著的,即不會存在完全重合在一起的2條條紋,所以衍射射線條紋數目是孔邊數的2倍. 當孔的邊數為偶數時,由于存在對邊相互平行,這2條平行邊的衍射結果也重合,所以最終在衍射屏上得到的射線數目也和孔的邊數一致.
(a)三角形
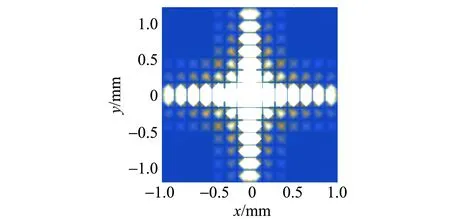
(b)四邊形
(c)五邊形
(d)六邊形
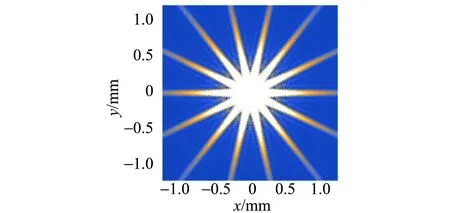
(e)七邊形圖3 不同形狀孔的計算結果
1.2.2 孔徑的數值模擬
用Mathmatica計算七邊形孔的孔徑,λ與q控制不變,仿真結果如圖4所示. 其中I為x軸方向的衍射強度,I0為中央零級亮紋的衍射強度[9-10]. 可見隨著孔徑不斷增大,各級亮紋的寬度變窄,這意味衍射減弱,說明實驗中改變光圈大小,照片上的提燈中心發出的射線強度發生變化.
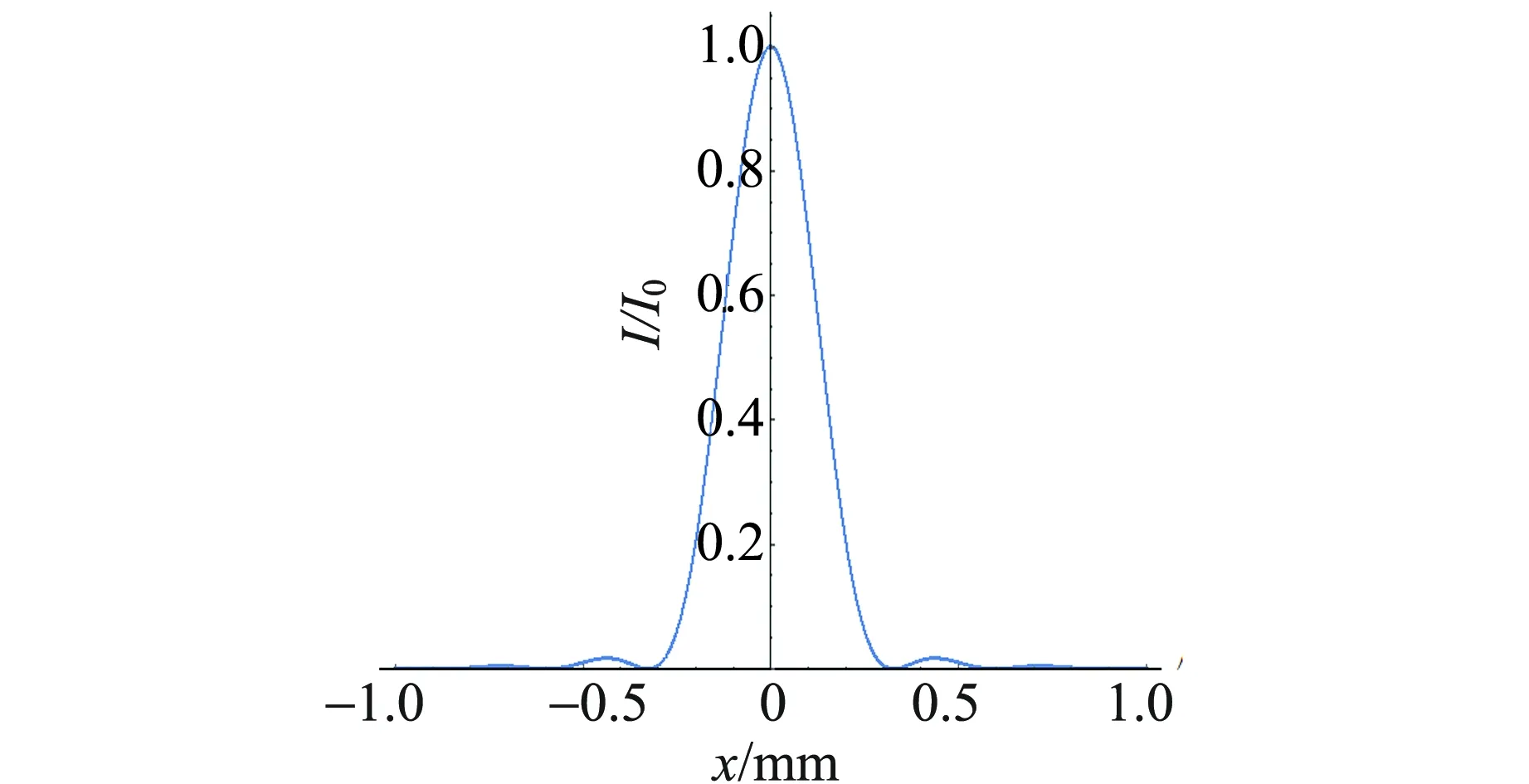
(a)r0=0.1 mm
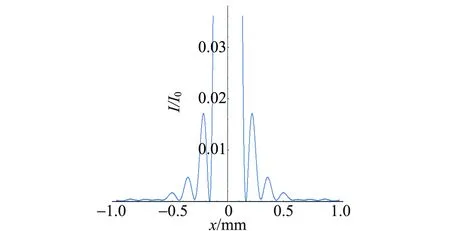
(b)r0=0.2 mm

(c)r0=0.3 mm
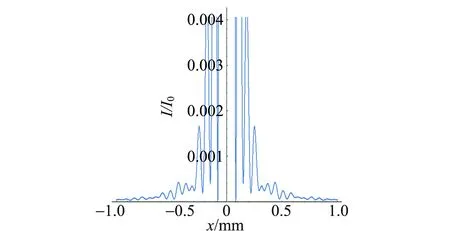
(d)r0=0.4 mm圖4 不同孔徑的計算結果
2 實驗研究
實驗裝置側視示意圖如5圖所示,相機型號為NIKON(D3200)的單反照相機(其光圈形狀為七邊形),光源用點亮的手機后置電筒替代提燈. 為了探究小孔形狀對射線形狀邊數的影響,準備了尼龍絲襪(拉伸仔細觀察,其形狀為三角形小孔),達到改變小孔形狀的目的.
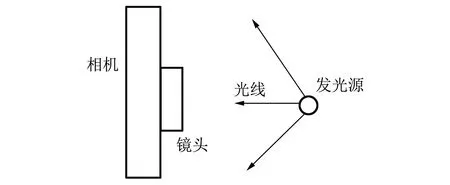
圖5 實驗裝置側視示意圖
圖6(a)是用尼龍絲襪小孔的實驗結果,可以看見照片上射線條紋數目是6條. 圖6(b)是對鏡頭不做處理得到的實驗結果,鏡頭的光圈形狀是七邊形,可以看見照片上的射線條紋數目是14條. 與理論分析中關于射線條紋數目的計算是吻合的,但是實驗中的現象與理論有差別,理論算出來的射線條紋隨著距離增加是越來越細的,而實驗結果中,射線條紋卻是越來越寬. 仔細觀察光圈的形狀,并且查閱相關資料,發現光圈的形狀并不是很規則的正多邊形,而是曲邊多邊形.

(a)尼龍絲襪小孔(三角形)

(b)光圈小孔(七邊形)圖6 尼龍絲襪小孔和鏡頭的光圈實驗結果
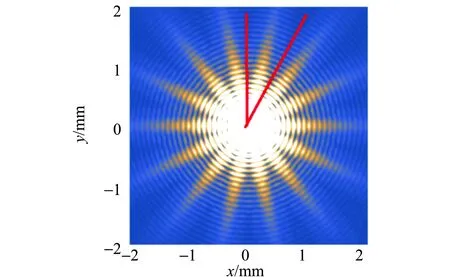
圖7 曲邊多邊形理論仿真圖
對更符合實際情況的光圈形狀進行模擬仿真,得到如圖7所示的仿真圖. 可以看到,光圈形狀設置成曲邊多邊形后,仿真結果和實驗結果[圖6(b)]吻合程度很好. 在衍射條紋條數的定性討論中,提到了衍射條紋方向與光圈的邊垂直,這解釋了實際實驗中的條紋會隨著距離的增加越來越寬:曲邊可以看成是很多短小直邊拼接而成的,每條直邊都會產生2條與之垂直的條紋,1條曲邊產生的條紋會呈現發散狀態,出現條紋越來越寬的情況.
3 結束語
從理論和實驗兩方面研究了2018年IYPT和CUPT賽題提到的燈光四射現象. 運用菲涅耳原理解釋了照片中提燈中心發出大量射線現象,對相機進行了模型簡化,由于光線在小孔處發生衍射從而產生了射線,運用衍射公式,對現象進行了數學描述. 對孔形狀與孔徑大小進行了模擬計算仿真,發現當孔的邊數是奇數時,衍射射線條紋數目是孔邊數的2倍;當孔的邊數是偶數時,衍射射線條紋數目與孔的邊數一致. 通過在鏡頭使用尼龍絲襪小孔及不對鏡頭做處理2組實驗,得到的衍射射線條紋數目實驗結果與仿真結果一致. 對孔徑大小做數值模擬仿真,發現隨著孔徑的增大,衍射光照強度減弱.

