關于旋度公式的推導方法

丁尚文 郭清偉 陳琳

摘 ?要 以水漩渦為例，討論漩渦中微元旋轉強度問題。采用環流量與面積之比的極限對水漩渦中心處的微元旋轉強度建立數學模型，通過數學模型求解找出速度場與旋度場之間的聯系，推導出旋度概念和定義。該教學設計以水漩渦為例，借助數學建模方法培養學生解決物理問題的能力。

關鍵詞 水漩渦;旋度;環流量;角速度;數學模型

中圖分類號：G642 ? ?文獻標識碼：B

文章編號：1671-489X（2019）18-0098-04

Derivation Method based on Curl Formula//DING Shangwen， GUO Qingwei， CHEN Lin

Abstract Taking the water vortex as an example， this paper discusses

the measurement of the rotation intensity of the micro element in the

vortex. By using the limit of the ratio of annular flow to area， a mathematical model is established to measure rotation intensity of

the micro element at the center of water vortex. By solving the mathematical model， the relation between the velocity field and the

rotation field is found out， and the concept and definition of the curl

is deduced. This instructional design takes water vortex as an exam-

ple， and helps students develop their ability to solve physical pro-blems by means of mathematical modeling.

Key words water vortex; curl; annular flow; angular velocity; mathematical model

1 引言

旋度是多元函數積分學中一個重要的概念，在流體動力學、流體運動學和空氣動力學等領域有著非常廣泛的應用[1]。高等數學相關教材已給出旋度的概念和定義，教材設計通常是先給出環流量的密度公式，然后由環流量密度公式推導出在某一點處的旋度[2]。

國內外學者就旋度概念的理解和公式推導做出很多研究。任京男等提出關于奇點的旋度算法[3]。黃輝等把散度和旋度這兩個反映不同物理特性的物理概念加以比較，設計并實踐了以散度和旋度為內容的研究型教學模式[4]。Schey等考慮矢量函數在一個小長方形上的環流量積分計算，研究結果發現，環流量比上小長方形的面積再求極限值，與旋度向量的一個分量表達式完全相同[5]。杜曉燕等把亥姆霍茲定理等知識點作為例題，幫助學生理解旋度概念和應用[6]。黃國良等從流速場角度出發，詳細地說明了矢量場旋度的物理意義[7]。李黎等研究結果表明，旋度在變形體的速度場中仍然存在矢量場的旋轉特性[8]。徐亮等采用旋度公式對旋轉沖擊射流傳熱特性開展研究，結果表明，內置螺旋桿產生的旋流在靶標面上具有均勻高效換熱性能[9]。

上述文獻研究主要工作在旋度定義的理解和相關例子的補充上。旋度概念的產生在教材中較少出現，以及如何根據實際問題推導出旋度公式，這些問題仍然需要進行進一步補充和推導證明。

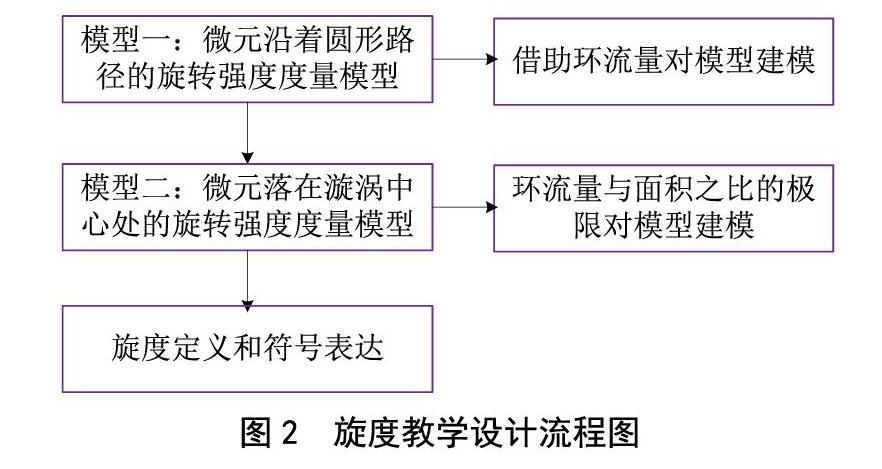
本文以物理現象水漩渦為例，闡述旋度概念的產生和公式的推導。旋度公式的推導首先從自然現象漩渦直觀認識出發，提出漩渦中某處微元的旋轉強度如何計算問題;其次，采用環流量與面積之比的極限對微元旋轉強度建立數學模型;最后，通過數學模型求解找出速度場與旋度場之間的聯系，推導出旋度公式。

2 漩渦中微元旋轉強度建模

背景 ?生活中遇到的漩渦例子很多，如水漩渦、風漩渦、飛機的尾部產生的氣流漩渦。漩渦的形狀如圖1所示。如何度量水漩渦旋轉強度？對此需要建立數學模型。為了分析簡單化和形象化，可以假設水漩渦某處有一個微元，該微元的旋轉強度與水漩渦的旋轉強度相同，度量水漩渦的旋轉強度間接轉化成度量微元的旋轉強度。

本文首先對漩渦中某微元在某處的旋轉強度建模。第一個數學模型是關于微元繞著圓形路徑旋轉一周的環流量的計算模型。該模型簡單、直觀，學生能夠想到用微元的環流量來度量水漩渦的旋轉強度。隨著問題的深入，如果漩渦中的微元循著螺旋路徑逐漸卷入漩渦中心，如何度量水漩渦中心位置處微元的旋轉強度？由此可以看出，該模型被用來度量微元在某一點處的旋轉強度顯然不準確。在此基礎上，采用環流量與面積之比的極限對微元旋轉強度建立數學模型，通過數學模型求解找出速度場與旋度場之間的聯系，給出旋度概念。本文建模設計具體流程如圖2所示。

問題分析 ?圖1中的漩渦在旋轉時與角速度有關，可以用右手法則確定角速度的方向，水漩渦的方向可規定與角速度的方向一致。假設水漩渦某處存在一個微元，該微元隨著漩渦在旋轉，微元沿著圓形路徑旋轉一周的環流量可以描述漩渦整體旋轉強度。微元沿著螺旋線型的路徑運動，微元逐漸被卷入水漩渦中心。微元在水漩渦中心處的旋轉強度不能夠單獨用環流量來描述和進行定量分析。如何解決微元在某一點處的旋轉強度？該類問題解決首先需要分析微元旋轉與哪些因素有關，具體見表1所示水漩渦旋轉強度相關變量表。

根據表1中的相關變量可以發現，微元在水漩渦中的旋轉強度與角速度、圓形半徑和環流量有關，水漩渦旋轉強度的方向可以規定與角速度的方向相同。

模型假設

1）研究水漩渦旋轉強度，假設一個微元處在漩渦中，該微元的旋轉強度與漩渦的旋轉強度一樣。

2）假設微元運動的角速度與漩渦旋轉的角速度大小相同。

3）為了簡化微元在水漩渦中運動的軌跡路線，微元在水漩渦中旋轉一周的軌跡路線為圓形路徑。

4）假設微元運動的線速度、角速度與微元在水漩渦中的位置有關。

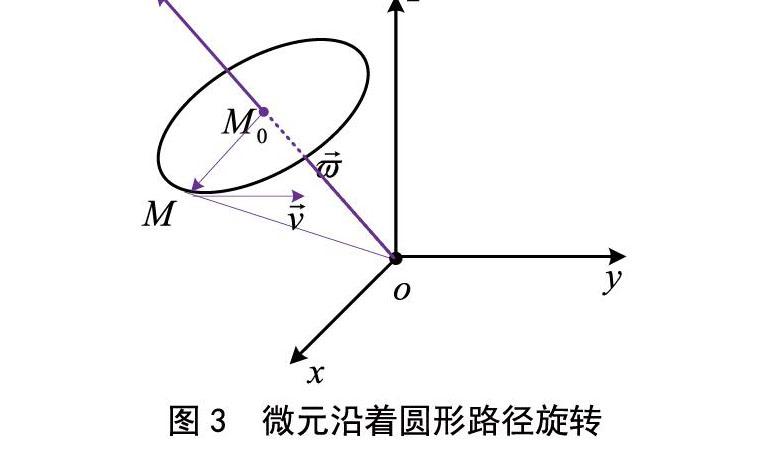
模型建立 ?以水漩渦為例，對漩渦中某一微元旋轉強度建立數學模型。度量水漩渦強度首先考慮微元旋轉一周的環流量。假設微元在水漩渦中隨著漩渦在做旋轉運動，微元旋轉運動假設為圓周運動（注：為了環流量的計算簡單，將數學模型簡單化）。微元循著圓形路徑轉動的角速度的坐標設為。圓形路徑中心點位置M0坐標設為（x0，y0，z0），微元某一時刻在圓形路徑中的位置M的坐標設為M（x，y，z），具體位置如圖3所示。

則微元在A（x，y，z）點的線速度為：

其中。

水漩渦中的微元沿著圓形路徑旋轉一周的環流量為：

通過公式（4）得出在單位時間內沿著空間曲線Γ的指定方向流過封閉曲線的流量，它的大小體現了空間曲線Γ所圍成的曲面Σ上的整體漩渦強度。如果微元運動到漩渦中心，要度量水漩渦中心位置處的微元旋轉強度，顯然環流量不夠充分。

漩渦中心位置處的漩渦旋轉強度可以借助圓形路徑Γ張成的曲面Σ面積（?Σ=Γ）趨近于零的極限來描述該點處的微元在水漩渦中心處的旋轉強度：

模型求解 ?公式（4）中微元繞圓形路徑環繞一周的環流量可以通過斯托克斯公式化簡為[2，10]：

其中

利用對面積的曲面積分中值定理可知，至少存在一點（ξ，η，ζ）∈Σ，有：

根據公式（8）和（14），可以得到漩渦中某微元在M（x，y，z）點處旋轉強度Φ的計算公式為：

旋度定義產生分析 ?公式（14）漩渦中某微元在M（x，y，z）點處旋轉強度Φ還可以用向量內積表示為：

通過公式可以進一步發現漩渦中某微元在M（x，y，z）點處旋轉強度Φ可以理解成新向量在法向量上的投影。綜上，微元在某處的旋轉程度可以用這個新向量來描述，故該新向量命名與旋轉有關，將其命名為旋度。

抽象的旋度定義：由于這個新向量產生是從水漩渦建模分析開始，結論與角速度有關聯，因此命名時考慮到渦旋強度的形象表達，還要注意與角速度有區別。微元在某處的旋轉程度用這個新向量來描述比較恰當，故該將其命名為旋度。拋開物理背景，給出旋度的具體定義。

旋度定義[5，10]：設向量場，其中P（x，y，z），Q（x，y，z），R（x，y，z）具有一階連續偏導數，點M（x，y，z）為場內一點，為向量在點M（x，y，z）處的旋度，記作。

思考（1）：旋度是度量微元在某點處的旋轉強度，角速度不能度量微元的旋轉強度。

本文建立的數學模型可以用角速度和徑向量的叉積表示線速度，因此，新向量，是角速度的二倍。如果是非速度場產生的某點處的渦旋強度，就沒有角速度倍數關系，甚至這個新向量與角速度沒有直接聯系。因此，微元在某處的旋轉強度用這個新向量表達更合適。

即使是線速度場，仍然不能用角速度度量微元在某處的旋轉程度。如以水流速度是否使得水中微元旋轉為例進行分析。設水流的速度場為，任意一點處的水流速度方向沒有改變，但是隨著水流的位置不同，速度的變化與位置的橫坐標有關。若將木制圓盤置于流水中，撞擊木制圓盤的流速不全部相同。由于沖擊木制圓盤的速度不同，木制圓盤邊緣處產生一個凈扭力，因此，木制圓盤發生轉動。如圖4所示，水流使得木制圓盤旋轉起來。

如果要度量水流中某一點處的旋轉程度，可以發現這個旋轉程度與角速度沒有聯系，而與水流速場產生的旋度場有關。在水流在每一點處均會有旋度，

此時的旋度分量與水流在該點處的位置有關，與角速度無關。

思考（2）：相關教材[2]將公式（5）稱為向量場在點M（x，y，z）沿法向量的環流量密度。通過公式推導，最后由公式（14）可以發現，公式（5）結果不能保證該值非負。本文將公式（5）描述成該點處的微元在漩渦中心處的旋轉強度是合理的。

3 結語

本文以物理現象水漩渦為例，對漩渦旋轉強度展開討論，教學設計中引入數學建模分析方法給出旋度概念。本文的研究結果表明，旋度用來測量微元在某一點處的旋轉強度，旋度場的產生與其相對應的向量場有關。

參考文獻

[1]劉志軍，劉鳳霞，等.渦旋波流場的渦量測試與計算及特征參數的影響[J].應用力學學報，2007，24（1）：6-10，169.

[2]朱士信，唐爍.高等數學（下）[M].北京：高等教育出版社，2015.

[3]任京男.關于場論中旋度的兩個重要問題[J].上海海運學院學報，1993，2（2）：58-63.

[4]黃輝，張小青.“電磁場”課程的散度和旋度研究型教學例析[J].電氣電子教學學報，2011，33（3）：99-102.

[5]斯徹.散度、旋度、梯度釋義[M].北京：機械工業出版社，2015.

[6]杜曉燕，張秀鋼，陸杰青.關于散度和旋度教學的幾點思考[J].電氣電子教學學報，2016，38（5）：81-83.

[7]黃國良，王瑞平，舒秦.矢量場散度和旋度的物理意義[J].西安礦業學院學報，1993，24（1）：71-77.

[8]李黎，張曉梅.旋度的一個物理解釋[J].中州大學學報，1995，12（2）：70-71.

[9]徐亮，蘭進，王明森，等.旋度對旋轉沖擊射流傳熱特性的影響[J].吉林大學學報：工學版，2018，48（5）：1483-1491.

[10]同濟大學數學系.高等數學（下）[M].北京：高等教育出版社，2007.

[11]孫遜，孫麟德.自由水渦內旋度檢測的數學方法探討[J].數學的實踐與認識，2015，45（1）：127-131.

[12]楊時中.講授梯度與旋度概念的體會[J].西安工業大學學報，1983（1）：85-93.