應用正交試驗分析電示功圖影響因子顯著性

，，， ，

(1.中聯煤層氣有限責任公司 晉城分公司，山西 晉城 048000；2.中國石油大學 機電工程學院，山東 青島 266580)

示功圖是煤層氣井生產管理與評價的重要參數，示功圖的準確獲取是分析井下工況的必要條件。通過電參數獲取示功圖，對排采系統工作參數影響因子進行分析，可以滿足煤層氣排采數據的不停產標定的要求，實現排采數據的實時、長期、連續監測。

影響電示功圖的因素眾多，例如系統轉動慣量、系統效率、電機特性等。由電參數反演計算示功圖過程中，難以定量測試和表征上述因素，并且各個變量的影響程度都為未知，故需對示功圖測試精度影響因子進行分析，而基于電示功圖的特征值數值模擬是一種行之有效的方法[1-5]。

本文從抽水機實際模型出發，建立電參數與載荷間的輸入輸出系統模型，提出一種基于優化算法，利用電參數間接獲得示功圖的方法。分析得出系統參數對測量精度影響的顯著性因子，利用正交分析法判斷各個影響因素對電示功圖特征值影響的大小順序，及各個影響因素與特征值的相互關系。實現參數的自修正和調整，提高測試的精度，為實現排采設備運行參數連續、可靠測試打下理論基礎，并通過現場測試進行驗證。

1 電示功圖求解

1.1 理論建模分析

為了求解抽水機的實際運動規律，建立抽水機的等效動力學模型。取曲柄為等效構件，如圖1所示。

圖1 抽水機系統等效構件

1) 運動微分方程建立。

根據系統動能定理，可得系統等效動力學方程為：

(1)

式中：Je為抽水機系統等效到曲柄軸處的等效轉動慣量，kg·m2；ω為等效構件曲柄角速度，rad/s；Me為抽水機系統等效到曲柄處的等效力矩，N·m；θ為等效構件曲柄轉角，rad。

2) 等效轉動慣量計算。

(2)

式中：J1為曲柄、減速箱和電動機等效到曲柄上的等效轉動慣量，kg·m2；J3為游梁系統繞游梁回轉中心的轉動慣量，kg·m2；ω3為游梁角速度，rad/s；ω1為曲柄角速度，rad/s。

3) 系統等效力矩計算。

為了計算等效力矩Me，需要計算抽水機系統的等效驅動力拒Md與等效阻力矩Mr。綜合帶入系統等效表達式中，可得系統等效力矩的表達式[6]：

(3)

式中：Me為等效力矩，N·m；i為電機到曲柄的傳動比；Md為電機驅動力矩，N·m；Mr1為曲柄系統阻力矩，N·m；Mr3為游梁系統阻力矩，N·m。

4) 等效動力學模型的求解。

由于Je和Me用解析式求解困難，用迭代法對方程進行求解[7]。將上式結合，用Δθ代替dθ，由此可解出ωi+1的表達式：

(4)

根據抽水機工況參數，給出等效構件曲柄的初值ω0，就可以求出曲柄任意時刻的角速度ωi。

1.2 Powell優化算法計算示功圖

電參數與載荷間具備輸入輸出關系，通過建立電參數與示功圖的目標函數，采用Powell算法反演計算懸點示功圖。Powell算法是一種局部多參數最優化計算，相對于全局優化算法有較快的收斂速度。在每一次迭代中，都要從初始點進行一維搜索，搜索方向是Powell算法中的另一個重要參數，用一個多方向集C表示。

Powell算法具體的優化過程分為若干次迭代，每次迭代都由N+1次一維搜索組成，其中N是搜索空間的維度。算法每次迭代過程的步驟是，從初始點開始，依次沿方向集的N個方向進行一維搜索，得到一個最優值及最優值對應的點。然后沿該點和初始點的連線的方向進行搜索，求得本次迭代的最佳值及其對應的點，然后把連線的方向替換為前N個方向效果不好的方向，形成新的方向集，進行下一次迭代[8]。

具體構造過程：

1) 將方向集Ci初始化：Ci=e(i=1,2,…,N，e為坐標軸的單位向量)。

2) 記錄初始點位置P0。

3) 從Pi出發，以此沿方向集的各個方向尋找該方向歸一化信息的極大值點，記該點為Pi+1，以該點為新的出發點，進行下一次迭代搜索。

4) 重復步驟3，直到新點和前一點之間的距離||Pi+1-Pi||<ε(ε為設定精度值)，該值為算法的解。

功率測試儀主要用來測量電機的功率值，可實現電參數連續、實時測量。實測電機輸入功率，讀取測試數據，取一完整周期功率數據，對測試數據進行平滑處理。通過動力學方程計算得到的曲柄真實角速度，根據曲柄一周的時間，得到曲柄角速度與時間的關系，進而將一個周期測試功率與時間的關系轉化為功率與角度的關系，便于與計算功率作對比。

根據建立的等效動力學模型，計算等效曲柄力矩M和曲柄真實角速度ω，則可得曲柄功率P。

P=Meωη

(5)

式中：η為系統總效率；P為計算曲柄功率，W。

建立測試功率與輸出功率誤差最小為目標函數。采用Powell優化算法，使目標函數最小，優化計算得到示功圖。

(6)

式中：F為目標函數，Pt為測試功率，W。

Powell算法是以共軛方向為基礎尋求最優解的算法[9]。給定初始載荷和誤差，采用Powell優化算法進行循環迭代計算，直至滿足計算誤差，計算得到示功圖。

1.3 算例分析

中聯某抽水機的型號為CYJ12-4.2-73HB，減速箱型號為JS-1000，電動機型號為Y280-S,沖程為4.2 m，沖次1.9 min-1，泵徑?56 mm，下泵深度為1 256 m。

測得煤層氣井驅動電機瞬時功率的條件下，運用等效動力學模型逆分析相關理論，編寫MATLAB程序，求解懸點載荷(示功圖)。編制Powell算法，以計算功率與實測功率誤差最小為目標函數，得到計算結果迭代過程如圖2～3所示。

圖2 懸點載荷迭代過程

圖3 誤差迭代過程

經過Powell優化計算得到懸點載荷，以此為基礎，通過抽水機系統動力學模型，計算曲柄真實角速度，由輸出轉矩得到曲柄瞬時功率，將計算功率與實測功率曲線進行直觀對比。得到計算結果曲線，如圖4所示。

圖4 示功圖對比

2 正交試驗分析

顯著性因素分析是在確定的目標函數影響因子范圍與特征值條件下，采用控制變量法，通過改變目標函數影響因子的數值，將正交分析法用于判別電示功圖影響因素的顯著性。設計正交矩陣，分析電示功圖影響因素的水平組合。用方差分析法對影響因子進行量化評價。本文對計算所得電示功圖影響因子設計正交試驗，進行顯著性分析。

另外，還應當投入專項資金，用來支持高校教育資源共享活動。在中觀層面上，地方政府要不斷加強對區域共享平臺的建設和完善，對有困難的高校采取一定的優惠政策，在經濟上提供支持。為使地方高校有更大的社會影響力，支持高校采用共享政策，積極引進教育資源。在宏觀層面上，國家和地方政府需要繼續加大對現有共享資源和平臺的投入力度，保證高等學校儀器設備和資源共享系統、中國高等教育文獻保障體系等正常且高效率地運行。同時，在網絡共享技術方面進行創新發展，為新的共享平臺的開發和建設加大投入。

2.1 影響因子的計算

系統效率的計算包括電機、皮帶和減速箱的效率。我國煤層氣井的抽水機采用同步永磁電動機，效率變化平穩，采用額定效率0.95。減速箱承受較大的轉矩和轉速，穩定效率為0.92。抽水機皮帶的正常工作效率有3種狀態[10]，如圖5。

圖5 皮帶效率的三個狀態

2.2 正交分析法

電示功圖影響因素顯著性分析，就是定量分析影響示功圖最大最小值、面積、斜率和各因素的相關性，即分析各個影響因素的變化對電示功圖的影響程度。本文采用正交分析法研究電示功圖最大最小值、面積、斜率對各個影響因素的敏感性，進而區分影響電示功圖的主要因素和次要因素。設計正交矩陣來分析電示功圖影響因素，用方差分析法對電示功圖影響因素的顯著性進行量化評價[11]。

正交分析法是一種統計方法，利用已有的正交表安排多因素實驗，再對結果進行統計分析的科學方法。利用正交分析法可以判斷各個影響因素對所考察指標影響的大小順序以及各個影響因素與考察指標的相互關系，采用方差分析法分析實驗結果，用各個影響因素的變差平方和與誤差平方和相比，作方差齊性檢驗，從而判斷實驗結果對各影響因素的敏感性[12]。

用正交表設計試驗計算方案，對試驗計算結果進行方差齊性檢驗，計算矯正數為

C=T2/n

(7)

試驗總偏差平方和為

SST=∑x2-C

(8)

試驗各影響因素偏差平方和及誤差平方和為

(9)

總偏差平方和自由度、單個影響因素偏差平方和自由度、誤差平方和自由度分別為

dfT=n-1

dfi=ki-1

(10)

方差齊性檢驗統計量Fj為[12]

Fi=(SSi/dfi)/(SSe/dfe)=(SSi/SSe)

(11)

式中：T為試驗指標之和，kN·m；n表示試驗數，無量綱；x為各試驗指標值，kN·m；SST為所有因素的偏差平方和總，(kN·m)2；SSe為誤差平方和，(kN·m)2；SSi為影響因素的偏差平方和，(kN·m)2；Ti為各因素同一水平試驗指標之和，kN·m；ki為各因素同一水平數，無量綱；dfT為總自由度，無量綱；dfi為各因素自由度，無量綱；dfe為誤差自由度，無量綱；Fi為構造的方差齊性檢驗統計量，無量綱。

2.3 正交試驗結果與分析

對上述得到的電示功圖進行影響因子顯著性分析。采用控制變量法，分別改變系統效率、電機特性和轉動慣量的值，計算得到不同影響因子的電示功圖對比曲線，如圖6～8所示。

圖6 不同效率狀態示功圖對比

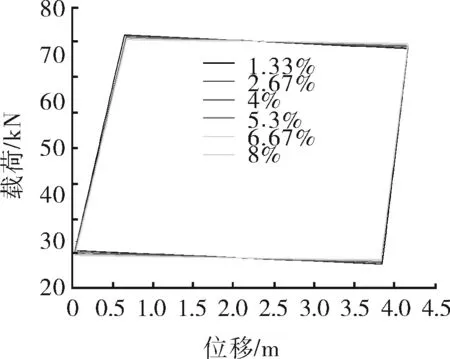
圖7 不同電機特性示功圖對比

圖8 不同轉動慣量示功圖對比

設置三水平三因素正交試驗，選取每組影響因子的3個典型數值進行顯著性分析，如表1所示。

表1 因素水平

根據正交分析法的設計原則，選取正交表為L9(33)正交試驗，為全面分析電示功圖對各個影響因素的敏感程度，設計9組計算、試驗，對電示功圖最大值、最小值、面積和斜率等特征值為計算結果進行方差齊性檢驗，如表2所示。

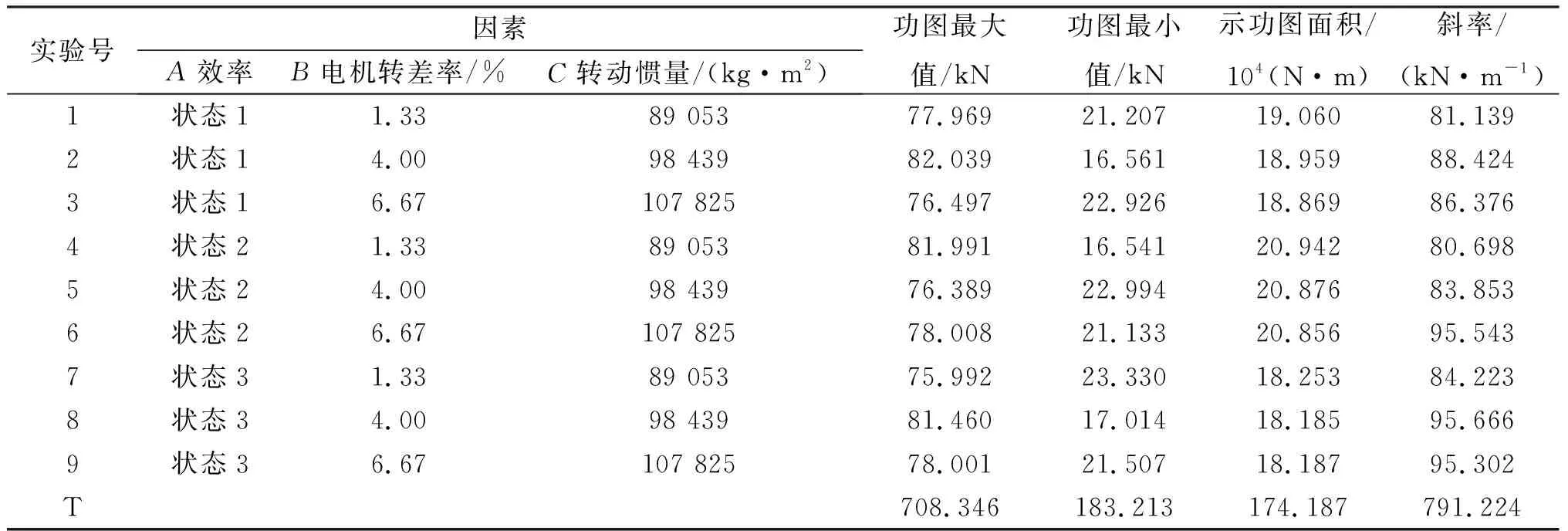
表2 實驗安排及計算結果

計算上述試驗的電示功圖如圖9所示。

對設計的正交試驗電示功圖最大值和最小值計算結果進行統計變量分析，如表3～4所示。其中，Ki表示正交試驗中任意列上水平號為i時所對應的試驗結果之和，ki表示Ki對應的平均值。

圖9 計算示功圖對比

表3 不同影響因子電示功圖最大值統計變量計算結果

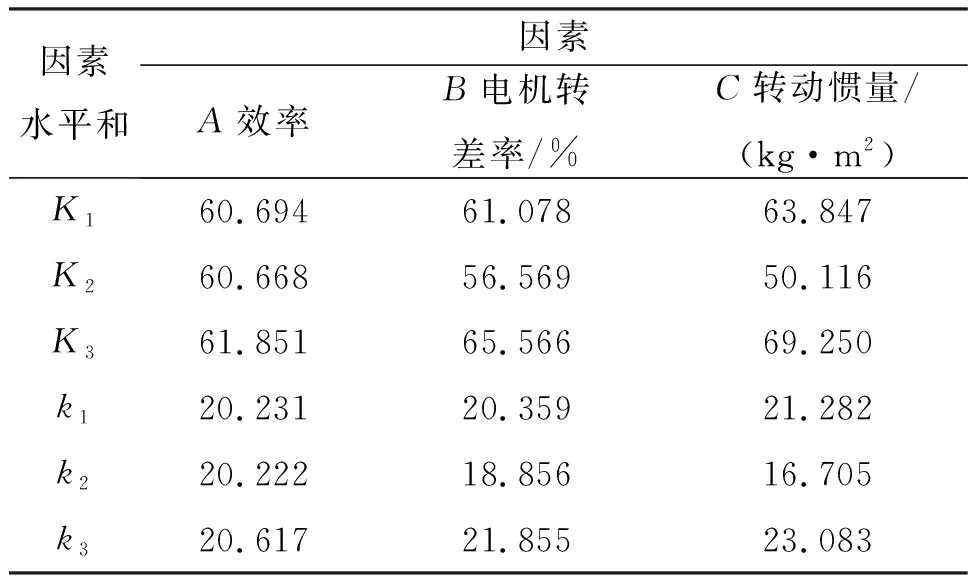
表4 不同影響因子電示功圖最小值統計變量計算結果

對設計的正交試驗進行方差分析，計算試驗電示功圖最大值和最小值總變異及誤差變異如表5～6所示。

表5 電示功圖最大值方差分析數據

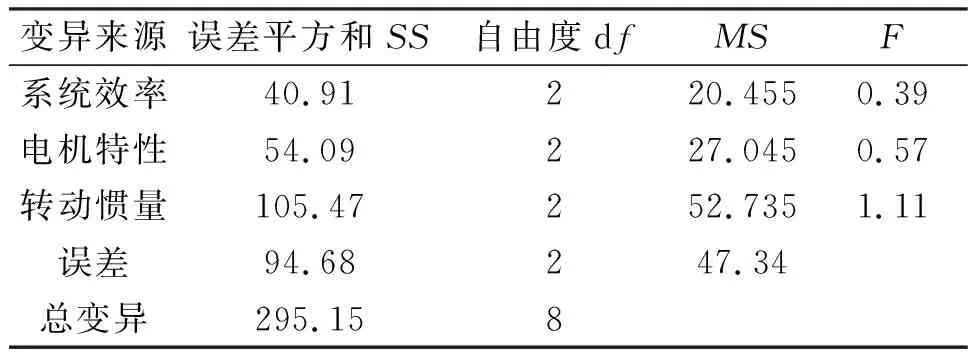
表6 電示功圖最小值方差分析數據

對設計的正交試驗電示功圖面積和斜率計算結果進行統計變量分析，如表7～8所示。

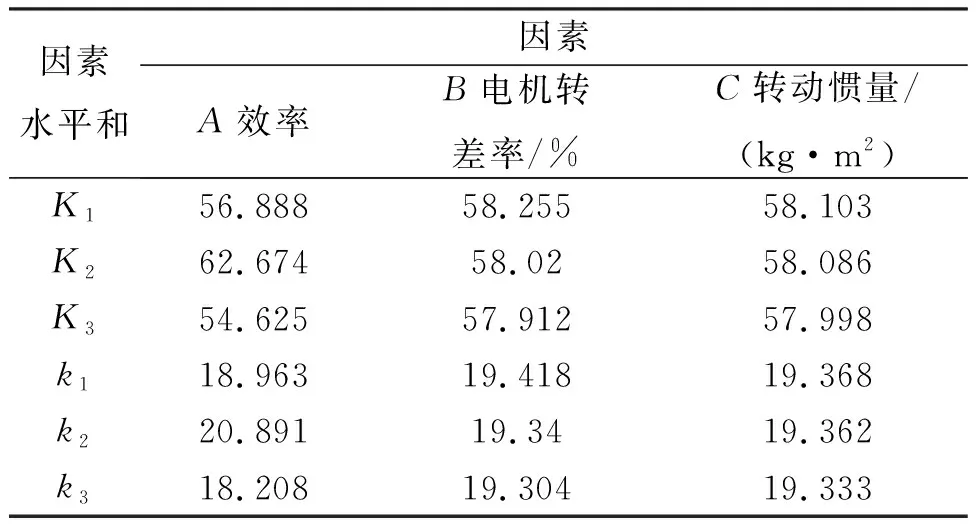
表7 不同影響因子電示功圖面積統計變量計算結果

表8 不同影響因子電示功圖斜率統計變量計算結果

對設計的正交試驗進行方差分析，計算電示功圖面積總變異及誤差變異，如表9所示。

表9 電示功圖面積方差分析表

對設計的正交試驗進行方差分析，計算電示功圖斜率總變異及誤差變異，如表10所示。

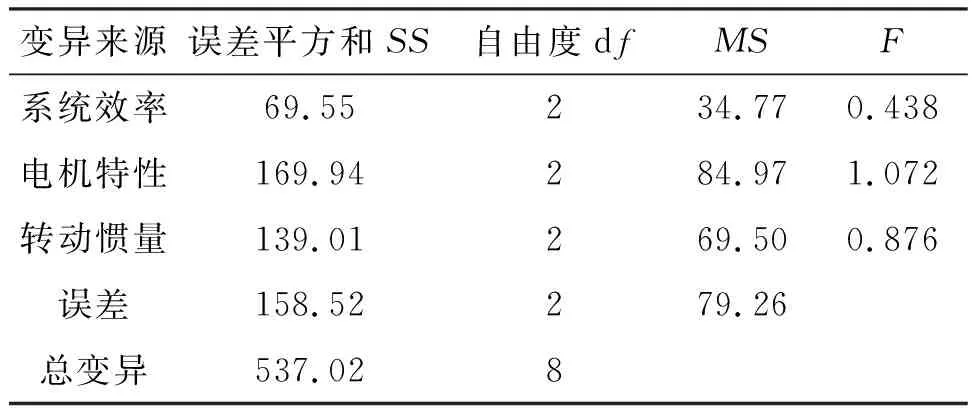
表10 電示功圖斜率方差分析數據

選取水平α為0.01，0.05，0.10，查方差齊性檢驗分布表可得：F0.99(4,4)=16，F0.95(4,4)=6.39，F0.90(4,4)=4.11，若Fi≥16.00，表示示功圖特征值對影響因素i高度敏感；若6.39≤Fi<16.00，表示示功圖特征值對影響因素i較敏感；若Fi<4.11，表示示功圖特征值對影響因素i不敏感。F檢驗結果表明，系統轉動慣量對電示功圖最大最小值影響最為顯著，系統效率對電示功圖面積影響最為顯著，電機特性對電示功圖的斜率影響最為顯著。

將不同電機特性與不同轉動慣量影響的特征值計算結果進行綜合，如圖10～11所示，根據計算結果可得示功圖斜率與轉差率關系式和最大值、最小值與轉動慣量關系式。

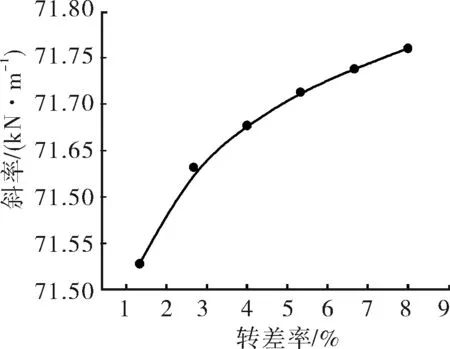
圖10 示功圖斜率與轉差率

圖11 示功圖最大、最小值與轉動慣量

斜率：k=0.127 8ln(100S)+71.498

(12)

(13)

3 結論

1) 為了分析影響煤層氣抽水機的電示功圖測試精度的因素顯著性，建立了抽水機的動力學模型，通過Powell算法得到最優示功圖。采用控制變量法改變目標函數影響因子數值，得到特征值變化。并結合正交分析法和方差齊性檢驗，確定特征值影響因子的顯著性。

2) 將正交分析法應用于電示功圖的各個影響因子的顯著性分析，能有效地區分影響電示功圖的主要因素和次要因素。各影響因素對電示功圖影響顯著性不同，影響電示功圖最大值和最小值由強到弱依次為：轉動慣量、電機特性、系統效率。影響電示功圖面積由強到弱依次為：系統效率、電機特性、轉動慣量。影響電示功圖斜率由強到弱依次為：電機特性、轉動慣量、系統效率。根據影響因子顯著程度，得到影響因子與電示功圖特征值的定量關系。

3) 通過建立系統參數對測量精度影響的顯著性因子，實現參數的自修正和調整，提高測試的精度，對實現煤層氣排采設備的自動化控制具有重要意義。