新興媒介環境下基于SIRS的應急物流信息傳播機理研究
(桂林理工大學 現代企業管理研究中心 廣西 桂林 541004)
一、理論回顧
關于社會關系網絡信息傳播機制,朱恒民,李青在新興媒介環境下以有向無標度網絡為載體提出輿情傳播SIRS模型。丁學君基于無標度網絡上SIR模型更加真實地描述社交網絡(SNS)中信息互動模式與輿情話題傳播過程與規律。鄭愛國在Centola提出的復雜傳染機制基礎上,從微觀層面對在線社會網絡信息的傳播問題進行了深入研究。
當前文獻關于應急物流信息研究主要是從信息平臺、信息系統、信息整合、系統內部信息傳遞等方面去研究,但是從疾病傳染視角去探討應急物流信息在廣泛社會范圍內傳播機制的研究很少。本文以加權無標度網絡為載體,運用SIRS模型更加明晰地刻畫新興媒介環境下應急物流信息廣泛傳播過程,揭示應急物流信息在社會關系中的傳播機理,推動應急物流大眾化。
二、基于加權無標度網絡SIRS的應急物流信息傳播
(一)信息傳播模型建立。基于上述定義構建加權無標度網絡中具有加權傳播率的SIRS模型的傳播力學方程如
其中:
(2)
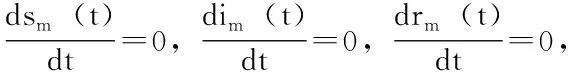
(3)
此時對于所有度為m的節點皆有im(∞)=0,這表明信息傳播過程結束時,不存在感染節點I,說明信息不曾在網絡中發生順利地傳播。要使信息在網絡中順利發生傳播,必須滿足ρ(∞)>0。
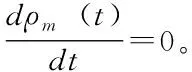
(6)
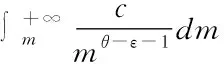
三、仿真分析
為了驗證和進一步具體闡述上述理論模型的有效性,通過仿真實驗模擬信息傳播過程,仿真過程中,設定網絡規模有限,且N=22000,網絡平均度為(m)=13。仿真條件下,網絡規模有限,所以這里mmin=7,mmax=19。考慮到新興媒介環境下社交網絡中信息傳播與感染性疾病傳播的不同情況,保持一定的信息治愈率ζ=3.8,和較高的免疫喪失率σ=0.899。
在這里首先假設加權無標度網絡中初始只有一個節點I0=1,分析模型處于穩態時受感染節點的比例i隨有效傳播率pc變化的變化情況。首先探討γ=1,ε<0時分別在五種不同取值情況下穩態感染節點的密度i隨傳播率p的變化情況,結果如圖1所示:
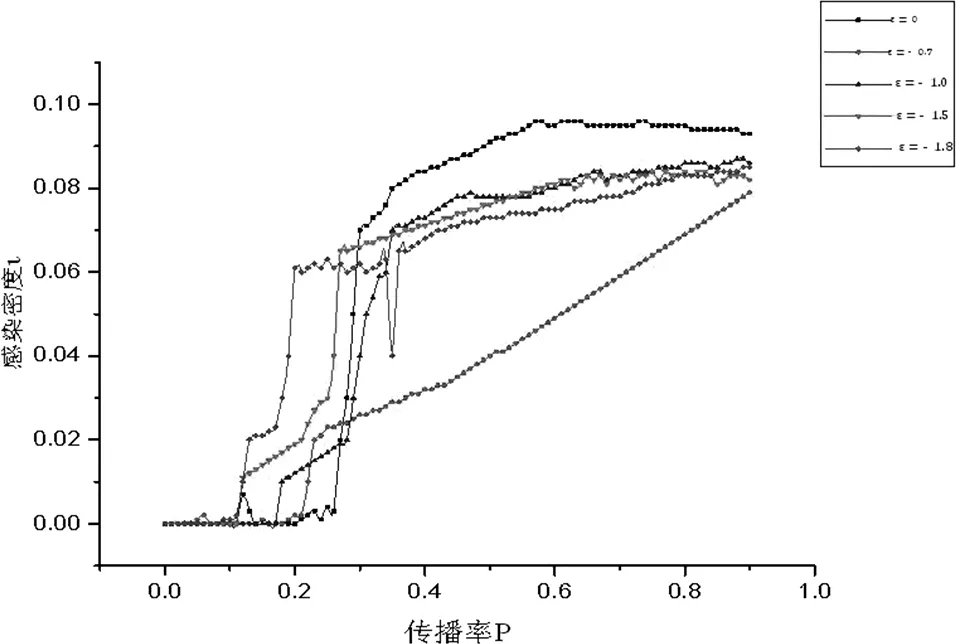
圖1SIRS模型穩態狀態下節點感染密度i與傳播率之間的關系(γ=1.0和ε=0,-0.7,-1,-1.5,-1.8)
由圖1仿真結果可知,當參數γ<0時,γ對節點感染密度i的增長速度有較大的影響,且參數γ的取值越小,穩態下節點感染密度i的增長速度就越快,傳播閾值也越大。此時有θ<ε+2+γ且θ→ε+2+γ,即θ的取值與ε+2+γ的取值無限接近。根據網絡規模有限情況下,傳播閾值的計算公式(22)可知此時有限傳播閾值較小。取α=1.01。
當ε=0時,
當ε=-0.7時,

