爆破荷載作用下淺埋高壓管道的應力變化規律
(1.中鐵港航-武漢科技大學爆破技術研究中心 湖北 武漢 430065;2.武漢科技大學 理學院 湖北 武漢 430065)
引言
地下管線系統是現代經濟建設與發展中不可缺少的一部分,隨著城市規模的日益擴張與經濟需求的快速增長,地下管網的作用愈加明顯,其安全運行得到了各部門的重視。隨著國家基礎設施建設規模的增長,原有地下管道附近進行爆破施工的情況時有發生,而爆破產生的沖擊波、地震波等有害因素就有可能危害到管道安全,因此,為確保施工過程中地下管網的安全,爆破振動下埋地管道的動力響應以及應力應變變化的規律研究成為爆破安全領域的熱點。近年來,國內外學者進行了相應的研究,取得了不少成果。張黎明[1]基于管道破壞的應變準則,利用相關的測試系統對工程爆破進行現場監測,建立了爆破振動質點峰值速度與管道破壞的對應關系。張紫劍等[2]利用相關測試儀對現場埋地管道的爆破振動和管道應變進行監控,得出不同頻率段的相關參數和薩氏公式有所不同,指出在實際施工過程中應結合具體情況確定爆破方案。房沖[3]等利用ANSYS/LS-DYNA對內空和充水管道在空爆下的管道動力響應情況進行了模擬對比,發現在等量炸藥下充水管道的形變量、單元位移和單元壓強峰值都低于內空管道。有許多學者[4-6]運用LSDYNA3D方法對下穿隧道掘進爆破時埋地管道響應規律進行模擬,發現管道壁厚減小或管道直徑增加會引起管道動應力增大,管道動力響應隨埋深增大顯著降低。馬東方[7]等人從動態、靜態兩個角度考慮,在爆破壓力下以及地震波的作用下,討論埋地管道的響應,在地下管道中,相對于環向位移,其徑向的位移響應要大的多,管道的在沿著徑向的位移的幅值較大,而環向的則較小。劉學通[8]等人對爆破振動下埋地管道動力響應研究進展進行了歸納和總結,并提出了今后對管道動力響應研究的主要方向和方法。劉建民[9]通過實驗對比分析了炸藥布置方式以及炸藥與管線相對位置對管線動力響應的影響。陳艷華等[10]結合液固耦合及天然地震荷載作用,探究了埋地管內不同運送液體密度及不同流量等因素對管道破壞的情況,得出油氣密度與管道破壞程度呈正比,油氣流速越快,破壞越嚴重。劉志偉[11]結合工程實際對施工時重型構件發生墜落對下方埋地高壓管道的動力響應情況進行了研究,提出了明確的管道保護措施。Abedi A S[12]等人將爆炸下管道模型簡化為兩端固定梁模型,建立四階非齊次偏微分方程,利用Fourier變換將時域問題變化為頻域問題解出偏微分方程,求得管道在爆炸波作用下的撓度。
但實際工程中,對于爆破振動對埋地內壓較高的高壓管道的影響研究還較少,由于高壓管道在爆破擾動下的受載情況更加復雜,現有的經典理論解決高壓埋地管道的爆破動力響應問題比較困難,而相關實驗研究消耗巨大且難以實施。LS-DYNA作為國際上廣泛運用的有限元分析軟件,兼具線性、非線性以及動力學、流固耦合計算功能,其解決實際工程問題的能力得到廣泛認可,基于此類有限元工具對高壓埋地管道的爆破動力響應問題進行數值模擬分析是較高效的手段。鑒于此,本文借助LS-DYNA,采用動力松弛法對管道內壓進行初始化,結合流固耦合算法模擬管道、土壤、罐內氣體以及炸藥之間的相互作用,研究淺爆破荷載作用下埋高壓管線的動力響應,分析管道的應力應變規律,以期為建立完善的管道近區爆破施工規范提供一定的參考依據。
一、理論分析
(一)管壁環向應力和徑向應力
高壓埋地管道可以近似看作受均布壓力作用的圓筒,如圖1所示,設圓筒內半徑為r,外半徑為R。在爆炸波傳來之前,管道內壓為q1,外部壓力(土壓力)為q2。
若在極坐標下系下的徑向坐標和周向坐標分別用ρ和θ表示,根據彈性力學基本原理,可以求得該問題的拉梅解答[13]如下:
(1)
由式(1)可知:當外壓為0,管道內壓單獨作用下的σρ總是壓應力,σθ總是拉應力;當內壓為0,外壓單獨作用下的σρ和σθ都是壓應力。可以推斷,由于內外壓對管壁的作用方向相反,二者疊加后會使管壁上σρ增大,而σθ減小。
土壤傳來的爆炸壓力q3作用在管壁外部,是外壓,如圖2,因爆炸應力波并非均勻作用在管道外壁,其對管道應力的影響比較復雜,可以用以下函數表示爆炸壓力作用下的管道應力:
(2)
將(1)、(2)疊加即為爆破荷載作用下高壓埋地管道管壁環向和徑向應力:
(3)
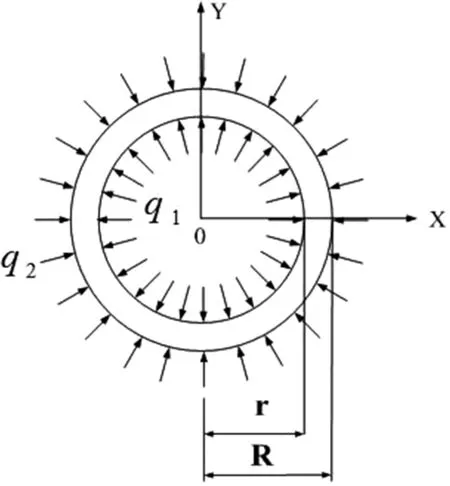
圖1 管壁受均布內外壓
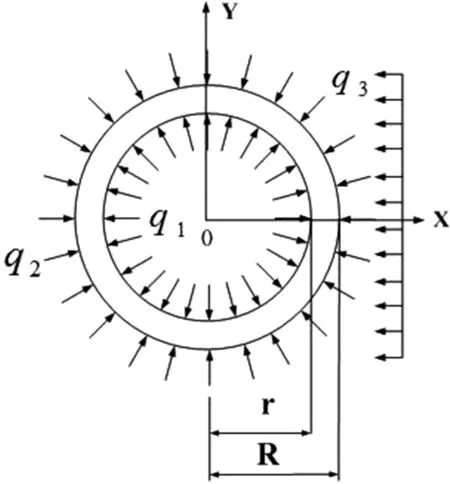
圖2 爆破荷載作用下的埋地高壓管道截面
(二)管壁軸向應力計算
假設管線水平方向分析模型如圖3所示,沿管線長度X方向的抗彎剛度為EI(z),單位長度的質量為m(z),作用在管上的橫向爆破荷載為q3(z,t)。
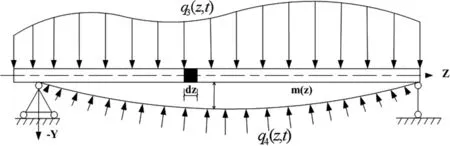
圖3 爆破荷載作用下高壓管道與土體作用
建立管道的彎曲積分方程為:
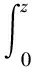
(4)
梁彎曲的最大彎曲正應力計算公式為:
(5)
式中W為管道抗彎截面系數,空心圓柱結構的抗彎截面系數為:
(6)
鋼管在工程中主要表現為塑性屈服,常采用Mises屈服準則[14]。一般在不受扭矩情況下,鋼制管壁上的主應力即為σρ、σθ、σz,則Mises等效應力為:
(7)
二、數值模擬
(一)模型建立
為了探究淺埋高壓管道在不同爆破位置爆炸對管道的影響,按照圖4所示的管線區域橫截面建立簡化模型。計算中涉及到炸藥、土壤、管道和空氣四者之間的相互作用,管道埋深為2m。管道尺寸[15]:外徑0.3m,內徑0.28m。根據文獻[9]和文獻[16]的研究內容,設計1#~6#六種炸藥布置工況,裝藥量均為1000g,其中1#~3#炸藥與管線中心水平距離分別為5m、3m、1m,4#~6#炸藥與管線中心垂直距離分別是1m、1.5m、2m,并且6#炸藥放置在地面。數值模擬中,取5m長管段建立三維模型,土體域為6m×5m×3m,空氣域在土體上方,高度0.5m。土體、空氣和炸藥采用ALE算法,用SOLID164單元劃分成六面體網格,管道采用LAGRANGE算法,用SHELL163單元劃分成四邊形網格。兼顧模擬精度和計算效率,通過試算確定網格尺寸控制在0.05m。最終建立的有限元模型如圖5所示,一共劃分了747100個單元。

圖4 埋地管線區域示意圖
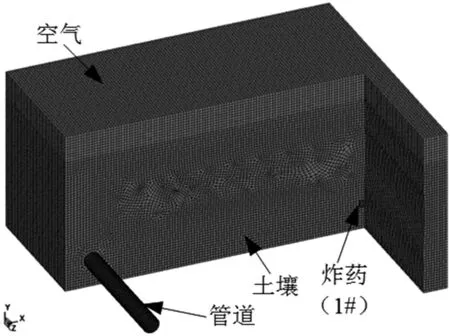
圖5 有限元模型
1.邊界條件
實際工程中,管線一般較長,并且爆炸應力波及地震波在泥土中的傳播距離也較大,為了更接近工程實際,將模型邊界均設置為無反射邊界條件。管道壁、管道內氣體以及炸藥之間的相互關系通過流固耦合關鍵字定義,采用罰函數的方式耦合各物質之間的物理量。管道和泥土的相互作用也采用多物質耦合算法實現。
2.材料模型及參數
(1)管道材料本構模型
管道材料為高強度鋼材,采用雙線性隨動硬化彈塑性本構模型模擬,密度為7850 kg/m3,泊松比為0.3,初始彈性模量為2.1×1011Pa,屈服應力為400 MPa,切線模量為5.0×108Pa。
(2)土壤材料模型及參數
土壤采用泡沫材料模型模擬,其基本物理參數如下:密度為1800kg/m3,剪切模量為1.601×107Pa泊松比為0.48,體積壓縮模量為1.328×1012Pa。
(3)炸藥模型及狀態方程
炸藥采用LS-DYNA自帶的高能炸藥模型模擬,采用JWL狀態方程進行爆轟壓力計算:
(8)
式中:P為爆轟壓力;E為炸藥爆轟產物的內能;V為爆轟產物的相對體積;A,B,R1,R2,ω—所選炸藥的性質常數。選取的炸藥材料及狀態方程參數如下表所示。

表1 炸藥材料及狀態方程參數
(4)空氣材料模型及狀態方程
空氣采用LS-DYNA中的NULL流體材料模型。空氣單元壓力采用線性多項式狀態方程模擬:
P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E
(9)
空氣狀態方程種各系數取值如下:C0=-1×105,C1=C2=C3=C6==0,C4=C5=0.4,E0= 3×105,V0=1.0。
(二)管道內壓初始化
高壓埋地管道的內壓是進行管道安全性設計不可忽略的因素。在進行淺埋高壓管道爆破動力響應的數值模擬時,應充分考慮管道在內壓作用下的初始應力靜平衡狀態。LS-DYNA的顯式求解能力處理爆炸與沖擊、結構碰撞、金屬加工成型等高度非線性的瞬態動力學問題是非常有效,但是在處理靜力學問題時,由于顯式求解器的特點,無法得到穩定的結果,而需要運用動力松弛的方式對靜態或者準靜態問題進行近似求解。動力松弛法是從空間和時間兩方面將結構體系離散化。空間上的離散化是將結構體系離散為單元和結點,并假定其質量集中于結點上。如果在結點上施加激振力,結點將產生振動,由于阻尼的存在,振動將逐步減弱,最終達到靜力平衡。計算中程序通過增加阻尼使結構動能逐步降低,求解器每隔一定的循環次數檢查動能狀態直到為0。本文采用這種方法對管道在內壓作用下的應力狀態進行初始化。根據規范[15]設計管道在內壓為10MPa的情況下,管壁第一主應力的初始化結果為146MPa,理論結果為140MPa,誤差不超過0.05。
(三)計算結果分析
1.管道的應力變化規律
為了探究爆破荷載作用下管道壁的Mises應力變化情況,如圖6所示,在管道模型上正對爆心截面選取四個單元考察應力沿管壁環向分布,并且在迎爆面沿軸向選取四個單元考察應力沿管壁軸向分布。輸出各工況下管壁不同位置的應力曲線如圖7和圖8。

圖6 考察單元位置
(1)應力沿管壁環向分布
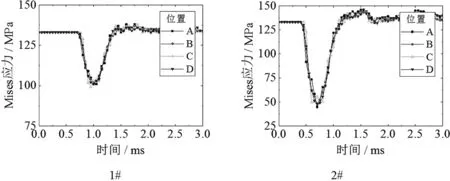

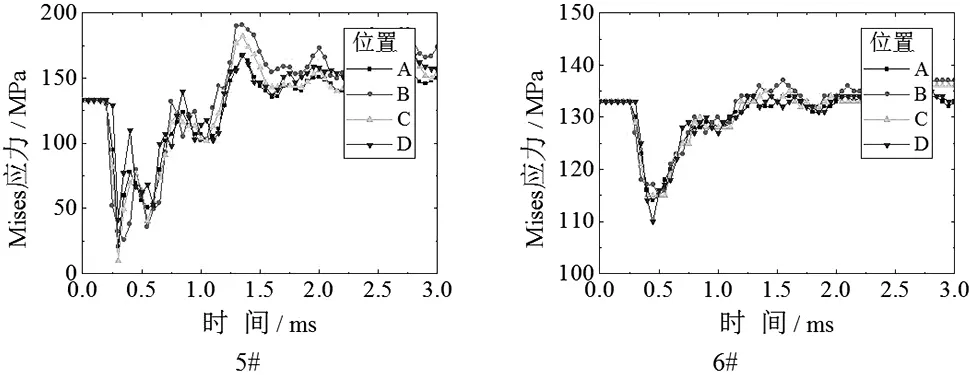
圖7 各工況下管壁環向不同位置的應力曲線
(2)應力沿管壁軸向分布
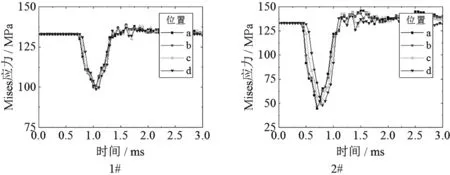
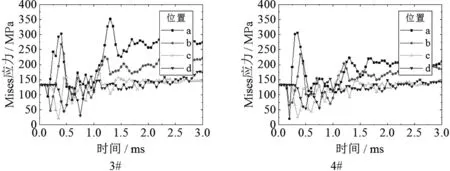
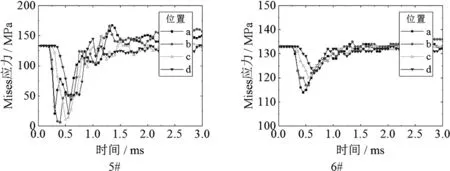
圖8 各工況下管壁軸向不同位置的應力曲線
由以上應力曲線可以看出,1#、2#、5#、6#四種工況在爆炸荷載作用下,管壁Mises應力較初始應力均有所減小。由前面的理論分析可知,這幾種工況下爆源距離管道較遠,管道撓度較小,管壁產生的軸向應力也很小,而爆炸荷載與管道內壓對管壁的作用方向相反,使管壁環向應力減小,所以最終Mises應力減小。而3#、4#工況爆源距離管壁較近,作用在管壁上的爆炸荷載較大,管道撓度較大從而使管壁產生很大的軸向應力,最終Mises應力增大。并且爆源距離較遠時,爆炸荷載對管道的作用較為均勻,管壁各處Mises應力曲線基本一致。
分析圖6中3#和4#工況下的應變曲線可以發現:3#工況下應變曲線出現的的第一個峰值最大位置是C點,第二個峰值最大位置是A點;4#工況下應變曲線出現的的第一個峰值最大位置是D點,第二個峰值最大位置是B點。其中A點和C點分別是工況3#和4#下正對爆源的位置,B點和D點分別是工況3#和4#下背對爆源的位置,當爆炸波傳來時,管道向爆炸波傳播方向彎曲,此時背對爆源的位置首先受拉,軸向拉應力急劇增大,所以第一個最大峰值出現在背對爆源位置;隨著爆炸波離去,管道在自身彈性力作用下恢復并在慣性作用下向正對爆源方向彎曲,此時正對爆源位置受拉,軸向應力急劇增大,所以第二個最大峰值出現在正對爆源位置。
2.管道的破壞形態
在裝藥量為1000g的情況下,1#~6#炸藥布置方式均未使管道發生破壞,說明這些工況下管道是安全的。但是,當藥量增大或者炸藥距離減小時,管道仍有可能因應力超過強度極限而發生塑性屈服。將3#工況藥量增十倍,管道的破壞過程如圖9所示。爆炸波傳到管道處時,管道正對爆源的位置首先發生屈服,隨后向后及兩端擴展,越靠近爆源的位置局部破壞越嚴重。
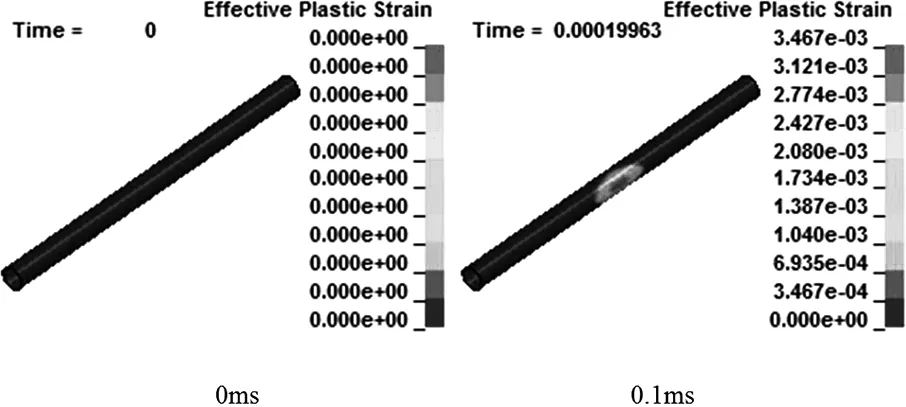
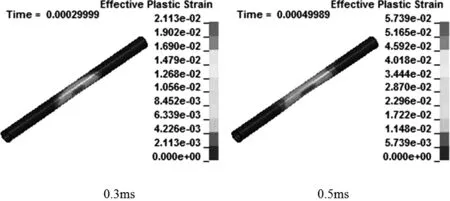

圖9 管道破壞過程
三、結論
根據彈性力學基本原理將埋地管道簡化成圓筒受壓力模型和彈簡支梁模型,建立了爆破荷載作用下淺埋高壓管道管壁環向應力、徑向應力和軸向應力的理論表達式。并運用LS-DYNA計算了不同工況爆炸荷載作用下管壁應力變化規律,可以初步得到以下結論:
(1)LS-DYNA的動力松弛法能有效對淺埋高壓管道進行應力初始化,內壓10MPa情況下的初始化結果與理論結果之間誤差不超過0.05。并且流固耦合算法能有效模擬爆炸荷載對管道的影響。
(2)在小藥量、遠距離爆炸荷載作用下,管道所產生的撓度比較小,軸向彎曲正應力很小,此時管壁主要是環向應力,而爆炸荷載和管道內壓的作用方向相反,對管壁環向應力的影響相反,因此,爆炸荷載作用下管壁Mises應力會略有減小。當距離減小或者藥量增大時,管道撓度增大,軸向彎曲正應力較大,此時管壁軸向應力占主導地位,雖然爆炸荷載作用下環向應力有所減小,但是Mises應力仍會增大。
(3)爆炸荷載對管道迎爆側正對爆源的位置影響最為顯著,總體呈現出從正面到背面逐漸減小、從正對爆源處到遠離爆源處逐漸減小的趨勢。
(4)爆炸荷載作用下淺埋高壓管道的破壞原因是管道撓度過大,管壁軸向應力增大,導致管道正對爆源位置應力超過強度極限而發生塑性屈服。算例中管道中部破壞情況最為嚴重。

