基于自適應螢火蟲算法的BP神經網絡股價預測

劉園園，賀興時

(西安工程大學 理學院，西安 710048)

0 引言

中國證券市場于20世紀末逐漸形成，經過20多年的發展，已成為國民經濟發展的重要組成部分。[1]隨著國民經濟的發展以及人們對投資理財的重視，股票投資受到越來越多的關注，因其收益比較高，并且股票的投資門檻較低，對于投資者來說是一個不錯的投資渠道，故逐漸成為大多數人的投資理財方式之一。然而國內股市發展時間較短，各類規章制度尚不夠完善。加之股市是一個極其復雜的非線性時變動態系統，股票價格受各種宏觀、微觀因素以及突發事件的影響[2]，股價的走勢往往呈現出較強的非線性特征。為了降低投資風險，保證穩定的投資收益，人們迫切需要一種合理的、有效的方法來掌握股價的變化規律，并預測其走勢[3]，因此研究股票市場，構建一種高效的股價預測模型，具有十分重要的現實意義。

股票預測即以股市信息及統計資料為依據，運用數學方法預測未來的股票價格。雖然學術界提出了多種方法來預測股價，如多元回歸、時間序列法、混沌理論、證券投資分析法等[4-7]，但由于諸多內部、外部因素的影響，致使股票預測時存在很多難點[8]，如存在高噪聲數據、股價波動呈非線性特點及投資者意向的不確定性，因此傳統的線性分析方法在解決此類非線性問題時有一定的局限性，預測結果難以令人滿意。人工神經網絡的非線性關系映射能力極強[9-10]，不需要構建非線性系統的數學模型或顯示數學解析式，便能夠實現任意維數向量之間的映射關系，非常適用于對股市等非線性系統的預測，其中BP(Back Propagation)神經網絡在此方面表現出了極其強大的能力。它不僅能夠將有關經濟活動類的知識從歷史數據中自動提取出來，還能夠克服傳統的定量預測方法中存在的諸多局限及困難，同時也能夠避免人為因素的影響。BP神經網絡的優勢雖然明顯，但也存在著諸多不足，如BP調整其權、閾值采用的是梯度下降法，這樣會導致網絡收斂速度慢且易陷入局部極小值點。因此，學者為了彌補算法自身的缺陷，將兩種以上的算法結合到一起，規避算法缺陷，凸顯算法優勢。目前主要研究成果有以下幾個方面：許曉兵等人[11]提出將小波變換和BP神經網絡結合的股價預測算法，對股票價格先去干擾再預測，能夠提高預測精度，但去干擾的參數選擇對于股價的預測影響較大。尹璐[12]提出了一種利用遺傳算法優化BP網絡初始權值和閾值，從而實現股價預測和發掘。但大量實驗表明，隨著時間的推移，該算法模型易使算法的絕對誤差呈上升趨勢變化。劉媛媛等人[13]提出了一種將遺傳算法與BP網絡相結合的算法，能夠提高收斂速度、改善尋優精度，從而提高預測精度。Huang Fu-Yuan等人[14]提出了一種利用蜂群算法來優化模糊神經網絡的股價預測算法，該算法提高了BP神經網絡的預測性能。

智能算法近年來受到諸多學者的關注，如遺傳算法、蟻群算法、布谷鳥算法、螢火蟲算法等，其中螢火蟲算法(Firefly Algorithm,FA)[15]概念簡單，流程清晰，需要調整的參數較少，收斂速度較快，同時搜索精度較高，更加容易實現。本文在詳細研究了標準BP算法和標準FA算法原理的基礎上，針對FA算法存在的缺陷，通過將混沌優化方法應用到螢火蟲算法中，并對螢火蟲算法中的步長因子進行自適應調整，提出了一種自適應螢火蟲優化算法(SFA)；針對BP算法的不足，提出了利用自適應的螢火蟲算法優化BP神經網絡的方法，改善股票的預測精度、提高BP算法的收斂速度，據此對4種股票指數走勢進行預測。通過與傳統BP神經網絡、基于FA算法的BP網絡模型(FA-BP)對比，發現基于SFA算法的BP網絡模型(SFA-BP)明顯優于另外兩種模型，能有效預測股票價格。

1 FA-BP神經網絡

1.1 螢火蟲算法

螢火蟲算法(FA)的核心思想是通過亮度比較來調整位置、更新數據，即亮度大的螢火蟲吸引亮度小的螢火蟲向其移動，同時兩者均更新自身位置。故亮度、吸引度、位置更新公式為螢火蟲算法中的幾個要素。 當螢火蟲i的亮度大于螢火蟲j的亮度時，螢火蟲j向i移動。故有如下定義：

(1)螢火蟲i對j的相對亮度為：

(1)

其中：Ii為螢火蟲i的最大熒光亮度；γ為光強吸收系數，通常設為常數；rij為螢火蟲i到j的空間距離。

(2)螢火蟲i對j的吸引力為：

(2)

其中：β0為在光源(r=0)處的吸引力，是最大吸引力。

(3)螢火蟲j向i移動并進行位置更新，螢火蟲j的位置更新公式如下：

Xj(t+1)=Xj(t)+βij(Xi(t)-Xj(t))+α(rand-1/2)。

(3)

其中：t為迭代次數；Xi、Xj表示螢火蟲i與j的空間位置；步長因子α為[0，1]上的常數；rand是[0,1]上的隨機因子，且服從均勻分布。 由于其他螢火蟲無法吸引最亮的螢火蟲，故最亮的螢火蟲位置更新公式不能按式(3)執行。

下面給出最亮螢火蟲位置更新公式：

XB(t+1)=XB(t)+α(rand-1/2)。

(4)

基本螢火蟲算法步驟如下：

Step 1：設置相關參數，隨機初始化n個候選解作為螢火蟲的初始種群。

Step 2：計算適應度值，更新空間位置，重新計算各螢火蟲的亮度、吸引度，計算移動到的新位置。

Step 3：評估新解，更新螢火蟲熒光亮度，排列各螢火蟲，并且找出當前最優解。

Step 4：移動最亮螢火蟲。

Step 5：判斷是否滿足迭代結束條件：若滿足，轉至Step 6；若不滿足，轉至Step 2。

Step 6：輸出結果。

1.2 BP神經網絡

BP神經網絡作為目前應用最為廣泛的一項人工神經網絡[16-18]，是基于反向傳播的多層前饋式網絡，其特點是信號正向傳播、誤差反向傳播。BP網絡一般為三層結構的網絡，即輸入層、輸出層和隱含層，隱含層可為單層或多層。各層間的神經元僅和相鄰層神經元之間通過權值傳遞信息，同層神經元之間無連接。假設網絡的輸入層神經元個數、隱含層神經元個數、輸出層神經元個數分別為n、m、s，則BP神經網絡結構即為：n-m-s。

BP神經網絡算法步驟如下：

Step 1：初始化各層之間的連接權值、閾值，ωij為輸入層和隱含層間的連接權值，ωki為隱含層和輸出層間的連接權值，θi為隱含層閾值，αk為輸出層閾值，均取[0,1]區間內的隨機值。

Step 2：選擇一個樣本作為輸入樣本xj進行訓練，則隱含層第i個節點的輸入變量zi、輸出變量yi如下：

(5)

(6)

Step 3：通過確定隱含層輸出變量yi，則輸出層第k個節點處的輸入變量mk、輸出變量nk、輸出變量與實際輸出值Ok的均方差E如下：

(7)

nk=ψ(mk)，

(8)

(9)

Step 4：比較E的值與訓練目標誤差值的大小：若小于誤差值，則返回Step 2，選擇下一個樣本；反之進行誤差反向傳播，修正各層連接權值、閾值，直至滿足誤差要求。其中應用梯度下降法獲得權值的學習率η的修正公式如下：

(10)

其中：

(11)

(12)

則輸出層的權值修正公式如下：

Δωkj=-?(Ek-nk)ψ′(mk)yi。

(13)

同理，可得閾值的修正公式。隱含層的權值、閾值修正公式亦可得。

Step 5：選擇下一個樣本，返回Step 2繼續訓練，直至將所有樣本訓練完。

1.3 FA-BP神經網絡

傳統的BP神經網絡是基于梯度下降法獲得的權值和閾值，是隨機的，且收斂速度較慢，易陷入局部極小值點。而通過BP神經網絡和螢火蟲算法相結合的方法(FA-BP)可以在一定程度上改善BP算法的不足。其基本思想是：首先由輸入和輸出的參數將BP神經網絡的結構加以確定，這樣也就能夠將螢火蟲算法內每個螢火蟲個體的編碼長度加以確定。每個螢火蟲個體都包含了BP網絡的所有權值、閾值，且螢火蟲個體的維度與BP網絡中起作用的權值和閾值的總個數相對應。再根據適應度函數計算每個螢火蟲個體的適應度值，并且進行迭代，更新亮度、吸引度、位置等信息，找到最優個體，然后將得到的螢火蟲個體信息給BP網絡賦值，作為其初始權值和閾值，最后通過BP算法進行股價預測，從而得到精確度較高的預測結果。

但是，傳統的螢火蟲算法存在對初始解較為依賴、迭代后期收斂速度較慢、搜索精度不高等缺陷。為解決這些問題，提高算法的全局搜索效率，本文提出了一種利用自適應的螢火蟲算法來優化BP神經網絡的方法，并構建了模型(SFA-BP)，從而獲得最優的初始權值和閾值，提高預測精度。

2 自適應螢火蟲算法(SFA)

2.1 混沌映射

混沌是一種復雜的非線性系統動態行為，因其具有對初值敏感依賴性、遍歷性、隨機性等優點，近些年得到廣泛關注，還被廣大學者應用到啟發式算法中，將其與啟發式算法相結合，提高算法的尋優性能。基本思想是把優化變量空間通過混沌映射線性地映射到混沌變量中，再根據混沌變量的遍歷性、隨機性進行優化搜索，最后將得到的解線性地轉化到優化變量空間。

Tent映射混沌序列分布均勻，并且搜索效率較高，有更快的收斂速度，其數學表達式為：

(14)

該映射經貝努力移位變換后數學表達式為:

xn+1=(2xn)mod 1。

(15)

2.2 Tent混沌優化

利用混沌序列優化螢火蟲算法已經受到眾多學者的研究，本節利用Tent映射具有更好的遍歷均勻性及更快的搜索速度的特點，優化螢火蟲算法，其基本思想如下：

(1)利用Tent映射初始化種群。利用Tent映射隨機產生分布均勻的初始種群，這樣既能保證初始種群個體的隨機性，又能使種群多樣性得以提升，從而提高算法的收斂速度。

(2)自適應動態調整較優解混沌搜索。本文假設算法第i只螢火蟲在尋優時出現停滯。對當前進化第t代的所有螢火蟲按適應值從大到小排序，取前百分之p個個體n(其中p=5)，分別求出這n只螢火蟲第d維的最小值Xdmin和最大值Xdmax作為混沌搜索空間。并從這n只螢火蟲中隨機選擇1個螢火蟲位置XB作為基礎解，產生Tent混沌序列，進而用產生的混沌序列中的最優解更新螢火蟲位置，使算法跳出局部最優。

利用Tent映射對種群中較優解進行局部搜索的主要步驟如下：

Step 1：在螢火蟲種群Xi(i=1,2,…,n)中，從前百分之p個個體當中隨機選擇一個螢火蟲位置XB作為基礎解。

Step 2：利用式(16)將XB映射到(0,1)，其中i=1,2,…,n；d=1,2,…,D。

(16)

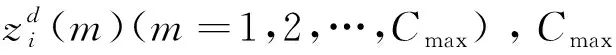
(17)

Step 5：計算XC的適應度值，并與XB的適應度值作比較，保留最好的解。

Step 6：如果達到最大混沌迭代次數，運行結束，否則轉至Step 3。

2.3 選擇策略

錦標賽選擇策略是一種基于局部競爭機制的方法，即從種群當中隨機選出q個個體進行比較，并且將適應度大的個體作為最優個體。本文中螢火蟲采用錦標賽選擇策略進行群體位置更新，并且取q=2，給適應度大的個體加1分，所有螢火蟲進行此過程，最終得分最高的螢火蟲個體其權重也最大。因為該選擇策略僅將適應度值的相對值當作選擇的標準，而對適應度值的正負不作要求，故能避免超級個體對螢火蟲算法的影響。適應度選擇概率為：

(18)

其中：ci為每個個體的得分。

2.4 自適應步長

基本FA算法中步長因子α為常數，采用的是[0,1]間的固定值，且在迭代過程中值不變。較大的α在進化初期有利于算法的全局搜索，但進化后期會降低搜索精度，容易出現震蕩現象，不易找到全局最優解；較小的α在進化后期有利于算法的局部搜索，搜索精度較高，但將導致算法收斂速度過慢等問題。本文采用隨著迭代次數而遞減的 α，從而使算法具有更快的搜索速度和搜索精度，α計算公式如下：

αt+1=αtδ，0.5<δ<1。

(19)

其中：δ為冷卻系數，通過式(19)迭代計算得到的α，每次會得到一個更小的值，從而能更好地平衡螢火蟲算法的全局搜索能力和局部開發能力。

2.5 SFA算法

SFA算法采用Tent混沌優化、錦標賽選擇策略和自適應步長參數優化方法，避免算法早熟收斂及陷入局部極值，具體算法流程如下：

Step 1：設置相關參數：螢火蟲種群規模n、最大迭代次數T抑或求解精度σ、步長因子α初始值、最大吸引度β0、光強吸收系數γ、位置維數D、混沌搜索最大迭代次數Cmax。

Step 2：設置迭代次數初始值t=0，在可行域中利用Tent映射初始化種群，隨機初始化n個D維候選解作為螢火蟲的初始種群Xi(i=1,2，…,n)。

(20)

Step 3：根據適應值函數f(Xi)計算各螢火蟲的亮度I(Xi)。初始標志向w(i)=0，記錄最亮螢火蟲為同一螢火蟲的次數。

Step 4：每只螢火蟲都會向著比自身亮的螢火蟲移動，更新螢火蟲之間距離，更新吸引度值，根據式(19)更新步長因子，根據式(3)或(4)進行位置更新，計算亮度。

Step 5：如果f(Xj)>f(Xi)，則Xi=Xj，w(i)=0；反之保持原解Xi不變，w(i)=w(i)+1。

Step 6：利用錦標賽選擇策略，通過式(18)計算選擇概率Pi(t)。

Step 7：螢火蟲根據概率Pi(t)選擇最亮螢火蟲，從而確定自身位置更新，計算適應度值，轉至Step 5。

Step 8：若w(i)>Limit，則第i只螢火蟲為停滯解，根據第2.2節的自適應混沌搜索產生一個新解替換停滯解。

Step 9：記錄當前所有螢火蟲自身的最優解，保存種群當前最優解。

Step 10：更新t=t+1，判斷是否達到求解精度σ要求或滿足最大迭代次數T。若滿足，則輸出當前最優解；反之返回Step 4。

3 SFA-BP神經網絡

3.1 個體編碼

本文采用實數編碼的形式，將BP神經網絡的連接權值和閾值表示為螢火蟲個體。該個體被映射為4部分，即輸入層到隱含層間的連接權值ωij、隱含層的閾值θi、隱含層到輸出層間的連接權值ωki、輸出層的閾值αk。由于輸入層節點個數為n、隱含層節點個數為m、輸出層節點個數為s，因此，螢火蟲個體的字符串長度為：L=n×m+m+m×s+s。

各連接層之間的權值和閾值表示如下：

(21)

θi=[θ1,θ2,…,θm]Τ，

(22)

(23)

αk=[α1,α2,…,αs]Τ。

(24)

則螢火蟲個體的編碼形式為：

X= [ω11,ω12,…,ω1m,ω21,ω22,…,ωnm,θ1,θ2,…,θm,

ω11,ω12,…,ω1s,ω21,ω22,…,ωms,α1,α2,…,αs]。

(25)

3.2 評價標準

本文將網絡的實際輸出值和真實值之間的均方誤差作為BP網絡的評價標準，因此在螢火蟲算法中可將適應度函數設置為：

(26)

其中：N為輸入的樣本總數，yi為預測的股票價格，xi為真實的股票價格。fitness的值越小，表示網絡的性能越好。

3.3 算法實現的基本步驟

根據傳統BP神經網絡的實現步驟及自適應螢火蟲算法的實現步驟，得到基于自適應螢火蟲算法優化的BP神經網絡(SFA-BP)的算法實現步驟如下：

Step 1：初始化參數：初始化SFA算法以及BP算法的參數，并設置最大迭代次數。

Step 2：編碼：采用實數編碼方法，依照式(25)將BP的權值和閾值統一編碼，并對應到螢火蟲個體中，使得每個螢火蟲個體代表一個BP網絡結構。

Step 3：根據2.5節自適應螢火蟲算法步驟，找出當前最優解。

Step 4：解碼：將螢火蟲個體解碼，得到相應BP網絡的權值和閾值。并以此作為BP的初始權、閾值，進而訓練BP神經網絡。

Step 5：判斷是否達到BP網絡停止條件：若滿足，得到最優的神經網絡結構;反之，繼續訓練。

4 仿真實驗與結果分析

4.1 FA與SFA性能對比分析

由上文可知，載有BP神經網絡初值信息的螢火蟲個體進行尋優，然后將輸出的最優值解碼為神經網絡的權值、閾值，因此FA-BP、SFA-BP算法性能的好壞在一定程度上依賴于FA、SFA算法的性能。為了評估FA、SFA算法的優化性能，本文選取4個標準測試函數來進行仿真實驗，這4個測試函數表達式、搜索區間和最優值如表1所示。

表 1 4個基準測試函數

這些測試函數均為國際通用的全局優化問題常用的測試函數，分別具有不同的特性，可用來充分考察算法的尋優能力。其中，Rosenbrock和Sphere是單峰函數，這些函數可以用來測試算法的尋優精度、收斂速度和執行效率；Rastrigin 和Ackley為多峰多極值函數，這些函數的特點是有許多局部極值，可以用來考察算法的全局尋優能力、跳出局部極值點和避免算法早熟收斂的能力。將標準FA算法和SFA算法進行對比實驗。所有實驗均在硬件環境為Intel Core I5-7200，CPU 2.70 GHz，內存4 GB；軟件環境為Windows 10操作系統的計算機上進行，所有算法在Matlab R2016a下進行仿真。

在實驗中，算法的相關參數設置為：螢火蟲種群個數為100個，最大迭代次數為2 000次，最大吸引度β0=1，步長因子初值α=0.05，光強吸收系數γ=1.0，函數維數設置為30。相比FA算法，SFA算法又引入了3個參數，參數值的設定分別為混沌搜索次數為30次、δ=0.97、Limit=100。為了避免算法偶然性帶來的誤差，每個測試函數分別獨立運行30次，并統計其結果。規定當求解精度達到10-20時假定結果為0，通過記錄FA算法和SFA算法在迭代后的平均值、最優值、最差值、平均運行時間等來評價各算法的優化性能，平均值、最優值、最差值反映的是解的質量，平均值反映的是算法所能達到的精度，平均運行時間反映的是算法的尋優速度。測試結果比較如表2所示。

由表2可知，SFA算法的尋優精度明顯優于FA算法，無論是對于單峰函數還是對于多峰函數，SFA算法的收斂速度均明顯優于FA算法。

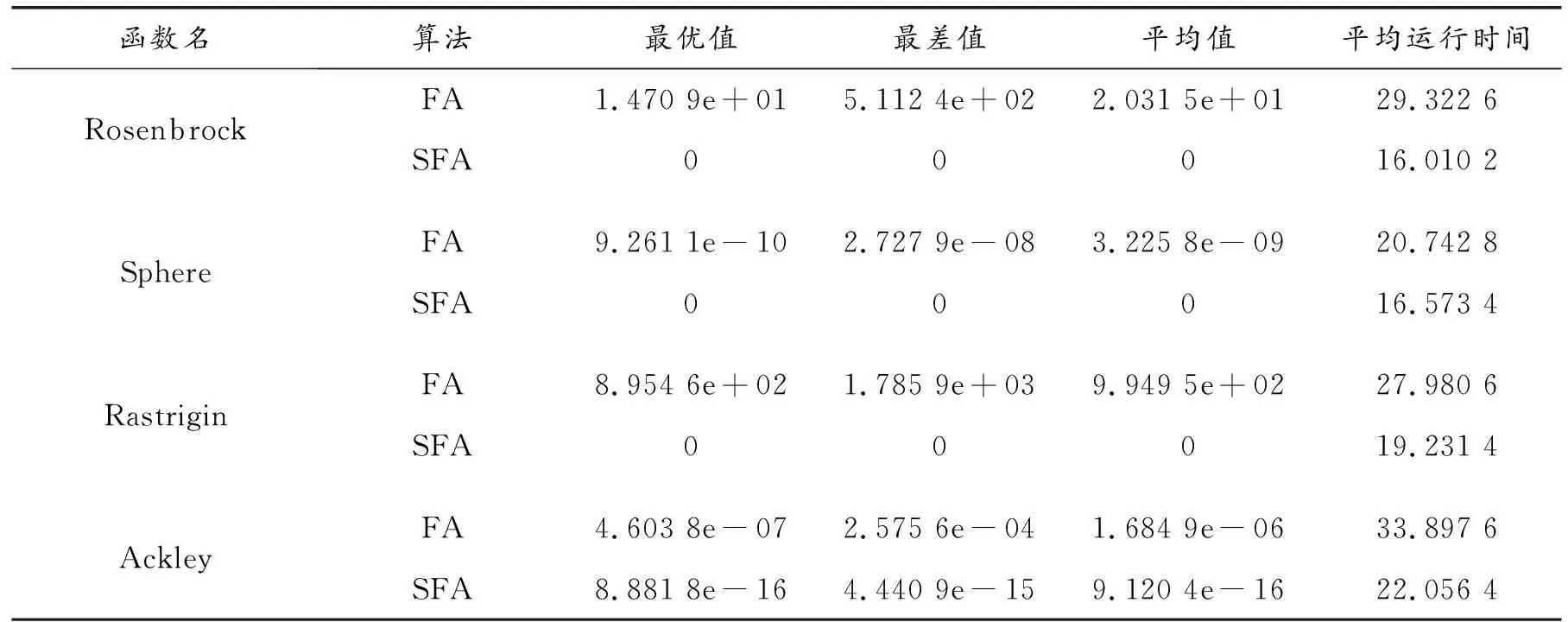
表2 FA算法和SFA算法測試結果比較

對于單峰函數Sphere,SFA算法在尋優精度、尋優率及收斂速度方面均明顯優于FA算法，能夠持續有效地搜索函數全局最小值。對于非凸病態單峰函數Rosenbrock而言，因其在取值范圍內走勢較平坦，可收斂至全局最優點的機會很少，但SFA算法依然表現出了強大的全局尋優能力；對于多峰函數Rastrigin和Ackley函數,SFA算法的求解精度及收斂速度均高于FA算法，主要由于SFA采用自適應Tent混沌搜索和自適應步長因子，不僅能動態調整混沌搜索空間，還能動態調整步長，因而既能保證種群多樣性、提高求解精度和收斂速度，也能使算法跳出局部最優。故初步推斷SFA-BP預測精度優于FA-BP。

4.2 樣本數據準備

BP網絡進行預測時，若樣本個數太少，會導致網絡的泛化能力較弱；反之，樣本個數太多，又會出現過擬合現象。因此，樣本個數的選取應當適中。本節選取了4種股票指數從2015年1月5日—11月12日的歷史收盤價數據，分別是中證1000指數、深證1000指數、上證商業指數及香港恒生指數。中證1000指數能夠整體反映滬深證券市場內小市值公司的綜合狀況，深證1000指數，旨在反映深圳證券市場內大中小市值企業的整體狀況。上證商業指數能總體反映多種行業的景氣情況及其股價的波動情況，香港恒生指數在反映香港整體股市價幅趨勢中是最具權威影響的股價指數。

4.3 網絡結構的設計

(1)網絡層數的確定。Cybenko等人[19]已經用理論證明，三層的BP網絡能夠以任何精度逼近任意非線性函數。因此本文選擇三層BP網絡進行研究，即只含一個隱含層的BP神經網絡。

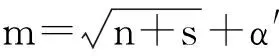
(3)其他參數的確定。利用隨機函數設置初始權值，通常為(-1,1)之間的隨機數，學習步長取0.2，期望誤差取0.000 1，螢火蟲種群個數取100個，最大迭代次數取2 000次,步長因子初值α=0.05,最大吸引度β0=1,光強吸收系數γ=1.0。相比FA算法，SFA算法又引入了3個參數，參數值的設定分別為混沌搜索次數為30次,δ=0.97，Limit=100。

4.4 預測結果及分析

本文通過已選取的股票數據，對BP網絡模型、FA-BP網絡模型和SFA-BP網絡模型進行股價預測精度的仿真對比分析。表3為3種算法對4種股票指數預測的平均誤差數據對比。

由表3的統計結果可以看出，對于4種股票指數數據而言，SFA-BP網絡模型的預測精度最高，明顯優于BP網絡模型及FA-BP網絡模型的預測精度，具有一定的實際應用價值。

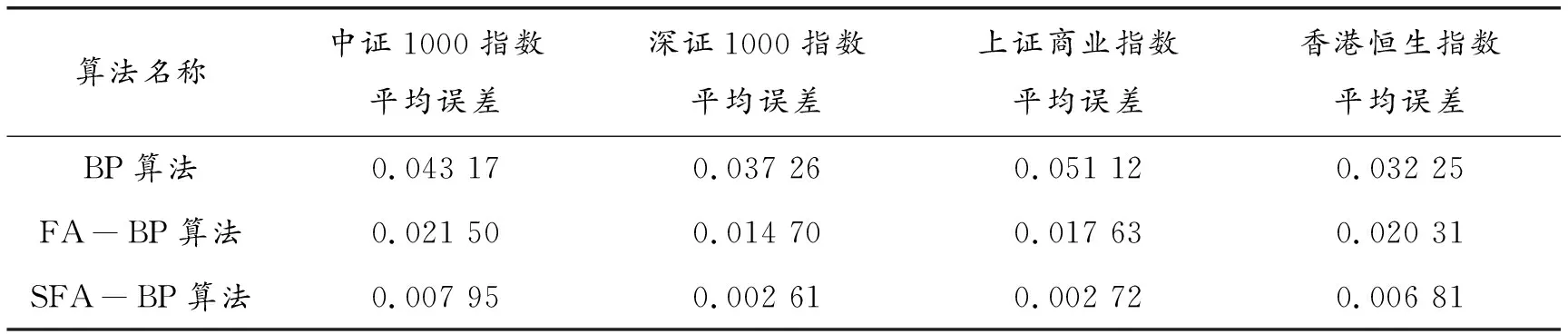
表3 BP算法、FA-BP算法和SFA-BP算法誤差對比

5 結語

為了克服傳統BP網絡收斂速度慢、容易陷入局部極值點等不足，提出了利用自適應的螢火蟲算法(SFA)來優化BP網絡的方法，構建了BP優化模型(SFA-BP)，并將其用于股價預測，構建了股票價格的預測系統模型，通過仿真實驗可以看出，該預測系統取得了較為理想的預測效果，在實際生活與工作中，具有一定的實用價值。但股票價格預測作為一個長期的工作，若能擴大其樣本規模，將開盤價數據、最高最低價數據、成交量數據等引入，將進一步提高預測精度，進行更為精確的預測，將有更好的應用前景。