“定積分存在的條件”問(wèn)題情境教學(xué)設(shè)計(jì)
——從Riemann函數(shù)看Riemann積分

（湖南城市學(xué)院理學(xué)院 湖南益陽(yáng) 413000）

一、內(nèi)容分析

定積分是理解《數(shù)學(xué)分析》積分理論的基石，教材[1]先闡述了達(dá)布和的定義和性質(zhì)，在此基礎(chǔ)上證明了定積分存在的第一和第二充要條件。我在教學(xué)中利用定積分存在的兩個(gè)充要條件歸納總結(jié)了Riemann函數(shù)的一些性質(zhì)，在此基礎(chǔ)上精心創(chuàng)設(shè)具有探究性、開(kāi)放性的問(wèn)題情境，讓學(xué)生產(chǎn)生必要的認(rèn)知沖突，有效調(diào)動(dòng)學(xué)生積極思維，主動(dòng)參與認(rèn)知的發(fā)現(xiàn)過(guò)程，引導(dǎo)學(xué)生不斷提出問(wèn)題，澄清了一些錯(cuò)誤理解，證明了R可積函數(shù)類(lèi)的一些深刻性質(zhì)，為學(xué)生學(xué)習(xí)廣義積分、重積分、復(fù)積分和實(shí)分析打下了基礎(chǔ)。

二、教學(xué)設(shè)計(jì)

1．利用復(fù)習(xí)環(huán)節(jié)作好鋪墊。

從宏觀上分析定積分存在的第一和第二充要條件的內(nèi)在聯(lián)系，闡述第一充要條件與第二充要條件的應(yīng)用方法，為Riemann函數(shù)R可積的證明作準(zhǔn)備。

復(fù)習(xí)：

幾個(gè)記號(hào)：

分劃：

（1）復(fù)述定積分存在的兩個(gè)充要條件。

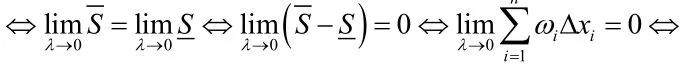
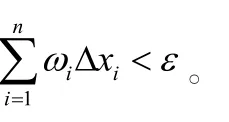
推論1 有界函數(shù)f(x)在[a,b]上R可積的充分必要條件是：對(duì)?ε＞0，存在分劃Δ，

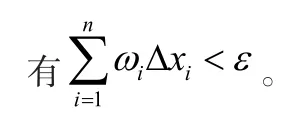
定理2（定積分存在的第二充分必要條件）有界函數(shù)f(x)在[a,b]上R可積的充分必要條件是：對(duì)任意給定的兩個(gè)正數(shù)ε＞0及σ＞0，可找到δ＞0，使得當(dāng)任一分法滿足λ(Δ)＜δ時(shí)，對(duì)應(yīng)于振幅ωi'≥ε的那些區(qū)間Δxi'的長(zhǎng)度之和∑Δxi'＜σ。

推論2 有界函數(shù)f(x)在[a,b]上R可積i'的充分必要條件是：對(duì)任意給定的兩個(gè)正數(shù)ε＞0及σ＞0，存在一分法Δ，對(duì)應(yīng)于振幅ωi'≥ε的那些區(qū)間Δxi'的長(zhǎng)度之和Δxi'＜σ。

（2）這兩個(gè)充要條件之間有何內(nèi)在聯(lián)系？

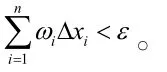
（3）如何應(yīng)用這兩個(gè)充要條件討論函數(shù)的可積性？

證明所有ωi一致小于ε，如連續(xù)函數(shù)可積性的證明；

推論3：若f(x)在[a,b]上連續(xù)，則對(duì)?ε＞0,總可在[a,b]上插入若干分點(diǎn)，使得f(x)在每個(gè)小區(qū)間上的幅度ωi＜ε。

證明n所有Δxi一致小于ε，如單調(diào)有界函數(shù)的可積性的證明；

將∑i=1ωiΔxi分成兩部分，一部分ωi能一致小于ε，另一部分雖然ωi不能一致小于ε，但其區(qū)間長(zhǎng)度的和能一致地小于σ，如只有有限個(gè)不連續(xù)點(diǎn)的有界函數(shù)的可積性的證明。

推論4：若f(x)在[a,b]上R可積，且積分值為I，又f?(x)是f(x)在有限個(gè)點(diǎn)改變函數(shù)值后得到的函數(shù)，則f?(x)在[a,b]上也R可積，且積分值仍為I。

2．改變教材的呈現(xiàn)方式，將命題分解為若干個(gè)前后呼應(yīng)，環(huán)環(huán)相扣的小問(wèn)題，把教材冰冷的美麗變?yōu)閷W(xué)生火熱的思考。

例。定義Riemann函數(shù)

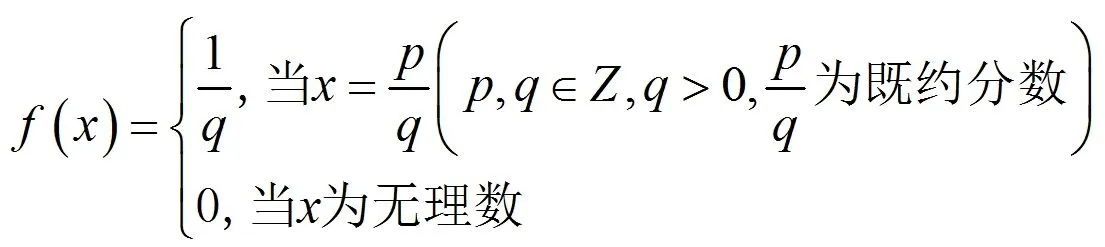
證明：

（1）對(duì)ε＞0，在任意有限區(qū)間[a,b]上使f(x)≥ε的點(diǎn)x只有有限多個(gè)。

（2）f(x)在任意一點(diǎn)的極限都為0。

（3）f(x)在所有無(wú)理點(diǎn)處連續(xù)，有理點(diǎn)處不連續(xù)。

（4）f(x)在任意有限區(qū)間[a,b]上都R可積，且積分值為0。

（5）f(x)沒(méi)有原函數(shù)，從而R可積函數(shù)不一定有原函數(shù)。

3．巧妙設(shè)問(wèn)，層層深化，引導(dǎo)學(xué)生深入思考，領(lǐng)略積分世界的新天地。

接上文，問(wèn)：什么樣的函數(shù)會(huì)沒(méi)有原函數(shù)呢？

（6）含有第一類(lèi)間斷點(diǎn)的函數(shù)一定沒(méi)有原函數(shù)。問(wèn)：知道了f(x)的原函數(shù)是F(x)之后，

引導(dǎo)學(xué)生發(fā)現(xiàn)：上式左邊積分不一定存在。這是因?yàn)?/p>

（7）有原函數(shù)的函數(shù)不一定R可積。

從而f(x)在含有0的區(qū)間[a,b]上無(wú)界，從而在[a,b]上不R可積。

問(wèn)：我們知道含有第一類(lèi)間斷點(diǎn)的函數(shù)一定沒(méi)有原函數(shù)，那么含有第二類(lèi)間斷點(diǎn)的函數(shù)是不是也一定沒(méi)有原函數(shù)呢？

引導(dǎo)學(xué)生發(fā)現(xiàn)，由上例可知：

（8）含有第二類(lèi)間斷點(diǎn)的函數(shù)可以有原函數(shù)。

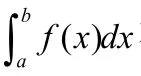
引導(dǎo)學(xué)生發(fā)現(xiàn)，此時(shí)不能套用牛頓-萊布尼茲公式，因?yàn)榕ｎD-萊布尼茲公式的條件是f(x)連續(xù)，但是牛頓-萊布尼茲公式可以推廣為：

（9）若f(x)有原函數(shù)F(x)，且在[a,b]上R可積，

問(wèn)：什么樣的函數(shù)既有原函數(shù)又R可積呢？

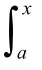
問(wèn)：只有有限個(gè)間斷點(diǎn)的有界函數(shù)是R可積的，那么有無(wú)限個(gè)間斷點(diǎn)的有界函數(shù)R可積嗎？

引導(dǎo)學(xué)生由Riemann函數(shù)和Dirichlet函數(shù)不難發(fā)現(xiàn)：

（11）在[a,b]上有無(wú)限個(gè)間斷點(diǎn)的有界函數(shù)可能R可積，也可能不R可積。

問(wèn)：在[a,b]上有無(wú)限個(gè)間斷點(diǎn)的有界函數(shù)在什么條件下會(huì)一定R可積呢？

（12）若在[a,b]上的有界函數(shù)有無(wú)窮多個(gè)間斷點(diǎn)，但這無(wú)窮多個(gè)間斷點(diǎn)只有唯一的聚點(diǎn)，則該函數(shù)在[a,b]上R可積。

問(wèn)：若在[a,b]上的有界函數(shù)有無(wú)窮多個(gè)間斷點(diǎn)，但這無(wú)窮多個(gè)間斷點(diǎn)有有限個(gè)聚點(diǎn)，則該函數(shù)在[a,b]上R可積嗎？

引導(dǎo)學(xué)生發(fā)現(xiàn)，由積分的區(qū)間可加性可知：

（13）若在[a,b]上的有界函數(shù)有無(wú)窮多個(gè)間斷點(diǎn)，但這無(wú)窮多個(gè)間斷點(diǎn)只有有限個(gè)聚點(diǎn)，則該函數(shù)在[a,b]上R可積。

問(wèn)：若在[a,b]上的有界函數(shù)有無(wú)窮多個(gè)間斷點(diǎn)，但這無(wú)窮多個(gè)間斷點(diǎn)有無(wú)窮個(gè)聚點(diǎn)，則該函數(shù)在[a,b]上R可積嗎？

引導(dǎo)學(xué)生由Riemann函數(shù)和Dirichlet函數(shù)可知

（14）若在[a,b]上的有界函數(shù)有無(wú)窮多個(gè)間斷點(diǎn)，但這無(wú)窮多個(gè)間斷點(diǎn)有無(wú)窮個(gè)聚點(diǎn)，則該函數(shù)在[a,b]上未必R可積。

4．引導(dǎo)學(xué)生對(duì)以上有關(guān)結(jié)論給出嚴(yán)格證明。證明追求嚴(yán)謹(jǐn)，但不拒絕形象直觀。結(jié)合圖形闡述有關(guān)證明思路，從而使推理深入淺出。

5．構(gòu)造具體實(shí)例，幫助學(xué)生理解上述相關(guān)結(jié)論。

例 判斷下列函數(shù)在[0,1]上是否R可積。

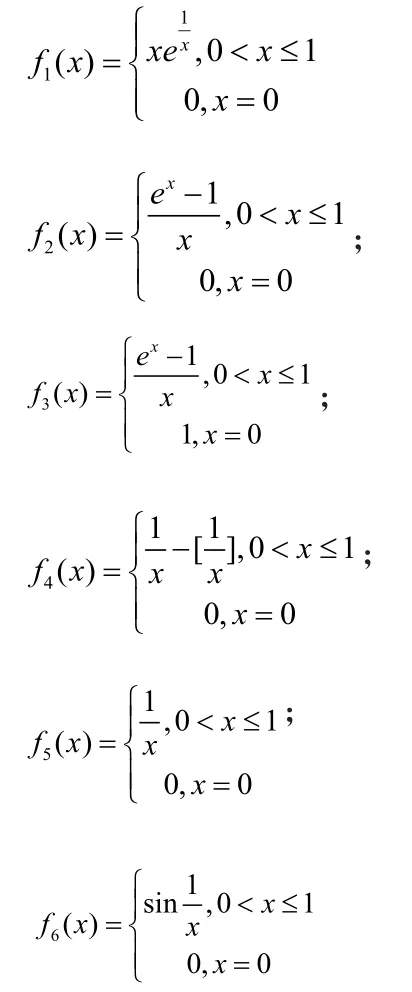
在引導(dǎo)學(xué)生思考“從間斷點(diǎn)的多少的角度看，在[a,b]上的有界函數(shù)R可積有何充要條件？”的問(wèn)題時(shí)，可告訴學(xué)生：實(shí)變函數(shù)理論告訴我們

6．適當(dāng)拓展，激發(fā)學(xué)生的求知欲。

設(shè)f(x)在[a,b]有界，則f(x)在[a,b]上R可積的充要條件是f(x)在[a,b]幾乎處處連續(xù)，即f(x)在[a,b]的間斷點(diǎn)構(gòu)成零測(cè)度集，形象地說(shuō)，其間斷點(diǎn)不“很多”。

又如：Dirichlet函數(shù)在[a,b]上不R可積，但改變積分的定義方式，如在勒貝格積分的意義下它又是可積的，此時(shí)稱(chēng)L可積。

結(jié)語(yǔ)

從Riemann函數(shù)的幾個(gè)常用結(jié)論出發(fā)，精心設(shè)計(jì)了一系列環(huán)環(huán)相扣的問(wèn)題情境，引導(dǎo)學(xué)生始終處于問(wèn)題的探索與求真的過(guò)程中，證明與反例相結(jié)合，幫助學(xué)生厘清了一此似是而非的錯(cuò)誤理解，將對(duì)定積分的理解上升到一個(gè)新的高度。更重要的是，學(xué)生在積極參與知識(shí)的探索過(guò)程中培養(yǎng)了發(fā)現(xiàn)問(wèn)題、提出問(wèn)題的可貴的科學(xué)品質(zhì)和創(chuàng)新精神。