p-進域上的譜和tiling集的一個刻畫

買買提艾力喀迪爾

(喀什大學數學與統計學院,新疆喀什 844006)

1 引言

設G是一個局部緊的Abel群,是其共軛群.假設??G具有正有限Haar測度的Borel可測集合,稱?是一個譜集如果存在G的一個連續特征的集合Λ?,使得組成平方Haar-可積可積函數空間L2(?)的一個正交基.集合Λ稱為?的一個譜,(?,Λ)稱為譜對.我們說一個集合?平移地tileG,如果存在一個集合T?G使得集族{?+t}t∈T構成G的一個劃分(除了零測集外).該集合T稱為?的一個tiling集或者一個平移集,(?,T)稱為一個tiling對.

當G=Rd時,關于譜集和tile的關系Fuglede[1]提出如下的猜想.

譜集猜想一個具有正有限Lebesgue測度的Borel集??Rd是一個譜集當且僅當它是一個平移tile.即存在一個集合Λ使得(?,Λ)是一個譜對當且僅當存在一個集合T使得(?,T)是一個tiling對.

在任何局部緊的Able群G上可以考慮廣義Fuglede猜想:一個正有限Haar測度的Borel集??G是譜集當且僅當它是一個平移tile.甚至在有限群上也可以討論該猜想[2].

我們可以考慮如下的對偶譜集猜想:設Λ?G,則Λ是一個譜當且僅當Λ一個tiling集.即存在一個集合?使得(?,Λ)是一個譜對當且僅當存在一個集合?0使得(?0,Λ)是一個tiling對.

在歐式空間Rd對于這一譜集猜想的研究取得了一些局部性的結果(見文獻[1,3,4]).譜集猜想提出來30年以后,直到2004年菲爾茲獎得主陶哲軒[5]在維數大于等于5的時候構造了一個反例說明譜集未必是tile.現在這些反例的維數降低到d≥3[6,7].至今,譜集猜想在一維或者二維空間上是否成立仍然是一個公開問題.

另一方面,文獻[8]研究了Rd上的單位正方形的所有譜的結構,文獻[9,10]證明了R上的譜集的譜一定是周期的.

最近,范愛華[11]考慮局部域上的譜集和譜測度問題;本文作者[12]證得當譜或者tiling集是擬格的時候譜集猜想在局部域上的向量空間上成立.譜集猜想在p-進域Qp上完全被解決了.其實,他們[13,14]證得一個有界集??Qp是譜集??是一個tile??是幾乎緊開“p-齊次”.同時,他們也證明了Qp上的譜或者tiling集在等距同構的意義下是惟一的.不過,該猜想在上仍然是個公開問題.

2 預備知識

這一部分介紹p-進數域Qp的有關知識,可積函數空間上的Fourier變換,上的譜集準則等相關內容.

2.1 p-進數域Qp

我們首先回顧一下p-進數域.設p≥2是一個素數,Q是有理數域.任何一個非零數x∈Q可以寫成,其中v,a,b∈Z,(p,a)=1和(p,b)=1(這里(x,y)表示兩個整數x和y的最大公因數).根據Z上的唯一分解定理,這個數v只依賴于x.對于定義vp(x)=v,vp(0)=+∞并且,那么|·|p是一個非阿基米德絕對值.即

(i)|x|p≥0,等于零僅當x=0;

(ii)|xy|p=|x|p|y|p;

(iii)|x+y|p≤max{|x|p,|y|p}.

p-進數域Qp是有理數域Q在p-進絕對值|·|p之下的完備化.事實上,Qp的任何一個元素x都可以寫成

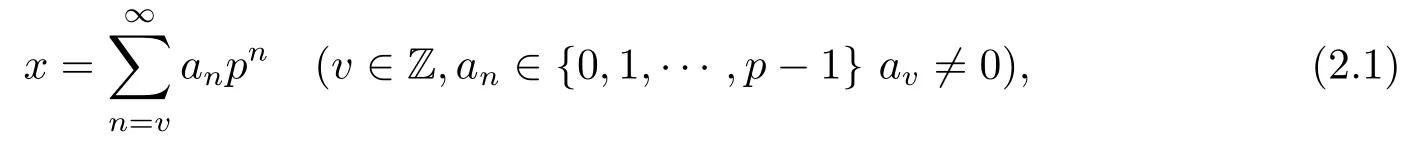
這里v(x):=v稱為x的p-賦值,并且|x|p=p?v.記進整數環,其實它是以0為圓心的單位圓.

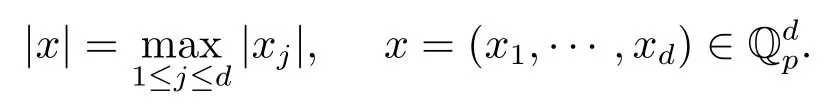
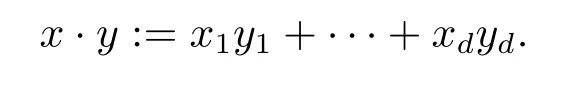
2.2 Fourier變換

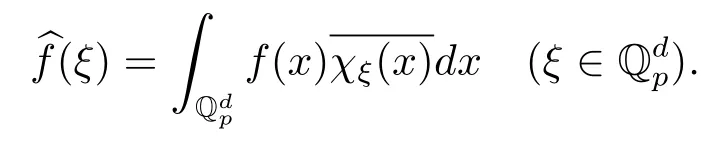
注意

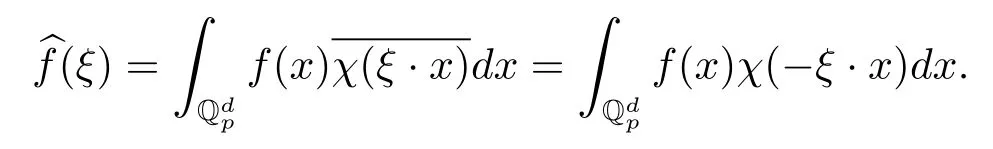
Fourier變換具有如下性質

定義2.1定義在上的一個復值函數f稱為一致局部常值函數,若存在n∈Z使得

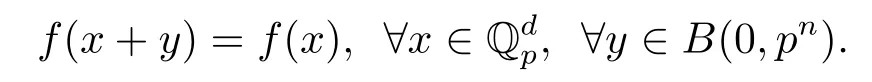
顯然一致局部常值函數是連續的.

用|?|表示集合?的Haar測度.對于一個Borel集使得0<|?|<∞,有下面的譜集準則[11].

引理2.2[11]一個Borel集使得0<|?|<∞是一個以Λ為譜的譜集當且僅當

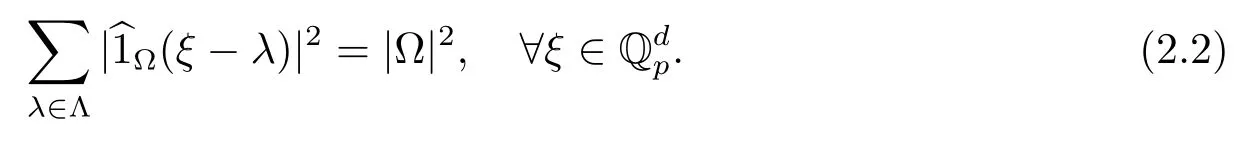
下面的引理確定一個正交集E(Λ)中的點應該滿足的條件.

引理2.3如果是一個Borel集并且0<|?|<∞,那么集合E(Λ)在L2(?)內正交當且僅當

若式(2.3)成立,則對任意Λ,有hχλ,χλ0i?=0,說明E(Λ)是一個正交集.反過來,若E(Λ)在空間L2(?)內的一個正交集,則對任意Λ,有,這個等價于式(2.3).

引理2.4[14]假設是一個Borel集使得0<|?|<∞.

(1)若(?,Λ)是一個譜對,則Λ是一致離散集合.

(2)若(?,T)是一個tiling對,則T是一致離散集合.

取

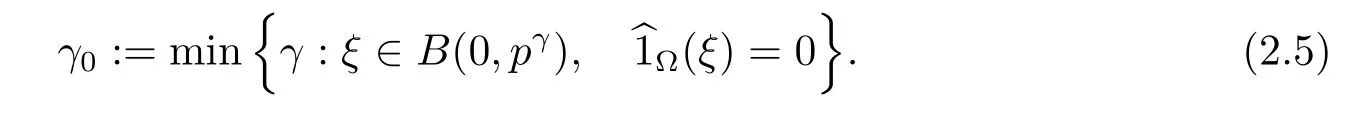
那么引理2.4表示,如果Λ是集合?的一個譜則它是一致離散的并且其分離常數δ(Λ)≥γ0.

3 主要定理及其證明

這一節將介紹主要定理及其證明.

3.1 集合序列的弱收斂

定義3.1設是一個一致離散集合序列,其分裂常數是δ(Λn)≥δ0.集合序列Λn若收斂于一個集合Λ,若對任意η∈N和任意γ∈Z,存在一個自然數N使得對任意n≥N,有

其中Bγ是以原點為球心,以pγ為半徑的開球.這個時候極限Λ也是一致離散,并且δ(Λ)≥δ0.

下面的定理是本文的主要結果.

定理3.2設是一個一致離散集合序列,分裂常數是δ(Λn)≥δ0,并且弱收斂于一個集合Λ.假設是一個有界可測集合,并且對任意n,Λn是?的一個譜(或tiling集),那么Λ也是?的一個譜(或tiling集).

下面介紹這個定理的證明所需要的一系列引理.

3.2 函數tiling

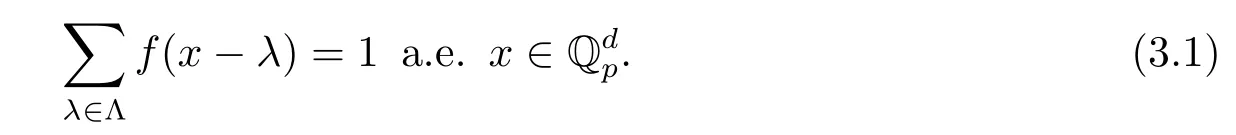
這種情況下,寫f+Λ是一個tiling.

如果f=1?是一個有界可測集合的示性函數,那么條件(3.1)表示集族{?+λ:λ∈Λ}構成的一個劃分(除零測集外).這個時候函數tiling就是集合tiling,并且我們說(?,Λ)是一個tiling對.

下面的引理給出通過tiling條件來刻畫集合?的譜的一個方法.

引理3.3假設是一個有界可測集合,定義

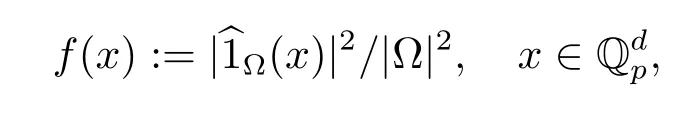
證由于引理2.2,我們有(?,Λ)是譜對當且僅當對任意,有

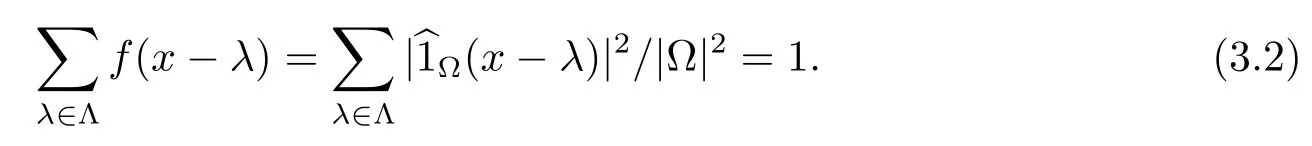
方程(3.2)成立當且僅當f+Λ是一個tiling.

3.3 正交性與填充

這種情況下,寫f+Λ是一個填充.注意如果f=1?,那么這個表明集族{?+λ:λ∈Λ}是兩兩測度不交.這個時候,我們說(?,Λ)是一個填充對.

假設E,F是上的兩個離散集合,τ是是的一個向量.設三個集合F,F+τ,F?τ的每一個與集合集合E不交,并且定義

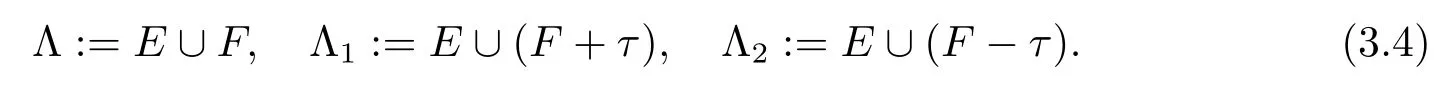
引理3.4令f≥0是上的一個可測函數.假設f+Λ是一個tiling,f+Λ1和f+Λ2是填充,那么f+Λ1和f+Λ2也是tilings.

證定義

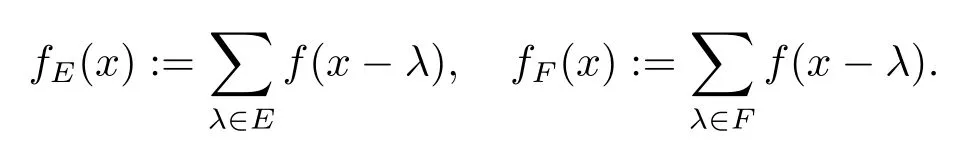
(1)fE(x)+fF(x)=1.

(2)fE(x)+fF(x?τ)≤1.

(3)fE(x)+fF(x+τ)≤1.

分別從(2)和(3)減去(1)得到

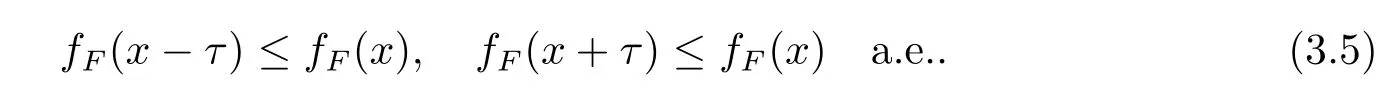
通過向量τ平移可知,式(3.5)成立等價于fF(x?τ)=fF(x)=fF(x+τ).這個隱含著引理成立.

引理3.5一個指數函數系E(Λ)在空間L2(?)內正交當且僅當f+Λ是一個填充,其中.

這個引理的證明完全類似于引理3.3的證明.

運用引理3.3,引理3.4和引理3.5得到

推論3.6假設Λ,Λ1,Λ2是定義在式(3.4),若集合Λ是?的一個譜,集族E(Λ1)和E(Λ2)在空間L2(?)內正交,則集合Λ1和Λ2也是?的譜.

定理3.7設是一個一致離散集合序列,分裂常數是δ(Λn)≥δ0,并且弱收斂于一個集合Λ.假設,并且對任意n,f+Λn是一個tiling,那么f+Λ也是一個tiling.

證假設函數ψ≥0是上的具有緊支撐的局部常值函數并且滿足.那么證明對于這種函數ψ如下等式

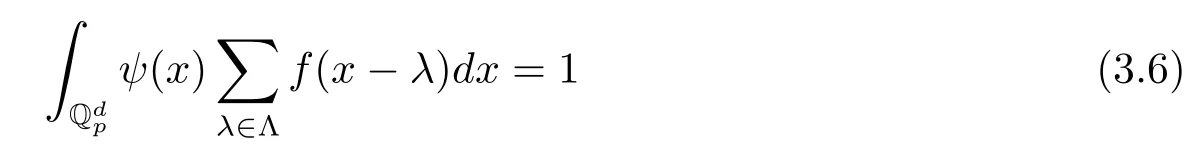
成立就可以了.

固定一個滿足上述條件的函數ψ,定義

由于Λn弱收斂于Λ,所以對任何上的具有緊支撐的局部常值函數?,有

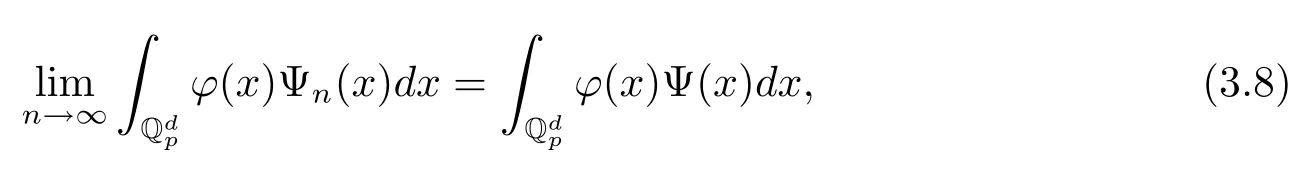
下面給予定理3.2的證明.

定理3.2的證明設是一個有界可測集合.令f(x):=1?(x),則,f≥0.根據定理3.7,若對于任意n,?+Λn是一個tiling,并且Λn弱收斂于Λ,則?+Λ也是一個tiling.