基于超聲導(dǎo)波的管道缺陷量化評(píng)估仿真研究

梁伯翱,趙 鍇,王曉娟,陳曉曉

(西安理工大學(xué)機(jī)械與精密儀器工程學(xué)院,陜西西安710048)

超聲導(dǎo)波[1]是近年來(lái)新興的無(wú)損檢測(cè)技術(shù)。相對(duì)于傳統(tǒng)的無(wú)損檢測(cè)方法,它具有以下優(yōu)勢(shì):①傳播距離遠(yuǎn),超聲導(dǎo)波在固體中傳播時(shí)沿傳播路徑上的衰減很小,可以在管道內(nèi)傳播很遠(yuǎn)的距離,最遠(yuǎn)可達(dá)上百米;②檢測(cè)效率高,超聲導(dǎo)波是線性檢測(cè),不是傳統(tǒng)檢測(cè)的點(diǎn)對(duì)點(diǎn)檢測(cè),大大提高了效率;③檢測(cè)范圍廣,超聲導(dǎo)波在管道的內(nèi)、外表面和中部都有振動(dòng)的質(zhì)點(diǎn),聲場(chǎng)遍及整個(gè)壁厚,因此整個(gè)壁厚都可以檢測(cè)到。早在上個(gè)世紀(jì)中期,外國(guó)學(xué)者已經(jīng)開始對(duì)聲波在管道中的傳播進(jìn)行理論研究。上世紀(jì)80年代,Silk和Bainton[2]利用壓電超聲傳感器激勵(lì)出超聲導(dǎo)波,對(duì)電機(jī)管道的裂紋檢測(cè)進(jìn)行了實(shí)驗(yàn),證明了利用超聲導(dǎo)波技術(shù)檢測(cè)管道的可能性。近些年,國(guó)內(nèi)外的學(xué)者也開展了相關(guān)的實(shí)用化研究。何存富[3]開發(fā)出一種集成化的小型超聲導(dǎo)波檢測(cè)系統(tǒng),該系統(tǒng)能夠在管道中激勵(lì)和接收超聲導(dǎo)波,并通過(guò)對(duì)激勵(lì)及反射回波的時(shí)空位置分析判斷出管道長(zhǎng)度和存在的缺陷。王智[4]重點(diǎn)研究了采用分布式PZT傳感器在管中激勵(lì)和接收特定模態(tài)超聲導(dǎo)波的方法,并在此基礎(chǔ)進(jìn)一步研究管道缺陷回波的特性,通過(guò)分析、處理接收到的管道中的缺陷回波特征,達(dá)到缺陷識(shí)別和定位的目的。宋志東[5]分析了管道中的超聲導(dǎo)波在傳播過(guò)程中的衰減特性和缺陷反射特性,并通過(guò)L(0,2)模態(tài)和T(0,1)模態(tài)對(duì)含缺陷管道進(jìn)行檢測(cè),指出縱向模態(tài)和扭轉(zhuǎn)模態(tài)導(dǎo)波檢可提供全部缺陷特征,并可以較為準(zhǔn)確地對(duì)缺陷定位。

這些研究表明超聲導(dǎo)波檢測(cè)已經(jīng)實(shí)現(xiàn)了對(duì)管道缺陷的識(shí)別和對(duì)缺陷的定位。但由于實(shí)際管道缺陷形態(tài)不規(guī)則,產(chǎn)生的反射回波信號(hào)往往很復(fù)雜,目前還不能實(shí)現(xiàn)管道缺陷的量化評(píng)估。本文針對(duì)此問(wèn)題,通過(guò)有限元仿真方法研究超聲導(dǎo)波與管道缺陷的交互過(guò)程,提出裂紋缺陷軸向尺寸的研究方法,提出利用缺陷前后沿分別產(chǎn)生的兩個(gè)邊界反射信號(hào)進(jìn)行缺陷軸向尺寸的量化評(píng)估方法,并進(jìn)一步通過(guò)有限元仿真驗(yàn)證了結(jié)論。

1 管道超聲導(dǎo)波的有限元仿真

1.1 超聲導(dǎo)波基礎(chǔ)理論

波在管道中傳播時(shí),滿足Navier運(yùn)動(dòng)方程[6]:

μ2u+(λ+μ)(

(1)

式中:μ和λ是管道材料的Lame常數(shù),ρ是管道材料密度,u是位移場(chǎng)。

根據(jù)波動(dòng)方程可進(jìn)一步得到管道的頻散方程,即與管道的內(nèi)外徑、密度、頻率及波數(shù)有關(guān)的函數(shù)。頻散方程的三種解對(duì)應(yīng)導(dǎo)波的三種模態(tài):縱向模態(tài)、扭轉(zhuǎn)模態(tài)和彎曲模態(tài),分別用L(m,n)、T(m,n)和F(m,n)表示,其中m和n分別表示周向和軸向模態(tài)參數(shù),且均為整數(shù)。縱向模態(tài)和扭轉(zhuǎn)模態(tài)為對(duì)稱模態(tài),彎曲模態(tài)為非對(duì)稱模態(tài)。其中,縱向?qū)Р↙(0,2)模態(tài)是所有模態(tài)中速度最快的,在管道檢測(cè)時(shí)它能更快的到達(dá)接收端,因而可以更好地與其他模態(tài)進(jìn)行區(qū)分,且L(0,2)模態(tài)在高頻時(shí),波速變化不大,頻散現(xiàn)象不明顯,這就使其在傳播過(guò)程中衰減很小,可以到達(dá)更遠(yuǎn)的距離,同時(shí)波形圖的幅值更大。另外,導(dǎo)波L(0,2)模態(tài)軸向位移相對(duì)較大,而周向位移分量相對(duì)較小,且位移分布相對(duì)均勻,所以L(0,2)模態(tài)導(dǎo)波對(duì)管道內(nèi)外有一樣的靈敏度。而T(0,1)模態(tài)傳播速度保持恒定,無(wú)頻散現(xiàn)象。這兩種模態(tài)各有特點(diǎn),在基于超聲導(dǎo)波的管道檢測(cè)應(yīng)用中會(huì)根據(jù)檢測(cè)需求考慮選擇激勵(lì)L或T模態(tài),本文選擇L(0,2)模態(tài)作為激勵(lì)導(dǎo)波。

基于超聲導(dǎo)波的管道缺陷檢測(cè)過(guò)程見圖1:通過(guò)交變電信號(hào)驅(qū)動(dòng)壓電陶瓷換能片,壓電陶瓷由于逆壓電效應(yīng)發(fā)生機(jī)械形變從而在所處管道上產(chǎn)生機(jī)械波。這種機(jī)械波在管道內(nèi)以導(dǎo)波形式傳播,根據(jù)應(yīng)力波理論,導(dǎo)波在遇到缺陷會(huì)發(fā)生反射、折射等現(xiàn)象并伴隨模態(tài)轉(zhuǎn)換,由接收端陶瓷壓電換能片接收回波信號(hào)。在導(dǎo)波速度等信息已知的情況下,可通過(guò)分析回波信號(hào)實(shí)現(xiàn)對(duì)缺陷的檢測(cè)與評(píng)估。

圖1 超聲導(dǎo)波傳播示意圖Fig.1 Illustration of guided waves propagating in pipeline

1.2 管道缺陷檢測(cè)有限元仿真

有限元仿真分析主要包括三個(gè)過(guò)程[7]:前處理,求解計(jì)算和后處理。其中前處理主要是為求解計(jì)算提供準(zhǔn)備工作,涉及到的操作包括定義分析類型、定義單元類型、設(shè)置屬性參數(shù)、建立管道幾何模型,并對(duì)建立的管道模型進(jìn)行網(wǎng)格劃分。求解計(jì)算主要包括施加邊界條件、施加脈沖載荷、設(shè)置求解分析類型、確定載荷時(shí)間和載荷子步,并進(jìn)行求解。后處理主要是從選取相關(guān)節(jié)點(diǎn)得到其位移時(shí)間關(guān)系,并進(jìn)一步通過(guò)信號(hào)波形確定檢測(cè)所需的相關(guān)信息。

研究超聲導(dǎo)波和管道缺陷交互作用的有限元建模及分析的基本流程圖見圖2。

圖2 管道缺陷檢測(cè)有限元仿真流程圖Fig.2 Flow chart of FE simulation of pipe defect inspection

1.3 有限元模型的建立及參數(shù)設(shè)置

本文分析討論所用的管道有限元模型具體數(shù)據(jù)為:管道長(zhǎng)度1 m,壁厚4 mm;缺陷距離管道端部0.5 m,徑向深2 mm,周向?qū)?60°,軸向長(zhǎng)度在3 mm到180 mm范圍內(nèi)變化。管道模型的材料特性參數(shù)見表1。

表1 管道模型的材料特性參數(shù)Tab.1 Parameters of material property for FE pipe model

本文分析討論的管道模型的頻散曲線見圖3,由英國(guó)帝國(guó)理工大學(xué)開發(fā)的Disperse軟件繪制。由式(2)可得L(0,2)模態(tài)導(dǎo)波的理論波速為5 288 m/s。

(2)

式中:E為彈性模量,ρ為密度,ν為泊松比。

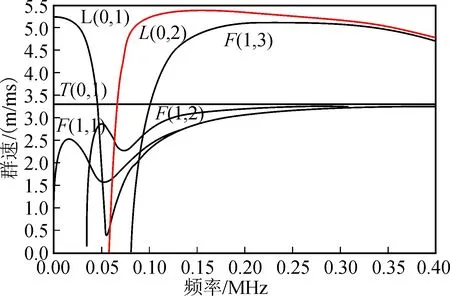
圖3 本文管道模型的頻散曲線圖Fig.3 Dispersion curve of pipe model used in the paper

網(wǎng)格的劃分和時(shí)間子步的選擇是有限元模型建立的關(guān)鍵。對(duì)管道模型進(jìn)行網(wǎng)格劃分[8]須滿足以下幾個(gè)條件:軸向單元的長(zhǎng)度小于激發(fā)信號(hào)波長(zhǎng)λ的十分之一;端面網(wǎng)格劃分與檢測(cè)系統(tǒng)中傳感器的周向分布一致或是其整倍數(shù);此外,網(wǎng)格劃分應(yīng)保證計(jì)算精度滿足要求而同時(shí)盡可能減少計(jì)算量。因此,根據(jù)本文建立的管道有限元模型的參數(shù),選擇網(wǎng)格劃分單元類型為SOLID185,軸向單元長(zhǎng)度2 mm,以保證仿真結(jié)果趨于穩(wěn)定。

同時(shí),總的仿真計(jì)算時(shí)間T須滿足接收端至少接受到一次完整的導(dǎo)波反射信號(hào):

(3)

式中,L為管道長(zhǎng)度,Vg為導(dǎo)波在管道中傳播的群速度。

時(shí)間子步ΔT必須滿足:

(4)

式中,le是軸向單元長(zhǎng)度。

管道模型的仿真參數(shù)見表2。

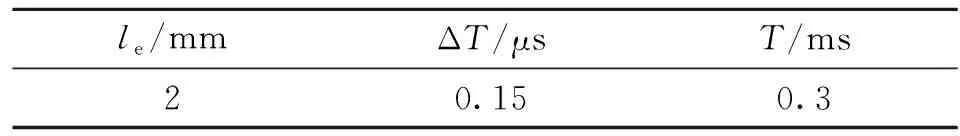
表2 管道模型的仿真參數(shù)設(shè)定Tab.2 Simulation parameter setting of FE pipe model

建立的有限元仿真模型見圖4,由此模型得到的缺陷反射回波信號(hào)見圖5。

本文討論的仿真模型激勵(lì)信號(hào)為L(zhǎng)(0,2)模態(tài),實(shí)際從缺陷產(chǎn)生的模態(tài)包括L(0,2)和L(0,1)模態(tài)。L(0,1)模態(tài)相比L(0,2)模態(tài)能量小且速度慢,因此下文只討論分析主模態(tài)L(0,2)對(duì)應(yīng)的缺陷回波。

圖4 含缺陷管道的有限元仿真模型Fig.4 FE simulation model of pipe with a defect

圖5 仿真模型缺陷反射回波信號(hào)Fig.5 Defect reflectoin signal of simulation model

2 管道缺陷軸向長(zhǎng)度的量化評(píng)估

為研究管道缺陷的量化評(píng)估,首先通過(guò)有限元仿真方法研究超聲導(dǎo)波與管道缺陷的交互過(guò)程。本文重點(diǎn)考慮缺陷軸向長(zhǎng)度,因此仿真研究的缺陷模型的三維尺寸中,徑向深度和周向?qū)挾缺３植蛔?僅軸向長(zhǎng)度變化。

仿真研究的結(jié)果發(fā)現(xiàn),隨著缺陷軸向距離的增大,回波信號(hào)逐漸分離(見圖6)。在缺陷軸向長(zhǎng)度為3 mm時(shí),反射回波的波形與激勵(lì)波形幾乎相同,只是幅值產(chǎn)生減小;當(dāng)缺陷軸向長(zhǎng)度增大為3 cm、6 cm時(shí),反射回波的包絡(luò)線明顯變寬;而增大至9 cm時(shí),反射回波的波形逐漸分開為兩個(gè)獨(dú)立的波包,且波形與激勵(lì)波形近似相同;至12 cm時(shí),反射回波完全分離為兩個(gè)波包。同時(shí),在6 cm之后反射回波的兩個(gè)波形基本分開。反射回波的第一個(gè)波包幅值不再變化,其形狀保持一致;而第二個(gè)波包與第一個(gè)波包時(shí)間間隔逐漸增大,其幅值均小于前者,且呈現(xiàn)周期性變化。

分析可判斷缺陷反射回波中包含的兩個(gè)波包分別由缺陷的前后邊界產(chǎn)生。當(dāng)缺陷軸向長(zhǎng)度較小時(shí),前后邊界產(chǎn)生的反射信號(hào)重疊在一起,形成缺陷反射回波;隨著缺陷軸向長(zhǎng)度的增大,前后邊界產(chǎn)生的反射信號(hào)時(shí)間間隔增大,直至完全分離出兩個(gè)波包。我們將前后邊界反射信號(hào)完全分離時(shí)對(duì)應(yīng)的缺陷軸向長(zhǎng)度定義為臨界軸向長(zhǎng)度。前后邊界反射信號(hào)和缺陷反射回波相比,缺陷反射回波模式更復(fù)雜,而邊界反射信號(hào)與激勵(lì)信號(hào)有更強(qiáng)的相關(guān)性,且能提供更多和缺陷尺寸相關(guān)的信息。

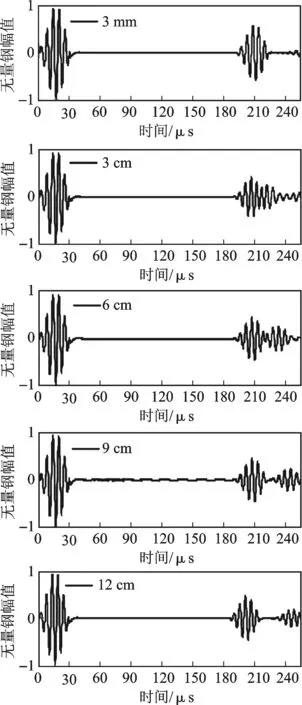
圖6 不同軸向長(zhǎng)度裂紋缺陷的仿真時(shí)程圖Fig.6 Time-distance graph of different axial lengths of pipe defect

如前所述,管道缺陷的量化評(píng)估一直是導(dǎo)波檢測(cè)中需要解決的難題。現(xiàn)有的評(píng)估方法一般都需要利用一定的基準(zhǔn)信號(hào)作為參考實(shí)現(xiàn)缺陷的評(píng)估,且往往只能提供定性的評(píng)估結(jié)果。根據(jù)我們對(duì)超聲導(dǎo)波與管道缺陷的交互過(guò)程的仿真研究結(jié)果,缺陷前后邊界分別產(chǎn)生的反射信號(hào)可提供缺陷前后邊界的對(duì)應(yīng)信息,并進(jìn)一步得到兩邊界間距,即實(shí)現(xiàn)對(duì)缺陷軸向長(zhǎng)度的量化評(píng)估。缺陷軸向長(zhǎng)度的量化評(píng)估主要涉及缺陷軸向定位和缺陷軸向長(zhǎng)度的計(jì)算。

1) 缺陷軸向定位

缺陷定位是缺陷量化的第一步,同時(shí)也是很重要的一步。只有在缺陷定位正確的前提下,缺陷尺寸評(píng)估的研究才有意義。應(yīng)用缺陷前后邊界反射信號(hào)對(duì)缺陷進(jìn)行軸向定位具體是指,通過(guò)導(dǎo)波傳播至缺陷前邊界再返回管道端面的時(shí)間和導(dǎo)波在管道中的傳播速度,求解缺陷距離激勵(lì)傳感器的軸向距離,即實(shí)現(xiàn)缺陷的軸向定位,其示意圖見圖7。缺陷邊界反射回波時(shí)間可由檢測(cè)系統(tǒng)采集信號(hào)直接得到,導(dǎo)波傳播速度可由頻散曲線得到。軸向定位應(yīng)滿足如下公式:

(5)

式中,la是管道端面至缺陷處前沿的距離,tb是導(dǎo)波經(jīng)缺陷前沿第一次返回至端面的時(shí)間,ta是導(dǎo)波在管道端面激勵(lì)出波谷的時(shí)間,v是L(0,2)模態(tài)導(dǎo)波傳播的速度。

圖7 前后邊界反射回波示意圖Fig.7 Reflectoin signal at front and rear boundary

2) 缺陷軸向長(zhǎng)度評(píng)估

利用缺陷前后邊界反射信號(hào)評(píng)估缺陷軸向長(zhǎng)度具體是指,通過(guò)導(dǎo)波分別傳播至缺陷前、后邊界再返回管道端面的時(shí)間和導(dǎo)波在管道中的傳播速度,求解得到缺陷的軸向長(zhǎng)度。軸向長(zhǎng)度計(jì)算應(yīng)滿足下面公式:

(6)

式中,ld是缺陷的軸向長(zhǎng)度,tc是導(dǎo)波經(jīng)缺陷后沿第一次返回至端面的時(shí)間。

一般缺陷軸向長(zhǎng)度的量化可首先通過(guò)理論計(jì)算得到缺陷前后邊界分離的臨界長(zhǎng)度,在此基礎(chǔ)上進(jìn)行前后邊界反射信號(hào)的分離,分離之后對(duì)時(shí)間信息進(jìn)行提取,最后計(jì)算得到缺陷的軸向長(zhǎng)度。

2.1 裂紋缺陷臨界長(zhǎng)度的確定

根據(jù)上文討論,隨著缺陷軸向長(zhǎng)度的增加,前后邊界反射信號(hào)逐漸分開。當(dāng)軸向長(zhǎng)度增大至臨界軸向長(zhǎng)度時(shí),前后沿信號(hào)將完全分開。本文選取的激勵(lì)頻率為175 kHz,選取的激勵(lì)信號(hào)是Hanning窗調(diào)制的5個(gè)周期的單音頻正弦信號(hào)。臨界軸向長(zhǎng)度計(jì)算公式如下所示:

(7)

式中,v是L(0,2)模態(tài)導(dǎo)波的傳播速度,t是周期。管道模型的臨界條件參數(shù)見表3。

表3 管道模型的臨界條件參數(shù)Tab.3 Parameters of critical condition for pipeline FE model

本文所得到的裂紋缺陷臨界長(zhǎng)度為75.76 mm,其導(dǎo)波波形見圖8。

圖8 臨界軸向長(zhǎng)度的時(shí)程圖Fig.8 Time-distance graph of critical axial length

2.2 前后邊界反射信號(hào)的分離

由上文可以知道,任何缺陷的反射回波都包含前后邊界反射信號(hào)的成份。在圖9(b)中可看到,軸向缺陷為10 mm時(shí),前后邊界反射信號(hào)是完全重疊的。如果要分析前后沿信號(hào),首先就要將前后沿信號(hào)完全分離開來(lái),得到單獨(dú)的前后沿信號(hào)。

本文在有限元軟件中分別建立缺陷軸向長(zhǎng)度為10 mm和180 mm管道模型,兩模型除缺陷軸向長(zhǎng)度不同外,其它參數(shù)完全一致,前后邊界反射信號(hào)可通過(guò)以下方法得到。

首先對(duì)軸向長(zhǎng)度為180 mm的缺陷進(jìn)行建模仿真,結(jié)果顯示前后邊界反射信號(hào)是完全分開的。

圖9(a)中的第一個(gè)波包對(duì)應(yīng)前邊界反射信號(hào)f(1)。進(jìn)一步對(duì)軸向長(zhǎng)度為10 mm的缺陷進(jìn)行建模仿真,這種情況下前后邊界反射信號(hào)會(huì)重疊在一起,圖9(b)中的第一個(gè)波包對(duì)應(yīng)前后邊界反射信號(hào)的疊加信號(hào)f(2),即缺陷回波信號(hào)。將信號(hào)f(2)與f(1)比較做差得到信號(hào)f(3),如圖9(c)所示。第一個(gè)波包對(duì)應(yīng)缺陷前邊界反射信號(hào),第二個(gè)波包對(duì)應(yīng)缺陷后邊界反射信號(hào)。

圖9 前后邊界反射信號(hào)分離過(guò)程Fig.9 Separation of front and back boundary signals

2.3 缺陷的軸向長(zhǎng)度驗(yàn)證

圖10為不同軸向長(zhǎng)度缺陷的幅值變化,可以看到,缺陷軸向長(zhǎng)度30 mm時(shí),前沿幅值為0.43,其余前沿幅值均為0.46,說(shuō)明前后邊界反射波包逐漸分離后,前邊界反射信號(hào)幅值能量保持不變,不受缺陷軸向長(zhǎng)度的變化的影響。相對(duì)前邊界反射信號(hào)的穩(wěn)定,缺陷后邊界能量的變化更為復(fù)雜。例如缺陷軸向長(zhǎng)度30 mm時(shí),后邊界反射幅值為0.26,軸向長(zhǎng)度增加至臨界值時(shí),后沿幅值減小0.21,90 mm時(shí),又增大至0.24;120 mm時(shí),又減小0.18,說(shuō)明后沿能量變化的整體趨勢(shì)隨著軸向長(zhǎng)度的增加而減小。同時(shí),可以看出,前沿的幅值均大于后沿的幅值,即超聲導(dǎo)波在管道傳播過(guò)程中,前沿接收的能量更多。

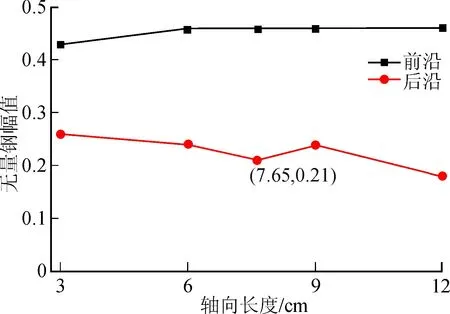
圖10 不同軸向長(zhǎng)度缺陷的幅值變化圖Fig.10 Amplitude change for defects with different axial lengths

不同軸向長(zhǎng)度缺陷的仿真結(jié)果見表4,可以看出,隨著缺陷軸向長(zhǎng)度的增加,超聲導(dǎo)波從激勵(lì)處傳播至缺陷前后邊界的時(shí)間間隔線性增大。仿真試驗(yàn)得出的軸向長(zhǎng)度也越來(lái)越接近理論軸向長(zhǎng)度,當(dāng)理論軸向長(zhǎng)度為10 mm時(shí),仿真試驗(yàn)得出的軸向長(zhǎng)度為11.14 mm,誤差為11.14%,而當(dāng)理論軸向長(zhǎng)度為20 mm時(shí),仿真試驗(yàn)得出的軸向長(zhǎng)度為21.08 mm,誤差為5.41%。繼續(xù)增大理論軸向長(zhǎng)度,所得到的誤差減小至5%以下。當(dāng)理論軸向長(zhǎng)度達(dá)到100 mm時(shí),所得到的誤差為1.03%,精度達(dá)到98.97%。

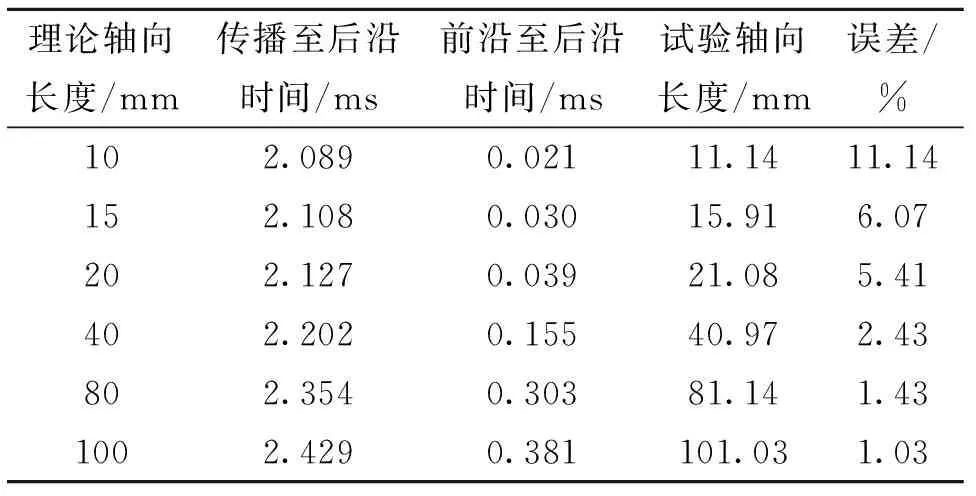
表4 不同軸向長(zhǎng)度缺陷的仿真結(jié)果Tab.4 Simulation results for defects with different axial lengths

3 結(jié) 語(yǔ)

有限元仿真是研究超聲導(dǎo)波的重要手段,本文通過(guò)有限元仿真方法研究超聲導(dǎo)波與管道缺陷的交互過(guò)程,針對(duì)缺陷尺寸的量化評(píng)估問(wèn)題得出了以下結(jié)論。

1) 提出利用缺陷前后邊界反射信號(hào)進(jìn)行缺陷軸向尺寸的量化評(píng)估方法。現(xiàn)有的評(píng)估方法一般都需要利用一定的基準(zhǔn)信號(hào)作為參考實(shí)現(xiàn)缺陷的評(píng)估,且往往只能提供定性的評(píng)估結(jié)果。而根據(jù)缺陷前后邊界分別產(chǎn)生的反射信號(hào)可提供缺陷前后邊界的對(duì)應(yīng)信息,并進(jìn)一步得到兩邊界間距,即實(shí)現(xiàn)對(duì)缺陷軸向長(zhǎng)度的量化評(píng)估。

2) 通過(guò)有限元仿真實(shí)驗(yàn),利用仿真數(shù)據(jù)實(shí)現(xiàn)了從缺陷回波中分離出前后邊界反射信號(hào),驗(yàn)證了本文提出的可利用缺陷前后邊界反射信號(hào)進(jìn)行缺陷軸向長(zhǎng)度量化評(píng)估方法。進(jìn)一步的研究工作可在此基礎(chǔ)上展開,如分離算法的構(gòu)建和邊界反射信號(hào)的進(jìn)一步分析等,以實(shí)現(xiàn)缺陷尺寸的全面量化評(píng)估。