等離子鞘套隨機特性對電波傳播影響分析

劉江凡，李 慧，焦子涵，白光輝，席曉莉

(1.西安理工大學自動化與信息工程學院，陜西西安7100482.中國運載火箭技術研究院 空間物理重點實驗室，北京100076)

高超聲速飛行器在大氣層中飛行時，飛行器與其周圍空氣劇烈摩擦，使空氣分子及飛行器表面材料發生電離，形成等離子鞘套。等離子鞘套的存在，使得投射其上的電磁波產生反射、折射及散射，而在其中傳播的電磁波受到衰減，從而影響飛行器的導航、遙測和通信信號的傳輸，在某些條件下甚至會導致飛行器與衛星和地面的無線電聯系完全中斷，形成黑障效應。

早在20世紀60～90年代，已有學者對再入黑障問題開展了大量理論與試驗研究，取得了許多重要進展[1-6]。總體來看，這些早期的研究主要從無線電頻段選取、電波傳播特性計算、鞘套對天線性能影響以及黑障的削弱技術等方面開展。

近些年來，針對等離子鞘套引起的通信中斷問題的研究，除采用更為完善的電磁數值計算方法，分析計算穩態情況下等離子鞘套中電波傳播特性[7]、鞘套的電磁散射特性[8-9]以及其對天線特性的影響[10-11]外，在研究鞘套中電波傳播特性方面，研究者開始更多地關注再入湍流等離子的隨機變化特性對電波傳播的影響[12-18]。

本文將色散媒質的線性分段遞歸卷積(Piecewise Linear Recursive Convolution， PLRC)FDTD方法[19]與S-FDTD方法結合，提出了S-PLRC-FDTD方法，并采用該方法進一步分析了典型鞘套電子密度分布下，電子密度隨機特性對電波信號影響。

1 等離子體的S-PLRC-FDTD算法

各向同性、碰撞的冷等離子體中，電磁波滿足的Maxwell相關方程和本構方程如下：

(1)

(2)

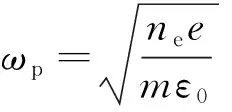
1.1 場量均值的迭代方程

采用FDTD方法計算時，需要將式(2)轉換到時間域，并對其進行離散后得FDTD遞推公式。本文采用色散媒質中常用的PLRC[19-20]方法，得到等離子體中電場的迭代方程。以電場x分量為例，其的迭代方程如下：

(3)

式中C1與C2是與等離子體參數相關的兩個系數，可表示為：

(4)

其中g1=Δt/2υ+a1/υ3Δt,g2=Δt/υ-a2/υ2-g1,a1=-1+(1+υΔt)exp(-υΔt),a2=1-exp(-υΔt)。

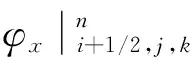
φxn=k1ωp2Exn+k2ωp2Exn-1+

exp(-υΔt)φxn-1

(5)

其中:k1=-a2a1+a2υΔt/υ3Δt，k2=a1a2/

υ3Δt。

磁場的均值迭代方程與普通媒質一致，在此不再贅述。

1.2 場量方差的迭代方程

本小節將推導等離子體中電場及其輔助變量標準差的迭代公式。在推導過程中，仍遵循文獻[16, 18]給出相關準則。

首先推導電場方差的迭代公式，將式(3)兩端同乘(ε+ωp2g2)可以得到：

εEx|n+1+g2ωp2Ex|n+1-ε

(6)

對式(6)左右兩端同時取方差：

σ2εEx|n+1+g2ωp2Ex|n+1-εEx|n+

g1ωp2Ex|n-φx|n=σ2Δt/ε0·

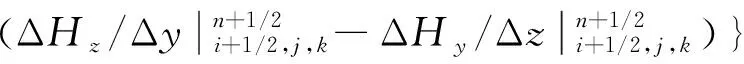
(7)

當相關系數取如下近似時：

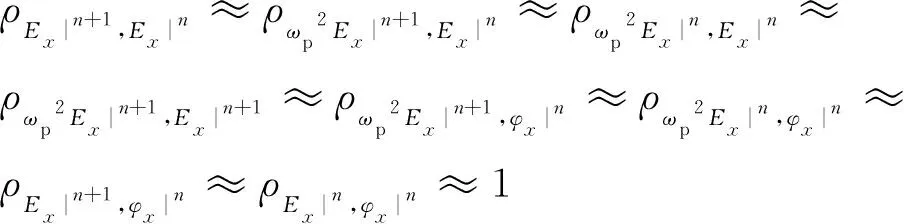
(8)

式(7)可簡化為：

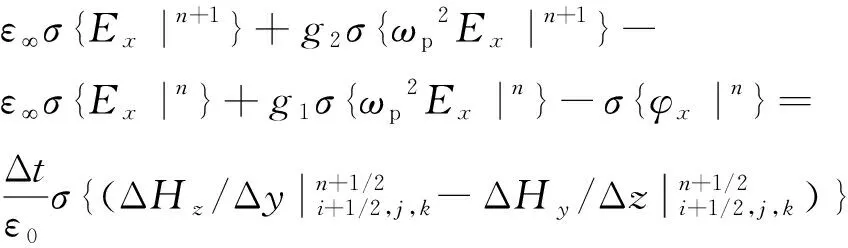
(9)

對式(9)中左端σωp2Ex|n+1和σωp2Ex|n兩項使用delta法[16, 18]進行展開，第一項可以寫為：

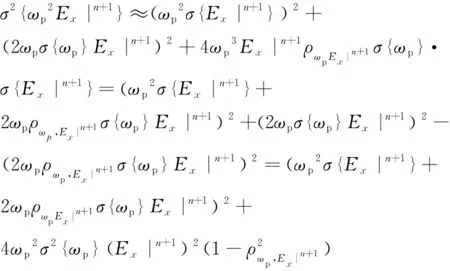
(10)

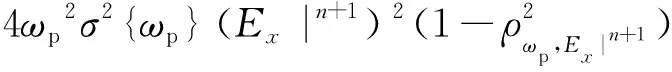
σωp2Ex|n+1≈2ρωp,Ex|n+1ωpEx|n+1σωp+ωp2σEx|n+1

(11)

類似地，σωp2Ex|n項可以化簡為：

σωp2Ex|n≈2ρωp,Ex|nωpEx|nσωp+ωp2σEx|n

(12)

將式(11)～(12)代入式(9)中可以得到σEx|n+1的迭代方程：

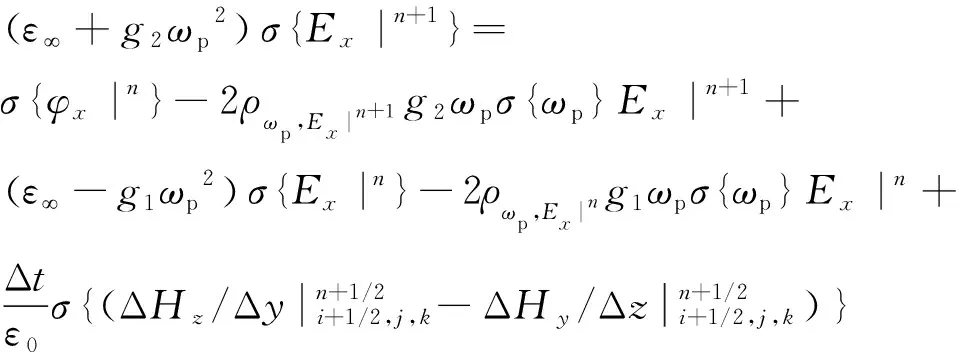
(13)

式(13)即為等離子體中的S-PLRC-FDTD場值方差迭代公式。

接下來我們將進一步推導輔助變量φx的方差迭代公式。對式(5)兩端同時取方差得：

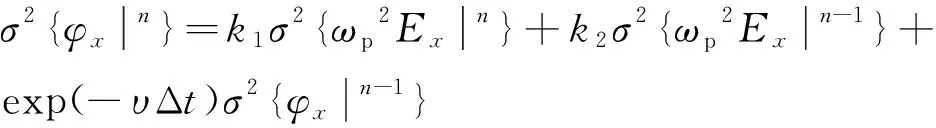
(14)

對式(14)中k1σ2ωp2Exn和k2σ2ωp2Exn-1兩項使用delta法[18]，可得：

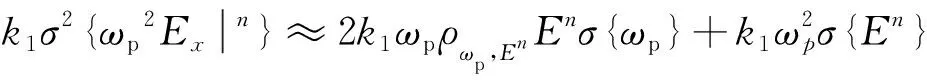
(15)

k2σ2ωp2Exn-1≈2k2ωpσωpExn-1+k2ωp2σExn-1

(16)

將式(15)～(16)代入式(14)中，可以得到等離子體中的S-PLRC-FDTD輔助變量標準差的迭代公式為：

(17)

需要指出的是，式(13)與式(17)中等離子體頻率與電場相關系數ρωp,Ex仍需要進一步確定，其取值會直接影響S-PLRC-FDTD對場量標準差的估計。

2 計算模型與結果分析

鞘套電子密度分布常采用雙指數或雙高斯模型描述。在本文計算中，假設鞘套內穩態(平均)電子密度分布具有如下雙高斯分布特性：

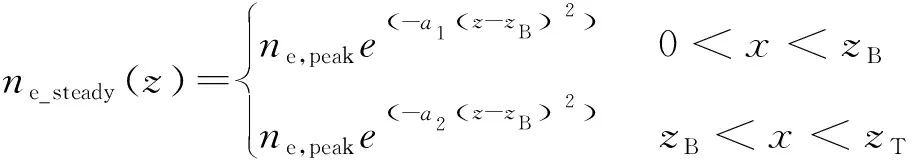
(18)

式中：ne,peak為電子密度峰值，zT為等離子體厚度，zB為峰值電子密度所處位置，a1,a2為描述電子密度衰減程度的參數。

由于電子密度分布受飛行高度，飛行速度，再入攻角，再入湍流等因素的影響，鞘套中電子密度并不恒定，電子密度具有一定的隨機特性，其電子密度可用如下模型描述：

ne(z)=ne_steadyz1+Δδne

(19)

式中：Δ表示電子密度相對變化幅度，δne為一標準正態分布隨機變量，因此電子密度標準差σne可以表示為σne=Δ·ne_steady，相應的等離子體角頻率方差可以表示為σωp=0.5Δωp_steady。

選取鞘套參數如下：a1=1 cm-2，a2=0.5 cm-2，zT=15cm,zB=5cm，峰值電子密度均值ne,peak=1×1017m-3，碰撞頻率υ=1×109rad/s。采用S-PLRC-FDTD方法，分別計算了電子密度相對變化幅度Δ=5%，Δ=10%，Δ=20%時，其對電波傳播的影響。S-PLRC-FDTD采用1 mm均勻網格剖分，時間步長Δt=Δz/2c。計算模型見圖 1，等離子體占據50～199網格(15 cm)。所加源為電場x方向極化的正弦平面波，其振幅為1 V/m，位于z方向第40網格處，觀測點位于第210網格處。

圖1 計算模型Fig.1 Simulation model

圖2給出了入射波頻率為1 575 MHz和4 000 MHz正弦波時，不同電子密度變化下，S-PLRC-FDTD方法計算得到的觀測點電場平均值。由于等離子鞘套的存在，透射電磁波存在衰減，透射波電場振幅分別衰減到0.544 V/m(衰減5.3dB)和0.941 V/m(衰減0.45 dB)。入射波頻率越高，衰減越小。

圖2 平面波入射時觀測點電場均值比較Fig.2 Comparison of mean electric field values in plane wave incident

為了驗證S-PLRC-FDTD方法的正確性，將Monte Carlo結合傳統PLRC-FDTD計算結果也繪于圖2中(Monte Carlo方法共采用1000組樣本)。可以發現S-PLRC-FDTD方法與Monte Carlo方法計算的電場平均值幾乎重合。

圖3分別給出1 575 MHz平面波入射下，電子密度相對變化幅度分別為Δ=5%，Δ=10%，Δ=20%時，觀測點電場在不同時刻的電場的方差值。與預期結果一致，當電子密度變化(標準差)越大，電場的方差也就越大。

在S-PLRC-FDTD方法中，Ex與ωp互相關系數ρEx,ωp的選取，會直接影響到電場方差的計算結果。ρEx,ωp=1時S-PLRC-FDTD會過高地估計電場的方差，相應的，當ρEx,ωp=0.8時，估計值偏低。在本例中，當ρEx,ωp=0.95時，S-PLRC-FDTD與Monte Carlo結果吻合最好。

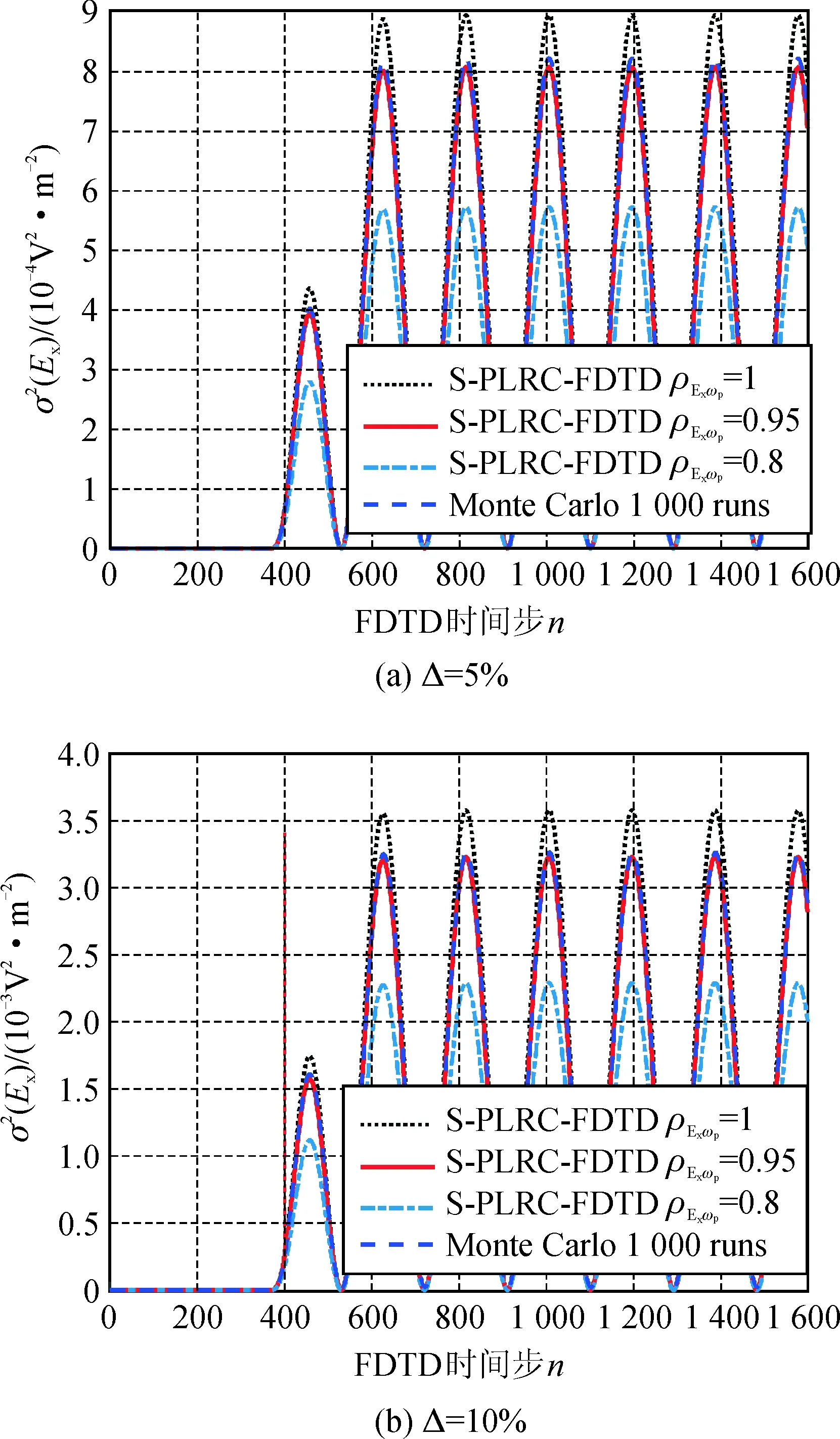
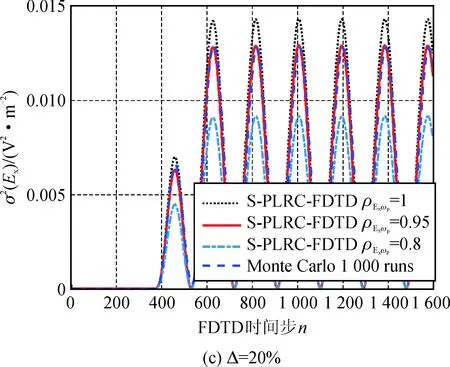
圖3 1 575 MHz平面波入射時觀測點方差比較電子密度相對變化幅度Fig.3 Comparison of observation point variances in 1 575 MHz plane wave incident

筆者也對4 000 MHz平面波入射情況進行了計算，同樣當ρEx,ωp=0.95時，S-PLRC-FDTD結果與Monte Carlo結果吻合最好。

由于S-PLRC-FDTD在每次迭代過程中，需要額外計算各場量的標準差，因此S-PLRC-FDTD內存占用及每步計算用時約為傳統PLRC-FDTD的2倍。但相比于傳統PLRC-FDTD需要通過1 000次甚至更多的Monte Carlo仿真獲得統計特性，S-PLRC-FDTD具有顯著優勢。

為進一步評估電子密度隨機變化對電磁波相位和幅度的影響，采用S-PLRC-FDTD方法，計算了上述鞘套在不同入射波頻率以及不同碰撞頻率情況下，透射系數幅度與相位的變化情況。

圖4給出了電子密度相對變化幅度Δ=10%時，透射系數幅度1σ誤差棒圖。從圖4中可以發現，當入射波頻率較低ω/ωp?1時，透射系數隨著碰撞頻率的增加而增加，當入射波頻率較高時，透射系數隨著碰撞頻率的增加而減少。

圖4 電子密度相對變化幅度Δ=10%時不同碰撞頻率下透射系數幅度的1σ誤差棒圖Fig.4 1σ error bar graph of transmission coefficientamplitude at different υ/ωp in the relative intensity of electron density variability Δ=10%

圖5給出了電子密度相對變化幅度分別為Δ=5%，Δ=10%，Δ=20%時，不同碰撞頻率下，透射系數幅度的標準差隨入射波頻率的變化。

從圖5可以發現，透射系數幅度標準差正比于電子密度相對變化幅度變化。從圖5中還可以發現，等離子碰撞頻率越高時，透射系數標準差隨入射波頻率變化越緩慢，當υ/ωp>1時，低頻段透射系數標準差基本不變；對高頻入射波ω/ωp>1，透射系數標準差隨著入射波頻率的增加而減小，并且碰撞頻率越小，透射系數標準差減小越快。總體而言，提高入射波頻率有利于減低電子密度變化對透射系數幅度的影響。

圖6給出了電子密度相對變化幅度分別為Δ=5%，Δ=10%，Δ=20%時，透射系數相位標準差隨入射波頻率的變化。

從圖6中可以發現，透射系數相位標準差同樣正比于電子密度相對變化幅度。在電子密度變化幅度相同時，碰撞頻率越高，透射系數相位標準差越小，隨入射波頻率的變化也越緩慢，并且對于低碰撞頻率υ/ωp≤1的等離子體，透射系數相位標準差最大值出現在ω/ωp≈1附近，隨著碰撞頻率的提高，透射系數相位標準差最大值逐漸向高頻方向移動。

圖5 不同碰撞頻率下透射系數標準差比較Fig.5 Comparison of standard deviations of transmission coefficient amplitude at different υ/ωp

表1和表2進一步給出了電子密度相對變化幅度Δ=10%時，S-PLRC-FDTD方法與Monte Carlo結合SMM方法(1 000次樣本)計算結果比較。

從表1～2中可以發現，S-PLRC-FDTD方法的計算結果與Monte Carlo結合SMM方法的計算結果具有很好的一致性。與Monte Carlo結合SMM方法相比，S-PLRC-FDTD方法的優勢在于它可以通過一次計算，獲得觀測點波形在所有時刻的均值與方差。

此外，對于更為復雜的鞘套模型(二維或三維情況)，S-PLRC-FDTD方法也具有適用性。

圖6 不同碰撞頻率下透射系數相位標準差比較Fig.6 Comparison of standard deviations of transmission coefficient phase at different υ/ωp

υ/ωpMonte Carlo + SMM方法下的標準差/(°)S-PLRC-FDTD方法下的標準差/(°)ω/ωp=0.2ω/ωp=0.5ω/ωp=1ω/ωp=2ω/ωp=0.2ω/ωp=0.5ω/ωp=1ω/ωp=20.10.877 03.165 04.004 92.037 50.848 33.142 93.913 32.064 80.50.088 41.048 42.426 61.873 10.072 50.958 22.436 21.846 510.048 70.380 51.263 71.523 50.035 80.388 41.238 71.515 550.006 00.023 30.084 00.228 90.004 50.024 00.081 90.224 2100.001 80.006 40.021 80.062 80.001 40.006 50.020 90.056 4

表2 透射系數幅度標準差

3 結 語

本文采用S-PLRC-FDTD方法，計算了電子密度為高斯分布的等離子鞘套中電子密度隨機變化對入射信號的影響，分析了電子密度抖動引入的相位抖動和振幅抖動。結果表明：電子密度的隨機變化與其引起透射電磁波的幅度與相位的抖動具有顯著的正相關性；在相同電子密度變化條件下，υ/ωp越大，透射系數幅度與相位的標準差隨頻率的變化越小；對于低碰撞頻率υ/ωp≤1的等離子體，透射系數相位標準差最大值出現在ω/ωp≈1附近，隨著碰撞頻率的提高，透射系數相位標準差最大值逐漸向高頻方向移動；總體而言，提高入射波頻率，有助于有減少透射電磁波幅度與相位抖動。