長時間小過載情況下固體火箭發動機兩相流流場數值模擬①

那旭東，夏智勛，馬立坤，顏小婷

(國防科技大學 空天科學學院，長沙 410073)

0 引言

近年來，隨著反導攔截能力需求的不斷提升，對高機動性能導彈發動機在過載情況下的可靠性和安全性均提出了更高要求。該類導彈的動力系統基本上采用高機動性能的固體火箭發動機，如美國的PAC-3、俄羅斯S-300V等，其主要技術特點是導彈在高機動運動過程中，要承受長時間小過載、中時間中過載、短時間大過載等過載情況[1-2]。高機動性能的固體火箭發動機大多采用含鋁復合固體推進劑[3-4]，其燃燒產物中含有大量凝相顆粒Al2O3，發動機內流場是典型的氣固兩相流場。在過載條件下，高速凝相顆粒運動會引起燃燒室和噴管的局部聚集和沖刷，使局部燒蝕加劇，對發動機熱防護結構產生很大影響。嚴重時會造成內絕熱防護失效、殼體燒穿，從而導致飛行失敗[5]。因此，研究和掌握過載條件下發動機內流場顆粒流的運動規律，對提升高機動性能固體火箭發動機的安全性及可靠性都具有重要的實現意義。

關于過載情況下固體火箭發動機內流場的兩相流流動，國內外都進行了相關研究[6-18]，但對長時間小過載情況下發動機燃燒室及噴管的三維二相流流動的研究報道則較少[19-20]。本文以某飛行試驗失敗發動機為研究對象，針對其長時間小過載的工作特點，對燃燒室及潛入式噴管進行三維兩相流流場的數值計算，在計算過程中，考慮了發動機旋轉所帶來的科氏加速度的影響。通過仿真計算分析了發動機內部兩相流流場，并給出顆粒沉積區域及對應的顆粒沖刷角度、沖刷速度、顆粒粒徑及濃度分布，旨在研究在長時間小過載條件下發動機內部顆粒的流動及沉積情況，為該類發動機后續的熱防護設計提供指導依據。

1 計算模型和方法

1.1 發動機構型及網格劃分

以某飛行試驗固體火箭發動機為研究對象，該發動機采用翼柱形裝藥。對該發動機工作過程中3個典型時刻t1、t2和t3進行定常計算。其中，t1時刻為法向過載最大時刻；t2時刻為法向過載變小的拐點；t3時刻為裝藥完全燒完時刻。t1～t3典型時刻發動機幾何構形如圖1所示，主要包括前后封頭、藥柱、發動機殼體以及潛入式噴管。

采用六面體結構網格對發動機進行網格劃分，并對壁面處及預估顆粒沉積量大的地方進行網格加密。圖2給出了t1時刻其網格劃分結果，其中上面為采用結構網格劃分的塊拓撲結構，下面為對應的發動機三維結構網格。

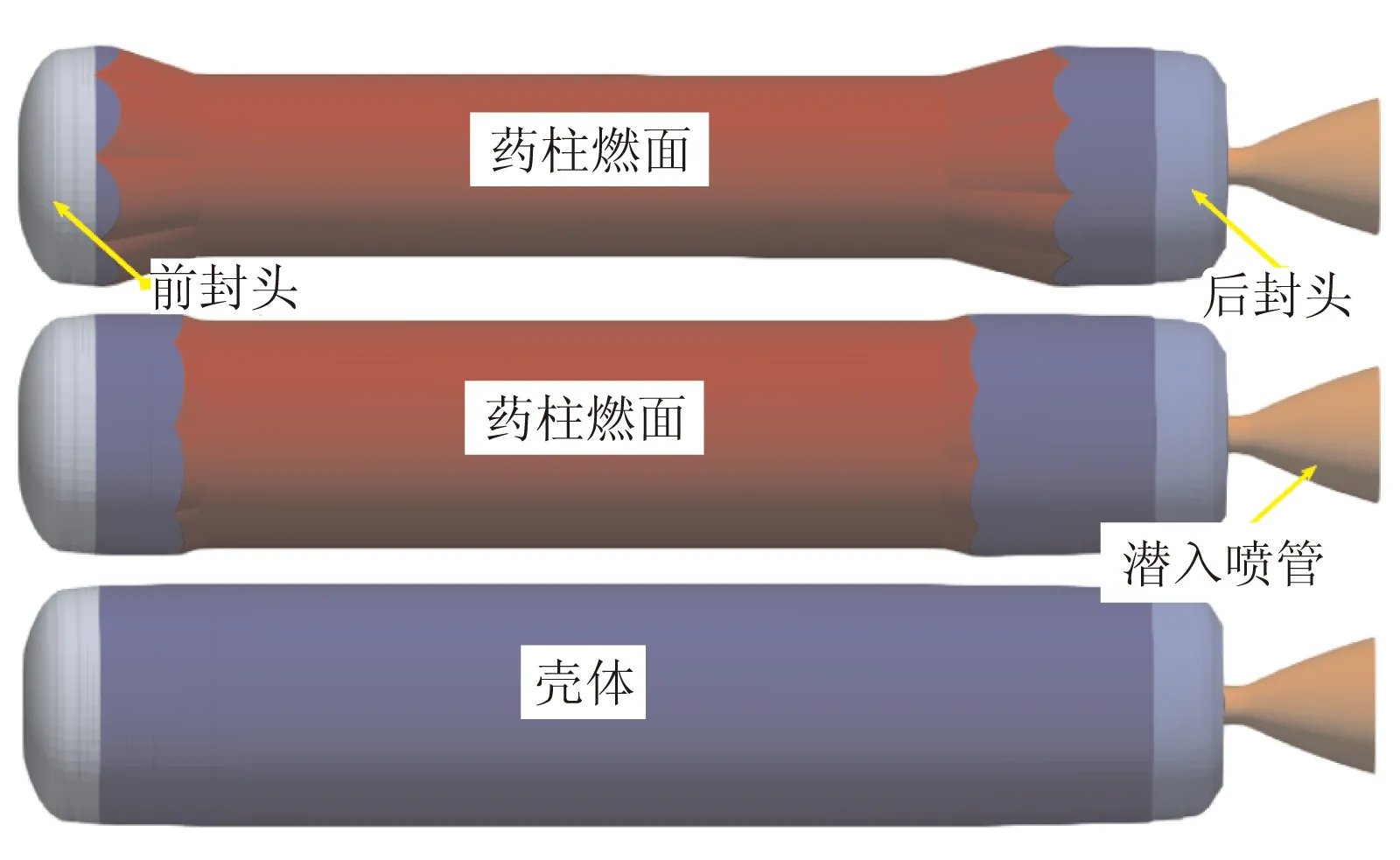
圖1 發動機幾何模型

1.2 數值方法及相關參數

采用Fluent軟件開展仿真計算，兩相流流動使用離散相模型DPM(Discrete Phase Model)求解。燃氣作為連續相在歐拉坐標系下求解，顆粒相作為離散相進行處理，對每個顆粒在拉格朗日坐標下進行跟蹤。燃氣的控制方程采用N-S方程，顆粒相的運動軌跡則由拉格朗日方程確定[17]。

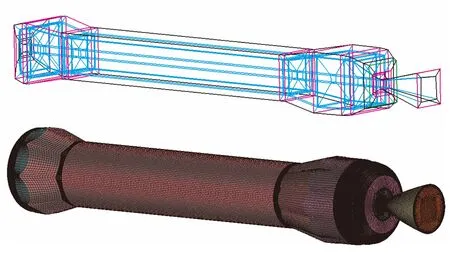
圖2 t1時刻發動機塊拓撲結構及網格劃分

鑒于本文主要研究發動機中氣相及顆粒相在長時間小過載條件下的流動特性，針對過載條件下發動機流動的特點，將復雜的兩相流流動模型進行適當簡化[21]：

(1)不考慮燃面退移過程，對選定的時刻進行定常計算；

(2)不考慮化學反應，將發動機內復雜的多組分氣體簡化為單一燃氣，典型時刻的相關燃氣參數見表1；

表1 發動機燃氣參數

(3)燃氣控制方程采用三維可壓粘性N-S方程，采用標準k-ε湍流模型；

(4)固相顆粒為球形Al2O3，不考慮顆粒相的燃燒、蒸發、破碎過程以及顆粒間撞作用，忽略顆粒相變及密度變化的影響；

(5)忽略過載對氣相的影響，對固相的作用通過UDF施加體積力給出。

顆粒直徑分布采用Rosin-Rammler分布[18]，即假定顆粒直徑d與大于直徑的顆粒質量分數Yd之間有如下指數關系：

(1)

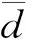
結合發動機所采用推進劑配方和文獻[20, 22-23]，選取粒度分布范圍為10～100 μm，顆粒直徑分布指數為3.5，粒徑平均直徑為55 μm，顆粒的直徑分布曲線如圖3所示。

由于燃燒溫度(見表1)明顯高于Al2O3熔點溫度2318 K ，所以固相顆粒的參數按液相Al2O3物性參數給定[24-27]，其中密度為2700 kg/m3、比定壓熱容1883 J/(kg·K)、熱導率7.4 W/(m·K)。

顆粒壁面碰撞模型對模擬固體火箭發動機殼體內顆粒的沉積分布至關重要。Mundo等[28-29]基于大量實驗認為，液滴撞擊到壁面后的狀態主要由液滴的動能決定，并提出了以Sommerfeld數K=We0.5·Re0.25的大小為判定準則，當K≤57.7時，液滴粘附于絕熱材料壁面；反之，液滴在絕熱材料表面發生反彈飛濺，其中We與Re分別為入射液滴的韋伯數與雷諾數[30-31]。

本文采用以Sommerfeld數為判定準則的顆粒壁面碰撞模型，對固體火箭發動機內顆粒碰撞壁面后狀態進行判定。

1.3 邊界條件處理

計算過程中主要用到三類邊界條件：加質面邊界條件、固壁面邊界條件及出口邊界條件。

(1)加質面邊界：根據發動機實際設計情況給出當前時刻推進劑表面的質量流量，其中凝相占總質量流量的30%。顆粒從加質壁面均勻加入，在推進劑表面上應用反彈模型，在前封頭、后封頭及噴管固壁面上通過Sommerfeld數判定顆粒在壁面處的行為，在噴管出口應用消匿模型。

(2)固壁面邊界條件：采用無滑移條件，即認為壁面處流體速度與該處壁面速度相同，法向壓力、溫度梯度為0。

(3)出口邊界條件：發動機噴管出口氣流處于超聲速狀態，給定出口處背壓。

1.4 計算策略及驗證方法

計算過程中，為節約計算時間，首先進行燃氣流場穩態計算，燃氣流場穩定后再添加顆粒項進行兩相流場計算。連續相每計算200次進行一次顆粒的計算，顆粒計算的迭代步數為2000步。計算結果與表1中噴管喉部及噴管出口的壓強、溫度、馬赫數等參量進行對比，驗證數值結果的可靠性，并對網格無關性進行驗證。

2 彈體坐標系及顆粒受力分析

2.1 彈體坐標系

彈體坐標系見圖4。

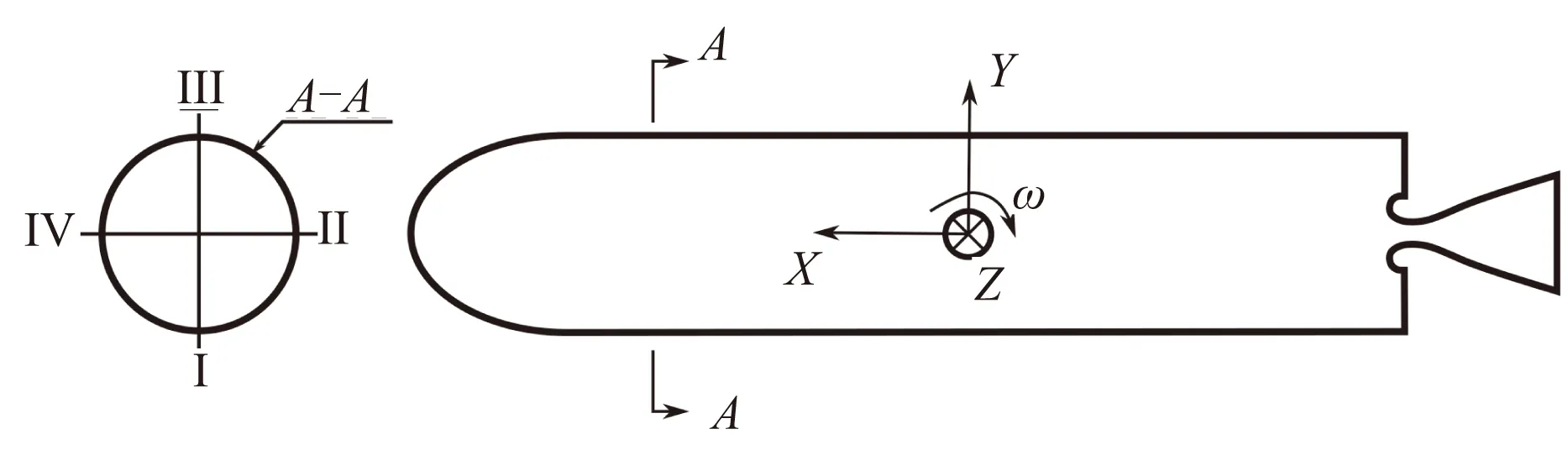
圖4 彈體坐標系

圖4 中，坐標系遵循右手定則，X軸為彈體軸向方向，指向彈頭方向為正向，Y、Z軸垂直于X軸，Y軸位于Ⅲ軸上，Z軸位于Ⅳ軸上。軸向過載方向為X軸方向，法向過載方向為Y軸方向，橫向過載方向為Z軸方向。

2.2 顆粒受力分析

在導彈飛行過程中，存在繞Z軸的角速度ω。當牽連運動為轉動時，動點在某瞬時的絕對加速度等于該瞬時它的相對加速度、牽連加速度與科氏加速度的矢量和[32]。因此，發動機中的固體顆粒除了存在橫向、軸向及法向的過載加速度外，還應考慮顆粒所受的科氏加速度。

顆粒的絕對加速度為

a絕=a相+a牽+a科

式中a絕為質點在慣性系中的加速度。

牽連加速度為

a牽=α×r+ω×(ω×r)

式中α為角加速度；r為顆粒位置矢量。

科氏加速度為

a科=2ω×v′

式中v′為顆粒相對于動坐標系的相對速度。

假定發動機3個方向的過載加速度分別為a軸、a法和a橫，發動機繞Z軸的角速度為ω，忽略角加速度α，則有：

相對加速度為

a相=-(a軸+a法+a橫)

牽相加速度為

a牽=ω×(ω×r)

科氏加速度為

a科=2ω×v′

將慣性坐標系設定在發動機上，在慣性坐標系中研究發動機中固相顆粒加速度，則固相顆粒所受的加速度為

a=a相+a牽+a科

=-a軸-a法-a橫+

ω×(ω×r)+2ω×v′

可得絕對加速度在慣性直角坐標系下的3個分量分別為

ax= -a軸+[ωj(ωirj-ωjri)-ωk(ωirk-ωkri)]i+

ay= -a法+[ωi(ωirj-ωjri)-ωk(ωjrk-ωkrj)]j+

az= -a橫+[ωi(ωirk-ωkri)-ωj(ωjrk-ωkrj)]k+

由于導彈只存在Z軸方向上的角速度，因此ωi=0，ωj=0，所以絕對加速度在發動機慣性直角坐標系下的3個分量最終表達式為

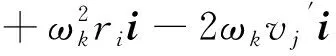
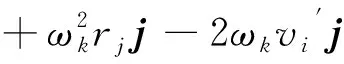
az=-a橫

通過UDF的宏DEFINE_DPM_BODY_FORCE在計算中對顆粒施加過載加速度。所有變量單位采用國際單位制，角速度的單位為rad/s，加速度的單位為m/s2，速度的單位為m/s，顆粒位置矢量單位為m。t1～t3典型時刻的過載數值見表2。

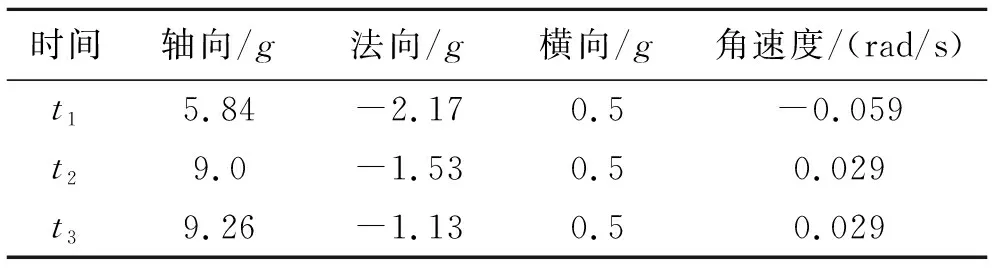
表2 過載數值

3 計算結果分析

對該發動機在3個典型時刻下分別進行定常計算。圖5分別為t1～t3時刻，Z=0平面處發動機內流場的馬赫數、速度、壓強及溫度場計算結果。將圖5中的數據與表1中噴管喉部及噴管出口的馬赫數、壓強和溫度的數值對比，其結果基本一致。圖5中，噴管二相流流場的速度和溫度分布受顆粒的影響較大，而壓力場受顆粒的影響較小。從速度場可看出，噴管軸心處的速度要小于接近壁面處的速度，而軸心處的溫度要高于接近壁面處的溫度，這是由于顆粒的滯后性造成的，是典型的氣固顆粒流流場特征[33]。

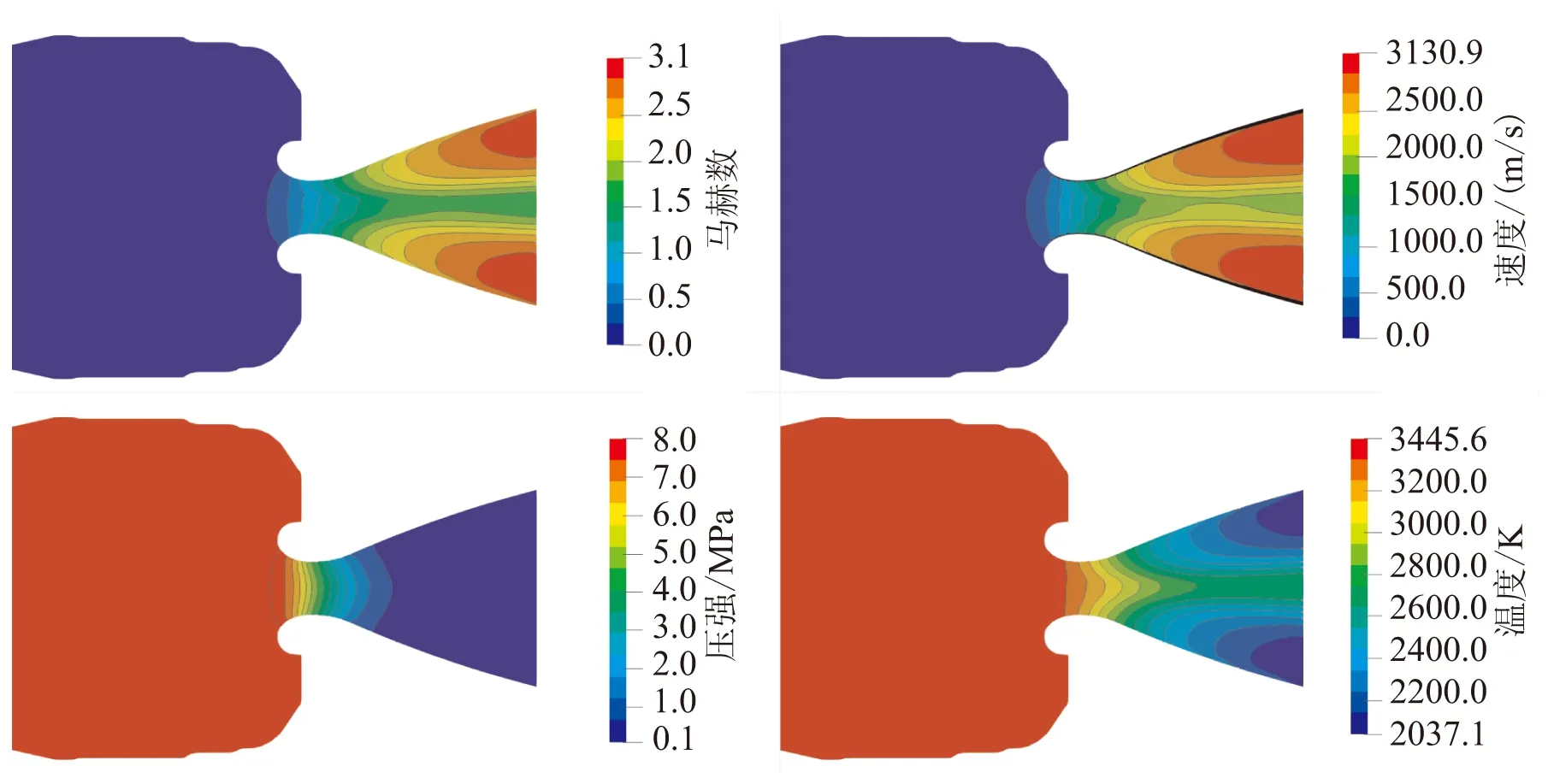
(a)t1時刻

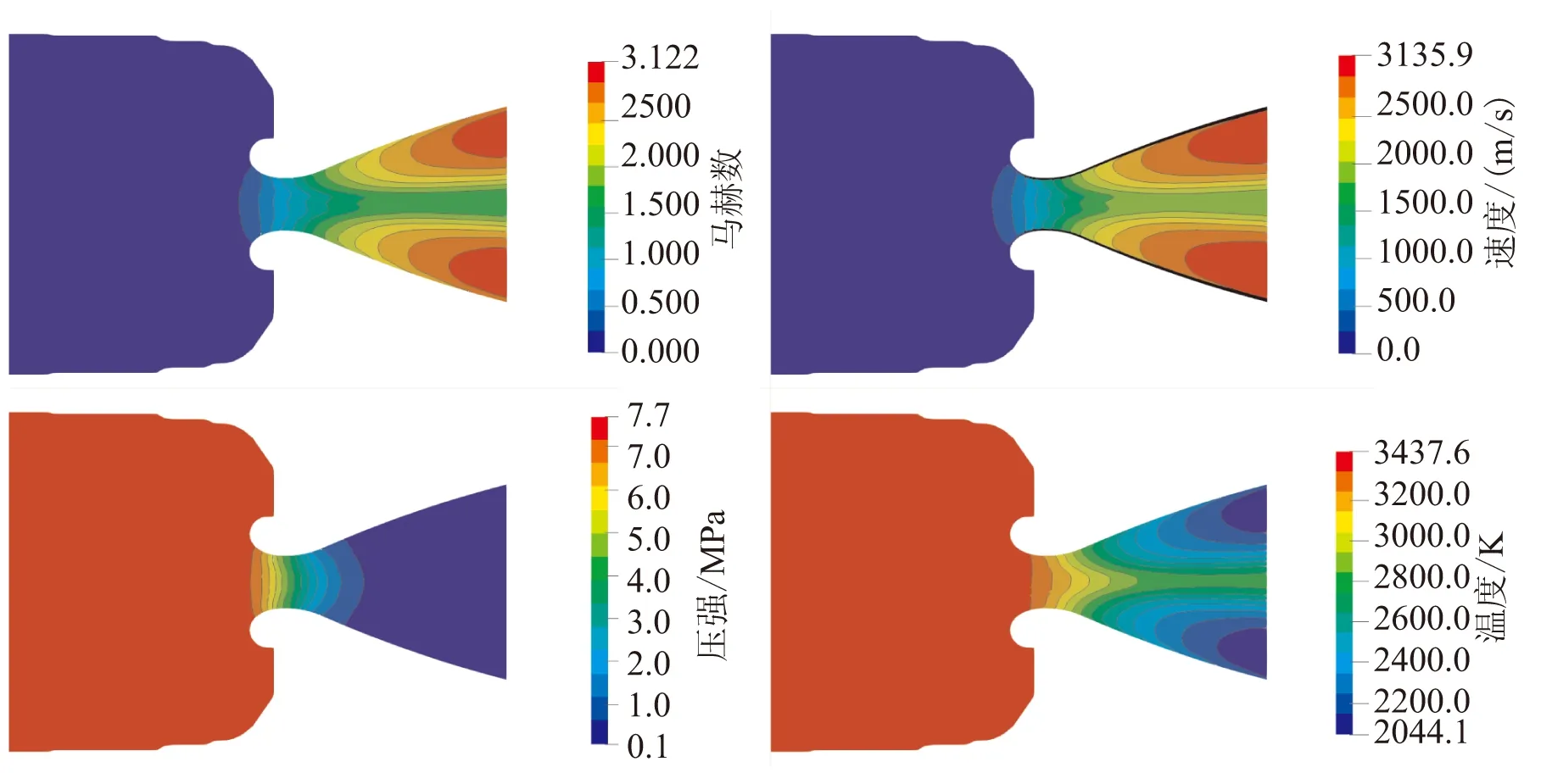
(b)t2時刻

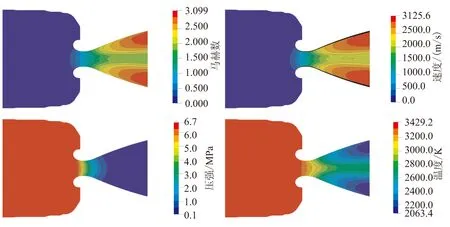
(c)t3時刻

圖6給出了3個典型時刻的顆粒軌跡線分布情況。從圖6可看出，顆粒從推進劑表面進入燃燒室后，在燃氣氣流的帶動下迅速向發動機軸線方向靠近，與發動機壁面幾乎不發生碰撞，而在離后封頭及噴管較近的某些位置進入流場的顆粒比較容易撞擊壁面，從而形成沉積。此外，從噴管處顆粒的軌跡可看出，大尺寸的顆粒基本沿噴管軸線附近區域流動，而小尺寸的顆粒遠離噴管軸線區域流動。這主要是小尺寸顆粒的隨流性較好，在氣流帶動作用下軌跡發生了偏轉。

圖7給出了t1時刻發動機顆粒沉積濃度分布情況。可看出，濃度分布較大的位置主要集中在后封頭圓弧過渡段及潛入式噴管潛入段壁面處。

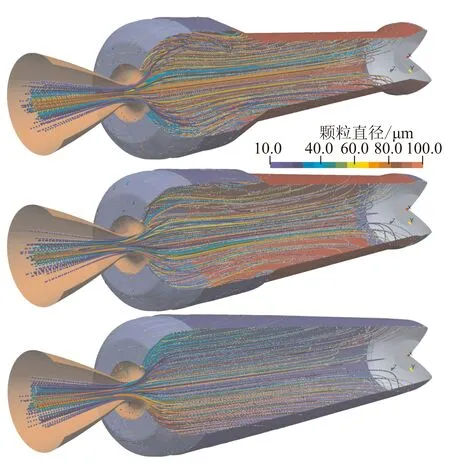
圖6 顆粒軌跡線

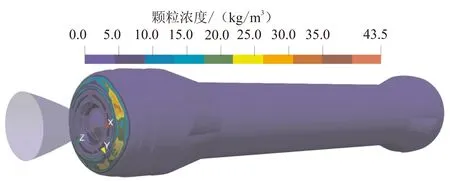
圖7 t1時刻顆粒沉積濃度分布

圖8為t1、t2和t3時刻發動機后封頭及噴管處顆粒沉積濃度分布放大圖。其中，左圖為從發動機外部視角觀測顆粒沉積濃度分布；右圖為從發動機內部視角觀測后封頭及潛入式噴管濃度分布。

從圖8(a)可看出，后封頭處的顆粒沉積濃度要大于噴管處，主要集中于后封頭圓弧過渡段處，且在承載方向上沉積濃度發生偏轉。從圖8(b)可看出，t2時刻其后封頭圓弧過渡段處顆粒沉積濃度分布沒有發生明顯的偏轉，但其仍為顆粒沉積濃度分布最大處，在噴管潛入段及與其相鄰的后封頭平面處顆粒沉積濃度在承載方向上發生了偏轉。從圖8(c)可看出，t3時刻其顆粒沉積濃度在后封頭圓弧過渡段處和噴管潛入段處在承載方向上發生了偏轉，且顆粒沉積濃度最大處仍處于圓弧過渡段處。

針對t1時刻的工況，除了考慮所有過載情況下的計算，還進行了無過載計算及無橫向過載計算。圖9與圖10分別為無過載及無橫向過載條件下后封頭及噴管處顆粒沉積濃度分布。分析對比圖8(a)、圖9和圖10可知，對于后封頭圓弧過渡段，當無過載時顆粒的沉積在周向方向上分布相對均勻，無明顯聚集偏轉，最大沉積量約為23 kg/m3；當有過載時沉積的分布發生了明顯的偏轉，在承載方向上沉積量有所增加，考慮所有過載情況下時的最大沉積量約為42.5 kg/m3，約為無過載情況下的1.89倍；無橫向過載(0.5g)情況下的最大沉積量約為42.8 kg/m3，兩者之間差距并不明顯。

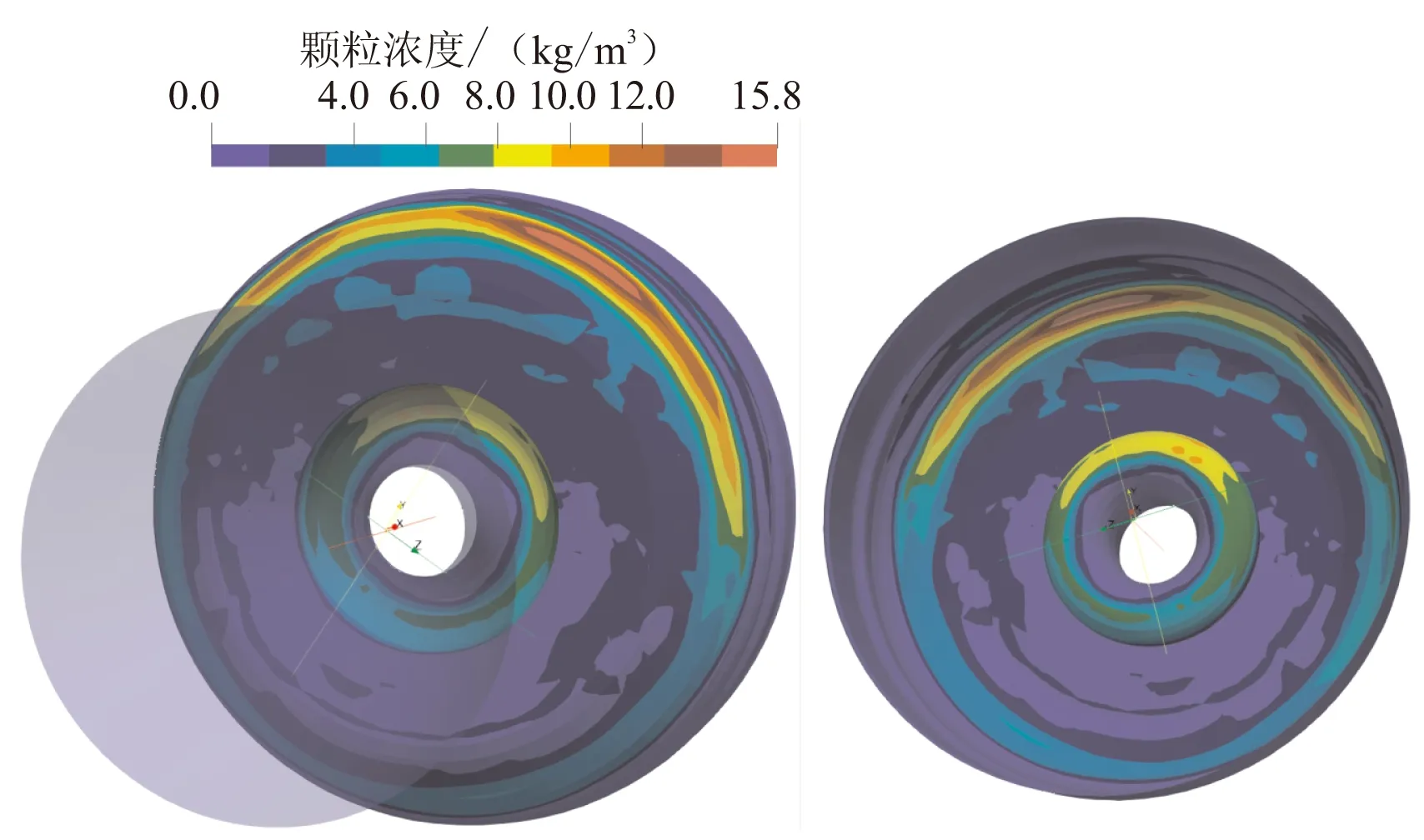
(c) t3時刻

由于顆粒的沖刷速度與沖刷角度對研究顆粒對絕熱層的沖擊燒蝕具有重要意義，因此對圖8(b)、(c)及圖9中后封頭圓弧過渡段處顆粒的沖刷速度及角度進行統計，結果見圖11和圖12。從圖12可看出，顆粒在后封頭圓弧過渡段處的入射角度大多在20°～40°之間，屬于切向的剪切沖蝕。

此外，還對后封頭圓弧過渡段處顆粒尺寸進行了統計，如圖13所示。可看出，后封頭圓弧過渡段處沉積的顆粒主要為相對較大尺寸的顆粒。

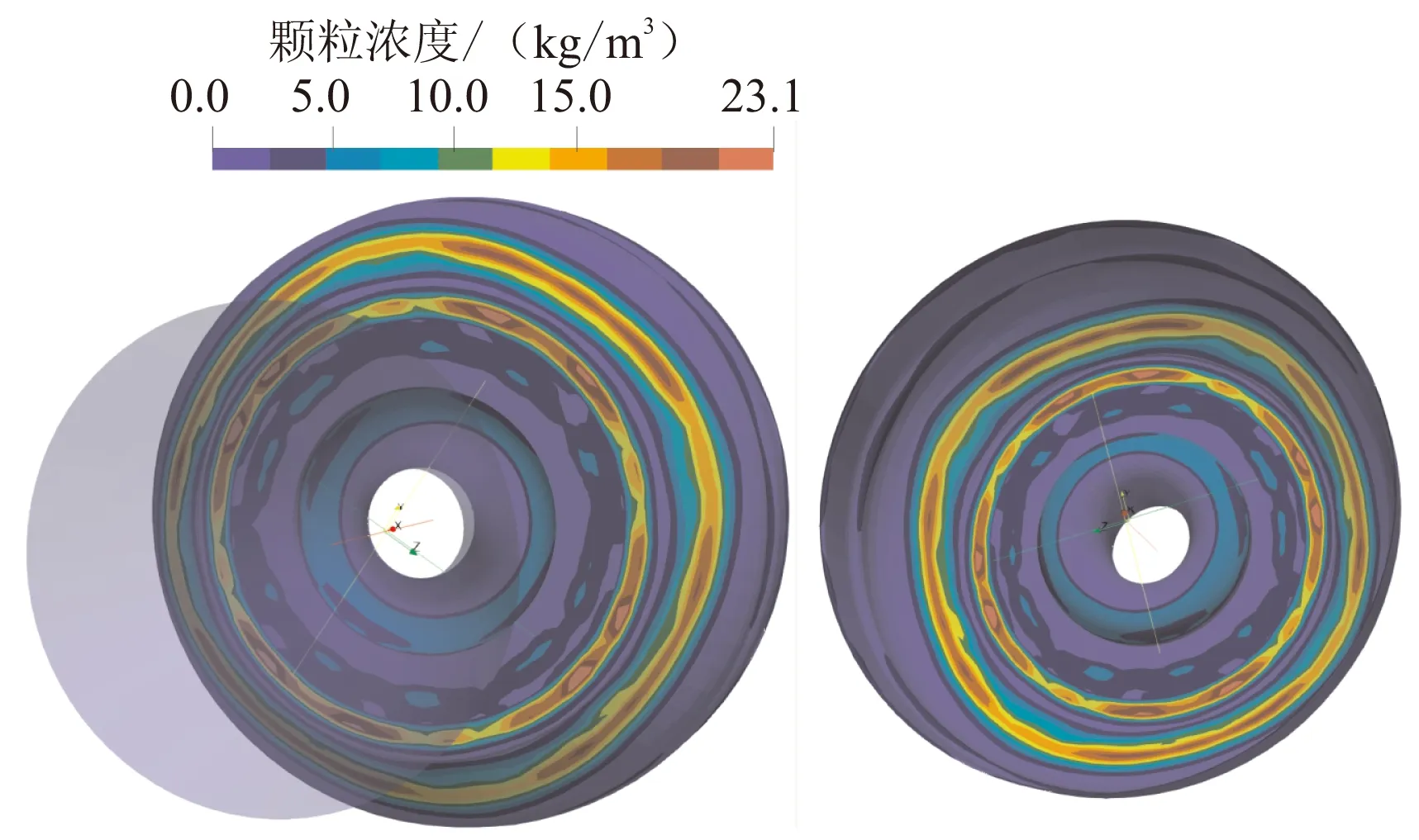
圖9 t1時刻無過載條件下后封頭及噴管顆粒沉積濃度分布

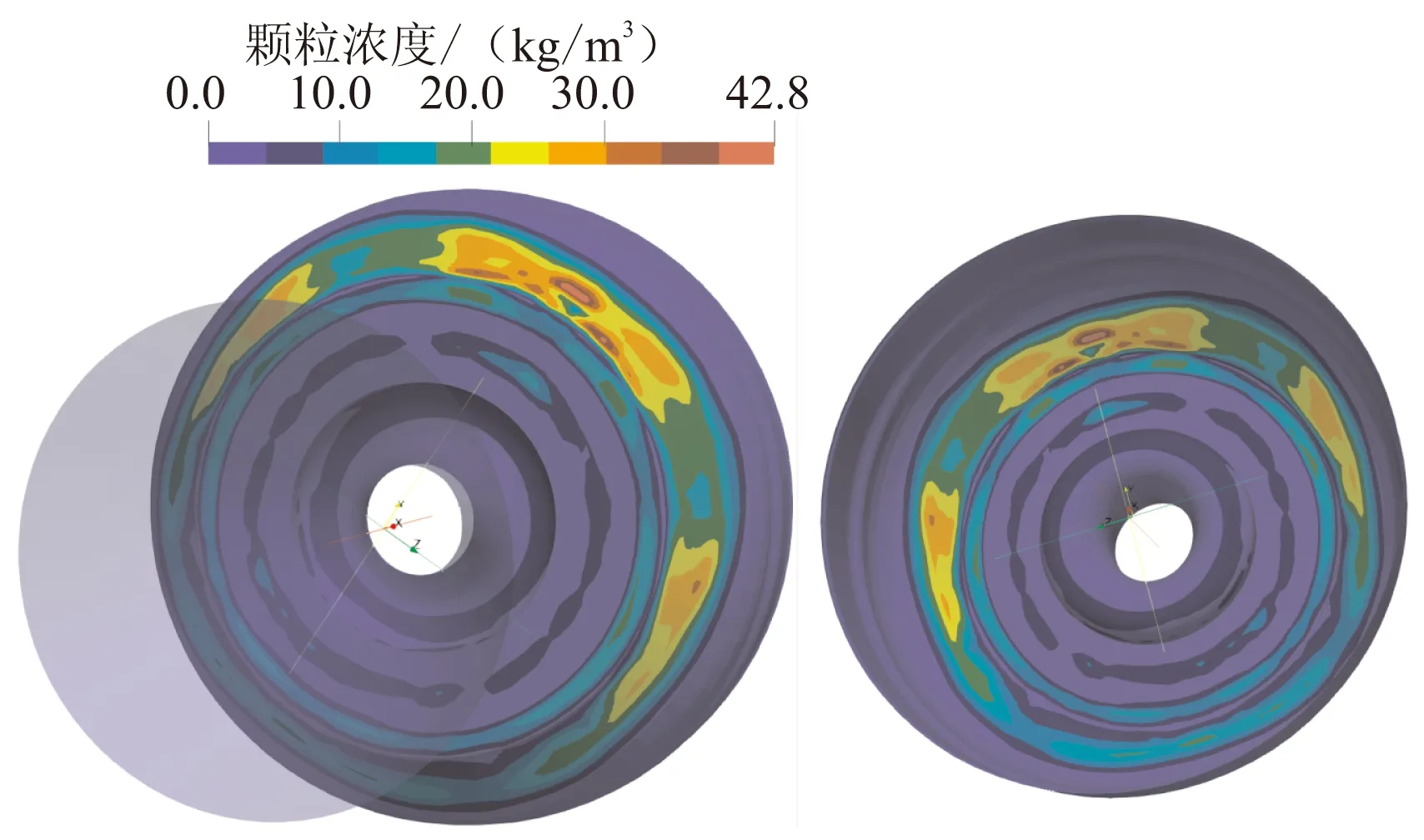
圖10 t1時刻無橫向過載條件下后封頭及噴管顆粒沉積濃度分布

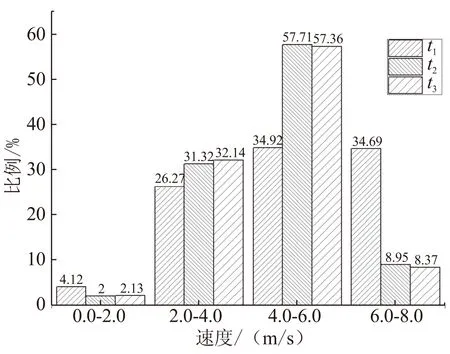
圖11 后封頭圓弧過渡段處顆粒的沖刷速度分布

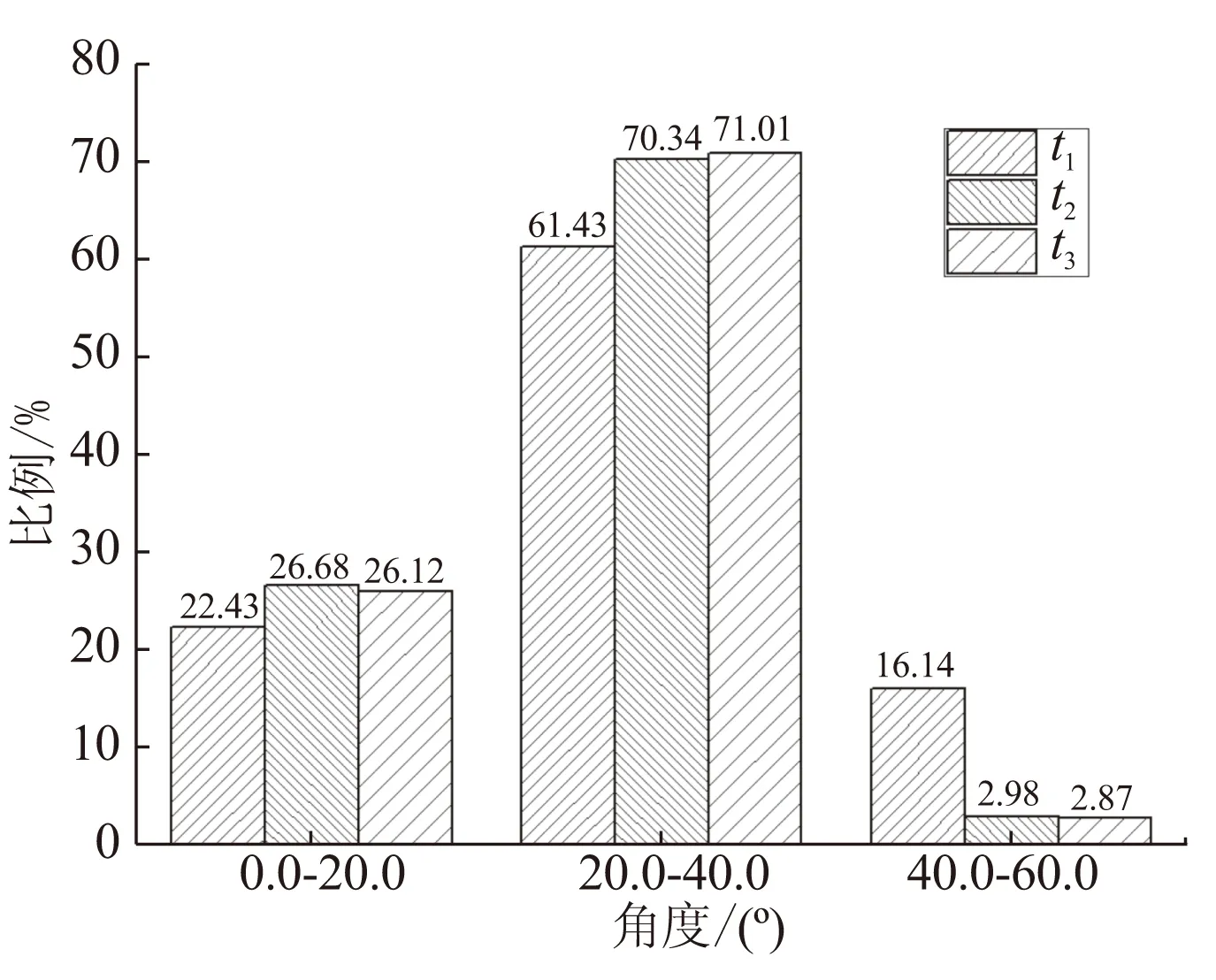
圖12 后封頭圓弧過渡段處顆粒的沖刷角度分布

圖13 后封頭圓弧過渡段處顆粒的粒徑分布

從以上仿真結果可知，在進行此類發動機絕熱層設計時，要充分考慮發動機在長時間小過載情況下所帶來的影響，對顆粒沉積量大的地方，要加大絕熱層的厚度，以防將發動機殼體燒穿，造成發動機失效。

4 結論

(1)本文以某飛行失效固體火箭發動機為研究對象，針對其長時間小過載的工作特點對其三維兩相流內流場進行數值模擬，在計算過程中考慮了發動機旋轉所帶來的科氏加速度的影響。分析了兩相流流場特性，并給出了凝相顆粒沉積位置、沉積量及顆粒的沖刷速度、角度和粒徑的統計分布。

(2)分析3個典型時刻下的顆粒沉積分布，指出沉積量大的位置主要集中在后封頭圓弧過渡段處，且沉積的分布發生了的偏轉，在承載方向上沉積量有所增加。針對t1時刻，分析對比無過載、無橫向過載以及考慮所有過載的情況，相比無過載情況，考慮所有過載時，其最大沉積量為無過載情況下的1.89倍。

(3)在此類發動機后續設計過程中，要充分考慮長時間小過載情況下兩相流流場對發動機帶來的影響，在顆粒沉積量大的地方要進行充分的熱防護。