基于程序頻譜的缺陷定位方法①

蔡 蕊， 張 仕，2， 余曉菲， 蔣建民，2

1(福建師范大學 數學與信息學院， 福建 350117)

2(福建師范大學 數字福建環境監測物聯網實驗室， 福建 350117)

隨著軟件項目的規模不斷變大， 軟件的可靠性也越來越難以保障. 精準、有效的軟件缺陷定位技術則有利于發現軟件中潛在的問題， 從而提高軟件的可靠性. 為修改測試中發現的問題， 需要進行程序的調試，其過程又可以分為缺陷定位和缺陷改正兩個步驟[1]. 早期的缺陷定位以人工為主， 通過在程序中設置斷點分析程序， 從而逐步找到缺陷發生的源頭. 人工定位缺陷的方法不僅難度大， 而且非常耗時， 對于大型、復雜的軟件則更是如此. 因此， 研究人員提出多種缺陷定位方法， 根據是否需要執行測試用例， 又可分為靜態缺陷定位技術[2-4]和動態缺陷定位方法[5-7]. 其中， 動態缺陷定位方法則需要執行被測程序， 搜集程序執行過程的行為和執行結果來定位缺陷. 在動態缺陷定位方法中， 基于程序頻譜的動態缺陷定位(SFL)具有很好的定位效果， 是目前軟件缺陷定位問題的研究熱點.

目前， 已經提出很多基于頻譜的缺陷定位方法[8]:其中， Jone等人首先提出Tarantula[9]方法， 取得不錯的缺陷定位效果； Abreu等人提出Jaccard[10]方法和Ochiai[11]方法， 其中Ochiai方法效果相比Tarantula方法有了一定的提高； Gonzalez增加了排除正確語句的優化， 提出了Zoltar方法[12]； Naish等人使用自組裝映射中計算相似度計算相似度的方法來尋找缺陷語句，引入Kulczynski1方法和Kulczynski2方法[13]； Wong 等人[14]進一步分析了成功測試用例數對缺陷定位的影響.他們認為， 語句被成功測試用例覆蓋的次數越多， 該語句的覆蓋次數對可疑值的貢獻度越小[15]， 因此提出了Wong1(s)、Wong2(s)和Wong3(s)三個公式， 但當成功執行的用例數量較多時， 利用分段函數降低成功用例的影響這些是不夠的， 將對缺陷定位效果的提高不會很明顯. 隨后為了突出失敗用例的影響， 又提出D*方法[16]. 通過實證研究發現D*方法要優于其他缺陷定位方法.

針對Wong1(s)、Wong2(s)和Wong3(s)分段函數不能自主適應用例數量這一缺點， 本文從成功執行用例數量調節出發， 提出EP*缺陷定位方法， 該方法具備自主調節成功測試用例覆蓋比重的能力， 以提高方法的適用性范圍和有效性. 本文把該方法與其他缺陷定位方法進行對比， 實驗結果表明該方法的缺陷定位效果優于現有缺陷定位方法.

本文的第1節介紹了基于頻譜的缺陷定位方法的基本概念， 并通過一個簡單的引例說明了本文方法的基本原理和公式； 第2節中詳細說明了本文實驗所使用的測試程序集及評測指標； 第3節中則通過對比分析， 詳細說明了EP*的有效性； 最后1節總結全文.

1 基于頻譜的缺陷定位方法

1.1 基本概念

Reps 等人[17]首次提出程序譜概念， 后面的研究者們將程序頻譜[18-20]用于程序分析. 程序頻譜主要是指程序執行過程中產生的關于程序語句的覆蓋信息(被覆蓋為1， 未覆蓋為0)， 以及執行是否通過信息.

在利用測試用例集進行程序的測試過程中， 收集程序語句的覆蓋情況和測試通過與否等相關信息， 將每一程序實體s相關的統計數據用一個四元組T(s)=＜Tep(s)，Tef(s)，Tnp(s)，Tnf(s)＞來表示， 其中Tep(s)和Tef(s)分別表示覆蓋程序實體s的成功測試用例數和失敗測試用例數，Tnp(s)和Tnf(s)分別表示未覆蓋程序實體s的成功測試用例數和失敗測試用例數. 測試套件T中所有成功測試用例數Tp=Tep(s)+Tnp(s)， 所有失敗測試用例數Tf=Tef(s)+Tnf(s)， 所有測試用例數T=Tp+Tf.

Tep(s)的數值越大， 說明語句s執行且用例成功的次數多，s是缺陷語句的可能性越小；Tef(s)的數值越大，說明語句s執行且用例錯誤的次數多，s是缺陷語句的可能性越大；Tnf(s)的數值越大， 則說明語句s沒有被執行到的情況下錯誤越多， 這間接說明s是缺陷語句的可能性越小.

1.2 EP*的缺陷定位方法

Wong等人[14]總結的假設5-7說明了:可疑值與Tef(s)大小成正比， 與Tep(s)大小和Tnf(s)大小成反比，可以設Kulczynski系數為1來表示Tef/(Tnf+Tep). 基于假設8對Tef設置更高的權重， 可以設置Kulczynski系數為2來表示2*Tef/(Tnf+Tep). 但Kulczynski系數在缺陷定位的準確性上不夠. 考慮到這一點， Wong等人提出采用*系數， 取值范圍從2～50增量為0.5. 提出D*方法， 通過實驗驗證該方法在缺陷定位上效果很好.

此外， 在文獻[21]中， 其通過預處理的方式去除部分測試用例， 也是希望減少成功執行數量對可疑值的過度影響， 以提高定位精度. 由預處理目的[21]和Wong等人D*公式啟發， 為了有效降低Tep(s)對整體數值的影響， 本文提出EP*方法， 如公式 (1)所示. 公式采用*系數， 取值范圍與D*一樣. 在具體的應用中，Tef數量要比Tep小很多， 在降低Tep的權重時對缺陷定位的影響會更加明顯.本文實驗也驗證了這個猜想， 說明了EP*方法的缺陷定位要比D*方法更優.

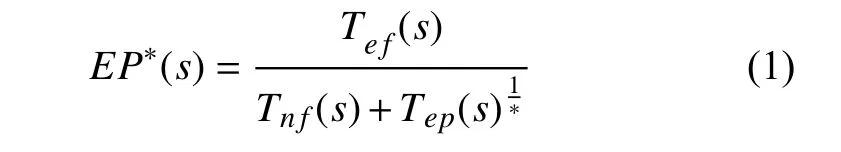
1.3 引例

為了更好的理解， 我們通過一個實例[16]來說明EP*缺陷定位方法. 在表1中， S表示待測程序的語句集， S={s1，s2，s3，s4，s5，s6，s7，s8，s9}， si表示具體的程序語句；P表示被測程序實體， 其中缺陷語句是s3；ti表示第i個測試用例執行對程序的覆蓋向量， 其中黑點代表該語句被執行， 反之未執行； 表1中最后一行的P/F表示執行成功與否， 0表示測試用例執行成功， 反之失敗；susp1表示測試用例基于Ochiai技術計算的可疑值；rank1表示程序中可疑值大于等于該語句的數量(含該語句本身). 從表1中可以看出， 缺陷語句s3的排名與語句s4并列第3， 表示為確保測試人員找到缺陷語句，最多需要檢查3條程序語句.

表1 示例程序表

表2對比了D*方法和EP*方法中的Kulczynski系數取為1、2、3時的示例程序排名情況. 結合表1， 可以發現， 當Kulczynski系數取 1時， 缺陷語句排名rank2=4；Ochiai方法的缺陷語句排名rank1=3， 則Kulczynski1方法的定位效果不如Ochiai方法. 當Kulczynski系數取2時，D*方法的缺陷語句排名rank3=3；EP*方法的缺陷語句排名rank5=2， 提升兩名，則EP*方法的定位效果比D*方法和Ochiai方法好. 當Kulczynski系數取3時，D*方法的缺陷語句排名rank4=2， 提升一名；EP*方法的缺陷語句排名rank6=2保持不變. 從該例中可以看出，EP*方法在取相同系數時， 能夠更快逼近最優值. 同時也可以發現， 由于s3和s4具有相同的覆蓋情況， 任何可疑度計算都無法區分二者， 即當Kulczynski系數取2和3時，rank5=2、rank6=2已經達到最佳缺陷定位效果.

在表2中， 語句s1、s3和s6的執行通過語句數分別是Tep=8、Tep=7和Tep=2.在Kulczynski1方法中不同的語句的覆蓋次數對懷疑率的貢獻度是一樣的， 但語句s1和s3的Tep值要比s6大很多， 所以s1和s3的排名都在s6后面， 而s1和s3的排名很接近. 在EP2方法中， 不同的語句的覆蓋次數對懷疑率的貢獻度不同， 其中Tep值越大， 貢獻度越低. 這樣就減弱了執行通過語句數Tep對語句s1、s3與s6的影響. 但s3中的Tef比s1和s6大， 所以s3的排名都在s1和s6前面. 因此EP*方法能夠減弱執行通過語句數Tep對可疑值的過度影響.

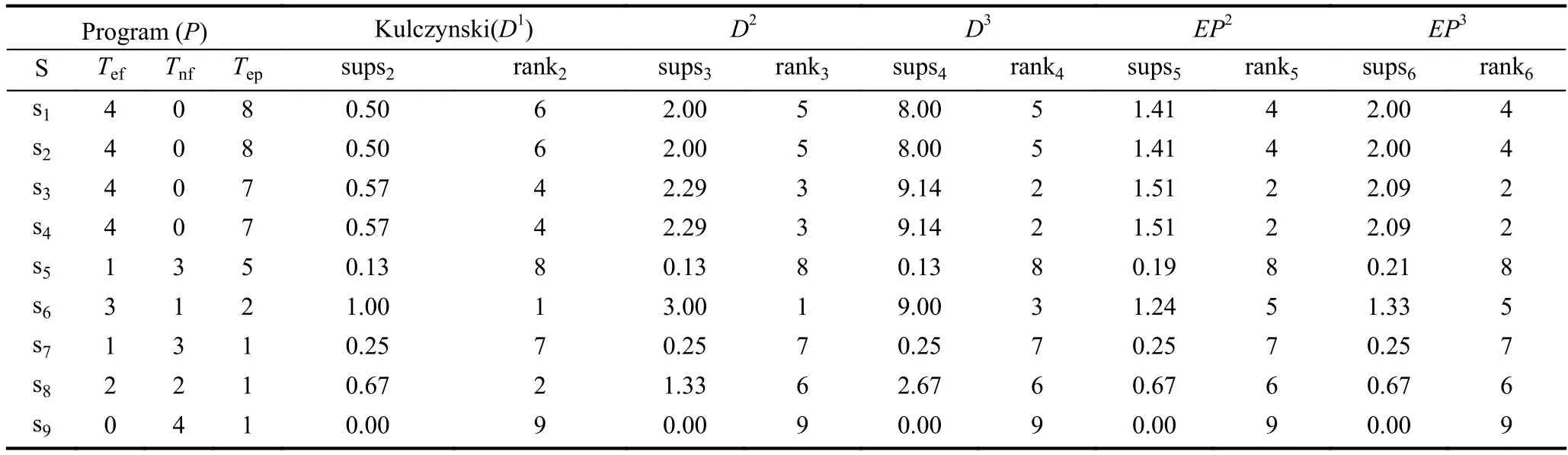
表2 可疑值計算對比表

基于上述分析， 簡要說明了本文提出的EP*方法在缺陷定位中的應用， 在該實例中，EP*方法顯著減弱了執行通過語句數Tep對可疑值的過度影響， 使其缺陷定位效果比Ochiai和D*方法好. 當系數取2時，EP*方法中的缺陷語句排名已經達到D3方法的缺陷語句排名，從中可以看出，EP*方法比D*方法收斂更快. 在下一節中將通過實驗對比分析EP*缺陷定位方法與其他缺陷定位方法的實驗結果.

2 實驗

本節首先介紹目標程序信息， 再通過實驗說明EP*方法的缺陷定位效果.

2.1 測試程序集

實驗使用了SIR中的Siemens suite測試套件和space 程序[22]， Siemens suite 包含 7 個程序， 它是由實現不同功能的C 程序組成， 每組程序通過人工注入的方式植入缺陷. space程序測試包含的多個版本都是實際的缺陷， 其詳細信息如表3所示. 表3中各列分別表示程序名、每個程序缺陷版本數、程序代碼行數、測試用例個數、程序功能的簡要描述. 該測試集涉及各種缺陷類型， 以模擬實際可能存在的缺陷. 本實驗用到了Siemens suite測試套件中的121個版本和space程序的20個版本. 其中， 去除某些缺陷版本的原因有:“Core dumped”錯誤無法生成覆蓋文件、宏定義錯誤和頭文件缺陷等.

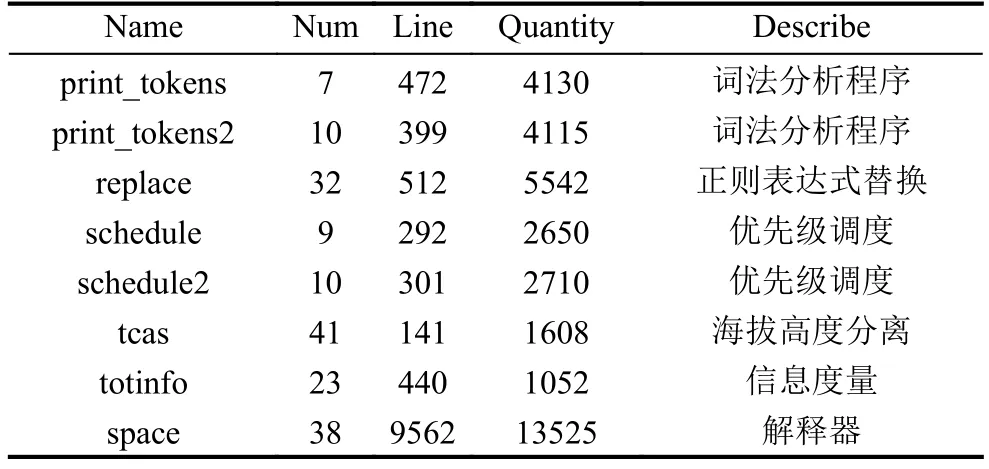
表3 實驗程序信息

2.2 缺陷定位評測指標

基于語句排名的評測采用了Score評測指標. 按照可疑值Suspiciousness的取值從高到低進行排序， 值越高代表該語句為缺陷語句的可能性越大， 反之， 則代表該語句是缺陷語句的可能性越小. 假設排查程序P={s1，s2，…，sn}， 其中 sf為缺陷語句，n為程序 P 的語句數.衡量缺陷定位方法優劣的指標是看在該方法中， 按可疑率排序缺陷語句被檢查到的位序(Rank). 當存在m(m＞0)個語句與缺陷語句sf的可疑值取值相等時， 目前有兩種方法計算Rank值. 假設可疑值高于sf的程序語句個數為t， 則方法一: 考慮最壞情況， 即設缺陷語句的Rank=m+t， 本實驗采用該方法計算Rank值； 方法二:考慮平均情況， 即設缺陷語句的Rank=t+m/2. 基于缺陷語句的Rank值， 常用的評測指標為Score如公式(2)所示， 其表示不用檢查的語句占所有語句的百分比.Score值越高， 則說明程序員在缺陷定位時不用檢查的語句越多， 需要檢查的代碼行數越少， 也就說明了缺陷定位的效果越好， 反之， 則說明缺陷定位方法效果差.

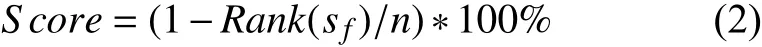
3 實驗分析

為了能夠清晰對比本文所提出的缺陷定位方法EP*對缺陷定位的影響， 本節通過實驗對比Tarantula方法、Jaccard方法、Ochiai方法和D*方法的Score評價指標來說明該方法的有效性， 實驗設置系數(*)分別為3、5和10. 表4是基于西門子套件的每個分數范圍運行百分比， 而表5是基于space程序的每個分數范圍運行百分比.

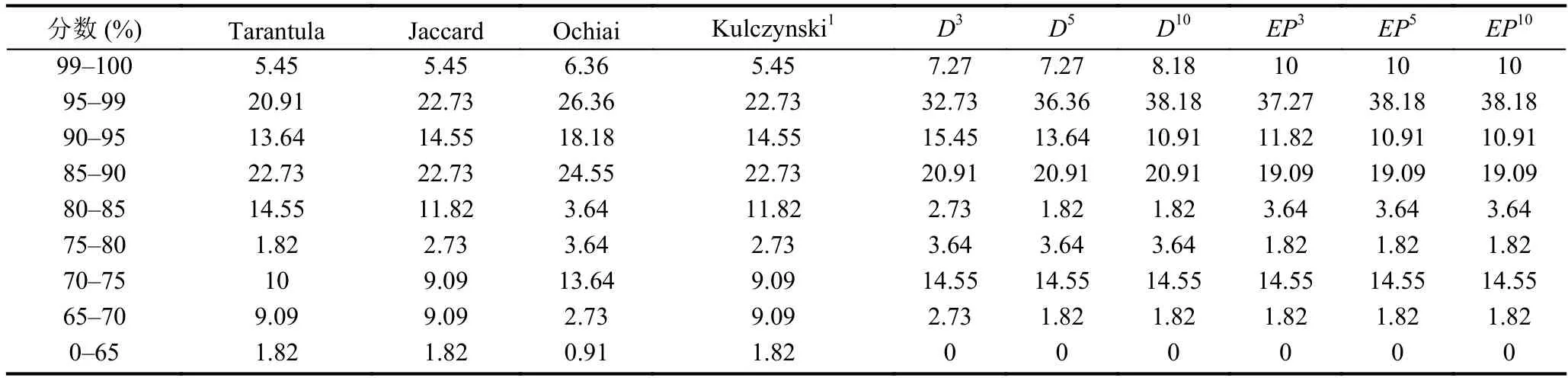
表4 西門子套件中的每個分數范圍運行百分比

從表 4 中可以看出，D3、D5、D10、EP3、EP5和EP10的所有缺陷語句均能在不用檢查的語句占所有語句的 65% 內被發現， 但Tarantula、Jaccard、Ochiai和Kulczynski1在檢查35%代碼后還有少部分缺陷語句是無法排查到. 查看Score在99-100%區間內， 即， 檢查代碼數量在1%內便可確定缺陷代碼位置的情況. 其中EP3、EP5和EP10在檢查代碼數量的1% 內可排查缺陷占 10%， 分別比Kulczynski1、Jaccard、Tarantula、D10、D5、D3、Ochiai的準確率提升了 4.55、4.55、4.55、1.82、2.73、2.73、3.64 個百分點. 圖1(a)對應于表4數據， 表示基于西門子套件的Score值的缺陷定位效果對比圖. 從圖中可以發現EP3、EP5和EP10曲線均在其它方法的曲線上面， 然后是D10、D5和D3曲線， 最下面的曲線是Tarantula. 由此可知: 在缺陷定位效果上， 基于西門子套件中EP*方法只需檢查更少量的代碼行就可以找出缺陷位置， 即，EP3、EP5和EP10比其它方法好， 其中Tarantula方法最差.

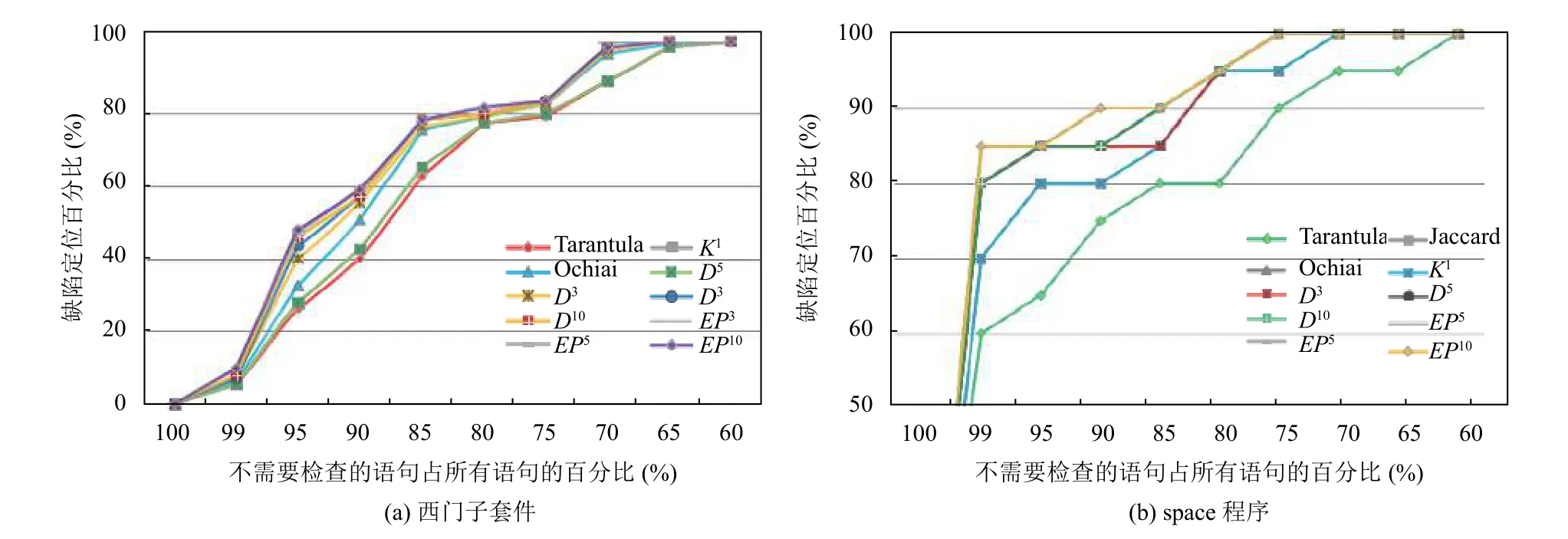
圖1 基于Score值的缺陷定位效果對比圖

從表 5 中可以看出，D3、D5、D10、EP3、EP5、EP10和Ochiai的所有缺陷語句均能在不用檢查的語句占所有語句的90%內被發現， 但Tarantula、Jaccard和Kulczynski1在檢查10%代碼后還有部分缺陷語句是無法排查到.其中EP3、EP5和EP10在檢查代碼數量的 1% 內可排查缺陷占 85%， 比D10、D5、D3和Ochiai提升了5個百分點； 比Kulczynski1和Jaccard準確率提升了15個百分點； 比Tarantula準確率提升了25個百分點. 圖1(b)對應于表5數據， 表示基于space程序的Score值的缺陷定位效果對比圖. 從圖中可以發現EP3、EP5和EP10曲線均在其它方法的曲線上面， 然后是D10、D5和D3曲線， 最下面的曲線是Tarantula. 由此可知: 在缺陷定位效果上， 對space程序，EP*方法只需檢查更少量的代碼行就可以找出缺陷位置， 即，EP3、EP5和EP10比其它方法好， 其中Tarantula方法最差.

從收斂性上分析表4數據， 分數范圍運行百分比為99%時EP3、EP5和EP10已經收斂達到最佳定位效果Score值為 10， 但D3、D5和D10的Score值分別為7.27、7.27 和 8.18， 顯然比EP*低. 再查看Score值在90～100%之間的情況(即發現缺陷需檢查代碼在10% 范圍內)，EP3、EP5和EP10值均達到 59.09， 而D3、D5和D10的值分別為55.45、57.27和57.27. 從中可以明顯看出， 隨著系數增大，EP*比.D*更快接近最佳定位效果. 所以EP*方法的收斂性比D*方法好.

通過上述實驗及分析可以發現， 在目標測試程序中，EP*方法表現出很好的缺陷定位效果， 比現有的缺陷定位方法都要好很多.

4 結果與展望

通過實驗發現， 基于EP*的缺陷定位方法有利于提高缺陷定位效果， 實驗結果表明，EP*方法的缺陷定位效果比現有的方法好， 而且能夠有效調整成功執行用例數， 以避免成功用例數量對缺陷定位效果的影響.