信號與系統教學淺探

祝常健 張紅

摘要：信號與系統是電子信息類專業學生在大學階段的基礎專業理論課。這門課主要學習如何使用科學的方法描述生活中的信息以及信號的分析和處理過程。課程內容是學生從中學階段的被動式學習過渡到高等教育階段的主動式學習的關鍵節點，包含了培養學生進行更高層次的科學理論學習和培養具備科學理論創新能力的基礎理論知識。然而，在這門課的教和學的過程中一直存在很多的問題，使得很多大學生沒有及時掌握這門課的內容，為后續的知識學習造成了困難。為了使學生能夠快速地接受和掌握該門課程內容，文章從信號與系統課程內容特點分析和探討這門課的一些教學思路。

關鍵詞：信號和系統;時域;頻域;傅里葉變換;拉普拉斯變換

中圖分類號：G642.41? ? ?文獻標志碼：A? ? ?文章編號：1674-9324（2019）49-0219-04

一、引言

信號與系統是一門電子信息類專業的基礎理論課程。信號與系統主要是學習如何使用科學的數學方法描述生活中的信息。課程內容是學生從中學階段的被動式學習過渡到高等教育階段的主動式學習的關鍵節點，包含了培養學生進行更高層次的科學理論學習和培養具備科學理論創新能力的基礎理論知識。特別是在進行科學研究的時候，信號與系統是最基礎的知識和方法。其中的知識可以延伸應用到其他的學科領域，比如機械、控制、化學、材料學和生物等。信號與系統中的許多知識，比如沖激函數和頻域分析（傅里葉變換）方法，不僅僅是一個描述生活信息的數學工具，更是一種可以徹底顛覆一個人以前世界觀的思維模式。但是，信號與系統的數學公式大部分看起來太復雜了，所以很多初學者乍一看就懵圈并從此對它深惡痛絕。如此重要的課程知識，信號與系統居然成了現在大部分高校學生學習的殺手課程。

為了讓學生在學習信號與系統過程中不再是枯燥難學的感覺，讓學生快速地掌握這門課程，國內的許多高校教師進行了這門課的教學方法的探索[1]。高燕教師在文獻[2]中，討論以創新人才培養為目的的信號與系統教學方法改革和研究。筆者主要是深度結合MATLAB軟件的應用，該軟件具有良好的數學矩陣運算功能，能夠把信號與系統復雜的數學運算用MALTAB代碼簡單明白地展示。同時還結合計算機網絡輔助教學，提高學生的積極性和學習信號與系統的手段的多樣性。文獻[3]中，以黃山學院為實踐教學，根據信號分析與處理課程群建設要求優化教學內容，構建線上、線下和項目驅動方式的教學模式。蔡凡在文獻[4]中，探索了面向應用型人才培養的信號與系統的教學方法。謝自梅研究了基于MATLAB作為教學平臺，為學生提供一個輕松愉快、高效的學習氛圍[5]。類似的角度在文獻[6]中也有研究。方偉偉等人基于“雨課堂”研究信號與系統的教學方法，提高學生學習過程中注重預習和提高教學過程中的師生之間交互效率[7]。劉淑玉等人將信號與系統的教學內容與網絡分析、數字信號處理、隨機信號等課程內容結合起來，合理地安排該門課程的教學內容。筆者還把多媒體教學和傳統教學相結合，探索一種讓學生系統地吸收信號與系統的教學方案[8]。高諾等人從實驗教學的角度對信號與系統的實驗教學的體系和內容安排等三個方面進行探索，目的是為了培養學生的學習興趣、工程實踐素養和創新思維等方面的能力[9]。苗丹結合應用型本科院校的特點，從如何培養學生的應用實踐能力角度研究信號與系統的教學[10]。另外，呂軍等人在文獻[11]中提出直觀化教學的概念，以提高教學質量和調動學生學習的積極性。

以上的研究成果主要是從教學內容和實驗教學角度探索如何提高信號與系統的教學質量和效率。這些研究成果都從比較嚴肅的角度出發，始終存在讓學生無法輕松愉快地接受和掌握信號與系統的知識，還沒有一個完整、高效和嚴謹的教學方案。為了從讓學生更加輕松和充滿樂趣地學習信號與系統，本文結合在電子信息工程專業學習的教學和學習體會，嘗試從知識的特點和教學內容的展示方式上探討信號與系統的知識講授方法。

二、課程內容分析

信號與系統是學習信息的描述和處理的工程數學。學習的內容主要是如何建立信息的數學模型，如何處理、分析和研究信息/信號。需要具備的學科知識是微積分、模擬電路、數字電路等課程。在這門學科的發展過程中，許多數學家和科學家，如讓·巴普蒂斯·約瑟夫·傅里葉、拉普拉斯和香農等都做出了重要的貢獻。

（一）信號的描述方法

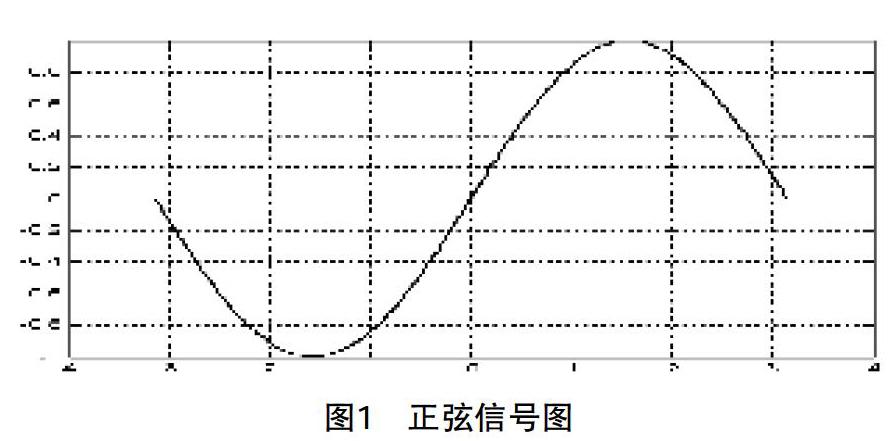
信號與系統主要是學習如何使用科學的數學方法描述世界的信息。描述信息的方法主要有圖形曲線和函數表達式。曲線主要是指描述信號變換形狀的劃線，比如正弦和余弦曲線，如圖1所示。函數表達式主要是對信息用數學的方法描述，s（n），f（t）等，比如圖1中正弦曲線可以表示為y=sin（2πt）。因此，在學習信號與系統的過程中，必須掌握圖形曲線和函數表達式的相互對應轉換，給出信號可以用劃出曲線，同時能夠寫出對應的函數表達式。

再者，必須掌握信號的分析，周期信號和非周期信號、連續信號和離散信號等分類。在這些常見的函數的基礎上，特別是必須掌握奇異函數的表達式子，即沖擊函數和階躍函數。

（二）系統的概述

在對世界的信息進行描述而得到信號后，需要對信號進行處理。那么，信號處理的過程就是系統。信號的產生、傳輸和處理需要一定的物理裝置，這樣的物理裝置通常稱為系統。一般而言，系統（system）是指若干相互關聯的事物組合而成具有特定功能的整體。如手機、電視機、通信網、計算機網等都可以看成系統。它們所傳送的語音、音樂、圖像、文字等都可以看成信號。信號的概念與系統的概念常常緊密地聯系在一起。系統的基本作用是對輸入信號進行加工和處理，將其轉換為所需要的輸出信號，如圖2所示。在學習的過程中需要掌握系統的輸入和輸出之間的關系。

（三）信號的變換域

信號與系統中最重要的一個內容就是信號的變換域。在我們日常生活中，我們看到的世界都是以時間作為衡量標準，事情的變化、樹木的生長、人的位置的變化都會隨著時間發生改變。這種以時間作為參照來觀察動態世界的方法稱其為時域分析。在隨著時間不停變換的過程中，我們很難分析信號的特性。因此，科學家們找到了一種變換域，即頻域。我們發現在頻域中，世界是永恒不變而且具備一定的特點，這樣便于分析和處理信號。在我們的日常生活中，普遍認為世間萬物都在隨著時間不停地改變，并且永遠不會靜止。因此，在學生學習變換域這部分內容的時候，根本無法接受，更別說理解了。而這一部分內容是信號處理以及后續課程數字信號處理的核心內容。如果這部分內容沒有學習好，根本無法掌握信號與系統的內容。

對于頻域，先說一個最直接的用途，就是廣播收音機的頻段，在收音機接收信號的時候，不同的電臺使用的是不同的頻道。這里的頻道就是不同頻段的信道，這里的信道用來傳輸不同的信息。那么信號的頻域有優點呢？我們可以從一個例子開始比如先在紙上畫一個sin（x），我們可以很容易畫出近似的正弦信號圖，如圖1所示。接著，如果要求在紙上用筆畫一個

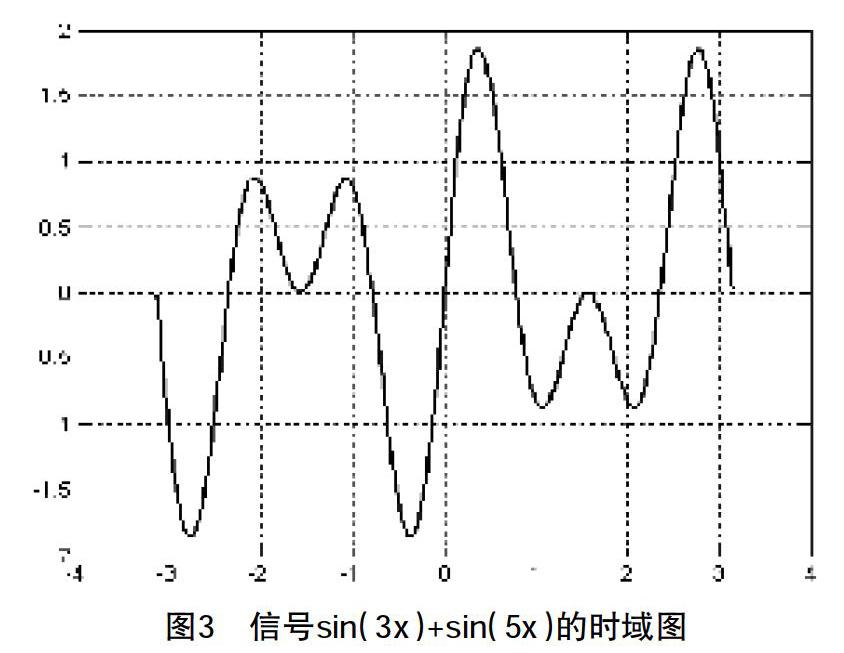
f（x）=sin（3x）+sin（5x）的圖形，我們發現根無法完成，因為曲線什么時候上升和下降，我們根本無法畫出來。而用MATLAB畫出來的f（x）=sin（3x）+sin（5x）的曲線如圖3所示。如果再進一步要求，假設我們不知道這個曲線的方程式，現在需要把sin（5x）從圖3里拿出去，看看剩下的是什么？我們發現，在時域中這基本是不可能做到。

但是在頻域呢？把信號f（x）=sin（3x）+sin（5x）做傅里葉變換后得到的頻譜圖就是幾條豎線而已如圖4所示，很容易就可以把不同的信號的譜線找出來，以及可以濾去剩下我們想要的信號。所以很多在時域看似不可能做到的數學操作，在頻域很容易，這就是需要傅里葉變換的地方。尤其是從某條曲線中去除一些特定的頻率成分，這在工程上稱為濾波，是信號處理最重要的概念之一，只有在頻域才能輕松做到。

三、知識點的展示方式分析

通過教學活動我們發現，知識的傳授很講究知識點的展示方式。有時候復雜枯燥的數學公式，可以使用生活中一個簡單的例子說明白，或者是使用一個形象的圖來展示，提高教學的質量。

（一）結合生活例子解釋概念

信號與系統的理論知識其實也是源于生活。在進行教學活動的時候，不能夠脫離生活中的應用純粹講授數學公式，那樣會大大降低教學質量。因此在教學活動中，在一些知識點的講授過程中，可以適當舉一些生活中的例子。例如，我們講授信號、系統的定義的時候，可以舉手機信號發射和接收的例子。如圖5所示，手機會采集生活中的信息，包括文字、圖片、語音、視頻等，然后經過手機的處理就發射出去，在另外的接收端手機就會接收下來處理，再顯示。手機拍攝的人、大樓、樹、汽車等世界中的各種事物和事情就是信號，兩部手機一發送一接收就是一個完整的系統。通過舉這樣的生活中的手機例子，就可以把信號與系統的定義講述清楚。

（二）結合圖形的知識內容展示

對于一門工程數學，無論是在講授信號的內容還是系統的內容的過程，我們發現都是一些繁雜的數學公式。那么我們應該想辦法，盡可能地把這些數學公式的知識點用一些簡單易懂的圖形來描述。比如在講授傅里葉變換的定義的時候，公式的表達就是

以上就是完整的傅里葉變換公式，如果直接講述這兩個公式的字面意思，很多學生根本無法理解傅里葉變換的物理意義，也不知道什么是傅里葉變換。先舉個例子：在我們的理解中，一段音樂是什么呢？

我們對音樂最普遍的理解是，音樂是一個隨著時間變化的震動。但我們相信，對于樂器手們來說，音樂更直觀的理解是一個個的音符圖。具體為在時域，我們觀察到鋼琴的琴弦一會上一會下地擺動，就如同波浪的走勢;而在頻域，只有那一個永恒的音符，也就是一個基本的余弦信號。傅里葉變換理論告訴我們，任何周期函數都可以看作不同振幅、不同相位正弦波的疊加。這樣對于任意的音樂信號，我們可以理解為利用對不同琴鍵不同力度、不同時間點的敲擊，可以組合出任何一首樂曲。

類似地，任何信號都是由一組基本的正弦波組成，隨著正弦波數量逐漸地增長，它們最終會疊加成一個信號。隨著疊加的遞增，所有正弦波中上升的部分逐漸讓原本緩慢增加的曲線不斷變陡，而所有正弦波中下降的部分又抵消了上升到最高處時繼續上升的部分，使其變為水平線。我們能想到的任何波形都是可以用正弦波疊加起來的。這是沒有接觸過傅里葉分析的人在直覺上的第一個難點，但是一旦接受了這樣的設定，后面的學習就開始變得有趣起來了。比如信號的頻譜都是通過多個正弦信號的疊加，從頻率軸觀察得到，如下頁圖7所示。

在圖中，最前面顯示的頻譜線就是所有正弦波疊加而成的總和。它是由多個正弦信號在后面依不同顏色排列而成的，正弦波就是組合為這個信號的各個分量。這些正弦波按照頻率從低到高從前向后排列開來，而每一個波的振幅都不同，從而構造成任意的信號。基于以上的展示，我們可以發現頻譜其實就是信號疊加圖，從另外一個角度看得到的圖形，從頻域方向看到的就是頻譜。這樣比純粹用數學公式解釋的傅里葉變換要直觀得多。

四、總結

本文以結合圖形方法和生活例子的內容展示方式初步探討信號與系統的教學方法。目的是避免枯燥的數學公式給初學者造成的學習的困難，以更加快樂和高質量地掌握信號與系統的知識，從而提升學生學習信號與系統及其相關科目的興趣，克服畏懼心理，做到真正掌握信號與系統相關知識，為進一步深造打下堅實的理論基礎。

參考文獻：

[1]陳萬培，儲誠明，胡學龍，等.獨立學院電子信息工程專業人才培養模式的實踐[J].工業和信息化教育，2013，（1）.

[2]高燕.以創新人才培養為驅動的信號與系統課程改革研究[J].中國教育技術裝備，2017，（22）：42.

[3]呂軍，寧仁霞，孫劍，等.面向應用型人才培養的信號與系統課程教學改革研究——以黃山學院為例[J].黃山學院學報，2017，（05）：122-125.

[4]蔡凡，朱同波.基于應用型人才培養的“信號與系統”課程改革與探索[J].收藏，2018，（1）：92.

[5]謝自梅，范黎林.基于MATLAB的促進師生共同發展的《信號與系統》課程教學改革[J].教育教學論壇，2018，（11）：103-107.

[6]王俠，顧明亮.MATLAB在《信號與系統》課程中的應用[J].中國科技信息，2007，（12）：248-249.

[7]方偉偉，李鑒，黃照光，等.基于“雨課堂”的《信號與系統》課程教學改革實踐[J].現代計算機：上下旬，2017，（17）：25-28.

[8]劉淑玉，趙偉，胡明華.關于電類方向信號與系統課程全面改革的幾點措施——知識體系的完善與習題，實驗的改進[J].科教文匯，2017，（2）：63-65.

[9]高諾，耿淑娟，楊紅娟.“信號與系統”實驗教學改革探索與成效[J].教育教學論壇，2017，（19）：152-153.

[10]苗丹.《信號與系統》課程教學改革研究與實踐[J].教育教學論壇，2017，（40）：166-167.

[11]呂軍，孫劍，寧仁霞，等.信號與系統課程直觀化教學方法的探索與實踐[J].科技視界，2017，（16）：26-26.