組合后通過平移或旋轉實現密鋪的凹五邊形研究

郝四柱

(南京金陵中學仙林分校中學部 210000)

1 問題提出

據外媒報道，美國華盛頓大學研究團隊近日發現了一種新的不規則凸五邊形，相互組合后可完全鋪滿平面，不會出現重迭或空隙，是全球第15種能做到此效果的凸五邊形(如圖1).而距上次發現類似效果的凸五邊形已時隔30年，這項發現相當于在數學領域中尋獲了新原子粒子.[1]它們的方法是“把12個全等的該五邊形組合成圖2的形如海馬狀圖形，然后把海馬狀組合圖進行平移，形成圖3的密鋪圖案.”

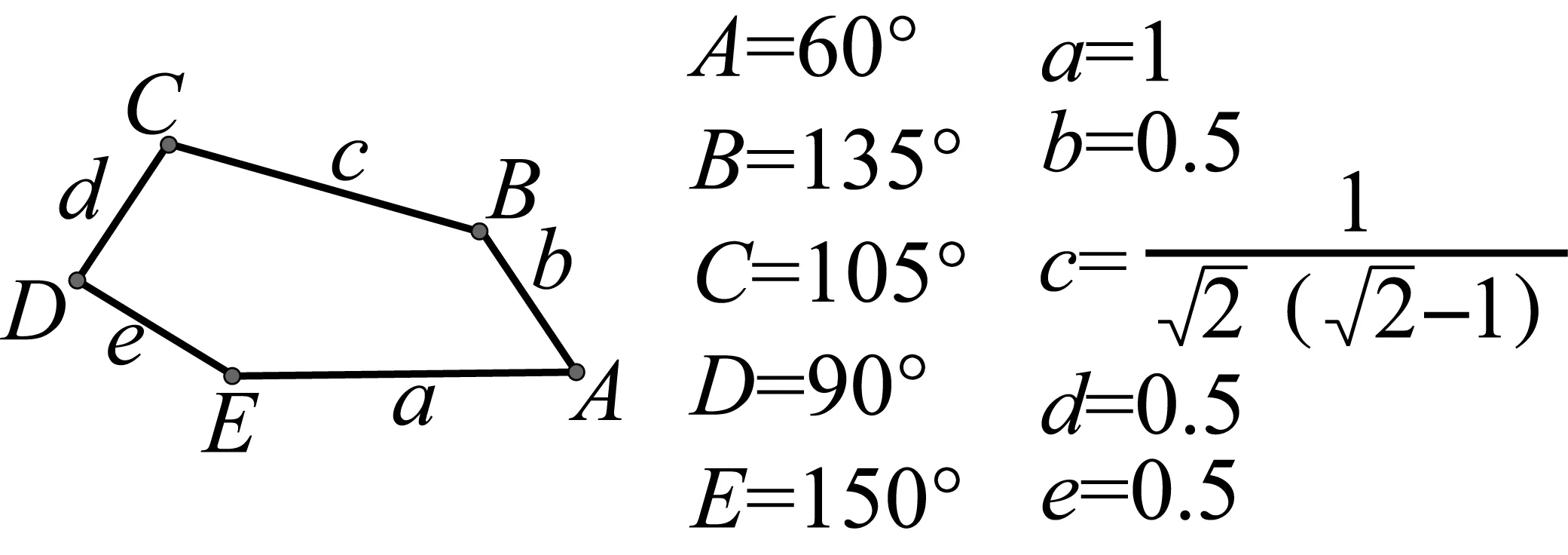
圖1

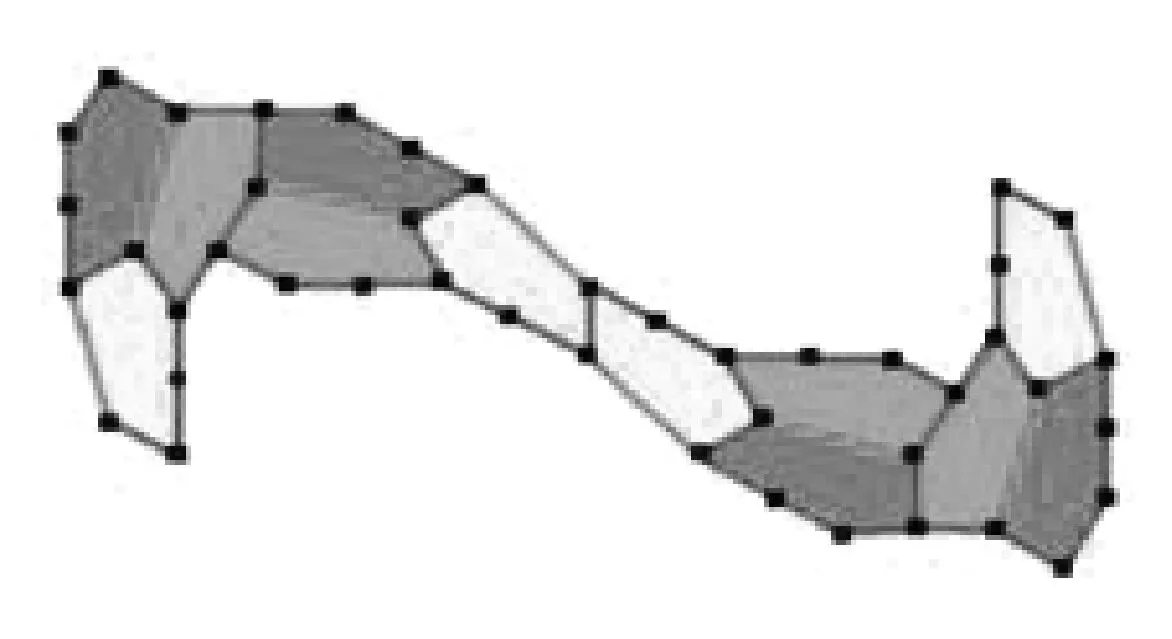
圖2

圖3

所謂的平面密鋪也就是鑲嵌，即，用平面圖形完全覆蓋一個二維平面，而且圖形之間沒有重疊；其中，只用一種全等圖形的密鋪，我們稱之為單密鋪.眾所周知，1.由全等的三角形單密鋪可以鋪滿整個平面；2.由全等的四邊形單密鋪可以鋪滿整個平面(含凹四邊形)；3.正五邊形由于每個內角為108°，所以不能密鋪整個平面.那么，其它的不規則五邊形單密鋪問題成為人們研究密鋪的一個焦點.

由于人們對于凸五邊形密鋪研究有了一些成果，那么凹五邊形呢？目前還不多.所以本文探討凹五邊形的單密鋪問題：“只用一種全等凹五邊形，形成一種組合圖形，然后把組合圖形通過平移或旋轉實現平面密鋪.”

2 凹五邊形通過組合，得到基本組合圖形，該基本圖形可以通過平移實現密鋪

筆者從已有的凸五邊形密鋪方法入手，進行凹五邊形的密鋪的對比研究，結合正多邊形特點、黃金三角形特點以及幾何圖形的相關知識的研究，得出結論如下：

(1)具有兩邊平行的凹五邊形，組合后的基本組合圖進行平移實現密鋪

基本圖基本組合圖密鋪圖第1種情況∠B+∠C=180°,∠A+∠ D+∠E =360°(其中內角∠E大于180°)

(2) 通過正多邊形的結構分解獲得的凹五邊形；這類正多邊形必須可以進行平移實現密鋪，從而實現凹五邊形的密鋪

由于正方形和正六邊形是簡單而優美的圖形；并且都可以通過平移獲得整個平面的密鋪，所以通過對于正方形、正六邊形的研究獲得能夠密鋪的凹五邊形.①將正方形分割成4個全等的凹五邊形.其密鋪的圖案如下第2種情況.②將正六邊形分割成6個全等的凹五邊形.其密鋪圖案如下第3種情況.

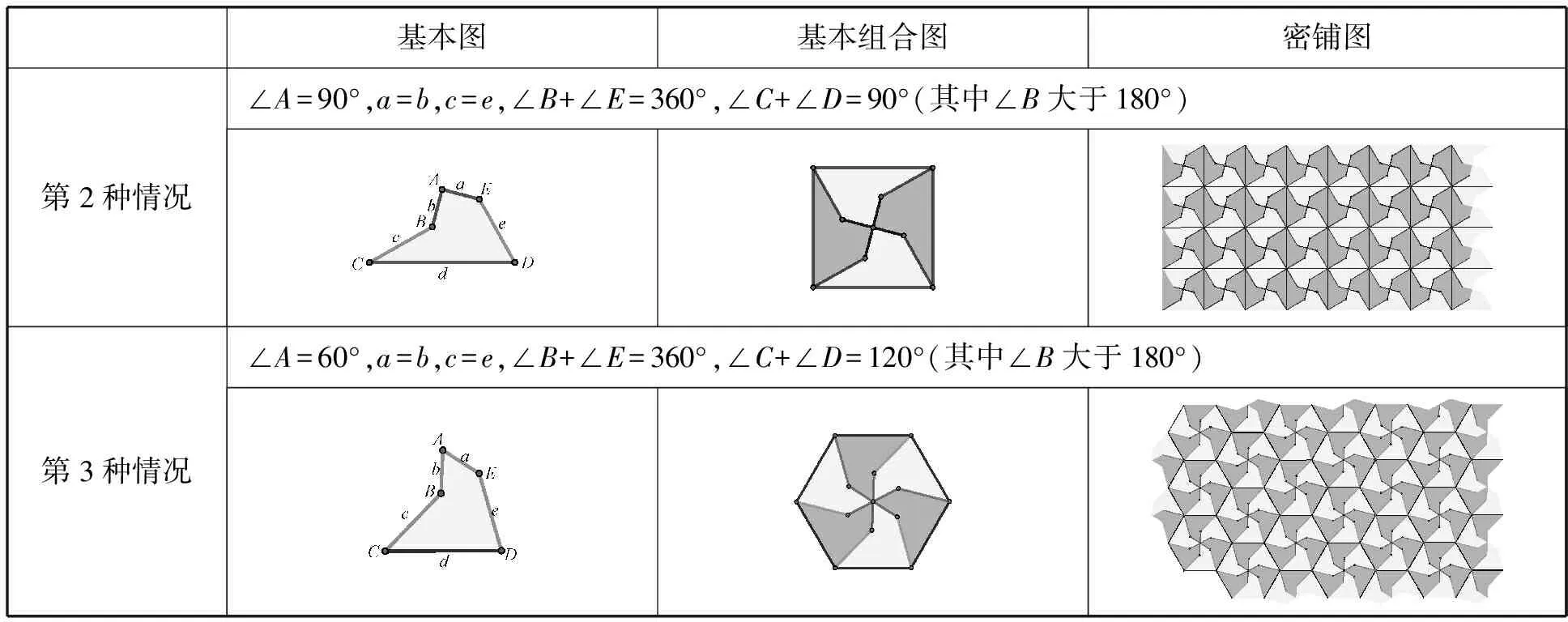
基本圖基本組合圖密鋪圖第2種情況∠A=90°,a=b,c=e,∠B+∠E=360°,∠C+∠D=90°(其中∠B大于180°)第3種情況∠A=60°,a=b,c=e,∠B+∠E=360°,∠C+∠D=120°(其中∠B大于180°)

(3) 內角均為36°倍數的凹五邊形，組合后的基本組合圖可以進行平移實現密鋪[2]

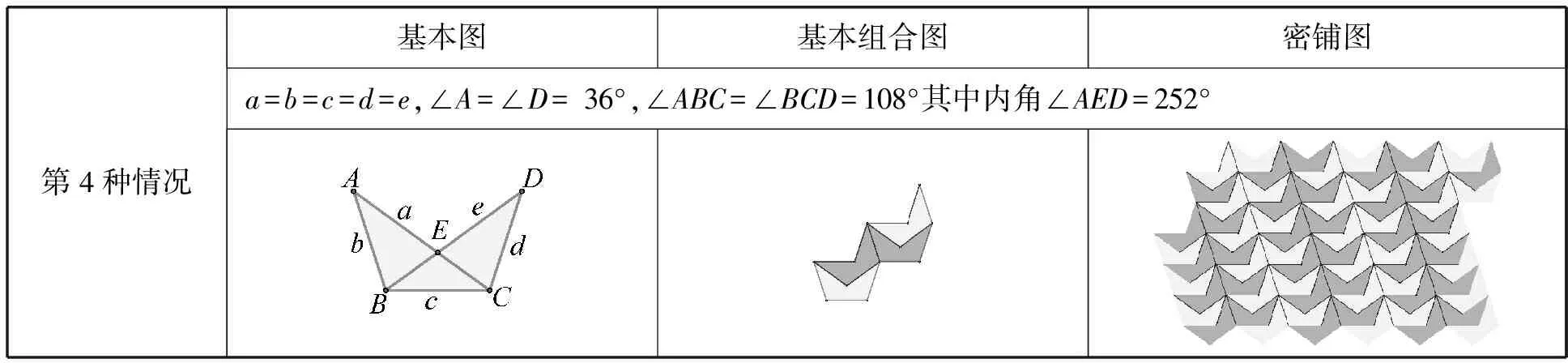
第4種情況基本圖基本組合圖密鋪圖a=b=c=d=e,∠A=∠D= 36°,∠ABC=∠BCD=108°其中內角∠AED=252°

(4)四條邊相等的凹五邊形進行組合，組合后的基本圖形可以進行平移實現密鋪

(5)兩邊或三邊相等的凹五邊形組合，組合后的基本組合圖可以進行平移實現密鋪

基本圖基本組合圖密鋪圖第8種情況b=d,c=e,∠B+∠D=180°;(其中內角∠A大于180°,隱含條件是:∠A+∠C+∠E =360°)第9種情況b=c,d=e;∠B=∠D=90°;(其中內角∠A大于180°,隱含條件是∠A+∠C+∠E =360°)第10種情況a=b,c=d;∠A=60°,∠C=120°;(其中內角∠E大于180°,隱含條件∠B+∠D +∠E=360°)第11種情況a=d=e,b=c;∠B+∠D=180°,∠E=2∠B(其中內角∠A大于180°,隱含條件是:∠A+∠C +2∠B=360°)第12種情況d=2a=2e,∠B=∠E=90°,∠A=∠C(其中內角∠D大于180°,隱含條件是:∠D+2∠A=360°)

3 凹五邊形通過組合，得到基本組合圖形，該基本圖形可以通過旋轉實現密鋪

(一)凹五邊形組合后的基本組合圖，能實現旋轉密鋪；這樣的凹五邊形必須符合什么條件

首先有角度上的特征：因為凹五邊形旋轉一周為360°；所以凹五邊形至少有一個內角應該是360°的因數.由于360°的因數有很多，其中常見的有30°、36°、60°、72°、90°、120°.

從邊長來說，用同一種凹五邊形通過旋轉實現平面密鋪，還體現在邊長上：因為該圖形通過旋轉實現平面密鋪，必須有邊重合，所以有相等的邊長.特別地，如果五邊均相等，那么這樣的凹五邊形更容易實現旋轉密鋪.

(二)組合后的基本組合圖，能實現旋轉的單密鋪研究

(1)和黃金三角形聯系的凹五邊形

① 黃金凹五邊形的組合方式的介紹

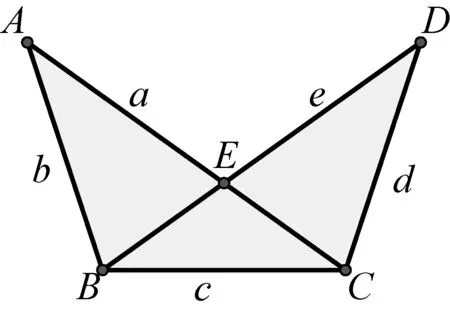
圖4

如圖4，是五邊相等的凹五邊形ABCDE，內角均為36°的整數倍，(a=b=c=d=e,∠A=∠D=36°，∠ABC=∠BCD=108°，其中內角∠AED=252°)；用這類五邊形組合后，可以通過旋轉的方法實現密鋪(如圖5).該五邊形是如何進行組合然后進行旋轉密鋪的呢？在進行旋轉密鋪之前，我們介紹一下三個關鍵的組合方法(圖6、圖7、圖8)；圖6組合是把圖4通過旋轉和軸對稱實現的，圖7的右半部分(虛線部分)和左半部分成中心對稱，這樣圖7能夠形成一個整體.

圖5

圖6

圖7

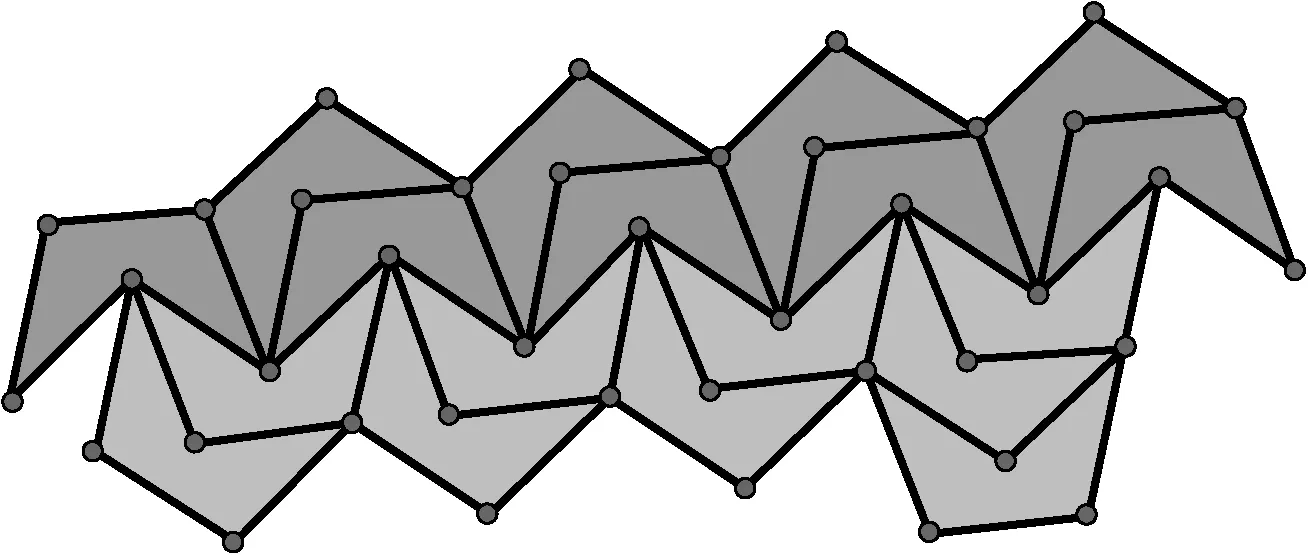
圖8

另外，圖6中下方的點A、B、C、D、E、F可以和圖7中上方的對應點(A′、B′、C′、D′、E′、F′)正好可以進行咬合，實現圖6和圖7的邊界線統一，圓滿實現密鋪(其中點B和點B′處對應的兩個角度和正好是360°(一個為72°，一個為288°)；同樣C和C′、D和D′、E和E′處均可進行咬合).

同時可以看到邊界線B′C′D′E′F′構成對稱的W型.為便于后面圖形組合的描述，我們把圖6和圖7沿W型邊界線密鋪的方法稱為咬合法.另外還有可能出現如圖8的組合方法，該方法就是把兩個相同組合，面對面扣起來.我們把這種方法叫做對扣法.對扣法中間出現一道W型的邊界線.對扣法和咬合法均是這種凹五邊形的組合方法，可以實現圖5的密鋪.

②圖5的詳細步驟見如下的(i)-(vi) 步驟

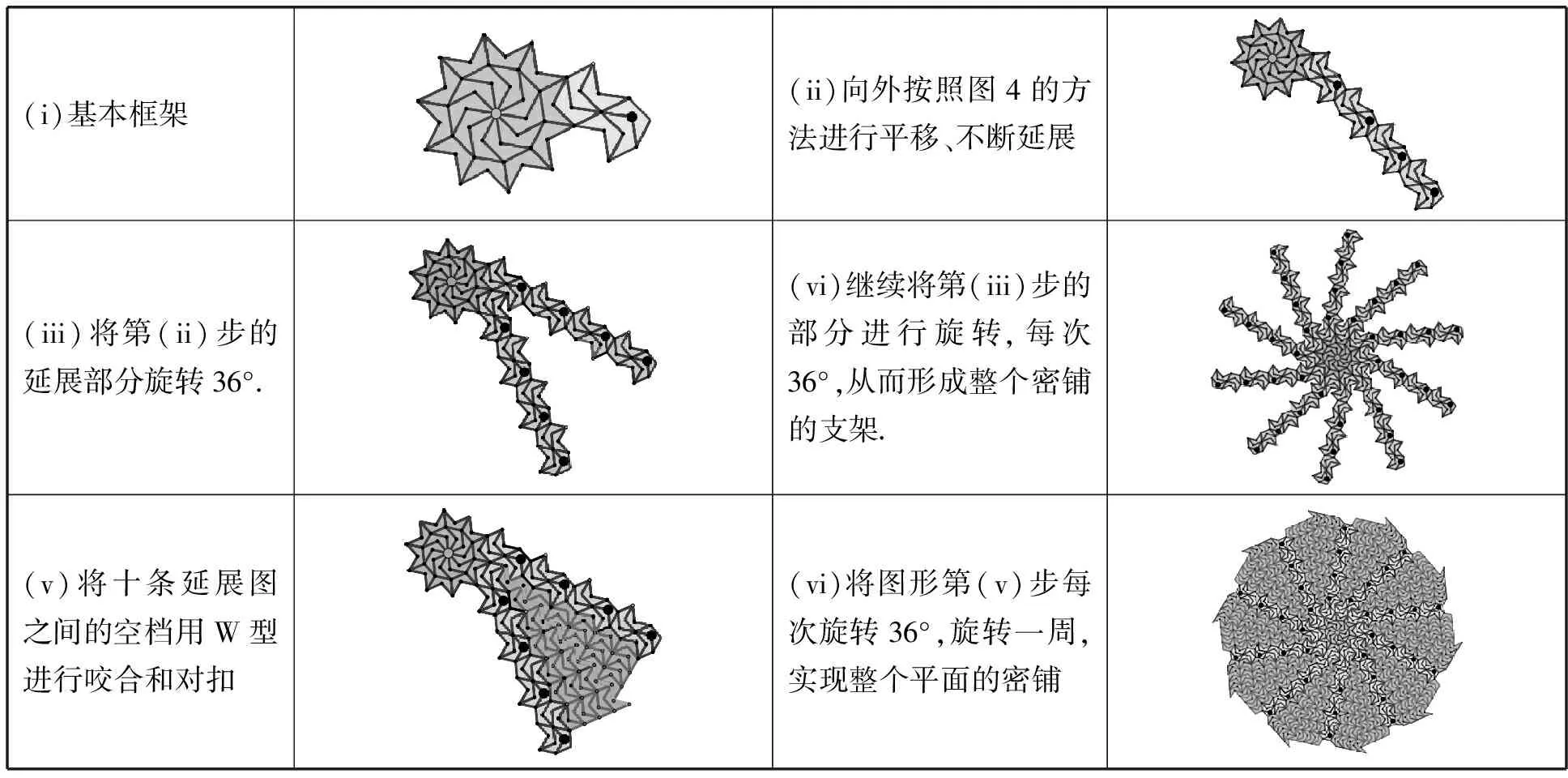
(i)基本框架(ii)向外按照圖4的方法進行平移、不斷延展(iii)將第(ii)步的延展部分旋轉36°.(vi)繼續將第(iii)步的部分進行旋轉,每次36°,從而形成整個密鋪的支架.(v)將十條延展圖之間的空檔用W型進行咬合和對扣(vi)將圖形第(v)步每次旋轉36°,旋轉一周,實現整個平面的密鋪

這里還需要強調說明的是上述的第(v)步，內部是如何密鋪的呢？首先看一下第(iii)步中，“兩條腿”邊界都是連續的W型輪廓線，我們沿著(iii)的兩條腿相對的W型輪廓線，用咬合法同時相向密鋪，內部交匯處是采用對扣的方法，其相遇處是一條連續的W曲線，近似于角平分線.從而形成第(v)步的內部密鋪.

(2)和30°、60°、90°相聯系的凹五邊形

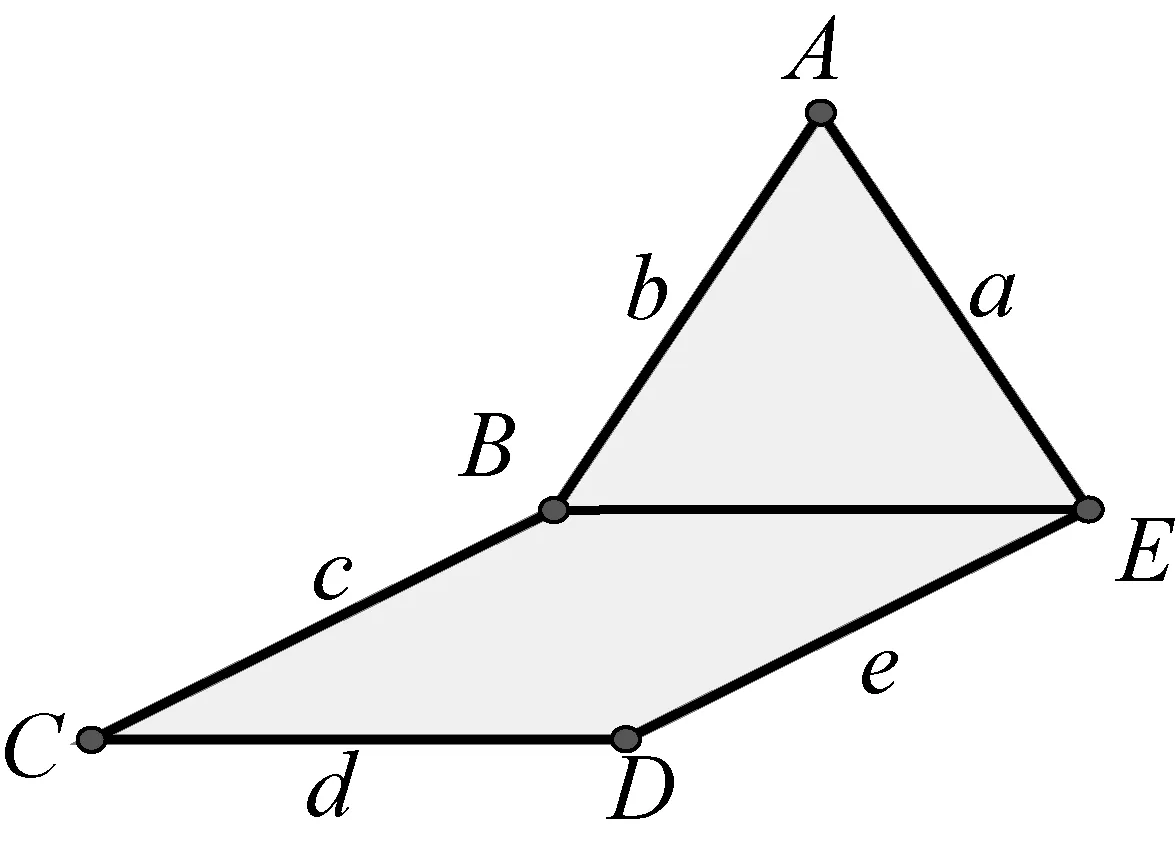
圖9

第二個凹五邊形ABCDE，如圖9，條件是：a=b=c=d=e,五個內角分別是：∠A=60°，∠ABC=210°，∠C=30°，∠D=150°，∠AED=90°,即,由等邊三角形和一個角為30°的菱形組成基本圖形.

該凹五邊形同樣可以通過旋轉實現密鋪方案如下(密鋪方法見下表)：方案一，以該五邊形的90度角的頂點為中心，90°旋轉角進行旋轉，得到正十二邊形；方案二，以該五邊形的60度角的頂點為中心，60°旋轉角進行旋轉，設計出兩種圖案，兩層正十二邊形的旋轉密鋪和三層的正十二邊形的旋轉密鋪；方案三，以該五邊形的30度角頂點為中心，30°角為旋轉角來進行旋轉，設計出四層正十二邊形旋轉密鋪圖案和五層的正十二邊形的密鋪圖案(如下表).只要愿意，三種方案均可無限向外擴展，從而實現整個平面的密鋪.

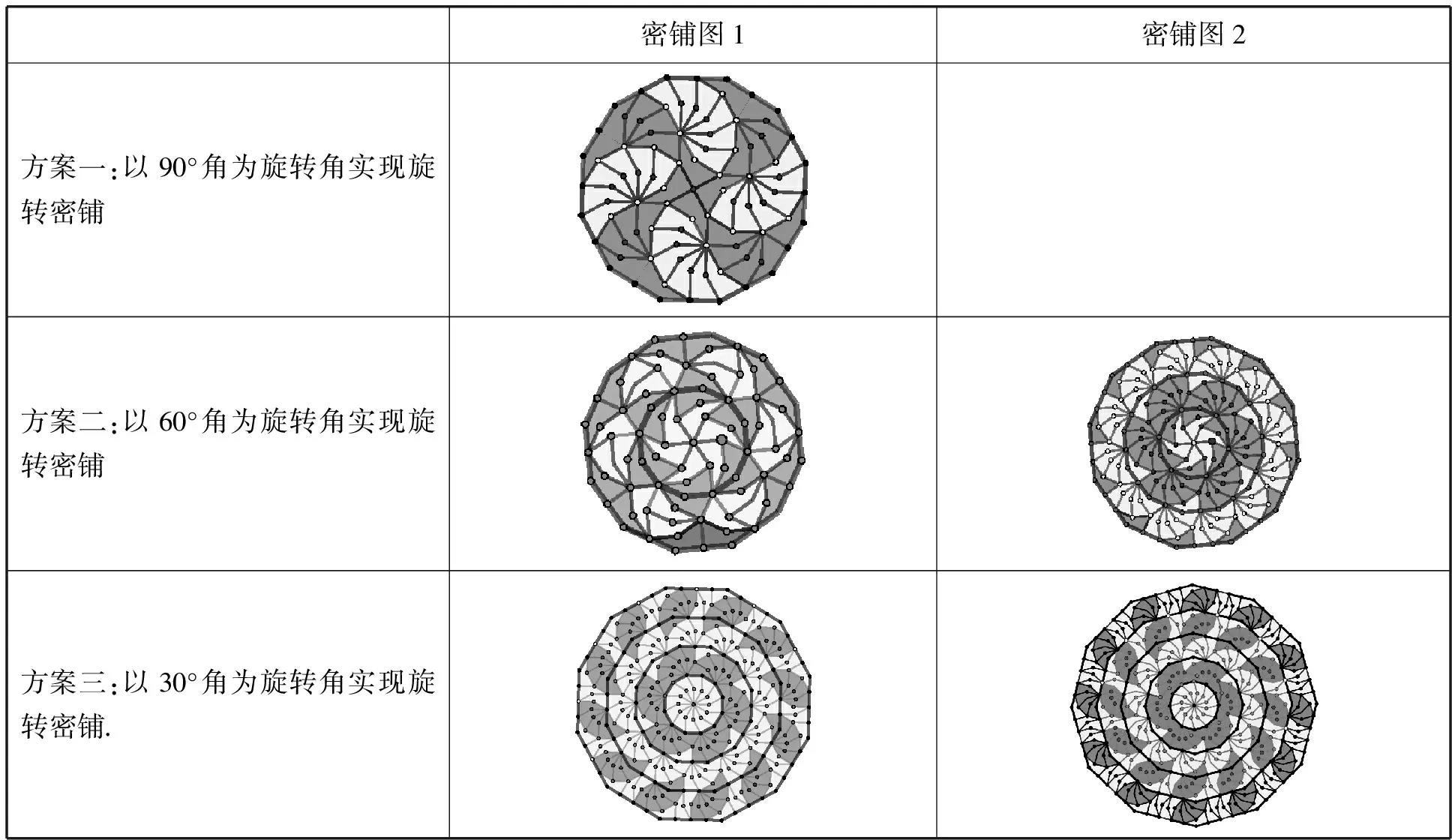
密鋪圖1密鋪圖2方案一:以90°角為旋轉角實現旋轉密鋪方案二:以60°角為旋轉角實現旋轉密鋪方案三:以30°角為旋轉角實現旋轉密鋪.

我們不妨以方案三為例：以四層的正十二邊形為基礎，如何拼出五層正十二邊形呢？進而達到更多層數的正十二邊形？操作程序如下：

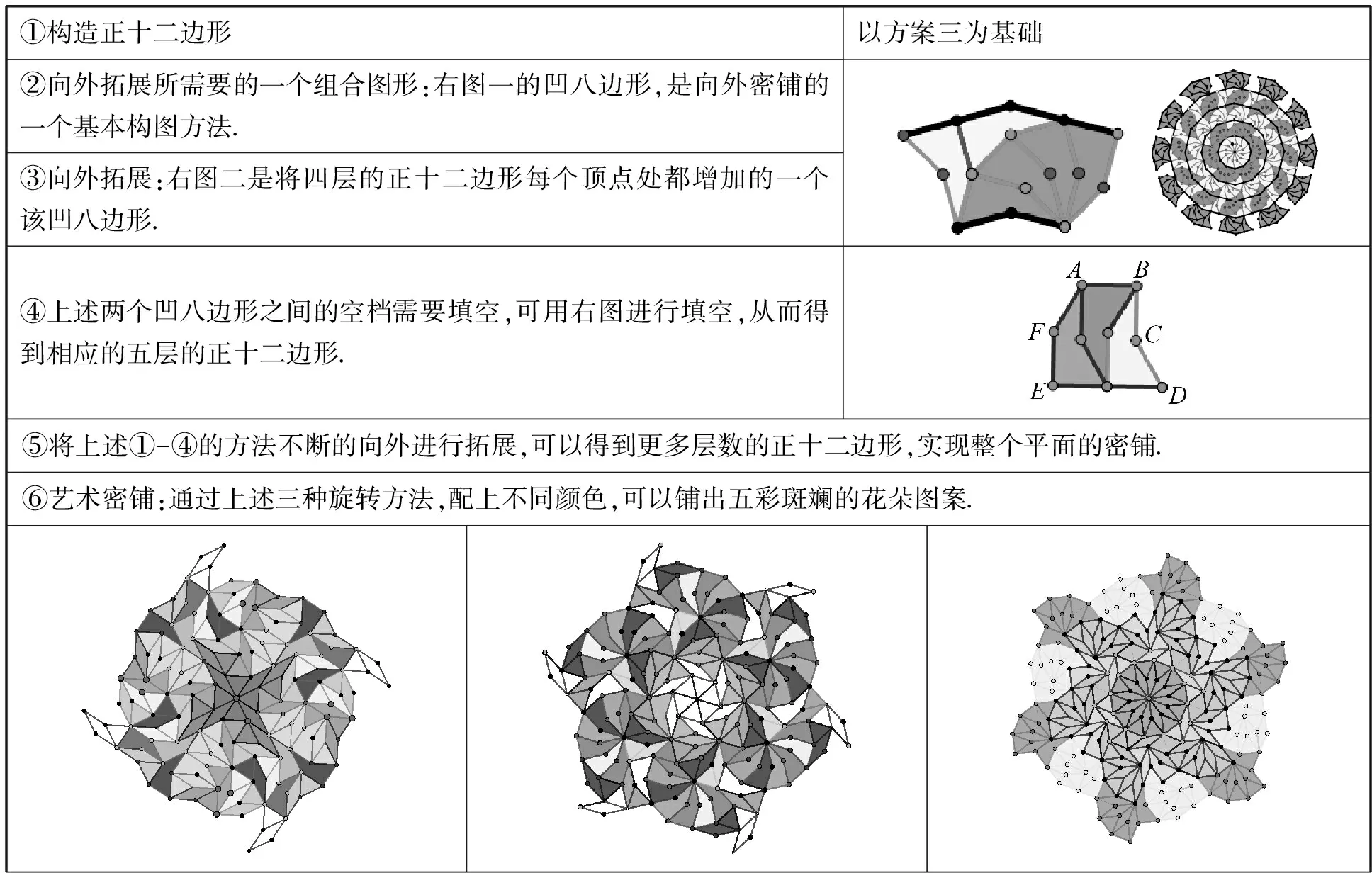
①構造正十二邊形以方案三為基礎②向外拓展所需要的一個組合圖形:右圖一的凹八邊形,是向外密鋪的一個基本構圖方法.③向外拓展:右圖二是將四層的正十二邊形每個頂點處都增加的一個該凹八邊形. ④上述兩個凹八邊形之間的空檔需要填空,可用右圖進行填空,從而得到相應的五層的正十二邊形.⑤將上述①-④的方法不斷的向外進行拓展,可以得到更多層數的正十二邊形,實現整個平面的密鋪.⑥藝術密鋪:通過上述三種旋轉方法,配上不同顏色,可以鋪出五彩斑斕的花朵圖案.

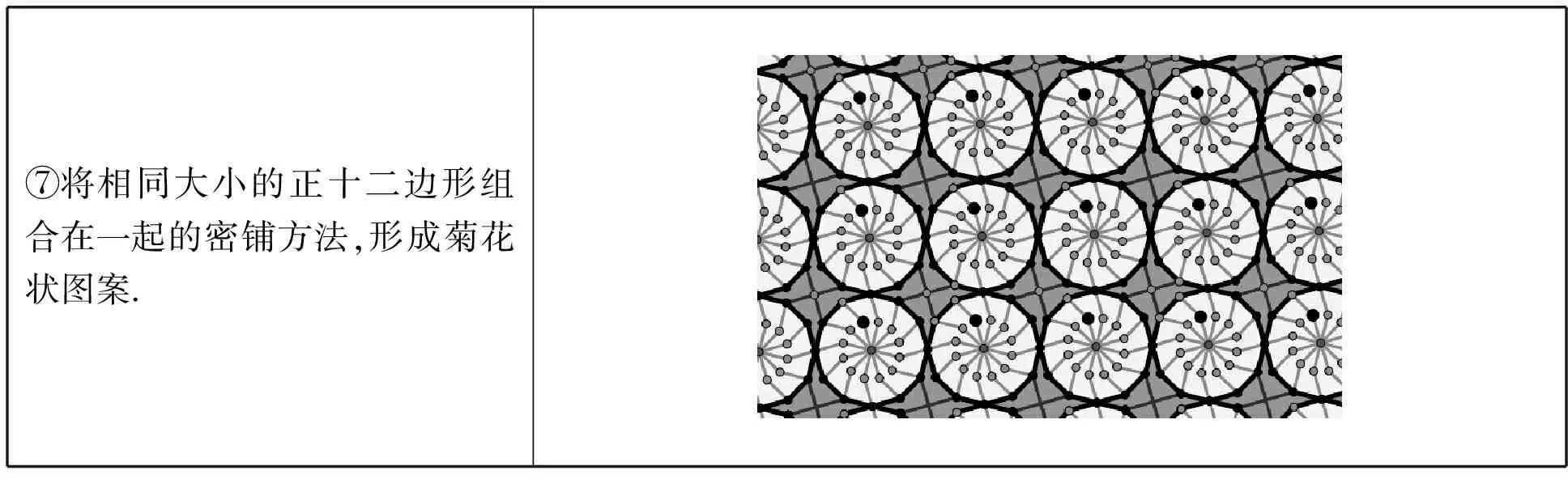
續表

綜上所述：本文所述的凹五邊形，組合后的基本組合通過平移或者旋轉這兩種變換實現密鋪；對于其他未知的凹五邊形研究可以起到啟示作用.相信隨著計算機和相關技術的進步，未來一定會有更多的能夠實現密鋪的的凹五邊形被發現.