激活問題意識 點燃思維火花
——以一道高考題的兩個教學片段為例

顧日新

(蘇州工業園區星海實驗中學 215021)

1 問題提出

隨著教育教學改革的不斷深化，培養學生的創新能力作為一個核心問題被擺到重要位置．眾所周知，創新能力的核心是創新思維，創新思維的動力是問題意識．問題意識最為顯性的表現就是敢于提出問題、敢于質疑．愛因斯坦認為：“提出一個問題往往比解決一個問題更為重要，……”；《中國學生發展核心素養》一文中也明確指出：“善于發現和提出問題，有解決問題的興趣和熱情；……，是‘實踐創新’素養的主要表現之一”．由此可見，激活學生的問題意識，事關創新思維、創新能力及核心素養．但是，學生的問題意識需要誰來激活？又該如何激活？本文以一道高考題的兩個教學判斷為例，在對比中尋求答案．不足之處，敬請同行批評指正．

2 教學實錄

2.1 高考真題

2008年江蘇高考數學第19題的第(1)小題：

設a1,a2,……,an是各項均不為零的等差數列(n≥4)，且公差d≠0，若將此數列刪去某一項得到的數列(按原來的順序)是等比數列：

2.2 教學背景

這是高一年級下學期學完《數列》一章的章節復習課，考慮到高一學生的學情，備課組內集體備課時刪去了原高考題的第(2)小題，僅選用了第(1)小題作為例題．關于如何講解這道例題，備課組內并沒有進行探討，兩位執教老師自由發揮，同題異構．

2.3 教學片段

片段1

教師用PPT出示2008年江蘇高考數學第19題的第(1)小題，在學生思考五分鐘之后開始提問．

師：生1，請分享一下你的思路．

生1：n=4時，即a1,a2,a3，a4成等比數列，接下來對刪去的項分類討論，一共有四種情況．若刪去a1或a4，剩下的三項既等差又等比，則d=0，矛盾；所以只能刪去a2或a3，接下來再分類討論．

師：好！你說我來板書．

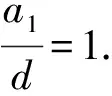
師：非常好！思路清晰，語言簡潔，結論也正確，但美中不足的是還不夠嚴謹．

師：對！這是最容易扣分的地方．第(2)題如何處理，也請一個同學來分享一下思路．

生2：項數大于等于6時，無論刪去該數列哪一項，剩下的項中總有三項是原等差數列中的連續三項，若成等比，則d=0，矛盾．下面考慮項數等于5的情形：

對于數列a1,a2,a3，a4,a5，若刪去a1,a2,a4,a5中的任意一項，得到的數列中總有三項既等差又等比，則d=0，矛盾.當刪去a3時，由a1,a2,a4,a5成等比數列，得a1(a1+4d)=(a1+d)(a1+3d)，解得d=0，矛盾. 綜上，n=4．

師：非常好！從兩位同學分享的解題過程來看，這道題的關鍵是分類討論，同時要注意“a，b，c等比”與“b2=ac”之間并不等價．另外，既等差又等比的數列是常數列，知道這個結論，對解這道題也非常有益．

片段2

師：請大家先看一道小題：

等差數列a,b,c，公差為d．若數列a,b,c也是等比數列，則d=．

眾生：0．

師：既等差又等比的數列是常數列，這個小結論看似不起眼，但在2008年江蘇高考第19題中卻發揮了大作用，大家有沒有興趣來做一番探究？ 教師用PPT出示探究1：

探究1如果一個等差數列項數為4，且公差d≠0，若將此數列刪去某一項，得到的數列(按原來的順序)能不能是等比數列？

在學生思考1分鐘后，教師開始提問．

生1：假設存在等差數列為a1,a2,a3,a4，且d≠0，下面對刪去的項進行分類討論：

若刪去a1，則a2,a3,a4是等比數列，故a1(a1+3d)=(a1+2d)2，公差d=0，與題設矛盾；同理，若刪去a4，公差d=0，與題設矛盾；故只能刪去a2或a3．

此時，數列為-4d，-3d，-2d，-d，滿足要求；

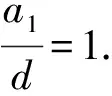
此時，數列為d，2d，3d，4d，滿足要求．

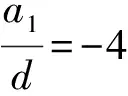
師：大家能提出類似于探究1的問題嗎？可以展開討論.

生2：還可以探究等差數列的項數為5的情況．

師：說說你的解題過程．

生2：假設存在數列a1,a2,a3,a4,a5滿足條件，若刪去a1,a2,a4,a5中的任意一項，得到的數列中總有三項既等差又等比，根據結論得d=0，與條件矛盾．若刪去a3，此時a1,a2,a4,a5是等比數列，則a1·a5=a2·a4，即a1(a1+4d)=(a1+d)(a1+3d)，解得d=0，與條件矛盾，所以不可能是等比數列．

師：還能提出類似的問題嗎？

生3：類似的問題多了，比如項數等于6，等于7，等等．

師：是嗎？

生3：哦，不對不對．項數超過5時，若刪去某一項后得到的數列(按原來的順序)是等比數列，則這個數列一定是常數列，所以對項數再進行探究沒有意義．

師：能根據這個發現編制一道填空題嗎？請大家思考．

生4：若一個等差數列項數為n(n≥5),如果刪去某一項后得到的數列(按原來的順序)是等比數列，則公差d=．(答案：0)

生5：若一個等差數列項數為n(n≥4)，且公差d≠0，若將此數列刪去某一項得到的數列(按原來的順序)是等比數列，則n的所有可能值為．(答案：4)

師：非常好！生5編的填空題其實就是高考題．(教師投影高考題，學生驚嘆不已)我們的探究結束了嗎？能不能再提出一些新的思考？

生6：把等差數列換成等比數列．

師：好主意！等差橫向類比等比，這是數列問題慣用的探究方式之一，大家不妨先從項數為4，且公比q≠1的等比數列入手．

教師巡視后投影學生的探究過程：

假設存在等比數列a1,a2,a3,a4，且q≠1. 若刪去a1，則a2,a3,a4是等差數列，故a1q+a1q3=2a1q2，公比q=1，與題設矛盾；同理，若刪去a4，公比q=1，與題設矛盾；故只能刪去a2或a3．

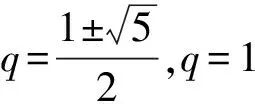
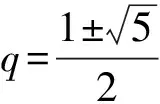
師：改變項數，有沒有類似等差數列的發現．

生7：項數n≥5時，若將此等比數列刪去某一項后得到的數列(按原來的順序)是等差數列，則公比q=1．

生8：若一個等比數列項數為n(n≥4)，且公比q≠1，若將此數列刪去某一項得到的數列(按原來的順序)是等差數列，則n的所有可能值為．(答案：4)

………

評注片段2中，整個教學過程總耗時近30分鐘.教師從一個學生熟知的小結論入手，起到先行組織者的作用；用“這個結論看似不起眼，但在高考題中能發揮大作用”這句話去吊足學生的胃口，激發學生的探究欲望，真是“小技巧，大智慧”．探究1是教師預先準備好的，它既承接了前面的小結論：等差又等比的數列是常數列，相當于對小結論進行了一個變式運用；又降低了題目的難度，符合高一學生的學情，實際上高考原題的表述，不少高三學生也感到抽象、有難度，高一學生更是如此；更為重要的是，探究1還是一個激活學生問題意識的“源代碼”，引發了學生對項數從4項到5項，再到n(n≥5)項的推廣，對數列類型由等差到等比的橫向類比．在學生這一連串的探究發現、自然生成之間，教師如同雙口相聲中的捧哏，穿針引線、遞火點鞭，適時、適度的激發學生的思維，把精彩留給學生，學生收獲的不僅是知識，伴隨著知識的生成，學生的問題意識、數學思維、數學能力及數學素養都得到了提升．同一道題目，不同的處理方法，前者耗時近15分鐘，后者耗時近30分鐘，也許，把片段2中學生提出的問題轉化成題目，片段1中的學生也許都能解決，但正如愛因斯坦所說的：“提出一個問題往往比解決一個問題更為重要，……”，從這個角度來說，這多花的將近一倍的時間非常值！

3 幾點思考

3.1 激活學生的問題意識，需要創設開放式的教學情境

開放式教學淵源于科恩(R．C．Cohn)1969年創建的以題目為中心的“課堂討論模型”和“開放課堂模型”——人本主義的教學理論模型；同時，還淵源于斯皮羅(Spiro)1992年創建的“隨機通達教學”和“情景性教學”——建構主義的教學模式．這些教學理論模型強調：學習是學習者主動建構的內部心理表征過程，教師的角色是思想的“催化劑”與“助產士”．開放式教學需要創設開放式的教學情境，開放式的教學情境包括開放式的現實情境、開放式的數學情境以及開放式的科學情境，但不管是什么類型的教學情境，都應該突出以提出問題、發現問題和解決問題為中心，注重學生自主探索與師生合作交流，重視數學聯系與知識建構，充分關注學生數學學習中的情感和態度[1]．創設開放式的教學情境，就是給學生的問題意識得到激活創造了最為合適的溫度和環境．

3.2 激活學生的問題意識，需要保護學生的好奇心

當前，高中階段單一的考試評價制度依然支配著教與學的價值取向，分數成為素質教育難以逾越的屏障，“快節奏、大容量”式的教學(不止是數學課堂)成為高效課堂的流行標簽，日臻成熟的“刷題”流水線在夯實數學基礎知識，提高解題技能的同時，也抹平了學生的棱角，扼殺了學生的好奇心和想象力．然而，好奇心是想象力的源泉，沒有好奇心，就沒有想象力．所以，日常教學中要改變過分依賴接受記憶、機械模仿等進行數學學習的方式；要給學生提供探究發現的機會，鼓勵學生

質疑提問，給學生提供表達自己的見解、思路和提出問題的機會；要善于發現學生的閃光點，及時給予肯定、鼓勵和表揚；在解題教學中，為激發學生的興趣和好奇心，激活學生的問題意識，對合適的內容要嘗試拆解和重組，以便于進行探究性學習，而不能僅僅停留在就題論題的層面上．創造力需要知識，但不僅僅是知識．“我沒有特殊的天賦，我只是極度的好奇”、“想象力比知識更重要”，愛因斯坦的兩句話無不發人深思．保護學生的好奇心，就是呵護學生問題意識萌芽和茁壯成長的種子．

3．3 激活學生的問題意識，需要提升教師的問題意識

隨著新課改的深入推進，“問題導向”的課堂教學模式受到一線教師的廣泛關注和普遍歡迎.“問題”是“導向”的媒介，好的問題不僅能精準制導，而且能提高學生的思維質量、激活學生的問題意識．好問題的來源不外乎兩類：一類是教材、教輔等資料上已有的，另一類是集師生智慧而生成的．現代教學觀下，學生的主體性需要得到充分關切，但班級授課制下教師依然是提出問題的主體．課堂觀察表明，因教師自身生成問題的意識淡薄而錯過了發問的最佳時機，因教師自身生成問題的能力不足而出現了不是問題的偽問題或者是缺少思維含量的低端問題，因教師壟斷發問的權限而導致學生的問題意識得不到激活和呵護，如此種種，學生一直扮演著被動解決問題的角色，學生的智力活動呈現出單一的、機械的特征．“給學生一杯水，教師要有一桶水，而且是活水”，教師提升自身的問題意識，就是給激活學生的問題意識引進的源頭活水．