指向核心素養的兩角差的余弦公式教學再設計

高長玉

(安徽省淮南市第二中學 232001)

“兩角差的余弦公式”(簡稱差余公式)是經典內容，涉及的數學知識廣泛，包含了豐富的數學思想與方法.本課的教學對學生獲得“四基”、提升“四能”、培養數學思維和發展數學學科核心素養都很有作用.本文在分析這一內容教學現狀的基礎上，以發展學生數學學科核心素養為指向，給出筆者的教學設計，敬請同行批評指正.

1 教學現狀分析

1.1 教材現狀

對比幾種不同版本教材，發現對本節知識引入與展開的處理方式有所不同：

(1)人教A版：先在章頭圖創設了一個涉及兩角和三角函數的實際應用問題情境，再在單位圓中推導α,β為銳角，且α>β時的兩角差余弦公式cos(α-β)，最后再借助向量工具證明α,β取任意角的一般情況.

(2)人教B版：直接提出“如何計算α+β，α-β的三角函數”，隨即給出公式.

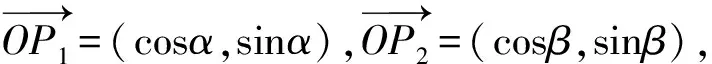
與北師大版教材處理方式類似，蘇教版和湘教版教材也采用向量數量積引導出差余公式.

1.2 課堂教學現狀

受教材編寫意圖引導、教師理念和學生能力差異等因素的影響，目前對本節知識引入與展開常見以下幾種方式.

(1)問題鋪墊、單刀直入式

按人教B版的方式，教師先是拋出諸如“如何求值sin75°,cos15°”的問題引出課題“兩角和與差的余弦公式”，再用向量法推導差余公式.

(2)情境設置、“猜想”指引式

教師設置類似于人教A版章頭圖中實際應用的問題情境，引入研究課題，繼而呈現諸如：

cos30°=cos(60°-30°)

cos90°=cos(120°-30°)

=cos120°cos30°+sin120°sin30°=0，

的結論，讓學生直觀感知，猜想公式，再引導學生用向量法給予證明.

(3)“巧設”問題、引導“探究”式

教師設置諸如“已知a=(cos75°,sin75°),b=(cos45°,sin45°),試求a·b的值”的問題，然后給出計算a·b的兩種方法：

解法一：a·b=cos75°cos45°+sin75°·sin45°；

解法二：a·b=a·bcos30°=cos30°，

再猜想公式，并用向量法證明.

對于上述知識引入、展開的方式，筆者認為有以下幾個值得商榷的問題：

第一，設置的問題有些突兀，不自然，不連貫，教師的主觀意志強；

第二，缺乏必要的引導，公式的發現成為“被發現”，導致學生思維的參與度不高.

第三，沒有顧及學生的認知準備現狀，在理解數學、理解學生、理解教學上都存在欠缺.

2 教學再設計

針對上述問題，并考慮到筆者所在學校是省級示范高中，生源狀況較好的實際，筆者對本課的教學進行了再設計，通過教學實踐檢驗，收到較好效果.下面呈現幾個片斷.

片斷一設置問題情境、引入新課

問題(1) 前面我們曾學習過許多三角函數誘導公式，你能寫出一些與大家分享嗎？

問題(2) 通過這些誘導公式你能提出一些新問題嗎？你有哪些初步的判斷？

對于問題(1)，要求學生寫的越多越好；通過問題(1)的分享，為問題(2)的思考做好鋪墊.

通過對三角函數誘導公式的舉例，引導學生對誘導公式進行觀察、比較、分析，初步判斷兩角和與差的正余弦函數sin(α±β),cos(α±β)與兩個角的正弦sinα,sinβ和余弦cosα,cosβ都有關系.

設計意圖①通過對誘導公式共性的歸納，給兩角和與差的三角函數公式提供猜想的指向，即兩角和與差的正、余弦與兩角的正、余弦皆有關系(但不是簡單的“分配律”的關系)；

②從誘導公式出發，在學生思維的“最近發展區”內提出問題，啟發學生從特殊到一般，思考兩角和與差的三角函數問題，有利于學生展開創造性思維，得出有關猜想.

片斷二猜想公式、知識展開

(1)研究對象的選擇

探究1： 兩角和的問題可以轉化為兩角的差嗎？反之呢？

探究2： 當α,β都是銳角且α>β時，α+β一定為銳角嗎？α-β呢？

學生在完成這兩個探究之后，自然選擇了先研究差角的余弦.

設計意圖①讓學生體驗化歸與轉化的數學思想方法，使其有一種金蟬脫殼的愜意；

②滲透從“特殊”入手的研究策略，幫助學生找到思維的切入點.

(2)探究特殊結論

學生聯想到同樣是“特殊情況”的三角函數誘導公式的推導方法，自然會想到：可以考慮在直角坐標系中，借助于單位圓，利用三角函數線探究銳角α-β的余弦函數.

筆者用問題串的形式引導學生作如下思考：

問題1：如圖1，在單位圓中，為了便于作出角α-β的余弦線，你認為設哪兩個角為α、β較為妥當？

圖1

圖2

設∠AOx=α，∠AOB=β，如圖2，過點B作BC⊥x軸(點C為垂足)，則cos(α-β)=OC.

由初步判斷，α-β的余弦與sinα,sinβ和cosα,cosβ都有關系.但對于角β，它的兩邊均不與x軸非負半軸重合，引導學生考慮構造含角β的直角三角形.

問題2： 怎樣構造含角β的直角三角形？你是如何想到的？

圖3

如圖3，學生一般會選擇過點B作BD⊥OA(點D為垂足),理由是“BD與BC方便建立聯系”.

問題3： 如圖3，在Rt△BOD中，已知什么，可知什么？

學生容易回答，已知∠AOB=β，OB=1,可知OD=cosβ，DB=sinβ.

問題4： 如何建立未知線段OC與已知線段OD、DB的聯系？

利用幾何畫板，分別用黃色、紅色閃現已知、未知線段，結合筆者在解題教學中經常提到的“四個什么”——已知什么，可知什么，要知什么，想知什么.學生會想到把這兩條已知線段投影到x軸上，可使未知與已知聯系起來.

圖4

如圖4，過點D作DE⊥OC(點E為垂足),則OC=OE+EC.

啟發學生，要求OE，就要觀察OE所在的三角形，學生容易得出OE=OD·cos∠BOD=cosβ·cosα.

如何求EC的長自然地成了一個呼之欲出的問題.

問題5： 在直角梯形ECBD中(如圖4)，可以知道哪些已知條件？

除了直角外，考慮到發現∠EDB=∠AOx=α有一定難度，可以借助多媒體將∠EDB與∠AOx的兩邊分別用綠色與紫色間隔性閃爍.

問題6： 在直角梯形中，求邊長問題，我們常用的方法是什么？

學生一般有兩種轉化方法：一種是過點B作BF⊥DE(點F為垂足)(如圖5);另一種方法是過點C作CF∥BD交DE于點F.都可以得出EC=sinβ·sinα(如圖6).

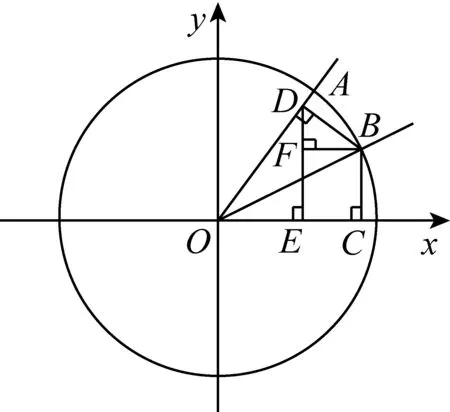
圖5

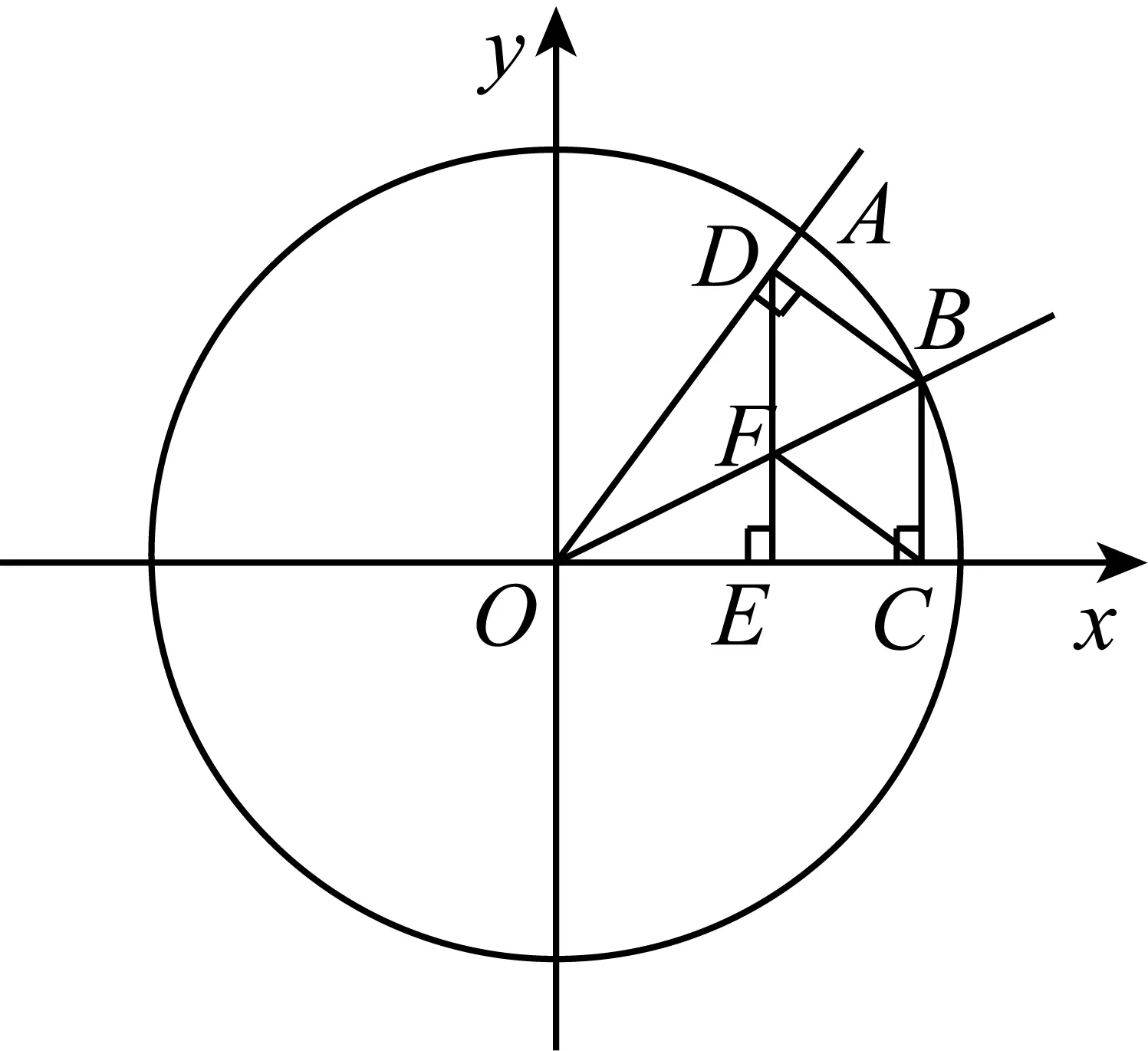
圖6

因此，有結論cos(α-β)=cosαcosβ+sinαsinβ.

設計意圖在學生的思維最近發展區內提問，通過層層遞進的問題引導學生思考與探究，給學生留下充分的悟的時間，使公式的發現一步步拾階而上.

問題7： 基于研究問題所采用的“從特殊到一般”的歸納策略，你會提出怎樣的猜想？

學生容易得出猜想：對任意角α,β,cos(α-β)=cosαcosβ+sinαsinβ成立.

追問：觀察表達式的右邊，從運算上看是什么形式？這與前面我們學過的哪一種運算在形式上類似？

學生容易想到平面向量的數量積運算.由于表達式右邊的結構是x1x2+y1y2的形式，學生想到構造向量(x1,y1)與(x2,y2)已是情理之中.

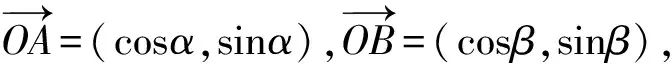
接著利用向量的數量積定義知猜想“正確”.

問題8： 你認為以上推導天衣無縫嗎？

在學生滿足于成功的喜悅之際，突然這么一問，很有戲劇性，容易引起學生的好奇心和求知欲.

在學生百思不得其解的情況下，教師適時點撥，請他們回憶一下向量夾角的范圍.他們很快會意識到以上只是證明了“α,β∈[0,π]，且α>β時，猜想成立”.

設計意圖滲透由特殊到一般的歸納策略，通過觀察、歸納、猜想培養學生的創造性思維能力；問題8的設計對培養學生的批判思維能力，對規范答題，解決“會而不對”、“對而不全”等問題很有幫助.

問題9： 針對以上角α與β的大小關系，你會作怎樣的分類？

當α=β時，結論顯然成立；

當α<β時，可以從兩個角度說明猜想成立：一是由誘導公式cos(α-β)=cos(β-α)，二是從余弦函數的奇偶性.

問題10： 現在已經證明了“α,β∈[0,π]時猜想成立”，怎樣擴大α,β的范圍？

學生意識到只要證明一個周期內猜想成立，再根據周期性便知任意角時猜想也成立，學生通過自主探究，可以有以下兩種處理方法：

方法一：設α∈(π,2π]，β∈[0,π]，令α=π+θ，

則左邊=cos(π+θ-β)=-cos(θ-β)，

而右邊=cos(π+θ)cosβ+sin(π+θ)sinβ

=-(cosθcosβ+sinθsinβ)，

又cos(θ-β)=cosθcosβ+sinθsinβ，從而結論成立.

考慮到對稱性，β∈(π,2π]時結論也成立.至此，證明了“α,β∈[0,2π]時，cos(α-β)=cosαcosβ+sinαsinβ”成立.

方法二：因為α,β∈[0,π]時猜想成立，

所以α,β∈[-π,0]時猜想成立(因為余弦函數為偶函數).

所以α,β∈[-π,π]時猜想成立.

設計意圖“從揭露已有知識在解決新問題時遇到的困難開始，以引起學生的好奇心和求知欲，調動學生探究新知的積極性”[1]在這一思想的指導下，培養學生分類討論、化歸與轉化的數學思想方法，讓學生進一步感悟由特殊到一般的歸納策略.

3 結束語

章建躍博士認為，“四個理解(理解數學、理解學生、理解技術、理解教學)”是教師專業化發展的必由之路，也是提高教學質量的根本保證.他同時強調，課堂教學要發揮數學的內在力量，在整個教學內容的展開過程中，都要發揮“一般觀念”的作用，加強“如何思考”、“如何發現”的啟發和引導.

在此思想的指導下，這節課本著一切數學課堂教學活動都從數學的本質出發，重視數學探究，關注學生發展.教學情境的設置既遵循數學知識的內在邏輯關系，又符合學生發展的需要，并輔之以信息技術手段，使得課堂教學科學而自然，“拉近”了教師、教材與學生之間的距離，學生身臨其境地經歷了數學知識的發生、發展的過程，切實地感悟到數學地認識問題、分析問題、解決問題的思想方法，對發展學生的“四基”、“四能”，理解數學知識的發生發展過程，進而提升數學素養等都具有非常積極的意義[2].