三維隨機裂隙介質建模與GPR響應計算

林景宜， 曾昭發， 李 靜， 張 領， 槐 楠， 胡志鵬

(1.吉林大學 國土資源部應用地球物理重點實驗室，長春 130026；2.吉林大學 地球探測科學與技術學院，長春 130026)

0 引言

土壤和巖石顆粒具有明顯的塑性、脹縮性、吸濕性和黏結性，是影響收縮特征的重要因素，巖土的收縮能力與土壤黏粒含量呈顯著正相關[1]，在遇水和失水后，會在上述性質差異較大的區域，產生有自相似性的裂隙分布，裂隙具有明顯的分維特征，且裂隙率、含水量、滲透系數和變形量之間具有一定的關系[2]；巖土中的裂隙帶是巖土中的軟弱結構和水的優先流動途徑[3]；坡體上裂隙的存在能夠導致優先流的發生，使地表水很快到達土壤深層，增大了入滲面積，提高了入滲速度[4]，同時，裂隙受雨水滲透力及滲透侵蝕的作用，不斷地延伸、擴大，最終形成滑坡[5]。可見對巖土介質中的裂隙帶進行探測，是災害預警和災害評價重要的基礎。

構成巖土的顆粒和孔隙大小不同，形狀各異，并且可能以各種方式連接，結構形狀十分復雜，通過常規的歐式幾何很難模擬巖土內部的結構。但是巖土結構狀況的一些參量，比如粒徑分布、裂隙發育程度、聯通狀況都表現出分形特征[6]，所以近年來，不少研究采用分形理論模擬巖土結構，Perfect等[7]、Perrier等[8]運用QSF分形理論對含聚合物顆粒的碎裂土壤結構進行了定量化模擬；Kravchenko等[9]、Medina等[10]計算出了土壤粒分形模型來模擬土壤結構和不同尺度下質量構成；Shepherd[11]用Koch曲線模擬孔隙通道連通狀況問題；Jiang等[12]建立基于混合型自相關函數的多尺度隨機介質模型來模擬介質的非均一性。然而，上述研究偏重于對巖土整體結構的建模，未能模擬出巖土中軟弱帶的局部特征。

巖土介質建模后，對模型進行數值模擬的方法眾多，其中探地雷達是對淺層介質探測的重要方法。探地雷達(GPR)數據的分析和解釋基于地下介質的電性參數，主要包括介電常數和電導率，應用在介質界面和目標形狀的探測方面[13]，在裂隙帶探測中也能發揮重要作用。Godio等[14]用探地雷達和其他方法綜合探測了含水層的裂隙帶和滲透層的幾何形態；鄧國文等[15]在隧道超前預測中用探地雷達對斷層破碎帶和裂隙帶進行了探測和解釋。在GPR數值模擬方面，Li等[16]采用CFS-RIPML邊界導出高階FDTD方法，應用到了GPR數值模擬中，有效降低了數值色散引起的誤差，提高了結果的準確性。在結果處理和解釋過程中，時頻分析方法起到了重要作用，Stockwell等[17]在以Morlet小波為基本小波的基礎上提出了可逆的S變換(ST)時頻分析方法，S變換采用高斯窗函數，繼承了短時傅立葉變換(STFT)和小波變換(WT)的優點，可以有效壓制噪聲，獲得更高分辨率的響應結果；鄧攻等[18]使用S變換對深反射地震弱信號進行了分解，提取出了被噪聲湮滅的低頻細節特征，提高了剖面的分辨率和同相軸的連續性。

筆者在前人研究的基礎上，使用三維Koch分形方法和Bruggeman等效介質理論，來模擬真實裂隙帶分布，并使用隨機等效介質理論建立巖土背景。建立一個三層背景下的裂隙帶模型，根據不同含水率計算裂隙的等效介電常數。對模型進行GPR數值模擬，定性研究其波場特征，再對響應進行S變換得到時頻特征，定量擬合含水率與響應的關系，最后進行裂隙帶深度的誤差分析。

1 建模方法

本模型的構建過程主要包括三維Koch曲線構造、裂隙帶形態控制、裂隙帶位置控制、裂隙成分等效、巖土背景隨機化幾個步驟。

1.1 三維Koch曲線構造

Koch曲線由瑞典數學家科赫(Koch)于1904年提出，是一種具有典型自相似性的折線，應用三維Koch曲線進行分形建模，可以更好地模擬出裂隙結構的自相似性和聯通狀況。

圖1 滿足廣義能量極小值原理的三維Koch曲線Fig.1 Three-dimensional Koch curve of the principle of generalized energy minimal value

三維Koch曲線如圖1所示，取一條線段P1P5，將其三等分，得到點P2、P4，設P1(xp1,yp1,zp1)、P5(xp5,yp5,zp5)，則由定比分點公式(1)可得P2(xp2,yp2,zp2)、P4(xp4,yp4,zp4)。

(1)

在三維空間中，ΔP2P3P4可以圍繞軸P2P4任意旋轉，所以點P3(xp3,yp3,zp3)不唯一。在自然界中非線性系統屬于強迫耗散動力系統，由廣義能量極小值原理和熱力學第一、第二定律可知，這種系統在經過足夠長的時間后，總是趨向一種不可逆過程最弱、系統廣義能量最小的有序狀態[19]。裂隙結構屬于不規則的非線性復雜系統，也遵循廣義的能量最小值原理。

設三維Koch曲線整體為一剛體系統，則其彈性勢能為“0”，系統總能量等于重力勢能，在系統質量一定時，重力勢能與系統重心位置有關，重心位置越低，則重力勢能越小，系統總能量也越小[19]。如圖1所示，當點P3(xp3,yp3,zp3)在Z方向上最小時，重心位置最低，此時ΔP2P3P4所在平面垂直于平面XOY，過點做一垂線L，由幾何關系知，L平行于平面XOY。以L為軸線，將線段P2P4順時針旋轉60，旋轉后點P4即為點P3所在位置。

(2)

(3)

M=+cosθ·(I-)+sinθ·A*

(4)

P′=P·MT

(5)

式(2)～式(5)中:A=[ax,ay,az]為單位長旋轉軸;θ為旋轉角;I為三階單位矩陣;P為待旋轉點的坐標;P′為旋轉后坐標。

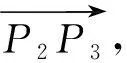
(6)

可求得旋轉后的坐標點P3，此時整個系統的總能量最小。將P1到P5的位置都求出后，每兩個相鄰的點之間再進行相同計算過程，重復幾層以后，可遞歸出一條滿足廣義能量最小值定理的Koch曲線。

1.2 裂隙帶形態控制

在遇水和失水后，會在收縮性質差異較大的區域，產生有眾多自相似性的裂隙分布，形成裂隙帶。

圖2 3維Koch分形裂隙的構造過程Fig.2 The construction process of 3D Koch fractal fissure

如圖2所示，設裂隙深度上、下限為htop和hbot后，將裂隙沿Z軸分n層，共n+1個界面，每層的底界面即為下一層的頂界面，每段裂隙的底端即為下一段裂隙的頂端。設裂隙帶在頂界面的中心點位置為Ptop_mid)(Xtop_mid,Ytop_mid,htop)，底界面中心點位置為Pbot_mid(Xbot_mid,Ybot_mid,hbot)，裂隙帶傾角為α，則由幾何關系可得：

tanα=

(7)

當Xtop_mid、Ytop_mid和α給定后，可求得一組Xbot_mid,Ybot_mid，確定了Ptop_mid和Pbot_mid的位置(圖2)。

(8)

式中:P1i_mid(x1i,y1i,z1i)為第i層裂隙帶的頂界面中心點坐標，P2i_mid(x2i,y2i,z2i)為第i層裂隙帶底界面中心點坐標。

設裂隙帶的長和寬為dx和dy，為了裂隙帶在內部體現出每條裂隙位置的隨機性，在(xni mid±dx/2,yni mid±dy/2)范圍內隨機取值，即可得到第i層裂隙的頂端點坐標(x1i,y1i,z1i)和底端點坐標(x2i,y2i,z2i)通過式(7)、式(8)可畫出第i層的分形裂隙，將各層連接即為一條裂隙，多次遞歸上部步驟即可畫出一個具有傾角的裂隙帶。

1.3 裂隙帶位置控制

經過處理后得到固定位置處的裂隙帶，還需將裂隙帶旋轉平移到指定位置。將裂隙帶各個轉折點位置記為一個矩陣[X,Y,Z]，X、Y、Z均為列向量，

(9)

(10)

式中:β為裂隙帶在xoy面上的旋轉角度;R為二維旋轉矩陣;[Dx,Dy]表示裂隙帶在x和y方向上平移;[Xnew,Ynew]為旋轉平移變換后的，在z方向上，裂隙帶位置沒有發生變化;Znew與Z相同。如圖3所示，先旋轉β改變裂隙帶傾斜方向，再平移D改變裂隙帶位置。可得裂隙帶的旋轉和平移后的位置[Xnew,Ynew,Znew]。

圖3 裂隙帶的旋轉平移過程Fig.3 The rotation process of the fissure belt

1.4 應用等效介質方法

經過上幾步處理，實際得到的是裂隙帶的轉折點骨架，還要給裂隙帶賦予實際的物理意義。將模型中的每一條裂隙看作是周圍眾多細小裂隙的等效，不僅能突出需要研究的尺度，還能提高計算效率，應用Bruggeman等效介質理論：

(11)

式中：εeff為Bruggeman等效介電常數；εi為第i類介質的介電常數，fi為第i類介質的體積分數，代入裂隙內空氣和裂隙周圍巖土的介電常數和體積分數，即可得到等效介電常數εeff，為了更好地體現出隨機效果，將εeff加上隨機變化δε(δε滿足高斯分布)：

εfra=εeff+δε

(12)

式中:εfra即為裂隙的等效介電常數，賦予介電常數后繪制成的裂隙帶(圖4),含有35條裂隙，分四層，傾角為45°,εfra=5。

圖4 Bruggeman等效處理后的裂隙帶Fig.4 Fissure belt after satisfying Bruggeman equivalent theory

1.5 裂隙帶巖土背景隨機化處理

將復雜非均勻介質中的非均勻體看成一個空間隨機過程，用統計學方法描述介質非均勻性所形成的非均勻分布就是隨機介質模型[13]。由于土壤顆粒的組成及排列方式復雜，還有水分、有機質和礦物質等原因的影響，所以隨機介質模型可以更準確地描述實際巖土背景的隨機非均勻性分布，即：隨機介質模型m(k)為均勻介質mi(k)和隨機擾動所δm(k)組成(δm(k)滿足高斯分布)，描述隨機介質模型的基本思路描述如下：

m(k)=mi(k)+δm(k)=mi(k)[1+f(k) ]

(13)

式中：三維空間位置矢量表示為k=(x,y,z)；用f(k)代表這種隨機介質的相對擾動的特征，其中f(k)=δm(k)/mi(k)。

對于f(k)的選擇，采用了小尺度非均勻性的橢球式混合型自相關函數：

(14)

式中：r是代表模糊度因子(當r=0時為高斯型橢圓自相關函數，當r=1時為指數型橢圓自相關函數，r介于兩者之間的，則為混合型自相關函數)；a、b、c分別代表x、y、z方向的自相關長度；再用式(15)作傅里葉變換，得到能量譜密度函數：

R′ (k)=‖F(k)‖2

(15)

式中:k=(kx,ky,Kkz)再加入隨機相位φ(k)，變換后得到功率譜函數：

(16)

對公式(16)中F′ (k)進行傅立葉逆變換，從波數域變換到空間域的R(x,y,z),得到隨機等效背景模型(圖 5),均勻介質mi(k)=5，x、y、z方向的自相關長度A=5、B=5、C=5,模糊度r=0.5。

圖5 隨機等效處理后的背景介質Fig.5 The medium after satisfying the stochastic equivalent media theory

2 模型實例正演

圖6所示為一個實例模型，模型大小為5 m×5 m×5 m，網格數為200×200×200，空間網格步長為0.025。模型背景分三層，第一層模擬表層土壤，厚2 m，介電常數平均值為10；第二層模擬濕潤粘土層，厚2 m，介電常數平均值為15；第三層模擬基巖，厚1 m，介電常數平均值為4。所有層面背景自相關長度A=5,B=5,C=5,模糊度r=0.5，背景電導率為0.01 s/m。第二層內的裂隙帶大小為5 m×1.25 m×2 m，傾角為38°，裂隙占裂隙帶體積的20%，背景介質占裂隙帶體積的80%。

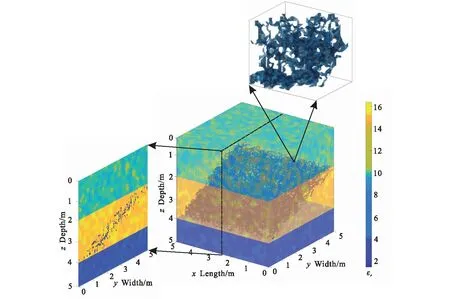
圖6 在隨機背景中的分形等效裂隙帶模型Fig.6 Fractal equivalent fracture belt model in random background

表1 不同含水率下裂隙帶的Bruggeman等效介電常數

從0%到20%取5種含水率，計算裂隙的Bruggeman等效介電常數，如表 1所示。將5種等效介電常數賦值給裂隙，并對其進行探地雷達正演模擬。

探地雷達(GPR)波脈沖激勵源的中心頻率為100 MHz，時間步長為0.05 ns，時窗長度為120 ns。正演模擬得到響應結果后去除直達波，如圖7所示，

圖7 不同含水率模型的探地雷達模擬響應結果Fig.7 Numerical simulation of GPR with different moisture content

左側圖7(a)～圖7(e)依次為0%、5%、10%、15%、20%含水率的探地雷達正演響應結果。在圖7(a)～圖7(e)中均可觀察到隨機背景造成的微弱擾動，除圖7(e)(含水率20%)外，分界面均較為清晰；在裂隙帶區域，由于內部介質比較復雜，電磁波傳播時的經歷多次反射和繞射過程，雙曲線波形較為散亂，同相軸更為模糊，但是仍能分辨出裂隙帶的位置和形狀；由于第二層介質介電常數為15，對比圖7(a)～圖7(e)可發現，含水率為10%時(圖7(c)，左)，介電常數與背景較為接近，裂隙帶造成的波形變化較小；裂隙帶與背景的介電常數相差越多，波形擾動就越大，尤其當含水率為20%時(圖7(e)，左)，也就是裂隙內充滿水的情況下，裂隙帶造成的混亂波形掩蓋了第二層分界面。

取2 m位置處單道記錄進行S變換，得到5種含水率響應的時頻圖，如圖7所示，右側圖7(a)～圖7(e)依次為0%、5%、10%、15%、20%含水率響應結果的S變換時頻圖。由于S變換壓制了噪聲，減弱了隨機背景的影響，使得兩層分界面和裂隙帶的異常均清晰可見。對比圖7中圖7(a)～圖7(e)，可以發現含水率為10%時(圖7(c)，右)，由于裂隙帶介電常數與背景較為接近，兩層分界面的異常明顯強于裂隙帶異常；含水率變低或變高，即介電常數與背景差異越大，裂隙帶異常就越明顯；且含水率較高時(圖7(d)和圖7(e)，右)，裂隙帶異常明顯強于分界面異常值。

不同含水率模型響應的2 m位置處單道記錄(圖7(f))也佐證了上述規律。在前50 ns，不同含水率模型響應基本一致；在含水率為10%時，裂隙帶位置(68 ns附近)振幅變化相對較小，而含水率越低或越高，振幅變化越大，異常越明顯。

由Bruggeman等效介質理論計算可得出介電常數與第二層背景相等(ε=15)時，含水率為8.63%，此時裂隙帶基本無響應。將不同含水率和其時頻圖中裂隙帶處的最大幅值進行三次多項式擬合處理，得到的擬合曲線和公式如圖8和公式17所示。通過時頻變換，我們得到了該模型下的裂隙帶含水率與正演響應的定量關系，根據此擬合公式，可用響應估算含水率。

圖8 不同含水率時頻圖在裂隙帶位置最大幅值的曲線擬合Fig.8 Curve fitting of the maximum amplitude of the time - frequency pattern with different water content

(17)

根據不同含水率時頻圖(圖7(a)～圖7(e)，右)中裂隙帶異常最大值位置的走時，可以計算出該道裂隙帶中心深度，誤差估計如表2所示，可以發現，響應結果對裂隙帶深度的估計較為準確。

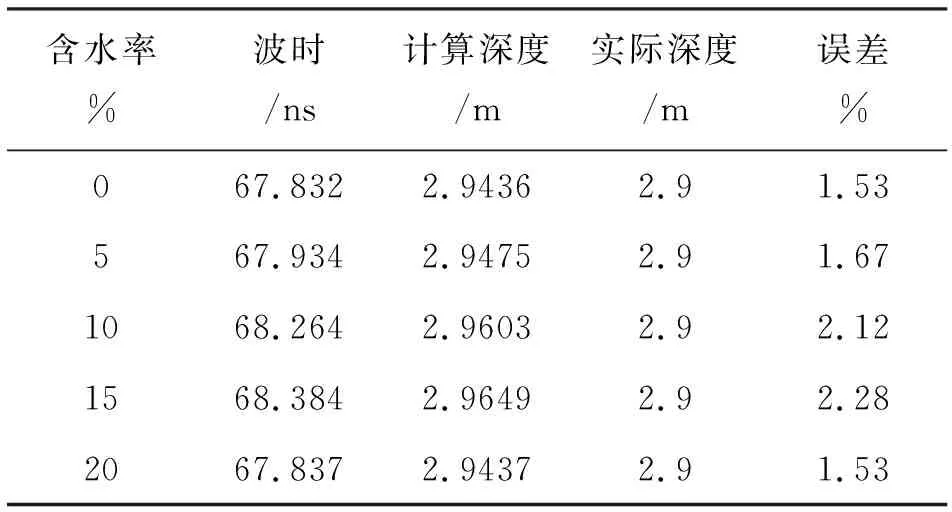
表2 不同含水率模型響應結果的裂隙帶深度誤差估計Tab. 2 The errors estimation of fissure belt for response results of different moisture model

3 結論

三維Koch分形曲線具有聯通性、隨機性和自相似性，通過Koch曲線模擬的骨架表現了裂隙分布的分維特征；對裂隙中空氣和水應用Bruggenman等效介質方法，得到多種含水率的巖土介電常數，滿足了不同情況和計算效率的需求；應用隨機等效介質方法使巖土背景呈現多尺度的隨機性，模擬了真實巖土介質的復雜狀況。

對不同含水率下的裂隙帶模型進行GPR數值模擬后，可以發現裂隙帶含水率對響應波形的影響較大。裂隙等效介電常數與背景相差越多，裂隙帶的響應越明顯，當裂隙內充滿水后，噪聲甚至可以掩蓋分界面波形。對響應進行S變換(ST)后分析其時頻特征，既壓制了混雜的噪聲，又可擬合出該模型下的含水率-響應曲線。根據此曲線的定量關系，可通過響應估算含水率。最后進行的裂隙帶深度的誤差分析,證實了數值模擬及時頻分析結果的可信性。此建模、探地雷達響應數值模擬及信號時頻分析方法可以為巖土體中軟弱帶及含水裂隙帶的探測提供參考。