基于智能突現的無人機群自主編隊控制研究

葉圣濤，方洋旺，朱圣怡

（空軍工程大學航空航天工程學院，西安 710038）

0 引言

無人機自20世紀20年代問世以來，其在戰爭中的地位日益提高[1]。多無人機協同自主編隊飛行是近年來的一個前沿領域，可充分利用單機資源，共同執行復雜任務。因此，針對無人機群自主編隊的深入研究具有重大意義。

群體智能（Swarm Intelligence）即群體產生的智能，與集體智慧類似[2]。突現計算（emergence computation，又稱涌現計算[3]）是多 agent系統（multi-agent system，MAS其中agent又稱個體或智能體）處理復雜問題時所展現出來的一種創新思路邏輯，是通過多個簡單模塊的相互溝通和協作來突現出更加復雜行為的計算系統。

在傳統的多無人機自主編隊中，需要無人機之間進行大量的信息交互，算法復雜，計算量大，耗費時間長，不能滿足系統的快速性、實時性要求[4]。王品、姚佩陽利用一致性算法求解了線性化無人機模型，并利用Lyapunov理論證明了系統的穩定性[5]。萬婧、艾劍良通過模糊控制為無人機編隊設計了控制系統[6]。本文提出了一種基于智能突現分布式控制策略來解決無人機群自主編隊控制的問題，為單個無人機設計簡單的運動規則，通過多個無人機的相互通信和影響來突現以形成編隊隊形[8]。

本文針對鳥群飛行機制中的Leader-Follower態勢進行建模：一方面利用有向圖描述無人機之間的通信協議；另一方面遵循聚類，防撞和速度一致三項規則[9]為無人機設計簡單的飛行控制器，通過多個無人機間的相互通信和協作以達到智能突現下的自主編隊。

1 無人機群自主編隊控制方法

1.1 基于Swarm模型的無人機編隊建模

考慮n維空間中具有個數分別為M個領航者，N個跟隨者組成的Swarm集合，用表示，其中為第i個領航者的位置，為第j個跟隨者的位置向量；為控制參數集；，為第i個領航者的速度向量，為第j個跟隨者的速度向量；，為第i個領航者的加速度向量，為第j個跟隨者的加速度向量。領航者和跟隨者的運動由以下方程控制：

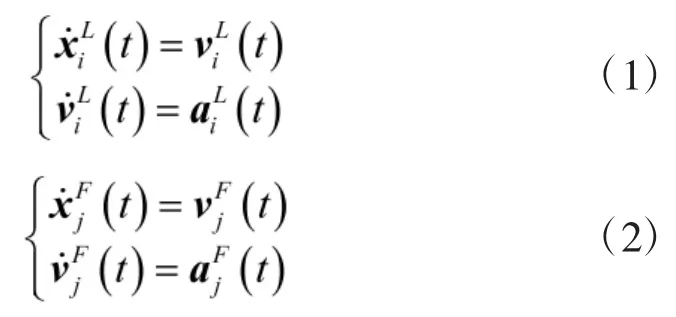
對于每一個領航者，其根據目標位置，采用比例導引法[10]命中目標。可得到位于水平面和垂直面的加速度和分別為

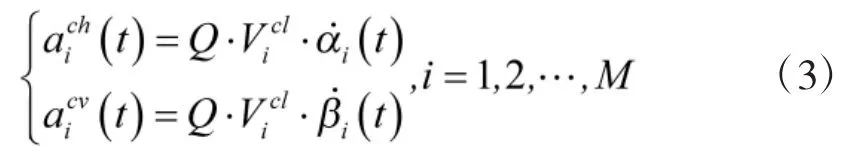
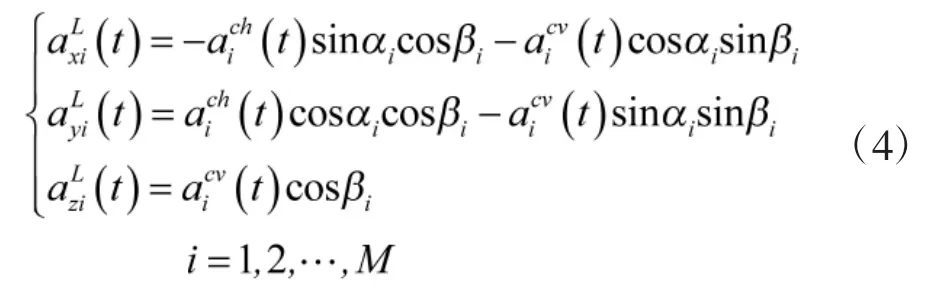
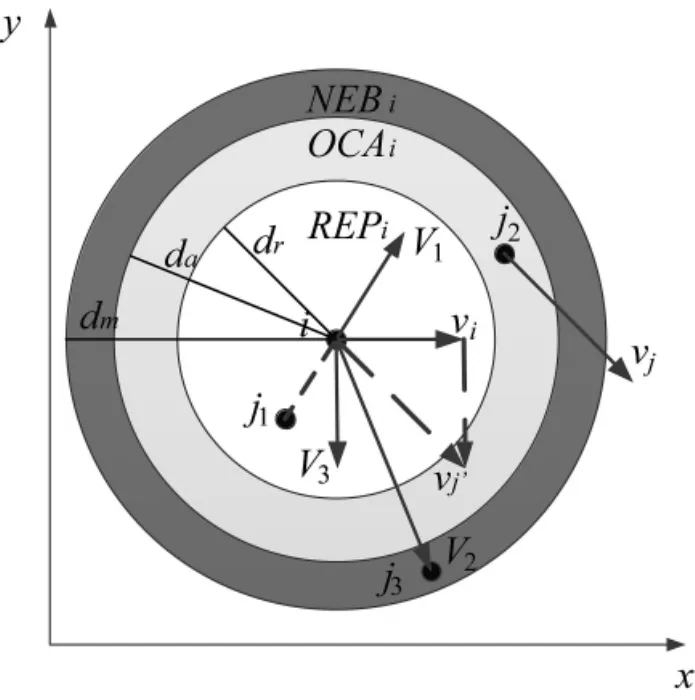
圖1 平面內無人機間影響作用圖

如圖1所示，定義第i個跟隨者的排斥域、吸引域和速度修正域[7]分別為

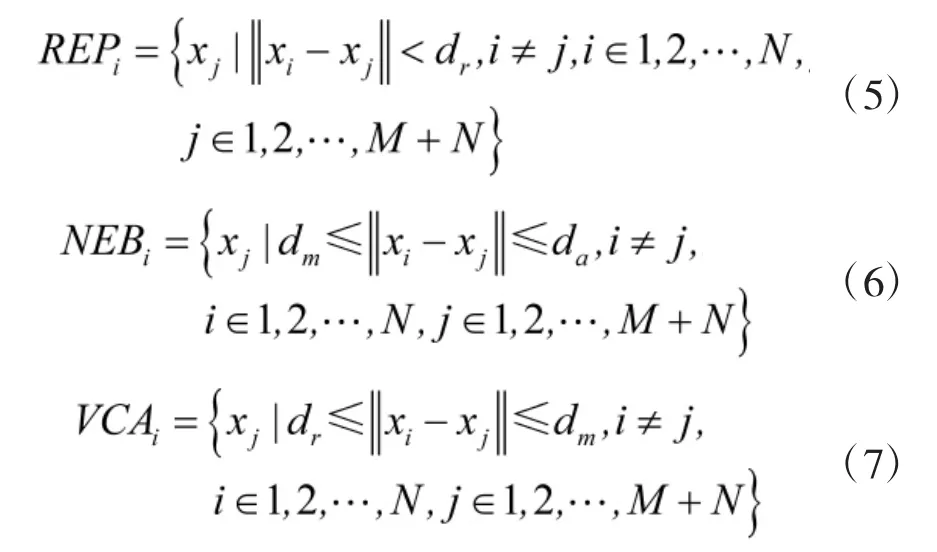
定義第i個跟隨者的排斥向量，吸引向量，速度修正向量[4]分別為：

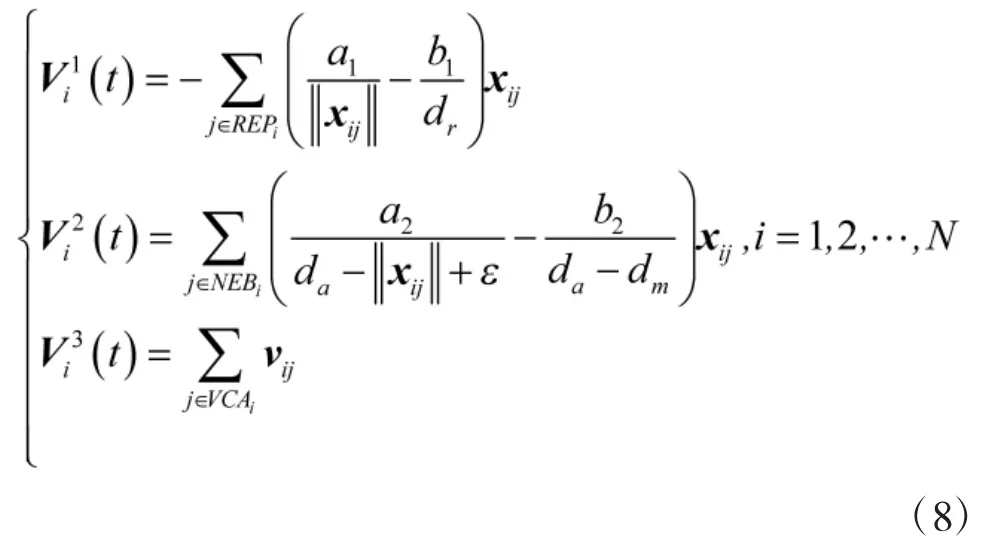
定義每個跟隨者的加速度為

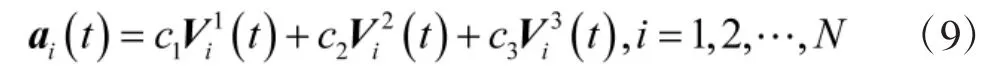
式中：ci（i=1，2，3）為增益系數，根據系統的規模和要求而調整。

假設每個無人機的加速度值及速度值由以下條件約束：

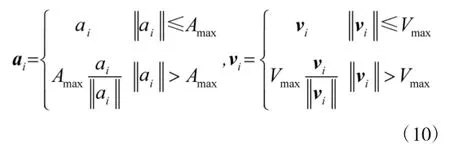
1.2 無人機運動建模

下面將建立三自由度的無人機運動學模型，由于每個無人機的模型（包括領航者和跟隨者）都是相同的，故去掉上下標。方程如下：

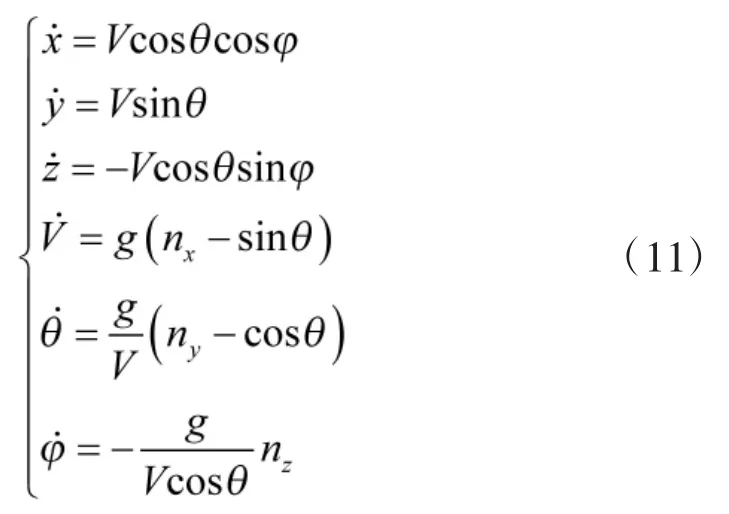
其中，（x，y，z）表示無人機在慣性坐標系中的位置；V，θ，φ分別表示無人機的速度、彈道傾角和彈道偏角；nx，ny和nz分別為無人機過載矢量在彈道坐標系各軸上的分量。

1.3 無人機制導控制方法

對于無人機群中的每一個領航者，假設其上安裝有高性能導引系統和定位系統，可以準確地發現目標，并且能夠實時測得目標位置及自身位置，從而測得自身到目標的視線角速度，進而通過比例導引律控制領航者的制導與飛行來攻擊目標。其制導與控制方法詳見參考文獻[10]。這里直接給出領航者的過載信息為：

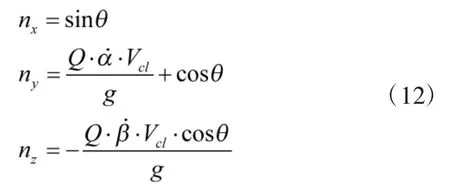
式中：Q為比例導引系數，一般取3到5之間；α，β分別為每一個領航者飛行過程中與各自目標的視線傾角和視線偏角；Vcl為每一個領航者與各自目標的相對接近速度。

為了簡化模型，這里取 nx=sinθ，使得式（11）中的，則Vj（t）為一定值，即每一個領航者以恒定速度飛向目標。

對于無人機群中的每一個跟隨者，假設無人機協同數據鏈能夠準確傳輸信息且無延遲，跟隨者能夠通過無人機協同數據鏈獲得周圍無人機的狀態信息。無人機間的通信方式用有向圖G=（V，E，A）表示無人機間的通信拓撲關系，如圖2。其中V={v1，v2，…，vn}為圖的節點集，每架無人機對應一個節點；E為圖的邊集，邊表示第i架無人機可以單向獲取第j架無人機的位置和速度信息；A=為有向圖的鄰接矩陣，當i=j時，aij=0，i≠j時，若 eij∈E，aij=1，否則 aij=0。

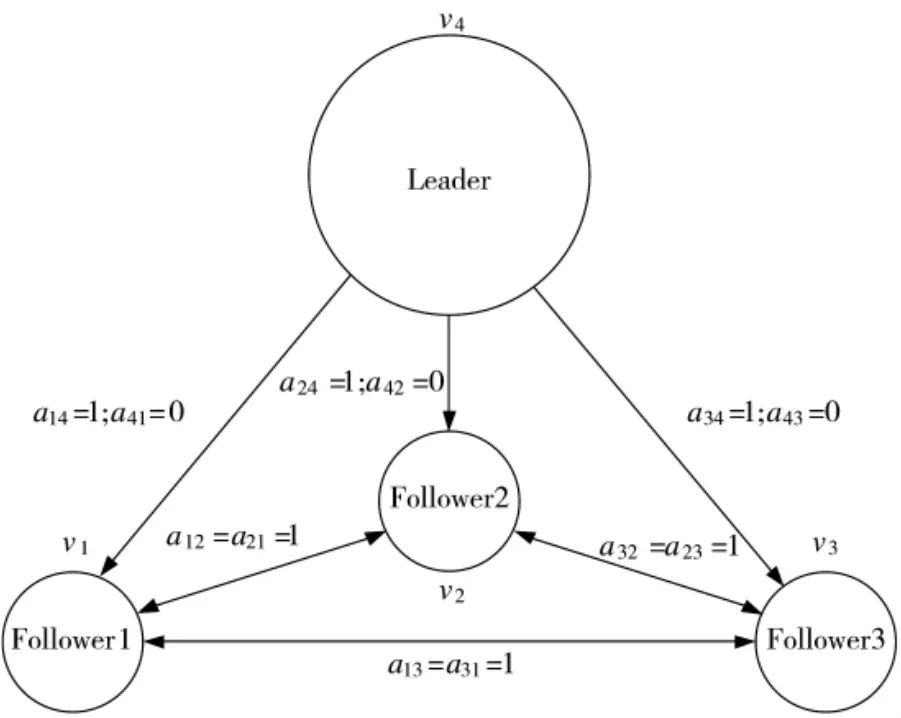
圖2 無人機群有向通信示意圖

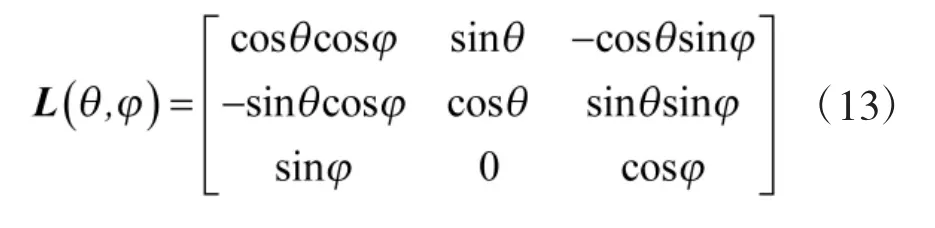
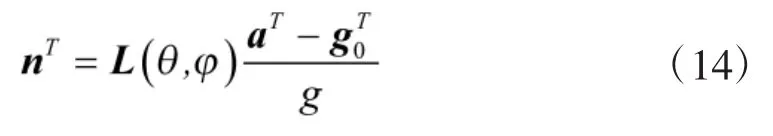
將得到過載矢量nT代入式（11），從而解得每一個跟隨無人機的位置信息。

2 仿真分析

考慮如下情景：在戰場空間中，存在敵方地面固定目標6個，我方由運輸機在高空均勻投放無人機若干架，其中包括具有高性能導引頭的領航無人機和普通跟隨無人機，仿真時間為40 s，步長為0.1 s。

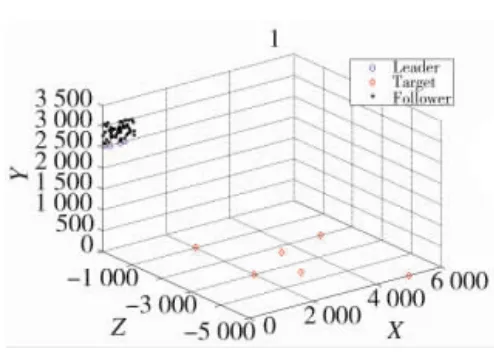
圖3 仿真初始時刻圖

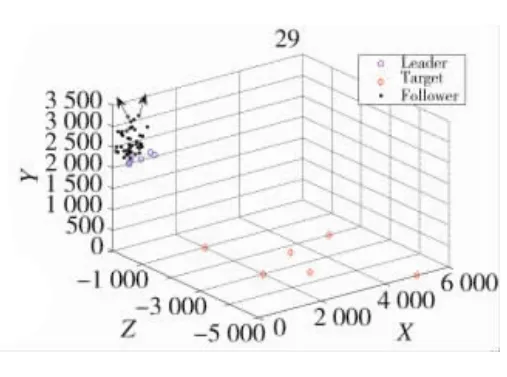
圖4 隊形散開避免碰撞圖

如圖3所示，仿真初始化，地面上有6個敵方固定目標，用紅色菱形表示，我方運輸機在高空隨機投放56架無人機，其中6架為帶有高性能導引頭及定位系統的領航無人機，其任務為探測敵方目標并實現制導，帶領著普通跟隨無人機攻擊目標，在仿真圖中以藍色圓圈表示；其余50架為普通跟隨無人機，其任務為跟蹤上領航無人機，保持集群飛行，毀傷地面目標，仿真圖中以黑色圓點表示。

如圖4，編隊初期，由于跟隨者和領航者之間的位置都是隨機，并且跟隨者之間的速度也不盡相同，無人機群整體呈現較混亂的態勢，如圖4所示的兩架跟隨無人機（黑色箭頭所指）由于初始位置距離整體中心太遠，速度方向向外，因此，有遠離整體中心移動的趨勢。其他跟隨無人機迅速通過數據鏈獲取通信范圍內其他無人機的速度和位置信息，由于初始投放距離短，使得無人機之間的距離都過于靠近，為了避免發生碰撞，無人機在受到排斥作用下開始有序散開，并開始逐漸編隊。

如圖5所示，一些在初始狀態下遠離整體的跟隨無人機，隨著距離的逐漸增大，吸引作用逐漸增強，排斥作用逐漸減弱，均有飛回無人機群整體的趨勢（圖5黑色箭頭所示）。

如圖6所示，隨著飛行的繼續，仍舊有跟隨者（圖6黑色箭頭所指）因為吸引作用不足而導致飛出了通信范圍，進而失去了無人機群的控制，從而運動呈現不規則性。

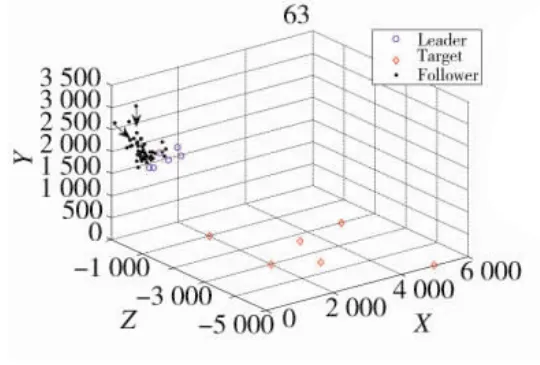
圖5 跟隨無人機飛回無人機群

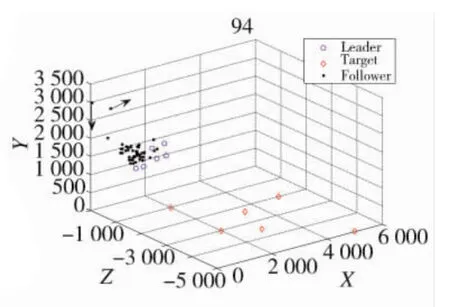
圖6 跟隨無人機飛出通信范圍失去控制

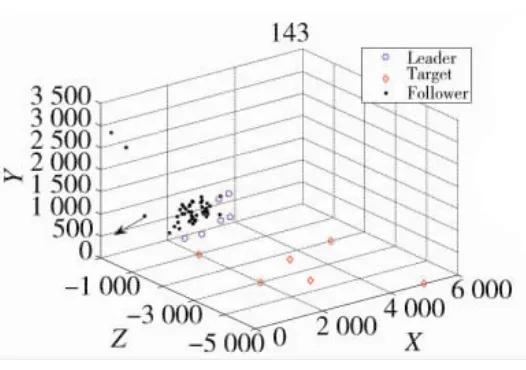
圖7 跟隨無人機飛出通信范圍失去控制

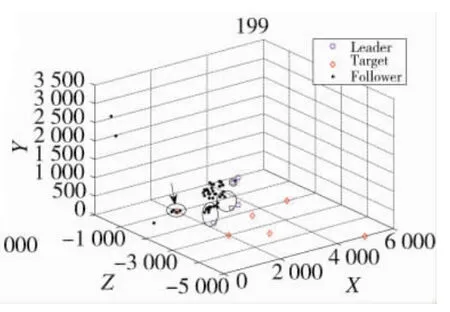
圖8 領航者1帶領跟隨無人機毀傷目標1

圖7中，在無人機群中，隨著各個領航者飛向各自的目標，跟隨者中突現出分群的現象，圖7中的無人機群已經開始逐漸形成Leader-Follower的初期態勢，由領航無人機帶領若干跟隨無人機飛向各自目標。不過仍然存在無人機（圖7黑色箭頭所指）飛出通信范圍而飛離無人機群的控制范圍。

圖8為仿真20 s左右，無人機群編隊飛行已經基本穩定，已經明顯出現Leader-Follower態勢。領航者1已經帶領4個跟隨者到達了目標附近，剩下的跟隨者繼續跟隨著剩下的領航者飛向目標，并且明顯形成編隊飛行（圖8黑色圓圈所示）。

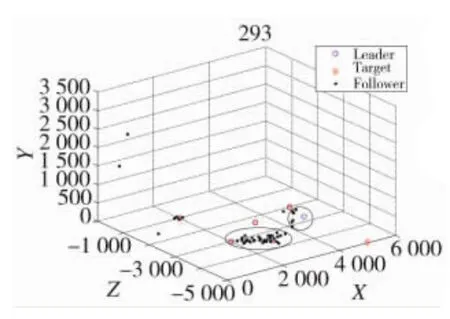
圖9 領航無人機2，4帶領跟隨無人機毀傷目標2，4

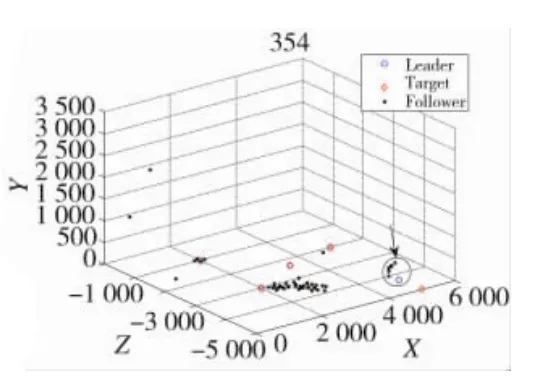
圖10 領航無人機6帶領跟隨無人機群飛向目標6

圖9中而由于目標2和目標4相對距離靠近，領航者2和領航者4共同帶領著一大群跟隨無人機（黑色橢圓圈所示）攻擊各自的目標。領航者5只帶領了一個跟隨無人機攻擊到目標5。

圖10中最終由第6個領航者帶領著剩下的跟隨無人機飛向目標（圖10黑色箭頭圓圈所指示）。

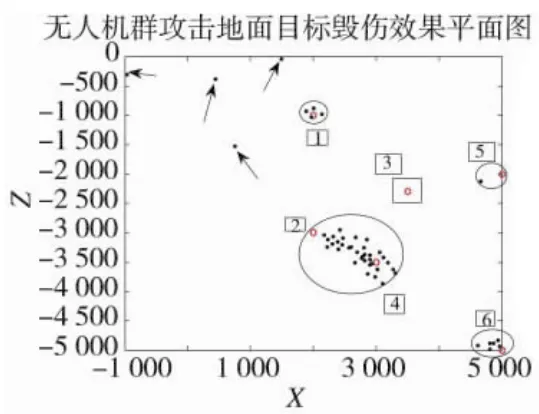
圖11 仿真結束時毀傷目標效果平面圖

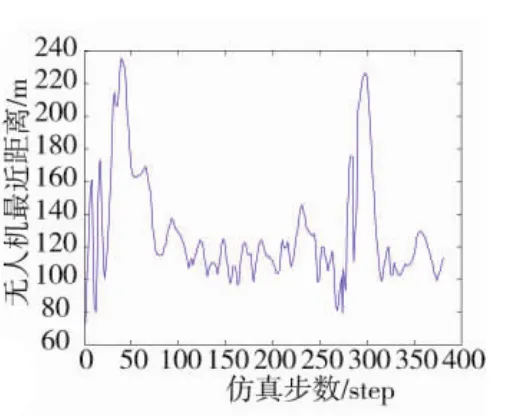
圖12 飛行過程中無人機間最近距離圖

下頁圖11為仿真結束時，所有個體在水平面的散落情況，可以清楚地看出，有4架跟隨者由于初始狀態或者飛出了通信范圍而不受控制（黑色箭頭所指），從而遠離了無人機群的整體，無序地散落在水平面內。剩下的跟隨者由6架領航者帶領分別飛向各自的目標，其中領航者2和領航者4由于目標位置相對接近，因此，共同帶領著一大批跟隨無人機攻擊目標2和4，領航者1、5和6都帶領著各自的跟隨者攻擊目標，領航者1和6所帶領的無人機群幾乎均勻地散布在目標周圍，毀傷效果優良；領航者5所帶領的跟隨者較少，毀傷效果一般。其中第3架領航者（黑色方框所圈）由于失去了對跟隨者的控制，沒有跟隨者跟隨，獨自攻擊目標。

圖12為無人機群飛行過程中，每一時刻無人機群中無人機之間距離最小值的變化曲線，由圖像可知，無人機之間的距離保持相對穩定，從而確保了無人機之間不會發生碰撞。

由上述仿真結果可以看出，利用本文提出的群體智能算法及分布式通信策略，當無人機飛行一段時間以后就產生突現現象，形成攻擊編隊對目標進行了有效攻擊，從而驗證了本文所提方法的有效性。

3 結論

本文對無人機群的自主編隊控制問題進行了研究，為了克服傳統無人機群編隊中交互信息量大，算法復雜的問題，提出了一種基于智能突現下的分布式無人機群編隊控制策略，能夠使無人機群中混亂的初始條件下[13]形成穩定的多Leader-Follower編隊形式，能夠準確地攻擊到指定目標并大大增加毀傷范圍，為未來戰爭提供一種新思路。本文研究的數據鏈之間的通信情況均為理想狀態，并未考慮延遲、丟包和噪聲的影響。在實際情況中，這些干擾都是不可避免的。因此，研究無人機群在存在各種干擾的分布式通信情況下的自主編隊控制問題對未來作戰具有重大意義，也是下一步的研究重點。