基于波導不變性的運動目標威脅分析

曾武 吳旭 周勝增

(上海船舶電子設備研究所，上海，201108)

現代海戰中，水面艦艇通常會面臨來自水下、空中的多種威脅。實時、準確的目標威脅分析，有利于指揮員分清主次、集中資源、重點應對威脅度大的目標[1]。目前常用的目標威脅分析方法主要有模糊邏輯法、神經網絡法、多屬性決策方法以及貝葉斯方法等[2]。這些方法大多需要引入專家知識構建規則或者推理網絡，從認知學角度上講，它們是根據已知戰場信息以及數據的融合處理，形成對目標威脅度評估過程的思維。貝葉斯網絡類似神經元網絡，能夠描述人類的推理過程，適用于復雜環境下目標的威脅度評估[3]。相對模糊邏輯而言，貝葉斯理論有嚴格的數學和統計學基礎，其推理模型具有通用性，可有效地將先驗和后驗信息統一起來，使得評估結果具有時間連續性和累計性，便于動態延伸[4]。

目標接近時間是評估威脅度的一個重要指標，接近時間越短，系統應對時間越不充分，目標的威脅度就越大[5]。大量試驗表明海洋波導中運動聲源的輻射聲場存在穩定的干涉結構，該現象可由波導不變量理論予以描述[6-9]。波導不變量是用于表征波導中聲源的距離和頻率間干涉結構的一個重要特征參量，干涉條紋中蘊涵了海洋信道和目標位置的信息。本文基于波導不變量理論，提取出目標的接近時間，利用被動聲吶對水下目標威脅分析提供重要參考。

1 波導不變性理論

海洋波導中，低頻信號遠距離傳播時，可用簡正波理論進行聲場分析。輻射點源深度為zs，信號頻率為ω，幅度為A(ω)，則距離點源水平距離為r,深度為zr的接收機接收信號的聲壓為：

由式（1）可知，聲強可以表示為：

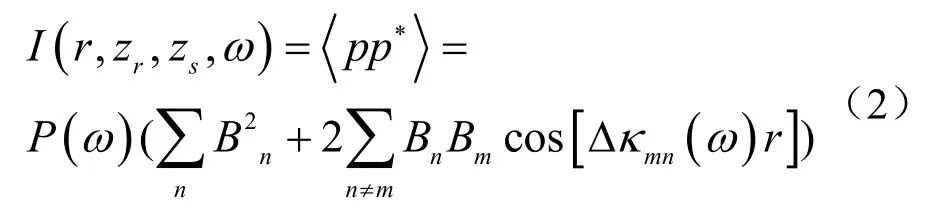
式中，P(ω)為功率譜，且假定其在處理頻段內連續且平坦，Δκmn為第m階與第n階簡正波水平波數差，即：Δκmn(ω)=κm(ω)-κn(ω)。由式（2）可知，聲強由兩部分組成：第一部分為直流分量，該項是距離r和頻率ω的緩變函數；第二項為震蕩分量，體現了不同階簡正波間的相互干涉，是聲強在r-ω平面上產生明暗相間干涉條紋的原因。對于r-ω平面上的干涉條紋，若Δr＜＜r0、Δω＜＜ω0（r0和ω0為中心距離和中心頻率），則可以認為干涉亮條紋上的聲強為常數，即I(ω,r,z)=const，則其全微分為0，即：

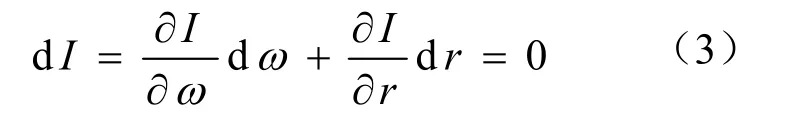
由式（2），有：

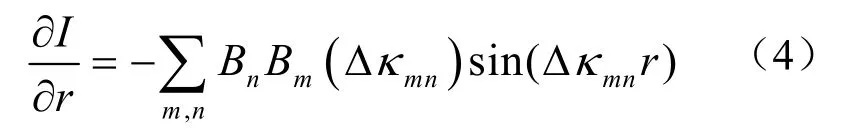
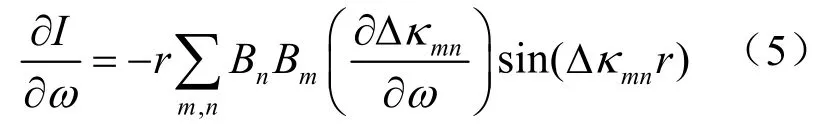
不影響結果前提下，式（4）和（5）中省略了隨距離與頻率緩變的常數。記第n階簡正波的相速度與群速度分別為vn、un，則由簡正波理論，有：

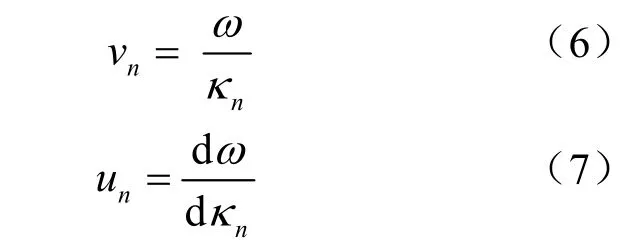
將式（6）、（7）分別代入式（4）、（5）中：

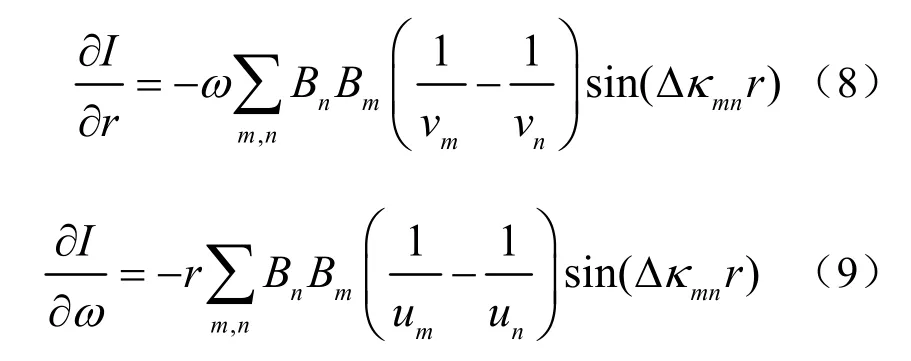
將式（8）、（9）代入式（3）可得：

定義第n階簡正波的相速度與群速度的倒數分別為相慢（phase slowness）與群慢（group slowness），分別記為。由式（6）和式（7）可知，二者間存在函數關系，以相慢為自變量，則有：

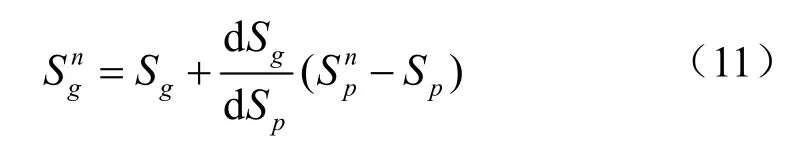
式中，Sp、Sg分別為這組簡正波的平均相慢與群慢。式（11）代入式（10），可知：

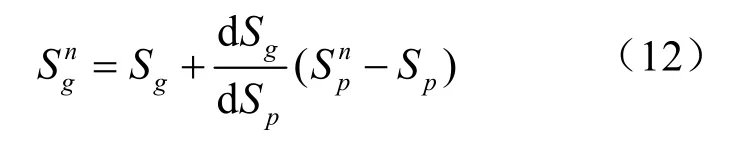
定義波導不變量β如下：

將式（13）代入式（12），可得：

式（14）表明，波導不變量可用于描述水下聲源輻射聲場的特性。

2 目標威脅分析處理

本文基于波導不變量理論提取目標接近時間，為被動聲吶的目標威脅分析提供參考。實際情形中，常得到的是聲強在頻率-時間平面的分布，記目標的徑向速度為v，則由式（14）可知：

文獻及試驗數據處理結果表明，多數淺海波導環境中，β值具備相當的穩健性，美國學者 Kuperman在淺海環境中所解算出的β值[8]表明，β值在1附近，較為穩定。

本文β默認為1.0。干涉條紋的斜率可通過圖像變換方法進行提取。dt/dw表示t-w平面上，LOFAR圖中干涉條紋的斜率，可利用Radon變換的方法求解，實際數據處理時，可利用滑動窗的方式進行實時求解。w為時頻窗中所處理干涉條紋當前的頻率值。本文為了提高提取特征的質量，對跟蹤目標LOFAR圖進行多頻帶劃分處理，求得多組接近時間值，設置合理門限進行篩選，進而通過中值濾波方法獲取高質量的目標特征。

3 試驗數據處理

在海上試驗中，某型水下目標由遠至近接近我方艦船。對同一態勢下的三組不同信噪比數據進行處理。圖1～3分別為信噪比0 dB、3 dB和6 dB時的經背景均衡處理后的跟蹤目標 LOFAR圖。對LOFAR圖進行多頻帶劃分，采用Radon變換獲取干涉條紋斜率，由式（15）求取目標接近時間，通過中值濾波方法獲取最終結果。

圖1 信噪比0 dB時的LOFAR圖

圖2 信噪比3 dB時的LOFAR圖

圖3 信噪比6 dB時的LOFAR圖

圖4為不同信噪比目標接近時間估計結果。由圖可知，波束輸出信噪比越高，所得結果越準確，當波束輸出信噪比達到3 dB以上時，估計誤差在15%之內。

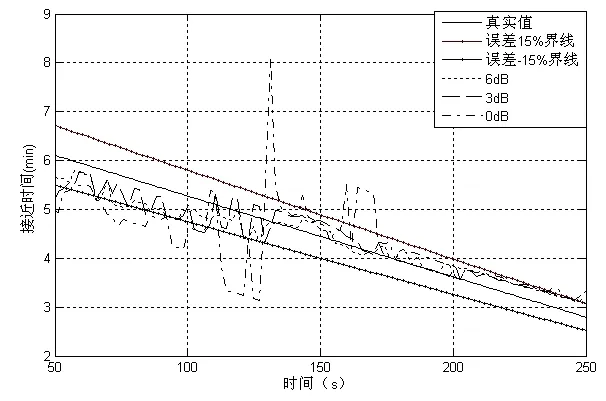
圖4 不同信噪比目標接近時間估計結果

4 結論

本文將聲場特性和目標威脅度分析進行融合，利用波導不變量理論求解目標接近時間。試驗結果表明，高信噪比情形下，基于該方法的估計結果精度較高，可為被動聲吶的目標威脅分析提供重要參考。