動態故障樹的邊值多值決策圖分析①

李 莉,劉翠杰,王 政,任逸飛

(北京電子科技學院 電子信息工程系,北京 100070)

1 引言

隨著信息時代的進步,科學技術尤其是電子技術、計算機技術的飛速發展,各種系統及設備的性能大大提高,其結構也變得越來越復雜,導致系統呈現出多種失效模式,給系統的可靠性分析帶來了新的問題.

故障樹分析方法 (Fault Tree Analysis,FTA)在六十年代初由美國貝爾研究所提出,并用于民兵導彈的控制系統設計,為預測導彈發射的隨機失效概率做出了貢獻.目前,FTA已廣泛應用于電子、電力、化工、機械、交通乃至土木建筑領域的關鍵系統定量或定性失效分析中.FTA通過分析系統潛在的薄弱環節,建立故障樹模型,為那些能夠導致系統失效的事件組合提供了數學和圖表的表達方法.但隨著容錯系統的大量應用,動態邏輯門的引入,傳統的基于最小割集(Minimal Cut Set,MCS)的故障樹可靠性理論和方法必須加以修正才能全面描述和反映動態故障樹的特性[1,2].越來越多的系統,例如計算機服務器系統、電信系統、水、氣以及配電系統等都要求有容錯功能,即在發生故障時,這些系統仍保持在可接受的或性能下降一級開展工作.近年來,人們逐漸將決策圖引入故障樹分析和復雜系統容錯功能的分析與設計中[3,4].

本文通過對邊值多值決策圖和其相關決策圖的介紹,以及邊值多值決策圖在動態故障樹分析中的應用,對邊值多值決策圖進行了全面深入的分析闡述.本文組織結構如下:第2節介紹了二叉決策圖、多比特函數二叉決策圖和多比特邊值二叉決策圖的基本知識并列舉了實例進行分析;第3節通過具體實例對多值函數、多值決策圖和邊值多值決策圖進行了介紹;第4節以網絡計算系統為例說明了邊值多值決策圖在動態故障樹分析中的應用,并分析了其性能;第5節對邊值多值決策圖進行了總結.

2 邊值二叉決策圖

2.1 二叉決策圖

二叉決策圖(Binary Decision Diagram,BDD)采用有向無環圖表示從{0,1}n到{0,1}映射的布爾函數f(x1,x2,···,xn)[5–9].

二叉決策圖可以根據香農展開定理,對布爾函數f(x1,x2,···,xn)中的變量逐次進行香農展開獲得:根節點表示布爾函數f(x1,x2,···,xn)自身,從根節點引出兩個分支,分別表示某個變量xi取0和1值時進行第一次香農展開后的布爾函數f(x1,···,xi-1,0,xi+1,···,xn)和f(x1,···,xi-1,1,xi+1,···,xn);布爾函數f(x1,···,xi-1,0,xi+1,···,xn)和f(x1,···,xi-1,1,xi+1,···,xn)可進一步進行香農展開,并將它們和各自的0-分量和1-分量連接;直至所有的變量均展開后得到最后的函數結果0或1,獲得布爾函數的二叉決策圖表示[5].也可以直觀的采用布爾函數的真值表獲得二叉決策圖.

例如:對于布爾函數f=(x1+x2)×x3

二叉決策圖(b)中0、1兩個終節點分別代表f的0和1兩個取值;xi下方的兩條分支分別表示xi取值為0的0-邊和xi取值為1的1-邊 .

二叉決策圖適用于具有兩個對立狀態的系統性能的判斷[10].例如圖1中的終點0和1分別表示系統無故障和有故障.

2.2 多比特函數二叉決策圖

多比特函數二叉決策圖是對二叉決策功能的擴展,多比特函數的每個變量由多位二進制數表示,而布爾函數的每個變量都是用一位二進制數來表示.下面對多比特函數的二叉決策圖進行舉例說明.

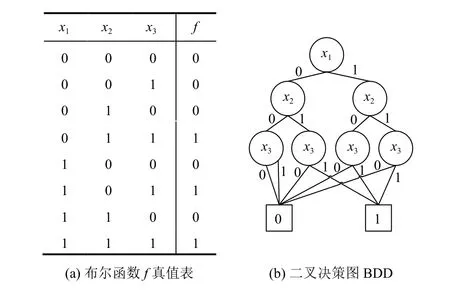
圖1 布爾函數f和f的二叉決策圖

表1(a)為sinX函數值表,假設我們選擇3 bit的二進制數來表示X和sinX,則取遞增單位為1/23=0.125,采用就近取整原則,可得二值化后的函數如表1(b)所示.

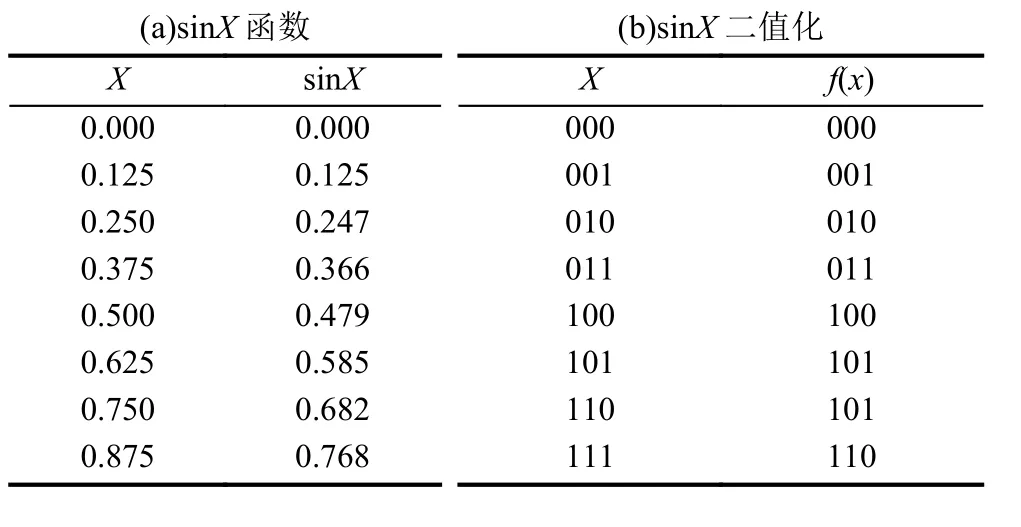
表1 sinX函數

表1(b)的二叉決策圖如圖2所示.節點X0、X1和X2分別表示變量X的3個bit位,X0是最低位,X2是最高位.虛線邊表示Xi的 0-邊,即Xi取值為 0;實線邊表示Xi的1-邊,即Xi取值為1.終節點表示函數的輸出結果.

多比特函數的輸出結果是由多位二進制數表示[11],即有多種輸出結果.多比特函數二叉決策圖適用于對多狀態且每個系統組件只有兩個狀態的系統進行表示.例如圖2中的7個終節點對應系統的7種不同運行狀態,而系統內各組件只有0和1兩個狀態,對應組件的有故障和無故障狀態.

2.3 多比特函數邊值二叉決策圖

邊值二叉決策圖(Edge-Value Binary Decision Diagram,EVBDD)是 BDD 的變體,表示整數值函數.EVBDD僅由一個表示0的終節點和具有整數權重邊的內部節點組成.EVBDD邊值求解規則如下:

(1)所有節點 0-邊總是具有零權重,即 0-邊的邊值為0.

(2)節點1-邊的邊值為當其子節點取值為0且其它節點取值相同,該節點取值為1時的函數值與取值為0時的函數值之差.即節點xi的1-邊的邊值e為:

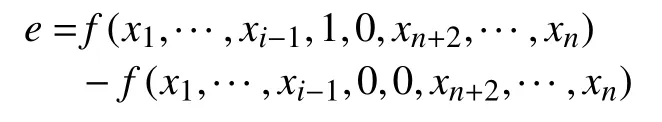
根據邊值求解規則,圖2的邊值二叉決策圖如圖3.

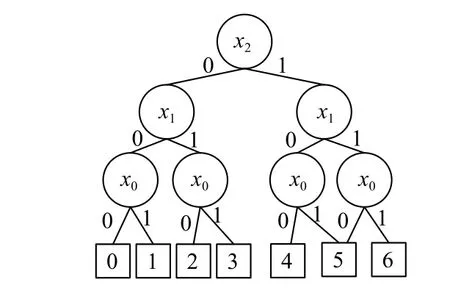
圖2 二叉決策圖BDD

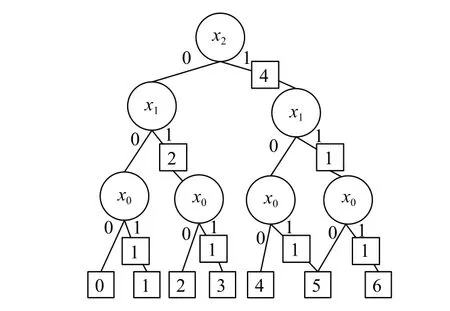
圖3 sinX的邊值二叉決策圖EVBDD

邊值相加即可得到函數的最終輸出結果.例如X21-邊的邊值,可以用X2X1X0=100時的輸出100減去X2X1X0=000 的輸出 000,結果等于 4,即X2的 1-邊的邊值為4.

為便于系統狀態的計算,可以對邊值二叉決策圖進行縮減,去掉冗余節點,簡化搜索路徑.冗余節點的定義如下:若邊值二叉決策圖的兩個或兩個以上同名節點的0-邊或1-邊均指向相同的分支子節點,或均指向終節點,且1-邊的邊值相同,則此同名節點存在冗余.縮減規則:

(1)對邊值二叉決策圖由下至上進行遞歸判斷,判斷是否存在冗余節點;

(2)對存在冗余的同名節點,保留一個節點即可,直至邊值二叉決策圖中不再存有冗余節點.

縮減后的二叉決策圖的函數輸出結果由邊值的和計算獲得,所以終節點由0來表示[11].圖3的縮減邊值二叉決策圖如圖4所示.圖3中四個X0的1-邊的邊值完全相同,且均指向終節點,所以可以刪除其它三個X0節點.

多比特函數邊值二叉決策圖的應用類似于多比特二叉決策圖,區別在于系統最終狀態由邊值的和來表示.

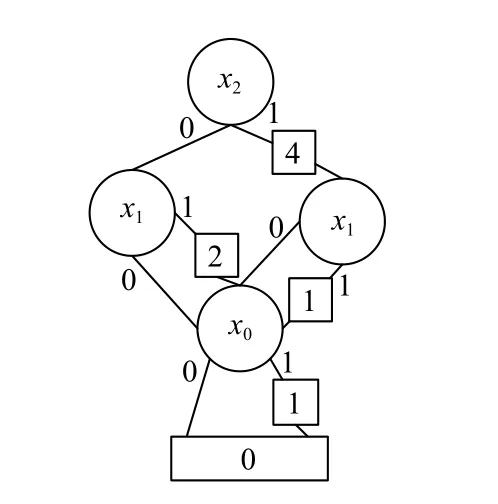
圖4 縮減后的邊值二叉決策圖EVBDD

3 邊值多值決策圖

3.1 多值決策圖

如前所述,當系統的狀態多于2個時,我們稱系統為多態系統.若系統中的各個組件也具有多個狀態時,我們稱系統為具有多狀態組件的多態系統,簡稱為多態系統.文獻[3]指出多態系統的性能、容量或系統的狀態可靠性級別都可以用系統的狀態來表示.

多態系統的狀態僅僅依賴系統組件的狀態.含有n個組件的系統可以被認為是一個多值函數f(x1,x2,···,xn)的映射:R1×R2×···×Rn→M,其中每一個xi代表Ri狀態的一個元組,Ri={0,1,···,ri-1}是組件的狀態集,M={0,1,···,m-1}表示系統的狀態集.此時多值函數被稱為多態系統的結構函數.在許多應用中,一個系統的狀態及其組件是完全有序的,并且該系統組件的運行狀態會影響整個系統的運行狀態.因此,通過以升序的方式將值分配給每個狀態,結構函數通常會變成單調遞增函數.即多值函數f(x1,x2,···,xn)當且僅當對于任意的xi是單調遞增函數,即,

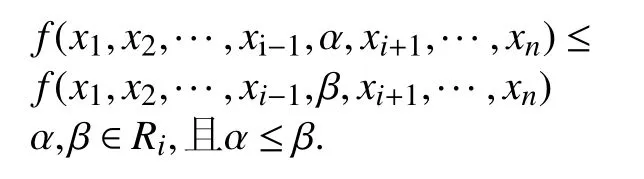
可以定義當xi取值為0時,為組件的最壞狀態即組件完全故障,當xi取值為ri–1時,為組件的最佳狀態即組件完全無故障;當f的值為0時,為系統的最壞狀態即系統完全故障,當f的值為m–1時,為系統的最佳狀態即系統完全無故障.隨著組件狀態值的增加,系統的狀態值也增加,即組件的故障越少,系統的故障就越少,運行狀態就越好.

多值決策圖(Multiple-valued Decision Diagrams,MDD)是反映部件狀態與系統狀態之間關系的有向無環圖.MDD的獲得與BDD的獲得類似,通過香農展開定理,重復應用于多值函數的各個組件獲得.MDD的內部節點表示通過向某些組件賦值從而獲得的f的子函數,每個內部節點具有對應于組件值的多個輸出邊[3].例如對于多值函數

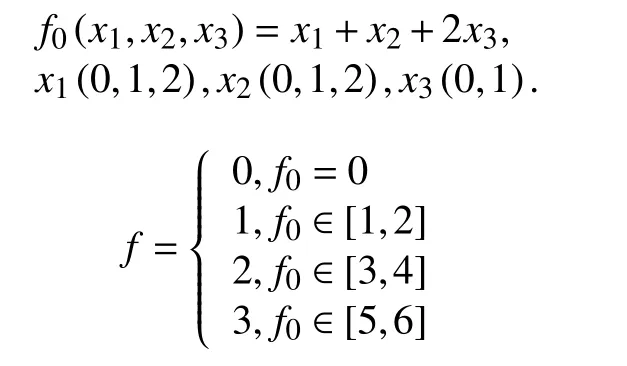
由以上的多值函數f得到的取值表如表2所示,圖5為其決策圖,圖中的終節點 0,1,2,3 分別表示多值函數f的取值.

表2 多值函數f的取值表

3.2 邊值多值決策圖

邊值多值決策圖(Edge-Value Multiple-valued Decision Diagram,EVMDD)是多值決策圖的擴展,它包括表示0的一個終節點和具有整數權重邊值的內部節點;0-邊總是具有零權重.在 EVMDD 中,函數值被表示為從根節點遍歷到終節點的邊值的和[3,12,13].

以圖5為例,使用與邊值二叉決策圖相同的邊值求解和縮減規則得到的多值函數f的邊值多值決策圖如圖6所示.因為x2的分支子節點x31-邊的邊值完全相同,所以可以合并.x1的0-邊的分支子節點x2和2-邊的分支子節點x2的邊值相同,所以進行合并.x1的1-邊分支子節點x2與其它邊的分支子節點x2的邊值不相同,所以不能縮減.

經過比較,發現MDD有7個節點,而EVMDD只有4個節點,減少了3/7.文獻[3]中提到計算的時間復雜度與決策圖中的節點數量成正比,所以在計算的時間復雜度方面,EVMDD比MDD更有優勢.

圖5 多值函數f的 MDD

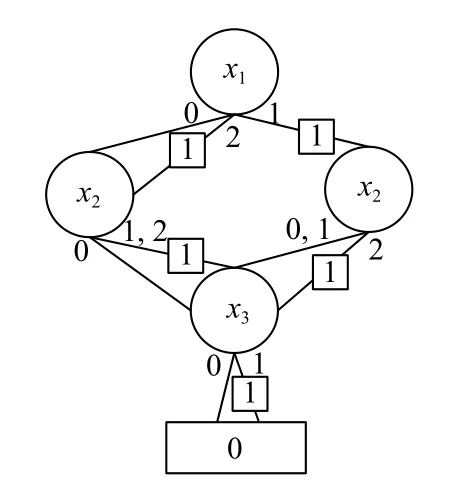
圖6 多值函數f的 EVMDD

4 案例研究

4.1 高度可靠的網絡計算系統

以文獻[14]中提到的高度可靠的網絡計算系統為例,系統架構如圖7所示,通過兩個不同的數據進程提供網絡計算服務.系統分為兩個部分,Complex A 和Complex B.每個子系統包含一個服務器(SVR)、一個存儲子系統(STO)及一個網絡子系統(NET).存儲子系統采用鏡像存儲方式,包含一個存儲控制器及兩個存儲空間.當存儲控制器故障時,該存儲控制器故障.備用服務器SVR_C作為失效備援,SVR_C和兩個服務器SVR_A、SVR_B間采用心跳連接.根據該系統的動態故障樹DFT模型可以得到文獻[10]中的系統性能初始MDD,如圖8所示.

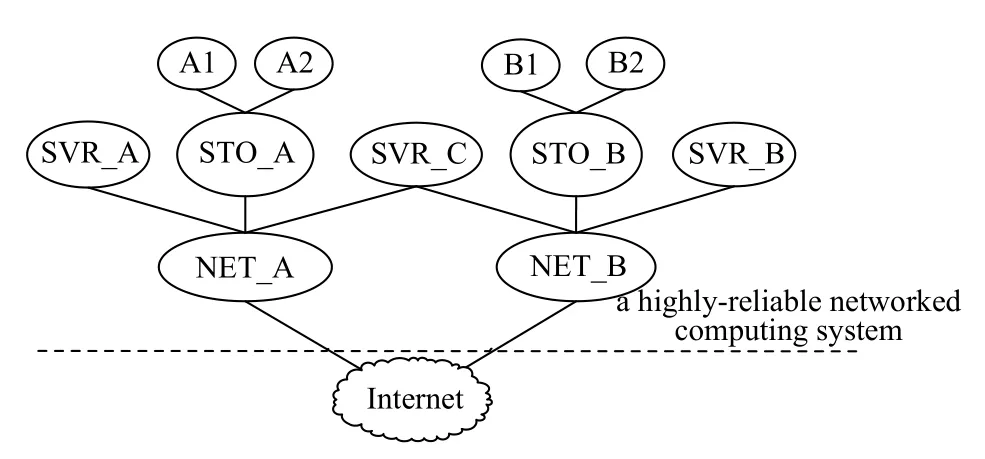
圖7 高可靠性網絡計算系統

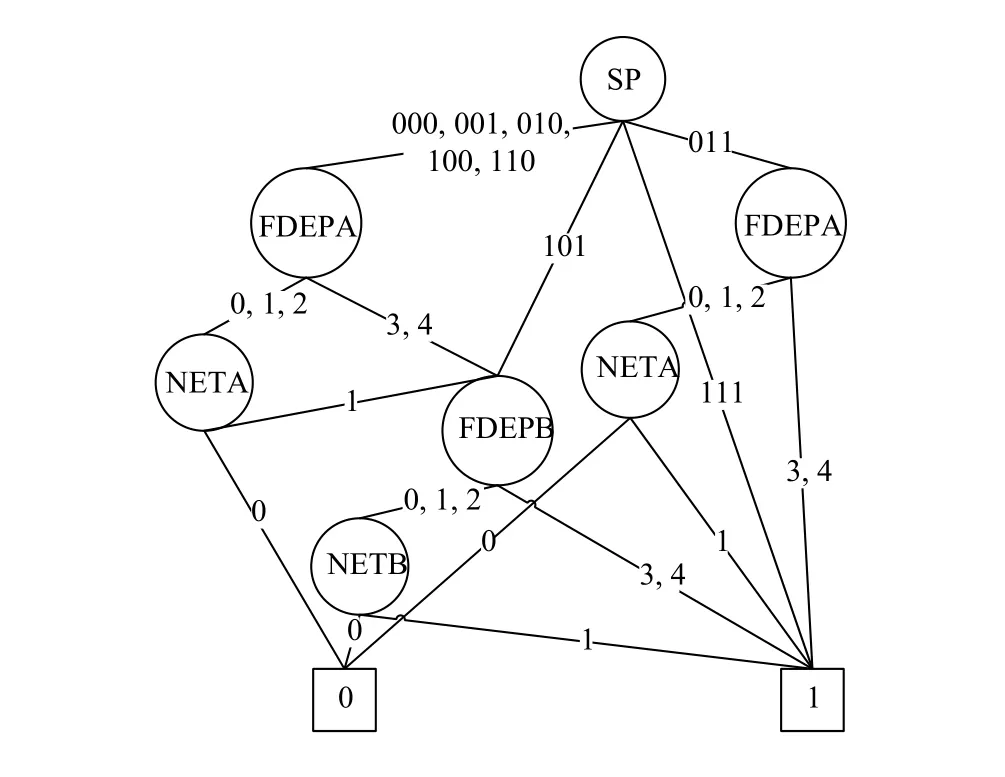
圖8 高可靠性網絡計算系統的初始MDD

下面用文中給出的邊值多值決策圖的構造方法來獲得其EVMDD.將SP的4個分支分別用0到3的4個狀態值代替.即000,001,010,100,110用狀態0代替;101用狀態1代替;111用狀態2代替;011用狀態3代替.

圖9所示的系統動態門的MDD,按照本文所述的邊值求解規則和縮減規則得到圖10所示的EVBDD.

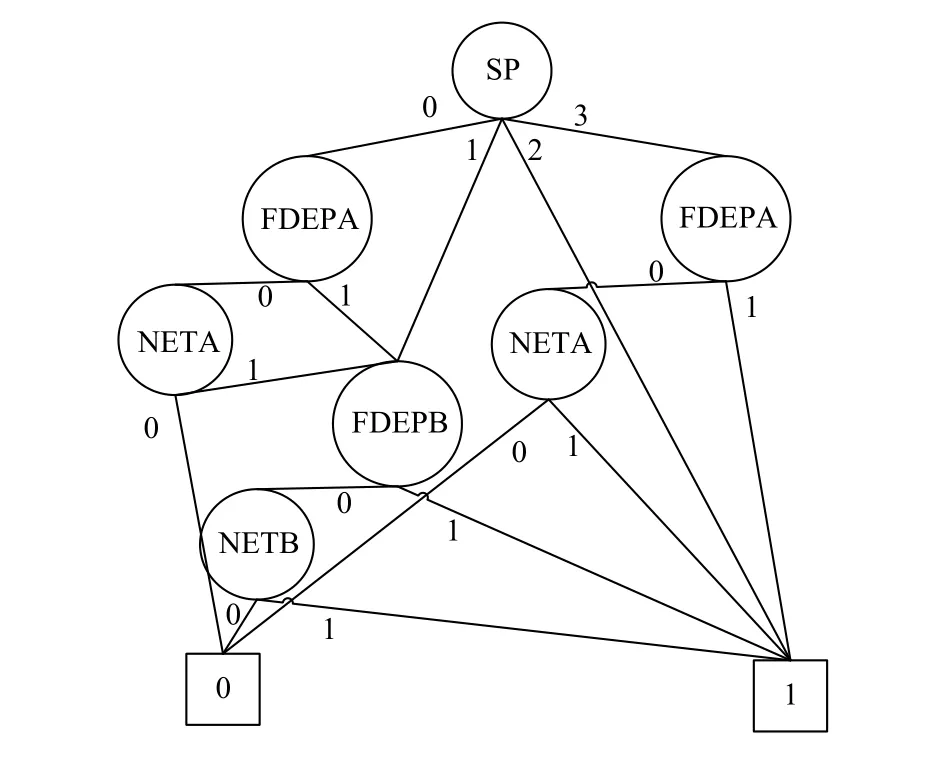
圖9 高可靠性網絡計算系統動態門的MDD

由于此系統比較簡單,所以EVMDD在節點和分支的數量上減少的優勢沒有顯現.但依據圖6可見,相對于MDD來說,EVMDD在節點和分支的數量上都有所減少,系統越復雜,邊值多值決策圖在節點數量上的優勢越明顯.

4.2 環境檢測物聯網絡

我國空氣污染形勢嚴峻,部分城市面臨霧霾、沙塵暴等環境問題.環保部門積極開展大氣污染治理,其核心是對污染源的精準監測和對污染數據的精準分析.隨著物聯網技術的發展,多功能、智能化、小型化的微觀站監測設備得到廣泛使用.研究環境檢測物聯網絡故障樹的邊值多值決策圖模型,假設環境參數主要有溫度、濕度和氣體濃度,分別用X2、X1、X0來表示,設備的最終檢測狀態用f來表示,每一個參數的測量都有一個備份電路.因此用狀態0表示完全無故障,狀態1表示部分故障,狀態2表示完全故障.得到多值函數f的取值表如表3所示,環境監測物聯網絡MDD如圖11所示.

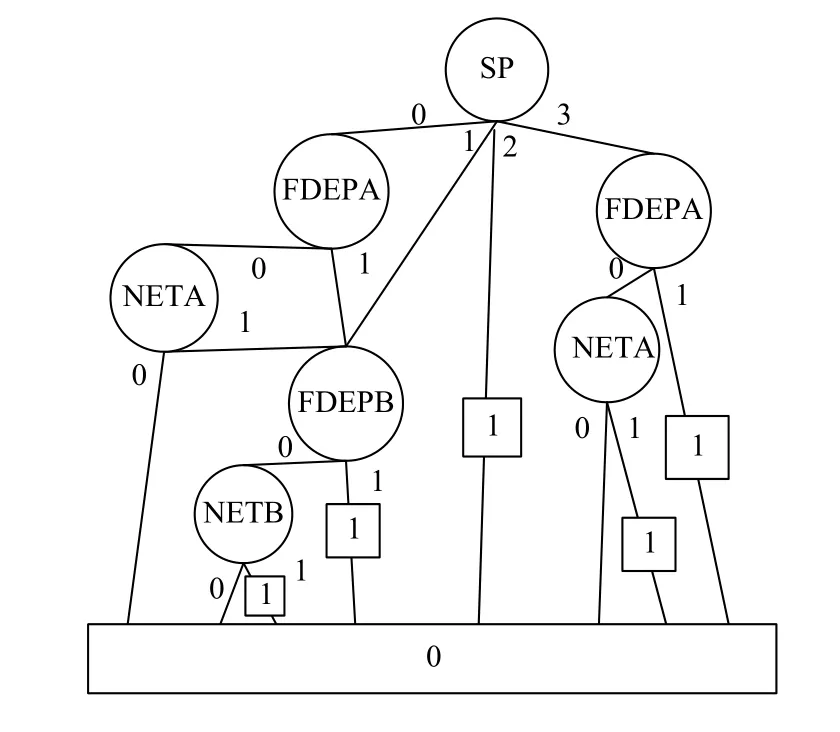
圖10 高可靠性網絡計算系統動態門的EVMDD

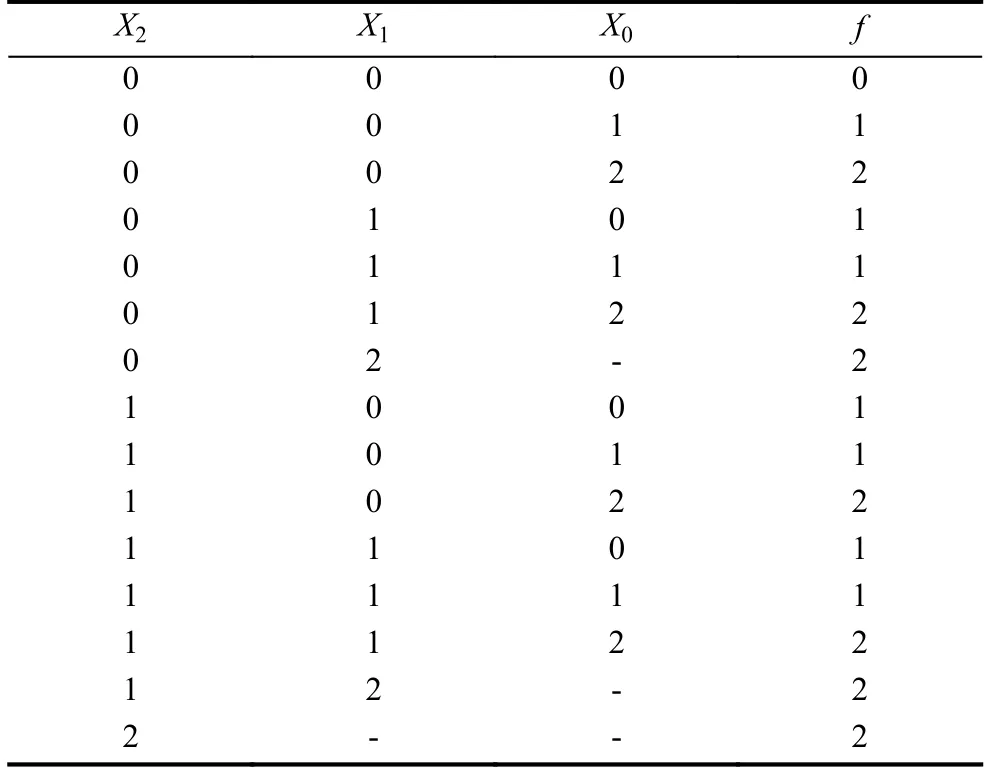
表3 多值函數f的取值表

按照本文所述的邊值求解規則和縮減規則得到如圖12所示的環境檢測物聯網絡的EVMDD.

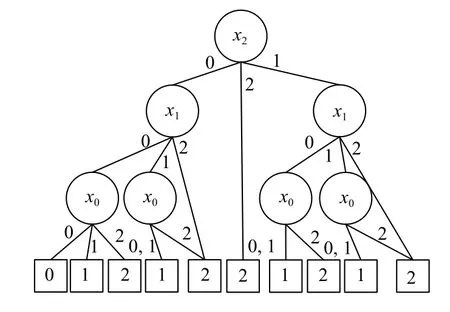
圖11 環境檢測物聯網絡的 MDD

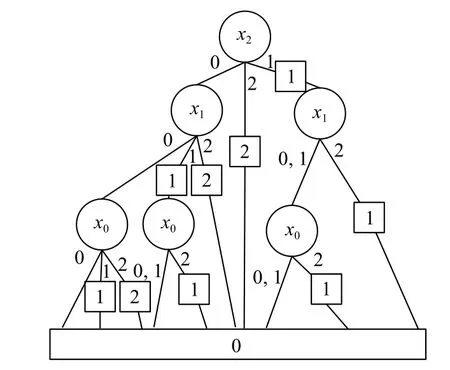
圖12 環境檢測物聯網絡的 EVMDD

通過對環境檢測物聯網絡的MDD和EVMDD的比較,用EVMDD用更少的節點來表示環境檢測物聯網絡.而計算的時間復雜度與決策圖中的節點數量成正比,即節點數越少時間復雜度越低,因此EVMDD在系統的故障樹分析方面更有優勢.特別地,隨著狀態數的變大,EVMDD的節點數遠小于MDD的節點數.我們預計系統將在未來變得更加復雜,并且狀態數將變得更大,因此,EVMDD比MDD更有發展前景[15,16].

5 結束語

本文對邊值二叉決策圖EVBDD和邊值多值決策圖EVMDD進行了系統的介紹和分析,特別提出了邊值多值決策圖在動態故障樹方面的應用.EVMDD可以更加緊湊的表示整個系統,綜合運用組合方法和狀態空間方法,這不僅使得狀態空間爆炸問題得到緩解,也使得計算速度得到提升,可以廣泛應用于現實生活中的多狀態系統和多功能動態軟件的性能分析等方面[17,18].