基于灰色關聯分析的LS-SVM的高鐵客流量預測

趙盼 張浩倫 耿立艷 張占福

摘要：結合灰色關聯分析（GRA）和最小二乘支持向量機（LS-SVM），構建基于GRA的LS-SVM高鐵客流量預測模型（GRA-LS-SVM）。將高鐵客流量的影響因素初步設為17項，利用灰色關聯分析從中選取主要影響因素，并將其作為輸入變量，構建LS-SVM。以我國高鐵客流量數據為例，驗證GRA-LS-SVM的有效性。結果顯示，GRA-LS-SVM不僅簡化了模型結構，而且提高了高鐵客流量預測精度。

關鍵詞：高鐵客流量 灰色關聯分析 最小二乘支持向量機

1.引言

隨著各種交通工具的發展，客運市場競爭加劇，消費者對于出行的需求正在發生著變化。作為我國傳統的交通工具——鐵路運輸業出現了前所未有的挑戰，滿足旅客的出行要求是保持運輸市場份額的重要條件。同時人們對于出行的成本、時間、服務質量等多方面做出了更高的要求，因此我國高速鐵路旅客運輸量在客運總量中所占的比例逐年增加，高速鐵路已經逐漸成為人們出行的一種必要選擇方式。隨著高鐵數據的涌現，如何通過對數據的深層次挖掘，提升高鐵客流量預測精度，是一個亟待解決的重要課題。

高鐵客流量在多種影響因素作用下呈現非線性的變動，且較為復雜，為了提高預測精度，劉強、陸化普（2011）等針對區域鐵路客運量數據樣本少的問題，構建了基于支持向量機（SVM）的區域運量滾動預測模型，通過實例分析證明該模型的預測精度優于傳統預測方法[1]，夏國恩等（2010）提出的加權SVM，通過賦予懲罰因子不同的加權系數，獲得了比SVM和BP神經網絡更優的預測效果[2]，張蕾、孫德山（2018）將灰色關聯分析方法與支持向量機預測方法相結合預測鐵路貨運量，預測較為準確[3]。可見，SVM是預測客運、貨運量的重要方法。本文將SVM的改進形式最小二乘支持向量機（LS-SVM）與灰色關聯分析相結合，預測高鐵客流量的預測，期望為高鐵的修建、管理及運營提供理論與方法指導。

2. LS-SVM

2.1 LS-SVM算法

支持向量機最適合于小樣本的學習環境。它的關鍵在于要找出所有的支持向量，從這些支持向量，就能得出最優分隔超平面了。這一做法讓人聯想到普通信號的處理。對于一個信號，其結構都是真實信號加上各種噪聲。做信號處理時，目的就是為了削弱噪聲的影響，從而得出真實的信號值。支持向量機與信號濾波有相似之處，在樣本里，除了支持向量的那些點就像是信號里的噪聲，支持向量恰對應于信號中的真實成分，支持向量機里尋找最優超平面恰好就是信號處理時要極大化削弱噪聲的影響。

本文所采用的最小二乘支持向量機便是一種被最為廣泛采用的方法，其對非線性問題的處理有較好的準確度及精度提升。與人工神經網絡比，它能克服訓練時間長、訓練結果存在隨機性以及過學習的不足。

設樣本為n維向量，其中1個樣本及其值表示為

首先用非線性映射把樣本從原空間映射到特征空間）。在這個高維特征空間中構造最優決策函數，非線性估計函數就轉化為高維特征空間中的線性估計函數。根據風險最小化原則，設，其中控制模型的復雜度，c為正規化參數，為誤差控制參數，也即不敏感損失函數。常用的損失函數有線性損失函數，二次損失函數，huber損失函數。選取不同的損失函數可構造不同形式的支持向量機。最小二乘支持向量機選用的損失函數為誤差的二次項，故優化問題為

（1）

用拉格朗日法求解這個優化問題

（2）

其中，是拉格朗日乘子，根據優化條件：

（3）

可得

（4）

定義核函數，是滿足Mercer條件的對稱函數。根據（4），優化問題轉化為求解線性方程：

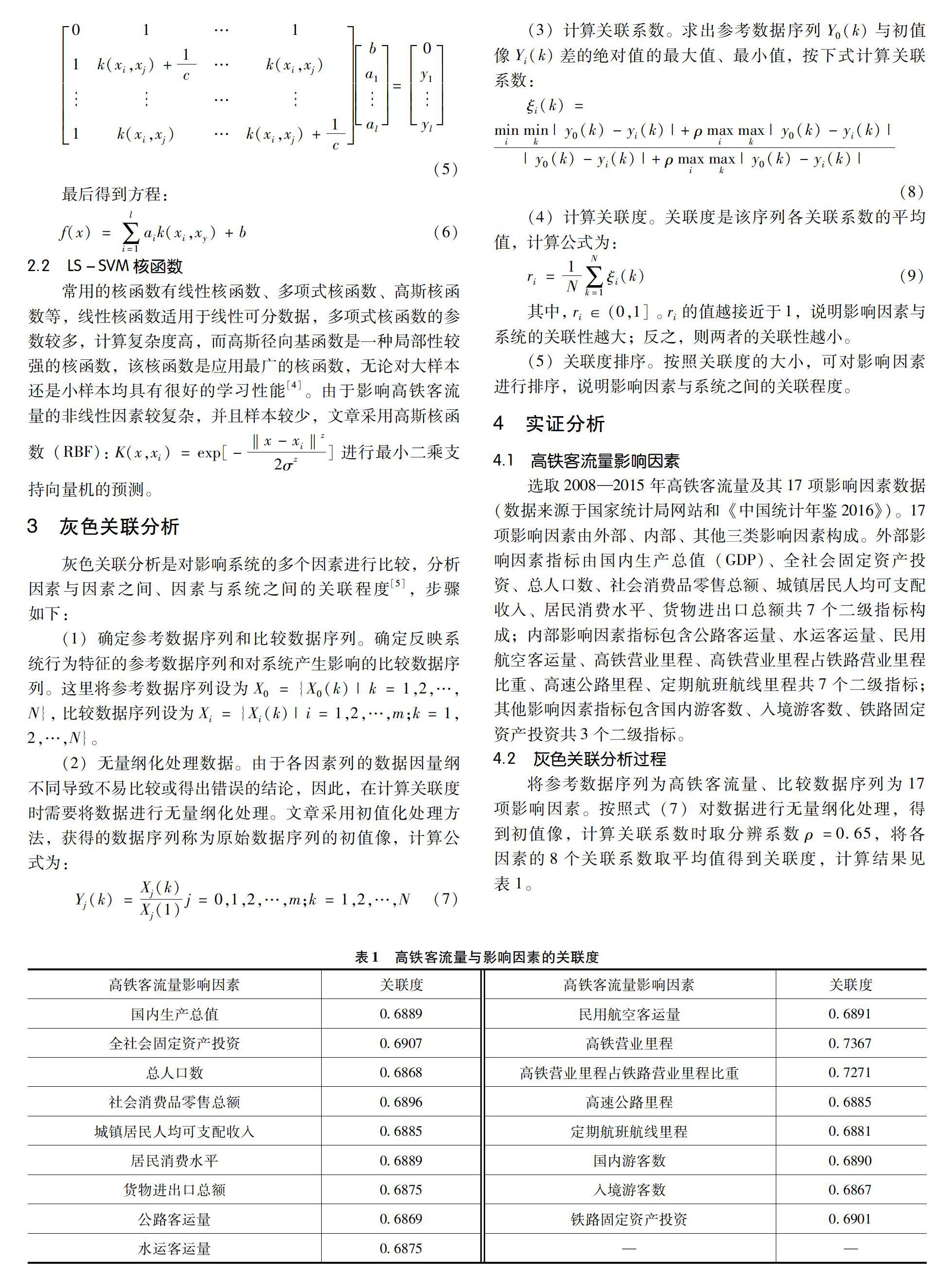
= ????????????????（5）

最后得到方程： ?????????????????????????????（6）

2.2LS-SVM核函數

常用的核函數有線性核函數，多項式核函數，高斯核函數等，線性核函數適用于線性可分數據，多項式核函數的參數較多，計算復雜度高，而高斯徑向基函數是一種局部性較強的核函數，該核函數是應用最廣的核函數，無論對大樣本還是小樣本均具有很好的學習性能[4]。由于影響高鐵客流量的非線性因素較復雜，并且樣本較少，本文采用高斯核函數（RBF）：進行最小二乘支持向量機的預測。

3.灰色關聯分析

灰色關聯分析是對影響系統的多個因素進行比較，分析因素與因素之間、因素與系統之間的關聯程度[5]，步驟如下：

（1）確定參考數據序列和比較數據序列。確定反映系統行為特征的參考數據序列和對系統產生影響的比較數據序列。這里將參考數據序列設為，比較數據序列設為。

（2）無量綱化處理數據。由于各因素列的數據因量綱不同導致不易比較或得出錯誤的結論，因此，在計算關聯度時需要將數據進行無量綱化處理。本文采用初值化處理方法，獲得的數據序列稱為原始數據序列的初值像，計算公式為：

（7）

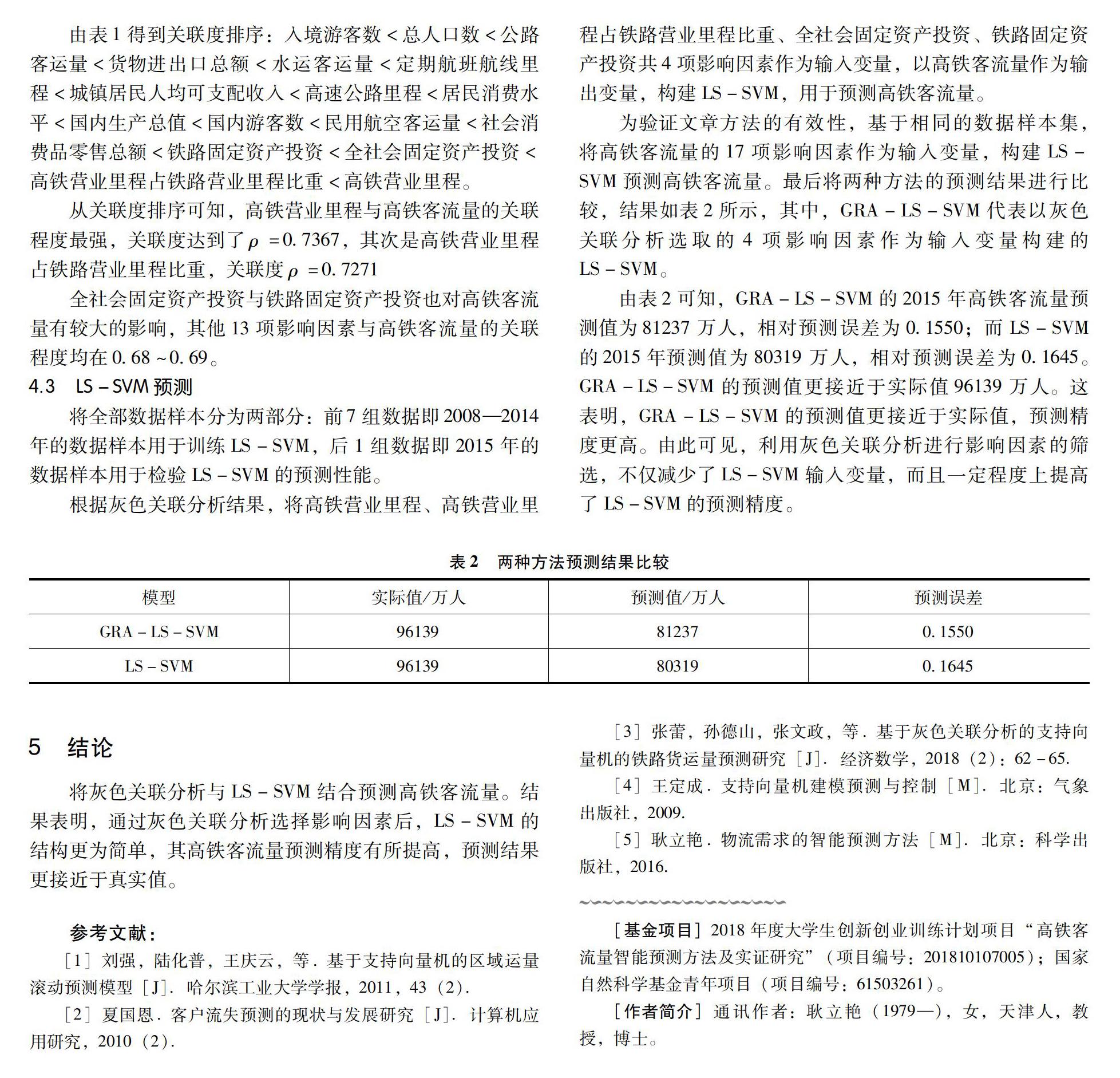
（3）計算關聯系數。求出參考數據序列與初值像差的絕對值的最大值、最小值，按下式計算關聯系數：

（8）

（4）計算關聯度。關聯度是該序列各關聯系數的平均值，計算公式為：

（9）

其中，。的值越接近于1，說明影響因素與系統的關聯性越大;反之，則兩者的關聯性越小。

（5）關聯度排序。按照關聯度的大小，可對影響因素進行排序，說明影響因素與系統之間的關聯程度。

4.實證分析

4.1高鐵客流量影響因素

選取2008～2015年高鐵客流量及其17項影響因素數據（數據來源于國家統計局網站和《中國統計年鑒2016》）。17項影響因素由外部、內部、其他三類影響因素構成。外部影響因素指標由國內生產總值（GDP）、全社會固定資產投資、總人口數、社會消費品零售總額、城鎮居民人均可支配收入、居民消費水平、貨物進出口總額共7個二級指標構成;內部影響因素指標包含公路客運量、水運客運量、民用航空客運量、高鐵營業里程、高鐵營業里程占鐵路營業里程比重、高速公路里程、定期航班航線里程共7個二級指標;其他影響因素指標包含國內游客數、入境游客數、鐵路固定資產投資共3個二級指標。

4.2灰色關聯分析過程

將參考數據序列為高鐵客流量、比較數據序列為17項影響因素。按照公式（7）對數據進行無量綱化處理，得到初值像，計算關聯系數時取分辨系數=0.65，將各因素的8個關聯系數取平均值得到關聯度，計算結果見表1。

由表1得到關聯度排序：入境游客數<總人口數<公路客運量<貨物進出口總額<水運客運量<定期航班航線里程<城鎮居民人均可支配收入<高速公路里程<居民消費水平<國內生產總值<國內游客數<民用航空客運量<社會消費品零售總額<鐵路固定資產投資<全社會固定資產投資<高鐵營業里程占鐵路營業里程比重<高鐵營業里程

從關聯度排序可知，高鐵營業里程與高鐵客流量的關聯程度最強，關聯度達到了=0.7367，其次是高鐵營業里程占鐵路營業里程比重，關聯度=0.7271，

全社會固定資產投資與鐵路固定資產投資也對高鐵客流量有較大的影響，其他13項影響因素與高鐵客流量的關聯程度均在0.68-0.69之間。

4.3 LS-SVM預測

將全部數據樣本分為兩部分：前7組數據即2008～2014年的數據樣本用于訓練LS-SVM，后1組數據即2015年的數據樣本用于檢驗LS-SVM的預測性能。

根據灰色關聯分析結果，將高鐵營業里程、高鐵營業里程占鐵路營業里程比重、全社會固定資產投資、鐵路固定資產投資共4項影響因素作為輸入變量，以高鐵客流量作為輸出變量，構建LS-SVM，用于預測高鐵客流量。

為驗證本文方法的有效性，基于相同的數據樣本集，將高鐵客流量的17項影響因素作為輸入變量，構建LS-SVM預測高鐵客流量。最后將兩種方法的預測結果進行比較，結果如表2所示，其中，GRA-LS-SVM代表以灰色關聯分析選取的4項影響因素作為輸入變量構建的LS-SVM。

由表2可知，GRA-LS-SVM的2015年高鐵客流量預測值為81237萬人，相對預測誤差為0.1550;而LS-SVM的2015年預測值為80319萬人，相對預測誤差為0.1645。GRA-LS-SVM的預測值更接近于實際值96139萬人。這表明，GRA-LS-SVM的預測值更接近于實際值，預測精度更高。由此可見，利用灰色關聯分析進行影響因素的篩選，不僅減少了LS-SVM輸入變量，而且一定程度上提高了LS-SVM的預測精度。

表2 兩種方法預測結果比較

模型 實際值/萬人 預測值/萬人 預測誤差

GRA-LS-SVM 96139 81237 0.1550

LS-SVM 96139 80319 0.1645

5.結論

將灰色關聯分析與用LS-SVM結合預測高鐵客流量。結果表明，通過灰色關聯分析選擇影響因素后，LS-SVM的結構更為簡單，其高鐵客流量預測精度有所提高，預測結果更接近于真實值。

參考文獻

[1]劉強，陸化普，王慶云，等.基于支持向量機的區域運量滾動預測模型[J].哈爾濱工業大學學報，2011，43（2）

[2]夏國恩.客戶流失預測的現狀與發展研究[J].計算機應用研究，2010（2）

[3]張蕾，孫德山，張文政，等.基于灰色關聯分析的支持向量機的鐵路貨運量預測研究.經濟數學，2018（2）：62-65

[4]王定成.支持向量機建模預測與控制[M].北京：氣象出版社，2009.

[5]耿立艷.物流需求的智能預測方法[M].北京：科學出版社，2016.

基金項目：2018年度大學生創新創業訓練計劃項目“高鐵客流量智能預測方法及實證研究”（項目編號：201810107005）;國家自然科學基金青年項目（項目編號：61503261）。

作者簡介：通訊作者：耿立艷（1979-），女，天津人，教授，博士。