多胞材料的動態應力應變狀態及其一致近似關系*

王 鵬，朱長鋒，鄭志軍，虞吉林

(1.中國科學技術大學近代力學系中國科學院材料力學行為和設計重點實驗室,安徽 合肥 230026;2.中國工程物理研究院總體工程研究所,四川 綿陽 621999)

多胞材料在高速沖擊下具有變形局部化的典型特征。Reid等[1-2]研究了由圓環組成的一維系統的動態沖擊行為，提出了“結構沖擊波”的概念，并在對木材的動態壓潰實驗中證實了壓潰帶的沖擊波傳播特征。Zheng等[3]、Liu等[4]在對隨機蜂窩的動態沖擊中觀察到3種變形模式，即均勻模式、過渡模式和沖擊模式。張新春等[5]、胡玲玲等[6]探討了胞元構型對蜂窩結構動態沖擊性能的影響。Zou等[7]認為蜂窩中傳播的沖擊波波陣面在高速沖擊下具有胞元尺寸的寬度。Liao等[8]采用了局部應變場計算方法表征了蜂窩鋁中一維沖擊波的傳播并得到了沖擊波速度的大小。一系列的一維沖擊波模型被發展來表征多胞材料中塑性壓潰行為，如R-PP-L模型(率無關、剛性-理想塑性-鎖定假設)[2,9-10]和R-PH模型(率無關，剛性-塑性硬化假設)[11-13]。然而，大部分的沖擊波模型都是基于準靜態名義應力-應變曲線得到的，直接得到動態的應力應變關系在實驗上是困難的。

多胞材料在動態沖擊下存在變形局部化和應力增強等現象，名義應力應變曲線失去了物理意義[4]。Zheng等[13]通過對泡沫鋁的三維細觀有限元模型的分析得到了波后應力應變狀態點，并提出了D-R-PH(動態，剛性-塑性硬化)模型來表征動態應力-應變行為。Barnes等[14]、Sun等[15]分別對開孔泡沫和閉孔泡沫進行實驗和數值研究，也得到了多胞材料的動態應力應變狀態。但這些研究都是針對沖擊模式下的應力應變狀態，對過渡模式下的應力應變狀態的認識仍然不清楚。此外，文獻[13-15]中波后應力都是由撞擊端的名義應力得到的，缺少對材料內部局部應力信息的直接表征。

認識多胞材料在中速過渡模式下的應力應變行為，對于完整地理解多胞材料的動態本構關系有重要意義。本文中將采用截面應力計算方法研究基于細觀有限元模型的隨機蜂窩結構在恒速沖擊下的應力分布，分析沖擊波在隨機蜂窩中的傳播特性，表征隨機蜂窩的動態應力應變關系。

1 數值模型

1.1 細觀有限元模型

采用二維Voronoi技術構造隨機蜂窩結構，詳細建模過程參見文獻[3]。如圖1，蜂窩試件的長和寬均為50 mm，試件的不規則度為0.3，由500個胞元組成。試件相對密度ρ0/ρs= 0.1，其中ρ0為蜂窩試樣變形前的初始密度，ρs為基體材料的密度。蜂窩試件的平均胞元尺寸約為2.5 mm，其值定義為與平均胞元面積相等的圓的直徑。

圖1 Voronoi蜂窩試件細觀有限元模型Fig.1 A cell-based finite element model of a Voronoi honeycomb specimen

采用ABAQUS/Explicit有限元軟件對蜂窩材料的恒速壓潰過程進行數值模擬。胞壁材料由S4R殼單元(4節點，減縮積分、沙漏控制、有限膜應變)進行模擬。通過網格收斂性分析將模型劃分了10 480個殼單元，平均單元長度約為0.2 mm。基體材料屬性設置為彈性-理想塑性，材料參數設置為泊松比ν= 0.3，彈性模量E= 66 GPa，屈服應力σy= 175 MPa，基體密度ρs= 2 700 kg/m3。所有接觸面均定義為通用接觸，摩擦因數取為0.02。為了模擬面內變形，模型中所有節點的面外變形均被限制。

蜂窩試件的左右兩端設置兩個剛性面，左側剛性面以恒定不變的速度v沿x方向向右壓縮試件。在壓縮過程中右側剛性板為固支端，如圖1所示。

1.2 截面應力計算方法

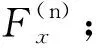
(1)

(2)

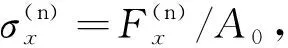
2 結 果

2.1 一維應力分布

沖擊速度分別為200和50 m/s時的應力分布如圖2所示。在任意名義應變時刻下，應力會在某個位置發生陡然減小，并且這個位置隨著名義應變的增大往試件右側移動。這說明在高速和中速撞擊下試件內均存在沖擊波的傳播，應力發生急劇變化的位置即為沖擊波波陣面的位置，中速撞擊下的波陣面區域相較于高速撞擊更加平緩。從圖2可以明顯地觀察到應力增強現象，跨過沖擊波陣面，應力由波前應力迅速增加到波后應力并幾乎保持不變。

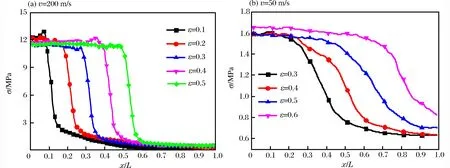
圖2 兩種沖擊速度下的應力分布圖Fig.2 One-dimensional stress distributions at two impact velocities

2.2 基于應力分布得到沖擊波速度

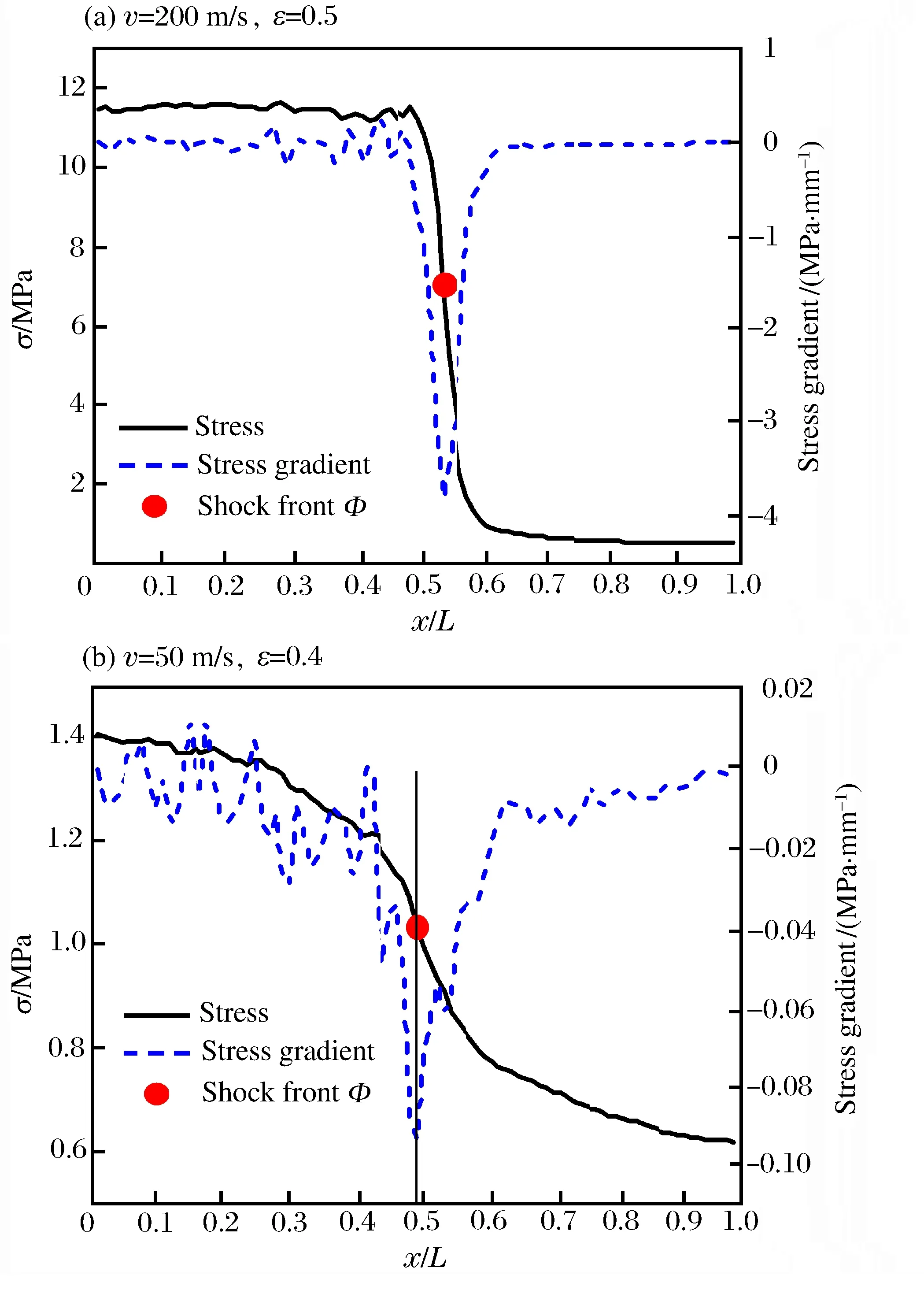
圖3 一維的應力分布及其應力梯度分布Fig.3 One-dimensional stress distributions and the corresponding stress gradients

可以由應力分布梯度來確定沖擊波波陣面Φ的位置，如圖3所示。應力分布梯度反映了一維應力在加載方向上的變化，在應力梯度絕對值達到最大的拉格朗日坐標位置，應力變化最快，這個位置即為當前時刻沖擊波波陣面的位置。中速和高速壓潰下波陣面位置均可以采用此方法得到。不同沖擊速度下得到的波陣面位置隨沖擊時間變化關系如圖4所示。在恒速壓縮情形下，沖擊波的波陣面位置與沖擊時間關系為線性關系。可通過對線性關系擬合得到的斜率來預估沖擊波速度。從圖4中可以看出，沖擊速度越大，斜率越大，則相應的沖擊波速度也越大。

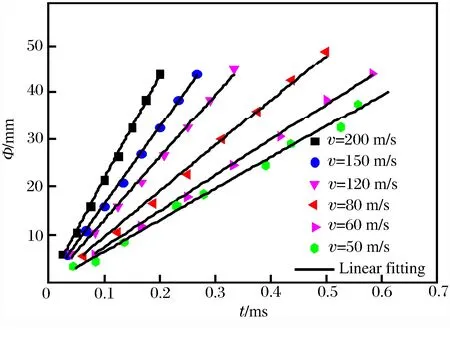
圖4 不同沖擊速度下沖擊波位置隨時間的關系Fig.4 Variation of shock front position with impact time at different impact velocities

2.3 一維沖擊波理論

除了由有限元結果直接得到的應力信息來得到沖擊波速度之外，一維沖擊波理論也可以對蜂窩中的沖擊波傳播行為進行描述。由應力波理論[17]，跨波陣面的質量和動量守恒關系分別為:

vB(t)-vA(t)=vs(t)(εB(t)-εA(t))

(3)

σB(t)-σA(t)=ρ0vs(t)(vB(t)-vA(t))

(4)

式中:vs(t)是沖擊波速度,σB、εB、vB為波后方的應力、應變和速度，σA、εA、vA為波前方的應力、應變和速度。聯立這兩個守恒關系可以得到沖擊波速度與波前波后應力、應變的關系為：

(5)

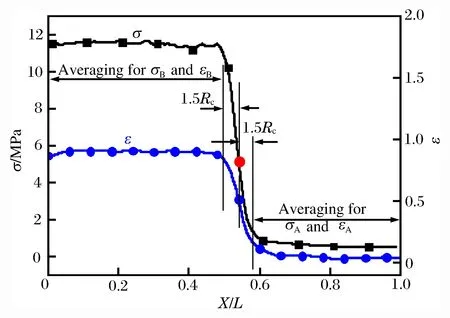
圖5 一維應力和應變分布及其理想化Fig.5 One-dimensional stress and strain distributions and the idealizations

如果能直接從有限元結果中得到波前和波后應力/應變信息，就可以由式(5)計算得到沖擊波速度的大小。為了簡便，這里將這種結合沖擊波理論和數值模擬結果的方法叫做一維沖擊波理論方法。

通過對一維應力和應變分布求平均值，可以得到波前和波后的應力和應變，如圖5所示。圖中一維應變分布采用文獻[8]提出的局部應變計算方法得到。在求平均的過程中，為了消除沖擊波波陣面平均效應的影響，將緊鄰波陣面附近1.5倍胞元半徑Rc內的數據排除掉。波后應力和應變信息由沖擊端到Φ-1.5Rc區域內平均得到，波前應力應變信息由Φ+1.5Rc到支撐端區域平均得到。再由式(5)就可以得到不同沖擊速度下的沖擊波速度。

2.4 沖擊波速度的比較

通過截面應力和局部應變場等有限元方法以及一維沖擊波理論方法都可以得到沖擊波速度。此外，也可由已有的沖擊波模型得到沖擊波速度的大小。由R-PP-L模型[2]得到的沖擊波速度為:

vs=v/εL

(6)

式中:εL為多胞材料的鎖定應變。由R-PH模型[13]得到的沖擊波速度為:

(7)

式中:C為多胞材料的塑性硬化參數。在本文中，εL=0.64，C=0.226 MPa。

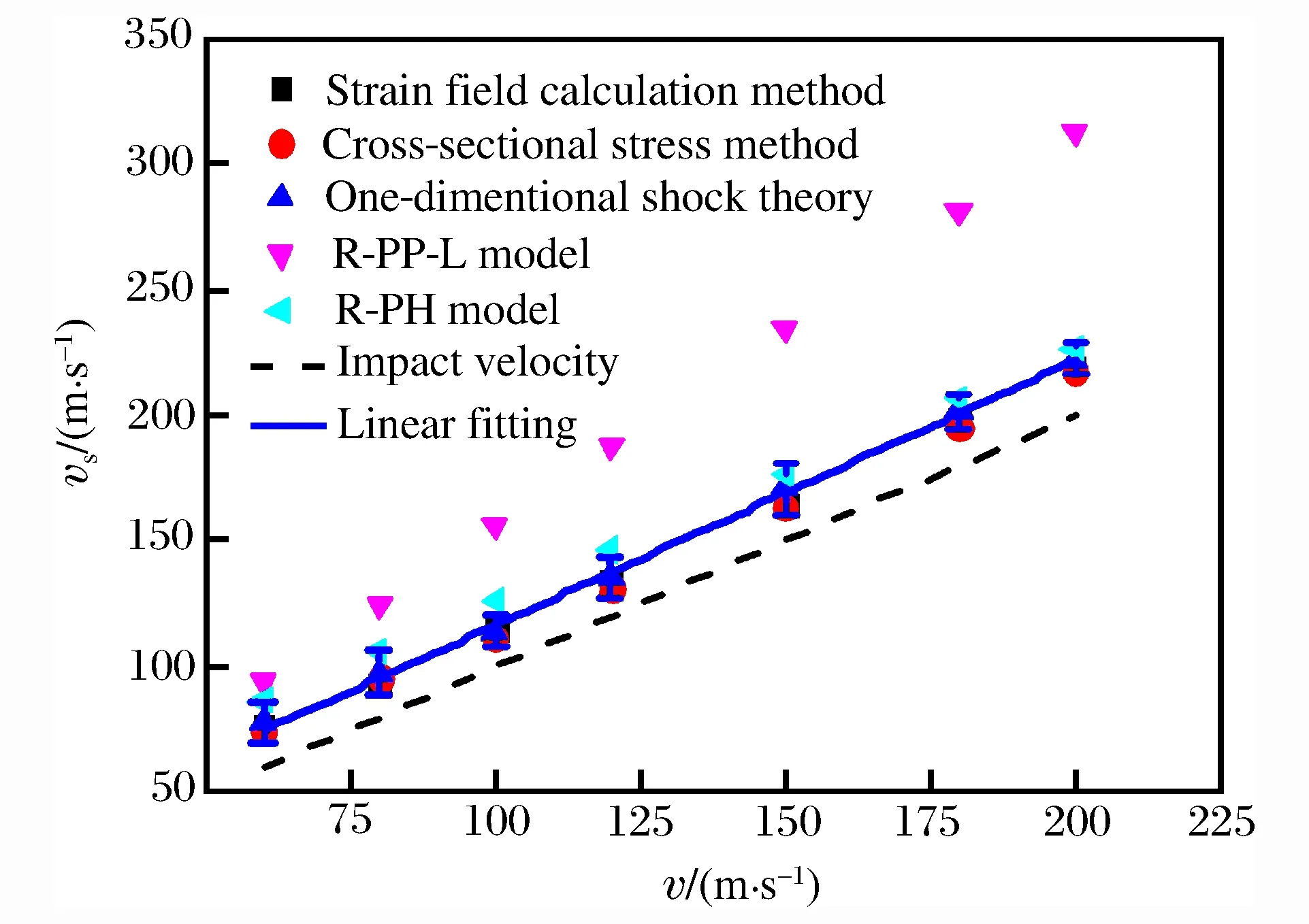
圖6 不同方法得到的沖擊波速度的比較Fig.6 Comparison of shock wave speeds obtained using different methods

由不同方法得到的沖擊波速度如圖6所示。由一維沖擊波理論方法以及R-PH沖擊波模型得到的沖擊波速度比較接近有限元方法得到的沖擊波速度，并且與沖擊速度的差值均為一個常值，即材料沖擊參數。然而由R-PP-L模型預估得到的沖擊波速度明顯高于有限元結果。這是由于R-PP-L模型采用的是鎖定不變的壓實應變，實際上其值小于動態壓潰的壓實應變。由質量守恒關系可以發現，壓實應變越小，沖擊波速度越大。R-PH模型中的壓實應變是隨沖擊速度變化的動態應變，因此更加適合描述多胞材料在動態壓潰下的沖擊波傳播。

3 分析和討論

3.1 沖擊波速度的一致近似

前文中通過應力分布得到了高速沖擊下的沖擊波速度與沖擊速度的關系。在中等沖擊速度下，仍然可以觀察到沖擊波傳播的現象[4,8]，因此仍然采用應力梯度分布方法來確定沖擊波速度的大小，結果見圖7。當沖擊速度很高的時候，沖擊波速度與沖擊速度呈線性關系并且兩者之間的差值幾乎為一個常數[13]。但隨著沖擊速度的減小，沖擊波速度趨近于常數。因此，沖擊波速度對沖擊速度的一階導數在低速和高速下分別趨于0和1，從低速到高速的完整曲線具有明顯的S型特征。利用S函數(sigmoid function)，沖擊波速度對沖擊速度的一階導數可以寫作：

(8)

式中:a和b為待定參數。上式的積分形式可以寫作：

(9)

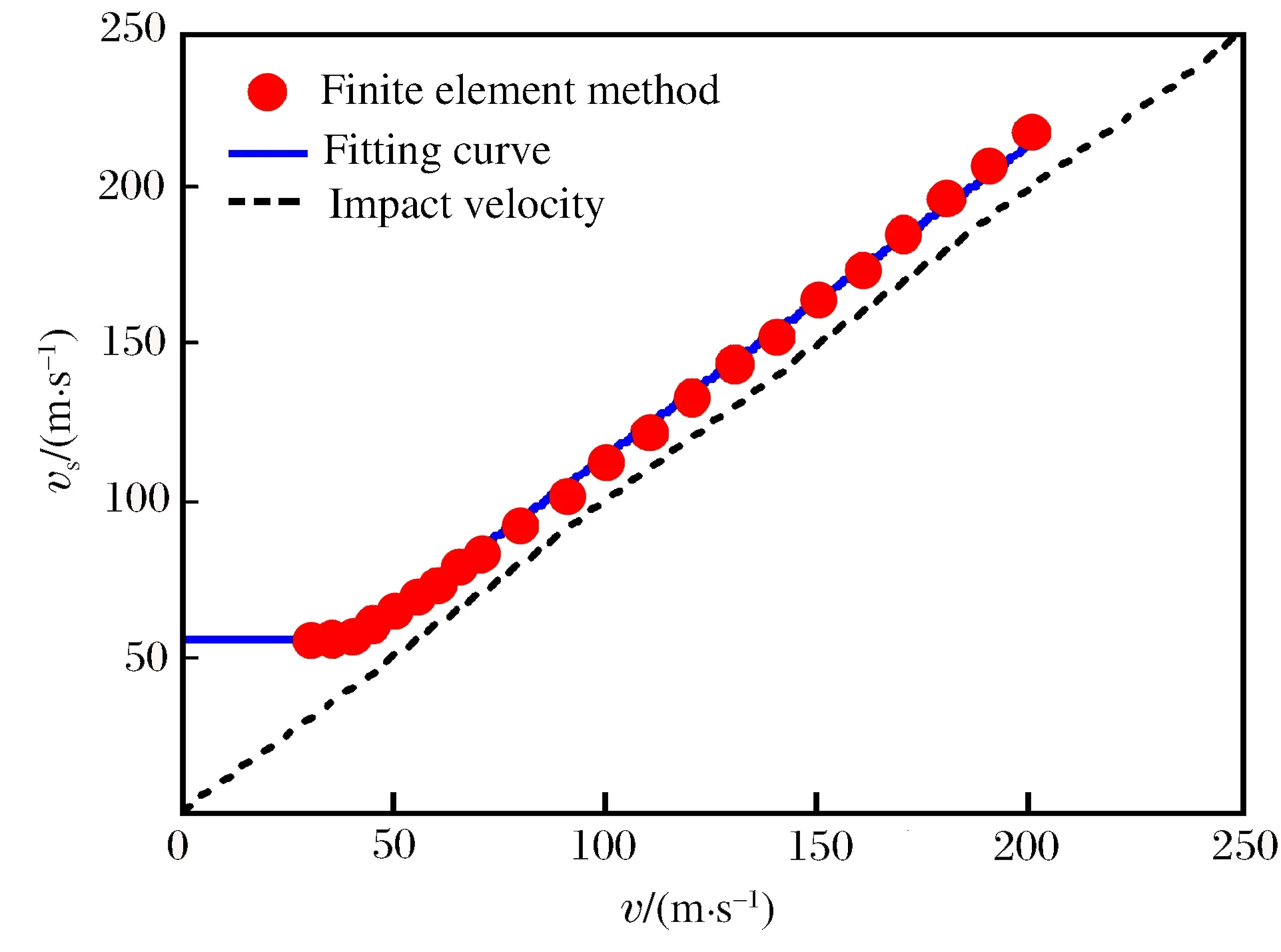
圖7 沖擊波速度與沖擊速度的關系Fig.7 Variations of the shock wave speed with the impact velocity

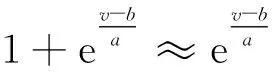
3.2 動態應力應變狀態的一致近似

在本文中考察的恒速沖擊情形中，若取εA=0,vA=0,vB=v和σA=σ0，由跨波陣面的守恒關系式(3)和(4)有:

(10)

將式(9)代入上式，可得：

(11)

與有限元結果的比較如圖8所示，圖中虛線對應于式(11)。可見式(11)與有限元結果存在一定的誤差。事實上，在恒速沖擊下，沖擊波波陣面前方的應變和粒子速度不能直接忽略。

圖9給出了不同沖擊速度下試件中的速度分布情況，局部粒子速度在沖擊波波陣面位置附近約兩個胞元區間內急劇變小。當沖擊速度為中等大小時，波陣面位置處的粒子速度變化更為平緩。整個波前區域處于低速狀態，近似呈線性分布，與沖擊速度的大小關系不大。沖擊波前方的粒子速度和變形不能忽略，可以通過圖9估算vA≈10 m/s，初始壓潰應變εA取準靜態實驗中常用的ε0=0.02。因此，由跨波陣面的守恒關系式(3)和(4)有:

(12)

將式(9)代入上式，可得:

(13)

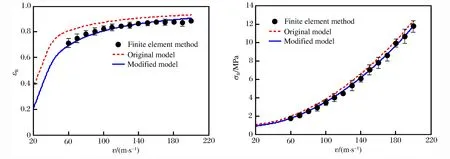
圖8 波后應變和波后應力隨沖擊速度的變化Fig.8 Variations of strain and stress behind shock front with impact velocity

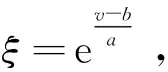
(14)

式中:α=vA/a,β=b/a,γ=c/a和B=ρ0a2。因此，式(14)給出恒速沖擊下動態應力應變狀態的一致近似關系。準靜態和動態應力應變關系的比較如圖10所示。在圖10中，準靜態應力應變曲線及動態應力應變狀態點由有限元計算得到，動態應力應變曲線由式(14)得到。在動態應力應變關系的曲線上的每個點都對應著特定的一個沖擊速度。在高應變情形下，動態應力應變關系位于準靜態曲線右側，這與已有文獻中的結論一致。隨著應變的減小，動態的應力應變關系逼近準靜態應力應變曲線。

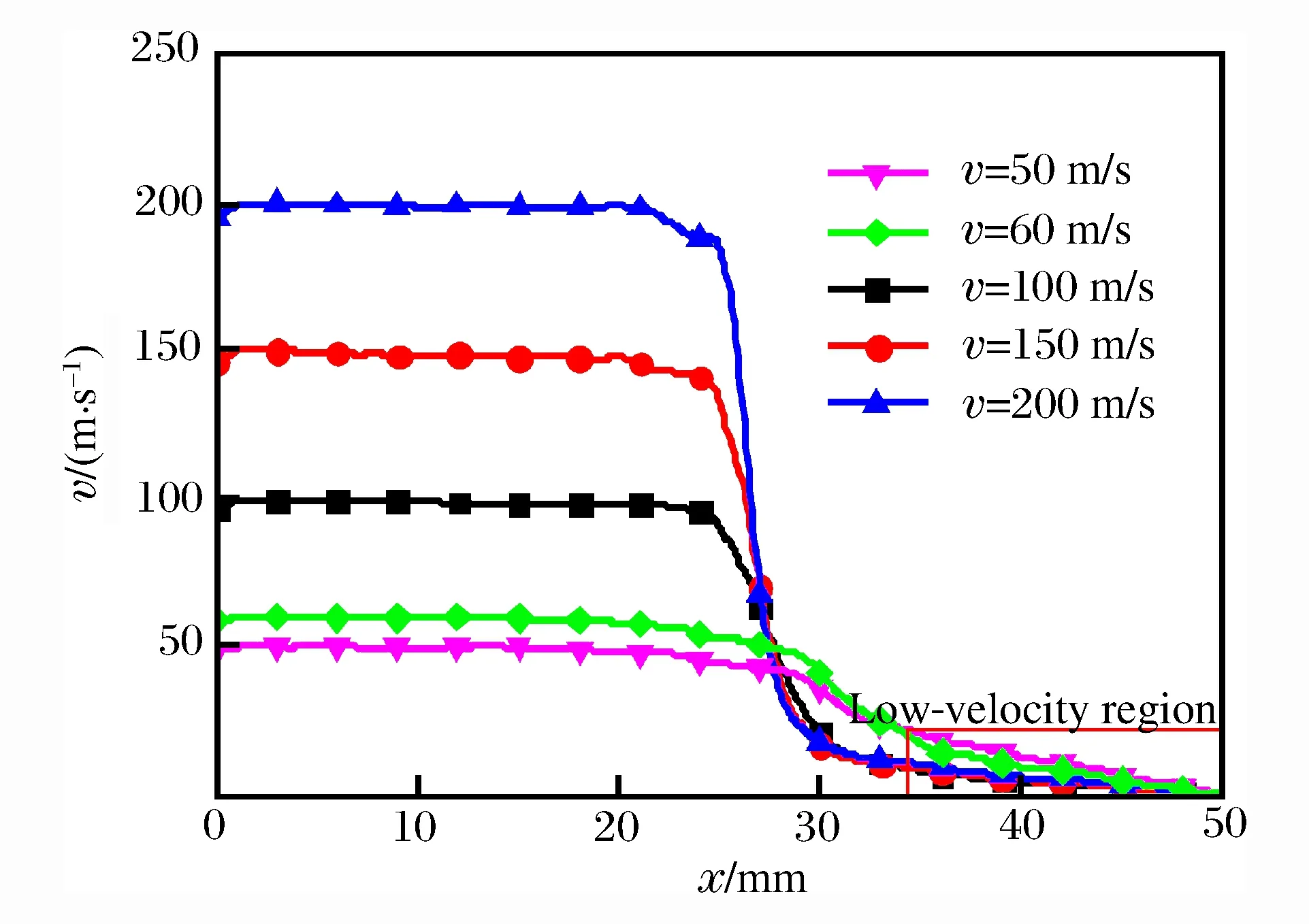
圖9 不同沖擊速度下的速度分布Fig.9 Velocity distributions at different impact velocities

圖1 0 準靜態及動態應力應變關系Fig.10 Quasi-static and dynamic stress-strain relations

4 結 論

采用細觀有限元模型研究了隨機蜂窩結構在恒速沖擊下的動態性能，采用截面應力計算方法得到了隨機蜂窩試件內的應力分布和沖擊波速度，比較了高速沖擊下由不同方法得到的沖擊波速度與沖擊速度的關系。結果表明，R-PP-L模型高估了沖擊波速度，但R-PH模型以及一維沖擊波理論得到的沖擊波速度與有限元模擬得到的結果接近。在沖擊速度很高的時候，沖擊波速度與沖擊速度的關系趨于線性，但隨著沖擊速度的減小，沖擊波速度不斷減少并趨于常數。最后，發展了可以表征沖擊波速度與沖擊速度的關系的一致近似模型，并基于一維沖擊波理論發展了動態應力應變關系的一致近似模型。這個模型可以對多胞材料在過渡模式及沖擊模式下的動態壓潰行為進行表征。