C H F=C H C l分子的特性研究

梁冬梅 荊 濤 ＊ 孫光宇

（1.凱里學院理學院，貴州 凱里 556011；2.貴州師范學院物理與電子工程學院，貴州 貴陽 550018）

0 引言

近年來的實驗和理論研究發現， 二鹵代乙烯類化合物順式構型的穩定性明顯優于反式構型的穩定性[1-4]。并且，樊曉偉等[5]對化合物二氟代乙烯使用不同的基組進行計算發現， 使用小基組計算的總能量和軌道能量并不收斂， 甚至會給出錯誤的能級排序， 而使用較大基組計算的數值更接近于實驗值。 因此， 為了給出正確的計算結果，本文使用與文獻[5]相同的基組進行計算。

1 理論和計算方法

外電場存在時，哈密頓量H 可用下式求出，H=H0+Hint， （1）

上式中Hint的含義為， 當分子處在偶極近似條件下，外電場和分子體系之間的相互作用。 其表達式為，Hint=-μ·F （2）

在（2）式中，變量μ 表示偶極矩。

若哈密頓量Hint為零，有H=H0， （3）

從Grozema 等[6-7]創立的模型看，有外電場存在時的激發能Eexc為，

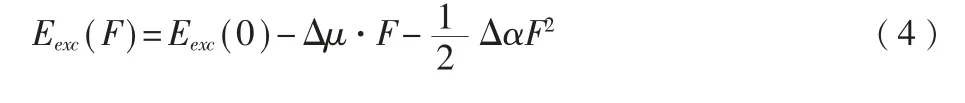
其中，在無外電場時的激發能，Eexc(F)=Eexc(0)。（5）

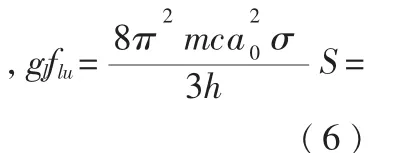
在上面的公式中包含了幾個重要的量， 它們分別是加權因子、線強度和波數，用字母表示為gl、S、σ，加權因子的大小為1，線強度的單位為e2a2

0。

按照CHF=CHF 分子的標準坐標， 在B3LYP/6-311++G(3df, 3pd)基組的基礎上對該分子的基態結構進行優化， 在此基礎上對其激發態能量等物理量進行了計算。 所有計算均在Gaussian03 軟件包[9]進行。

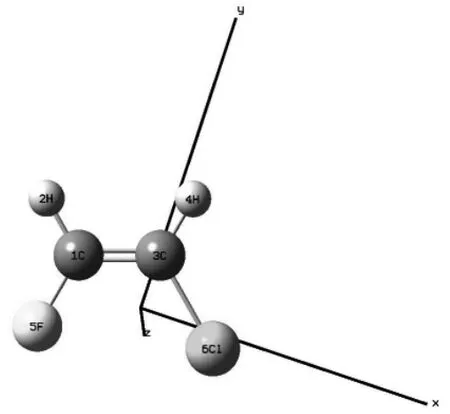
圖1 CHF=CHCl 分子的基態結構

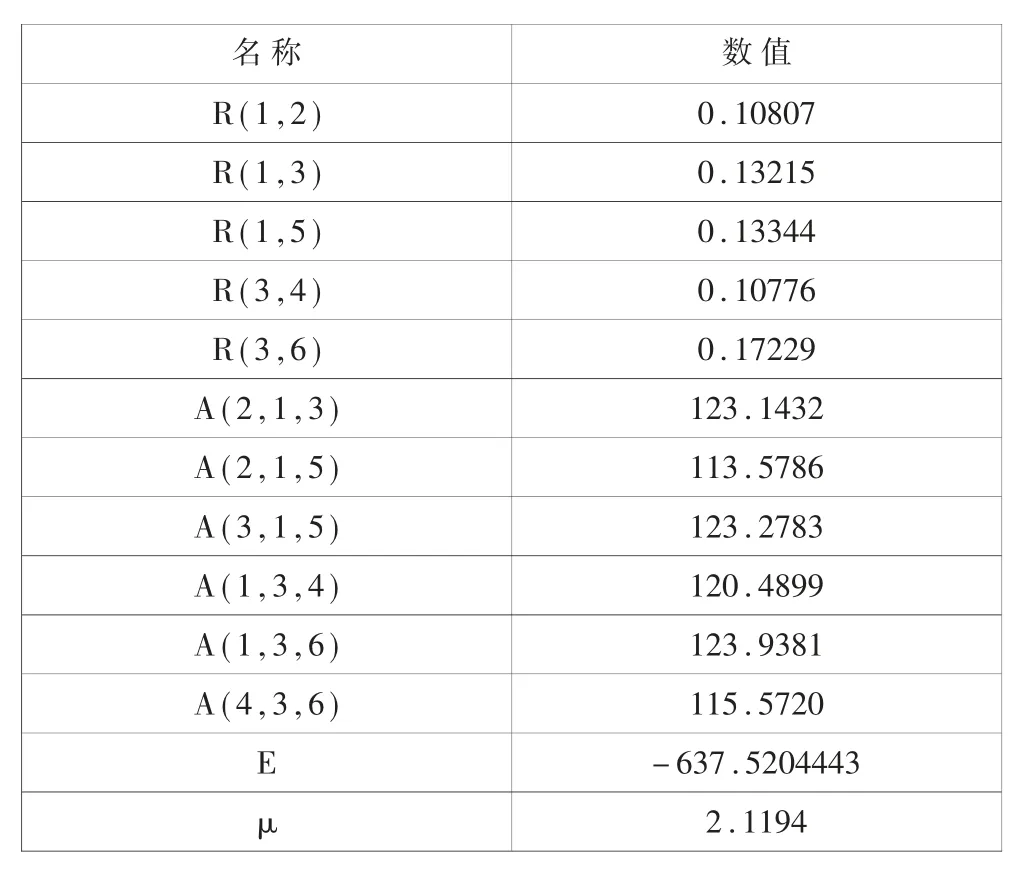
表1 優化的CHF=CHCl 分子基態鍵長(R/nm)、鍵角(A/deg)、總能量(E/a.u.)和偶極矩(μ/debye)

2 計算結果與討論

2.1 CHF=CHCl 分子的基態穩定構型

CHF=CHCl 分子的結構如圖1 所示。采用密度泛函理論(DFT)中的B3LYP，以6-311++G(3df,3pd)作為基函數，對其進行結構優化，得到該分子的基態鍵長、鍵角和總能，如表1 所示。

從表1 可以看出，分子的鍵長在0.10776～0.17229 nm之間變化，鍵角在113.5786～123.2783deg 之間變化，基態總能量為-637.5204443 a.u.，偶極矩為2.1194。

2.2 CHF=CHCl 分子的激發特性

在得到CHF=CHCl 分子穩定構型的基礎上， 采用CIS-B3LYP/6-311++G(3df, 3pd)方法研究了該分子的前8 個激發態的激發能E、激發波長λ 和振子強度，如表2 所示。

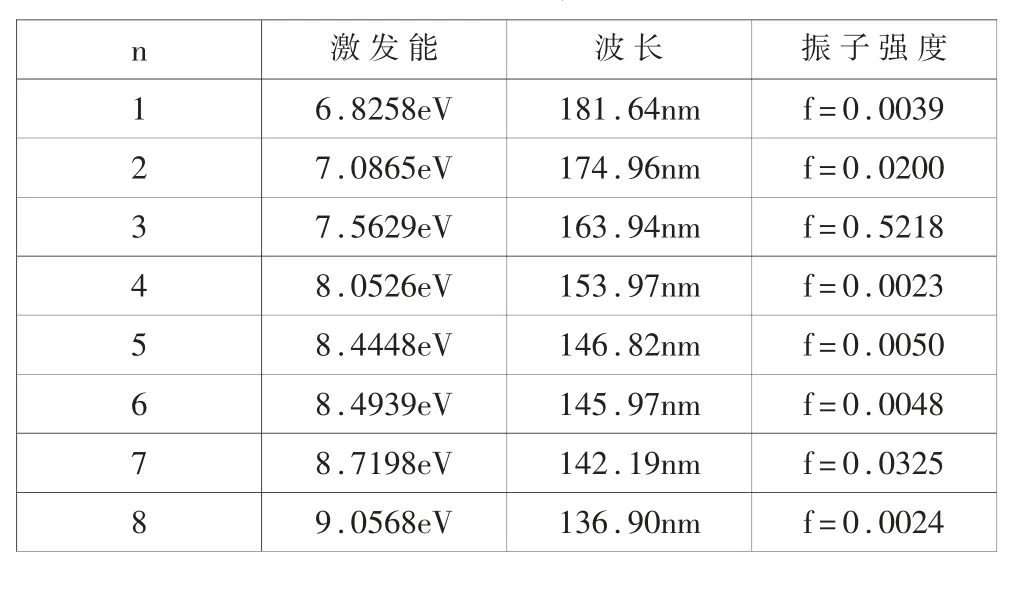
表2 分子CHF=CHCl 的激發態能量、激發波長和振子強度

通過表2 可以得出以下規律， 分子從基態躍遷到前8 個激發態， 激發態能量不斷增大， 激發態波長不斷減少。 如圖2 所示， 激發能從6.8258eV 增加到9.0568eV,而波長從181.64nm 下降到136.90nm。 振子強度就是振子數，從表2 可以看出，在從基態躍遷到激發態的過程中，振子強度并不為零，但大小不同。特別是從基態躍遷到第三個激發態， 振子強度f 達到了0.5218，有明顯的電子躍遷發生， 而從基態躍遷到第七個激發態，振子強度f 為0.0325，振子強度比較小，在實驗上即使有電子躍遷發生，也非常微弱，基本上觀察不到。 其它從基態躍遷到此激發態(n=1,2,4,5,6,8)，振子強度非常小，在實驗上觀察不到躍遷發生。

3 結論

本文采用B3LYP/6-311++G(3df,3pd)方法得到了CHF=CHCl 分子的基態穩定構型， 討論了分子的總能量、偶極矩和激發特性。 結論如下：

（1） 分 子 的 鍵 長 在0.10776 ～0.17229nm 之 間 變 化，鍵角在113.5786 ～123.2783deg 之間變化， 基態總能量為-637.5204443 a.u.，偶極矩為2.1194。

（2） 采用CIS-DFT 方法研究了分子的激發特性。分子的激發波長隨激發能的增大逐漸減小， 變化的快慢與激發能的變化快慢相關， 但并沒有在可見光區出現。 振子強度的大小不受激發能的影響， 電子躍遷的情況較為復雜。 從基態躍遷到第三激發態， 可以觀察到明顯的電子躍遷， 其它情況的振子強度較小， 基本上觀察不到躍遷現象發生。