四旋翼無人機軌跡跟蹤控制研究

秦澍祺 王國勝 梁 冰

（1.陸軍裝甲兵學院兵器與控制系，中國 北京 100072；2.江西理工大學信息工程學院，江西 贛州 341000）

0 引言

四旋翼是一個具有高機動的、非線性的、耦合的和欠驅動的系統。 所以許多研究人員設計了各種的線性、 非線性或者混合控制技術來控制四旋翼飛行器。比如傳統的PID 控制器[1]、反步法控制器[2]、滑膜控制器[3]、模型預測控制器[4]和的線性二次型[5]控制器等。這些控制器一般使用恒定的控制增益作為狀態反饋控制， 專注于對四旋翼無人機的穩態控制而不是軌跡或者目標跟蹤的精度。 本文則提出使用線性二次型跟蹤器（LQT），通過軌跡來調節控制增益從而更好追蹤期望軌跡。 同時與線性PID 和LQR 控制器作為對比，三者都在狀態估計上加入了相同的白噪聲干擾模擬實際環境。

1 模型建立與線性化

四旋翼飛行器模型考慮為線性定常系統， 狀態矩陣A、B、C 和D 都為靜態的不隨時間改變。定義如下：

x 為狀態向量，y 為輸出向量，u 為輸入向量，根據文獻[6]建立的四旋翼模型，線性化后狀態空間矩陣A、B 為：

其 中，12 維 狀 態 量[x y z u v w φ θ ψ p q r]T包括位置、速度、角度、角速度。CT，CM為升力系數和力矩系數，[Ixx,Iyy,Izz] 為轉動慣量，we為懸停時電機轉速，d為機臂長度，m,g 是質量與重力加速度。

2 LQT 控制器

首先需要將連續時間的線性定常系統離散化，將式（1）離散化，采樣時間為0.01 秒，離散系統如下所示：

在式（3）中，Ad,Bd和Cd分別為離散時間的狀態、輸入和輸出矩陣。“k”表示離散時間步長k=1,2,……，kf,k ∈Z+。 根據文獻[7-9]中離散時間線性二次跟蹤系統，定義最小化性能代價函數Jd：

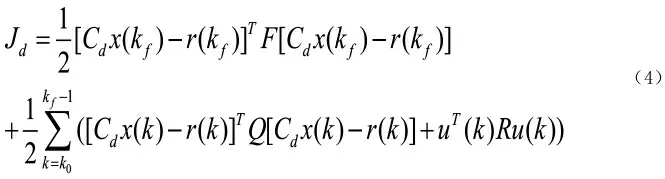
其中F 和Q 為狀態權重矩陣都為對稱的正半定矩陣，R 為控制權重矩陣也為對稱的正半定矩陣。r(k)是時變的軌跡狀態向量，k 為時間步長遵循期望的軌跡，kf為期望軌跡最后一個時間步長。

求解LQT 時變增益方程式組如下：

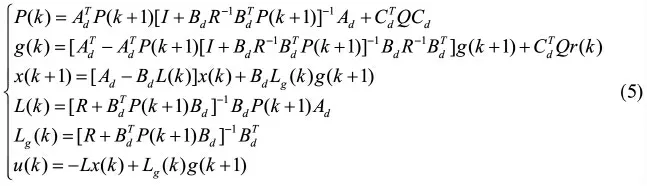
式（5）可以通過最終的狀態反向遞歸求解

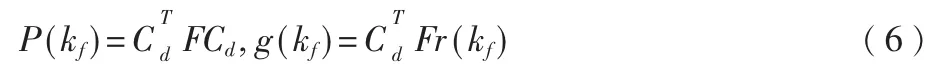
則最終控制輸入為：

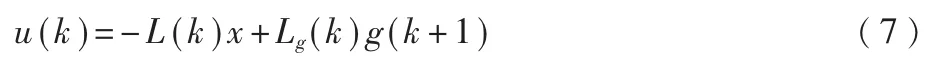
3 仿真實驗對比

四旋翼飛行器軌跡采用五階多項式規劃軌跡[10]，其中速度與加速度端點處為0。包括以下端點(0,0,0),(0,0,1),(1,0,1),(1,1,1),(0,1,1),(0,0,1),(0,0,0)，三個控制器仿真如下所示：

圖1 方向軌跡跟蹤仿真結果

上圖是在相同的白噪聲條件下使用三個控制器分別追蹤相同的軌跡。

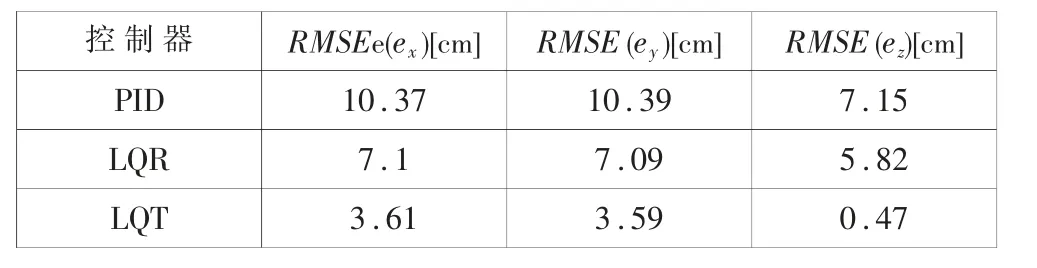
表1 控制器軌跡誤差均方根誤差

根據表1 均方根誤差對比，LQR 控制器在位置精度上相對于PID 分別提升了31.5%、31.8%、18.6%，而LQT 控制器在位置精度上相對于PID 則分別提升了65.2%、65.4%、93.4%。 因 此，LQT 控 制 器 在 軌 跡 跟 蹤精度上非常明顯的好于另外兩個控制器。

4 總結

本文主要針對四旋翼無人機估計追蹤設計了離散時間的LQT 控制器， 控制器使用了時變的控制增益。首先， 通過建立非線性的四旋翼動力學模型并將其線性化和離散化。 然后， 根據軌跡和利用黎卡提方程反向遞歸求出時變的最優控制增益。 從仿真結果來看，LQT 控制器在軌跡跟蹤精度上相對于PID 和LQR 控制器有大幅度的提升，該算法跟蹤軌跡較為精確。