基于TFN-AHP法的LID措施組合方案的評估方法

李 俊，吳 珊，侯本偉，曾小春

(1.北京工業大學建筑工程學院，北京 100124；2.北京市水質科學與水環境恢復工程重點實驗室，北京 100124；3.深圳市同濟人建筑設計有限公司，廣東深圳 518000)

目前國內海綿城市建設處于起步階段，技術研究尚相對薄弱；對于海綿城市建設中涉及的低影響開發技術措施(LID)的不同組合研究更少。對于規劃設計過程中選用的不同LID組合措施急需建議一套統一、有效的評估方法，以提高LID措施的組合設計的科學性、有效性、合理性及經濟性。LID措施的組合優化評估是一個復雜、多因素與多層次的系統。層次分析法(analytic hierarchy process，AHP)是一種將定量與定性相結合的系統化結構化的評估決策方法[1]，其主要適用于多目標因素結構復雜、缺乏必要數據和需要將經驗判斷定量化的情況。其缺點是構造模糊判斷矩陣時沒有考慮到人的判斷模糊性，而且一致性檢驗過于復雜[2]。三角模糊數層次分析法(triangular fuzzy number-analytic hierarchy process，TFN-AHP)彌補了AHP法的不足之處，可以保證評估決策結果的客觀性[3-4]。目前在結合LID措施評估決策上的相關應用研究都只是停留在單項措施選用方面：如Young等[5]和謝季堅等[6]在2010年運用AHP對不同雨洪管理措施進行了決策分析；謝玉霞[4]在2013年運用模糊層次分析法在雨洪管理措施決策進行分析研究。

本研究通過利用TFN-AHP方法對LID幾項單項技術措施的不同組合優化方案以定性和定量相結合的方式進行了評估研究，從海綿城市建設方案實施的角度，提供了一套科學、合理、可操作性的評估方法。

1 LID組合優化措施評估指標體系

1.1 單項LID措施評估比選體系

選用不同單項LID措施在技術性(A1)、經濟性(A2)與社會效益(A3)指標方面展開分析。技術性指標(A1)由徑流量削減率(B1)、雨峰流量削減率(B2)和徑流污染削減率(B3)三項來構建。經濟性指標(A2)由基建成本(B4)、運行維護成本(B5)兩個來表示；社會效益指標(A3)主要包括景觀效應(B6)和生態功能(B7)。研究選用的單項LID措施有綠色屋頂(O1)、透水鋪裝(O2)、下凹式綠地(O3)和雨水調蓄池(O4)等四種。

根據深圳市、武漢市和上海市等省市海綿城市建設技術導則以及相關研究的相關數據統計分析，建立單項措施比選框架圖(圖1)和單項海綿城市LID措施指標比選表(表1)。

圖1 單項海綿城市LID措施比選框架圖Fig.1 Comparison and Selection of LID Measures for Individual Item of Sponge City

指標措施徑流量削減率雨峰流量削減率徑流污染削減率(以SS計)基建成本運行和維護成本景觀效益生態功能綠色屋頂25%～70%☆☆70%～80%☆☆☆☆☆☆☆☆☆☆☆透水鋪裝30%～75%☆☆80%～90%☆☆☆☆☆下凹式綠地20%～32%☆50%～75%☆☆☆☆☆☆☆☆雨水調蓄池50%～80%☆☆☆30%～50%☆☆☆☆☆地下沒有影響,地上影響很小☆

注：無-無效果； ☆-效果差； ☆☆-效果中等； ☆☆☆-效果很好

1.2 LID組合優化措施評估指標體系

將單項LID措施進行組合，形成不同的方案。研究中以上述4種措施構建形成了11種不同組合方案，用字母加數字的方式來命名每一種方案，如圖2所示。

之后進行LID措施組合方案遞階層次分析體系的構建。該階層次分析體系為四層，包括目標層、準則層、指標層以及方案層。

圖2 海綿城市LID措施組合方案遞階層次分析體系Fig.2 Hierarchical Analysis System of LID Measures Combination Scheme for Sponge City

2 三角模糊綜合評估模型

2.1 三角模糊數基本概念

(1)

圖3 三角模糊隸屬度函數Fig.3 Triangular Fuzzy Membership Function

(2)

(3)

(4)

2.2 構造模糊判斷矩陣

表2 1～9標度法及其含義Tab.2 1～9 Scale Method and the Meanings

在三角模糊數構造的模糊判斷矩陣[n,m,u]中，中間值m為專家給出的兩指標相對重要程度，模糊評判區間下界n和上界u可根據專家對判斷模糊程度確定；u-n越大，表示專家的判斷越模糊；u-n越小，表示專家越清楚。

2.3 計算評估指標的權重

(1) 利用判斷矩陣構造模糊評價因子矩陣E，計算方法如式(5)。

E=(eij)n×n=

(5)

(2) 計算調整判斷矩陣Q，如式(6)。

(6)

其中，矩陣M為判斷矩陣中所有三角模糊中間值mij組成的矩陣。

(3) 將調整判斷矩陣Q按列轉換成對角線為1的判斷矩陣，記為判斷矩陣P，如式(7)。

Pij=(pij)n×n

(7)

且滿足式(8)。

(8)

(4) 利用相容矩陣分析法對矩陣P進行變換，得到相容矩陣R，如式(9)～式(10)。

R=(rij)n×n

(9)

rij=rikrkj(k=1,2,…,n)

(10)

且滿足式(11)。

(11)

同時滿足式(12)。

(12)

(5) 計算在標準層中各指標分別在方案層中的權重ωα-Si，如式(13)和式(14)。

(13)

(14)

2.4 計算各指標對于總目標綜合權重

計算各指標對于總目標的綜合權重ω。將計算指標層中的不同指標條件下在方案層中對應不同的權重ωα-Si，根據相同方法計算指標對應的不同權重ωa(a=1)。根據求得指標權重與指標條件下的方案權重進行綜合權重計算，如式(15)。

ω=ωaωα-Si(i=1,2,…,n)

(15)

且將其進行排序，選出最佳組合優化措施。

2.5 利用PCSWMM模型進行模擬驗證

首先由于TFN-AHP法的計算太過復雜，利用MATBAB軟件對上述TFN-AHP法的計算原理進行編程計算，可大大提高計算速度。再將原有措施方案sn(n=1,2,…,11)分別帶入PCSWMM模型中進行模擬分析驗證，將在不同指標Bt(t=1,2，...，7)條件下模擬結果排序。

其中，構建PCSWMM模型主要由降雨數據、管網數據、子匯水區以及模型其他參數等組成。

降雨數據是由研究區域的暴雨強度公式和芝加哥雨型公式進行耦合得到。

管網數據一般是由管道參數(長度、坡度、管徑等)、檢查井參數(地面標高、井底標高等)以及排放口(井底標高、是否淹沒出流、是否有潮汐等)等參數組成。

利用ArcGIS中一個創建泰森多邊形功能命令來劃分子匯水區，子匯水區數據有子匯水區編號、出水口、面積和雨量計等；用PCSWMM模塊進行地表產匯流計算時，參數包括不透水區百分比、寬度和坡度等。

根據研究區域的地形和土壤特點，查閱研究區域相關雨洪模型文獻資料以及SWMM手冊，得到PCSWMM模型的水文水力模塊主要參數初始值如表3所示。

表3 PSWMM模型水文水力模塊主要參數初始值[10-12]Tab.3 Initial Values of Main Parameters of Hydrologic and Hydraulic Module for PSWMM Model [10-12]

模擬結果根據不同LID措施組合條件下系統出流量變化曲線進行分析，其中出流量曲線峰值大小可以得到模型雨峰削減效果好壞，即用雨峰削減百分率表示；為此雨峰削減百分率大小排序與利用三角模糊層次分析法(TFN-AHP)計算的權重ωi排序相吻合，則說明該方法有效、可行的；從而根據綜合權重集合V={υ1,υ2,…,υn}(n=1,2,…,11)得到最佳LID措施組合方案。

3 實例分析

以某濱海城市填海區海綿城市建設工程中LID措施組合優化方案的選擇為研究案例，對上述LID組合措施評估方法進行驗證分析，以期為今后海綿城市LID組合措施的工程應用提供借鑒。

首先根據三角模糊綜合評價模型原理，構造不同LID組合措施的模糊判斷矩陣。其中以“B2雨峰流量削減率”為準則條件下構造的模糊判斷矩陣B=(bij)11×11(表4)。

依據三角模糊綜合評價模型計算原理，利用MATLAB軟件編程將在不同準則條件下計算在方案層中方案權重ωα-Si。在以“B2雨峰流量削減率”為準則條件計算得到ωα-Si(i=1,2,...,11)，如表5所示。在以“B2雨峰流量削減率”為準則條件下得到權重排序情況可以得知，方案S11(綠色屋頂+透水鋪裝+下凹式綠地+雨水調蓄池)在雨峰削減效果方面最好，其次是方案S8(綠色屋頂+透水鋪裝+雨水調蓄池)，排第三的是方案S10(綠色屋頂+下凹式綠地+雨水調蓄池)，相對來說雨峰流量削減效果最差是方案S4(透水鋪裝+下凹式綠地)。

表4 “B2雨峰流量削減率”為準則條件下構造的模糊判斷矩陣Tab.4 Fuzzy Judgment Matrix Constructed under Criterion Conditions of “B2 Rain Peak Flow Reduction Rate”

表5 在以“B2雨峰流量削減率”為準則條件下各方案權重值排序表Tab.5 Sorting of Weights of Schemes under the Criterion of “B2 Rain Peak Flow Reduction Rate”

根據同樣的方法及MATLAB軟件，在以各個指標為準則條件下得到各個方案權重值ωα-Si，如表6所示。

表6 各指標條件下的各方案權重值Tab.6 Weights of Schemes under Each Index Condition

表7 指標層各個權重值及其排序Tab.7 Weight Values of Indicator Layer and the Sorting

將指標層權重與各個方案權重值進行計算得到下表中的綜合權重值，并且將其進行排序，選出最佳組合優化措施，如表8所示；可以看出，最佳組合優化措施是方案S11，依次排序是S8、S10、S9、S6、S3、S5、S7、S2、S1、S4。

表8 綜合權重值排序表Tab.8 Sorting of Comprehensive Weights

以該填海區海綿城市建設地塊為研究區域，選用該區域的降雨、管網、地形、水文等數據資料，利用PCSWMM軟件建立雨洪模型，其中降雨資料利用重現期P=2，降雨歷時t=120 min的芝加哥設計降雨；根據PCSWMM模型模擬結果，得到在不同方案措施條件下的出流量變化曲線(圖4)，并且換算得到雨峰削減率(表9)。其中在沒有潮汐情況下，最佳組合措施是方案S11(綠色屋頂+透水鋪裝+下凹式綠地+雨水調蓄池)，依次排序是S10、S9、S8、S6、S3、S5、S7、S2、S4、S1。

圖4 PCSWMM模型系統出流量變化曲線Fig.4 Outflow Curve of PCSWMM Model System

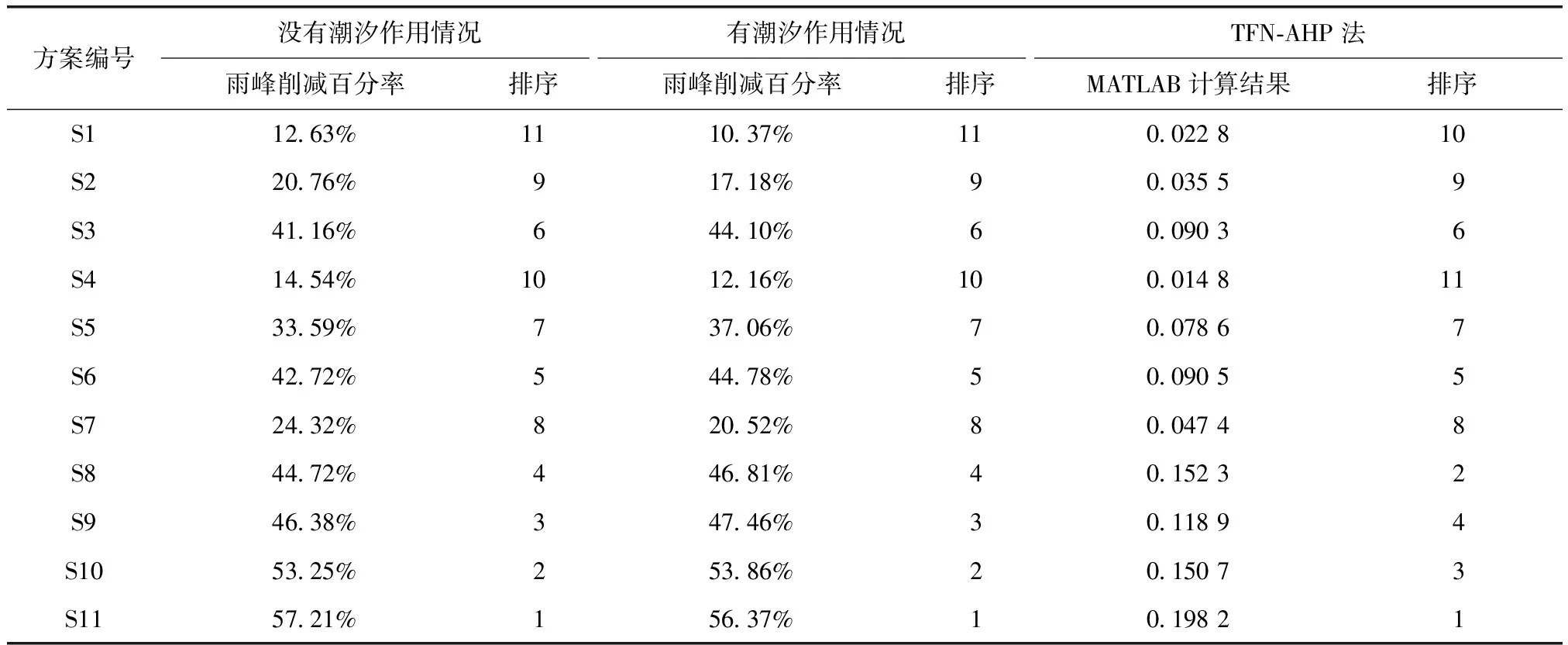
表9 在雨峰削減百分率為指標下各組合措施在TFN-AHP法與真實模擬排序對比Tab.9 Comparison of FTN-AHP and Real Simulation Sorting for Various Combination Measures under Rainstorm Reduction Percentage Index

由表9可知，TFN-AHP評估方法得到綜合權重排序情況與海綿城市PCSWMM模型模擬結果基本上是吻合的，即最佳組合措施排序依次是方案S11，S8、S10、S9、S6、S3、S5、S7、S2、S1、S4。因此，研究提出的這種基于TFN-AHP法的LID措施最佳方案評估方法是可行的。

4 結論

本研究中首先結合LID單項措施的削減效果、經濟成本、功能效益等特點構造了單項LID措施比選體系，在此基礎上建立了一套LID組合措施方案的評估指標體系。研究中結合海綿城市LID組合措施評估指標體系的特點，運用三角模糊層次分析法(TFN-AHP)建立了評估模型，有效地克服了以往評估中專家的主觀因素影響比較大的弱點，增強了科學合理性。在案例分析中，利用MATLAB軟件和PCSWMM模型輔助方案比選和計算排序保證結果可靠性和計算過程方便快捷。實例分析結果證實了該評估方法的可行性和有效性，對實際工程應用具有較好的參考價值。