初探歐拉公式

劉麗嬪

我們知道，在平面中，正多邊形都有一個對稱中心（正n邊形的中心），正多邊形也是軸對稱圖形，由此，我們說正多邊形是非常漂亮的多邊形.

讓我們再把視野放到空間中的立體圖形，將平面上的正多邊形作一推廣，即可得到正多面體的概念：如果一個多面體的各個面都是全等的正多邊形，且每個頂點處所接的面數同樣多，即為正多面體.正四面體（圖1（1））是非常優美的空間幾何體，它的每一個面都是全等的正三角形，每一個頂點在相對的平面三角形上的投影也是該正三角形的中心.

那么我們不禁會問：在平面上，只要正整數n≥3，就存在相應的正n邊形，到了空間中，是否也有類似情況存在呢？即是否有正五面體呢？正六面體？正n面體呢（其中n≥4，n∈N?）？

為了幫助大家解決上面的疑問，我們先來看這樣一個問題：多面體的頂點數、棱數和面數之間有關系嗎？

同學們可以先從下面簡單的情形開始嘗試：如圖1（1）～（3）所示的3個多面體，分別數出它們的頂點數V、面數F和棱數E，并制成表格.

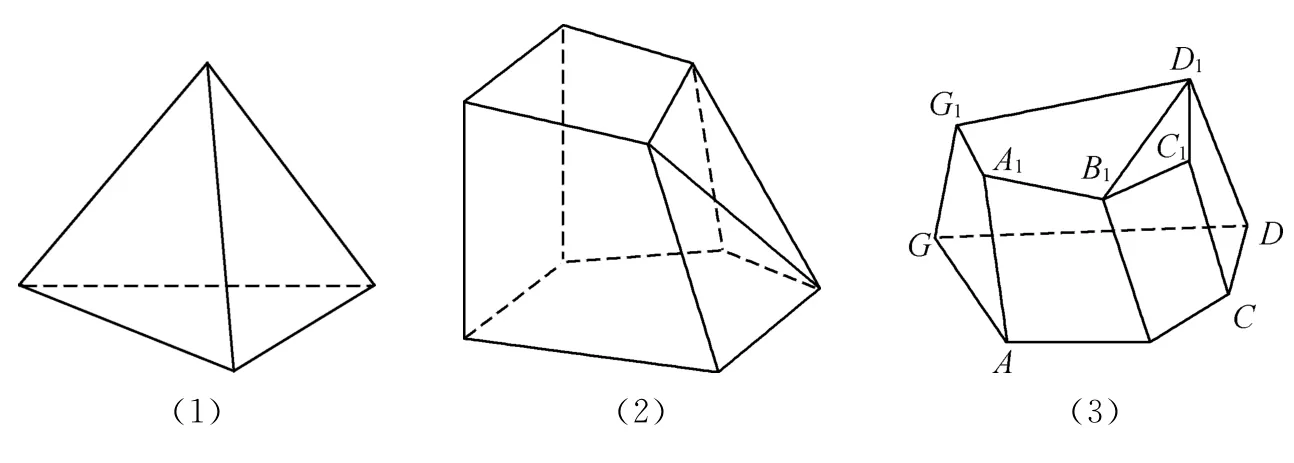
圖1

表1

我們發現，多面體的頂點數、面數、棱數滿足等式關系：V+F-E＝2. （*）

當然，并不是任意一個多面體都有這樣的規律.

我們發現如果把（1）～（3）中多面體的任何一個面延展，那么多面體一定在這個面的一側，我們把這樣的多面體稱為凸多面體.而另外的一些多面體，總存在某個面，將它延展，多面體分布在其兩側，我們把這樣的多面體叫做凹多面體.有些凹多面體就不滿足V+F-E＝2這個等式.

那么我們能不能嘗試證明（*）式呢？我們以圖1（3）為示意圖，假設該簡單多面體有F個面，且每個面的棱數分別為E1，E2，E3，…，EF，則有E1+E2+E3+…+EF＝2E（因為每條棱加了兩遍），我們計算這個簡單多面體的內角和為：（E1-2+E2-2+…+EF-2）π＝（E1+E2+…+EF）π-2Fπ＝2Eπ-2Fπ＝2π（E-F）.我們用面數和棱數表示出了簡單多面體的內角和，現在我們嘗試從另一個角度用頂點數表示內角和.我們假設這個多面體是由薄橡皮膜做成，內部是空的，有一個面破了，把其余各面攤開在一張平面圖上，如圖1（3）展成圖2，設去掉的一個面為n邊形，則得到一個n邊形的展開圖，并且內部有（V-n）個頂點.那么展開后的平面圖形的內角和為（n-2）π+（V-n）2π，再加上去掉的一個n邊形的內角和為（n-2）π，所以該簡單多面體共有內角和為（n-2）π+（V-n）2π+（n-2）π＝（V-2）2π，則2π（E-F）＝（V-2）2π，即V+F-E＝2.

這個結論是瑞士數學家歐拉在1750年發現的，也稱為歐拉公式.歐拉公式的背后是一門新的幾何學，它只研究圖形各部分位置的相對次序，而不考慮圖形的形狀和大小，如今這門學科已經發展成數學的一個重要的分支——拓撲學.

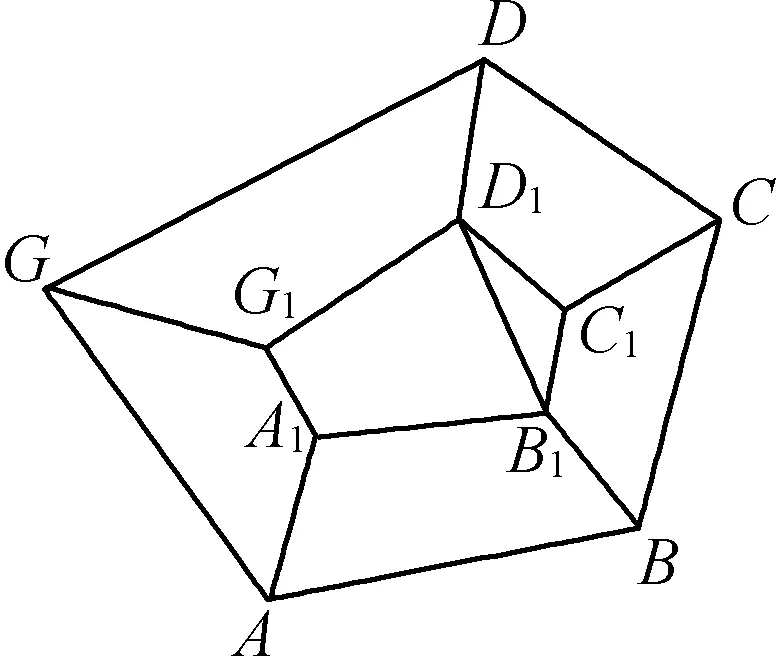
圖2

現在我們再來回答文章開頭提出的問題：如果正n面體存在，n可以取哪些值呢？我們假設正多面體頂點數V、面數F、棱數E，且每個面是正n（n≥3）邊形，每個頂點有t（t≥3）條棱.那么有n F＝2E，t V＝2E，則，代入歐拉公式V+F-E＝2，即，整理得：.因為，所以.我們知道，若n＞3，t＞3，則矛盾，因此n和t中，至少有一個為3.若n＝3，t＜6，則t＝3，4，5；若t＝3，則n＝3，4，5.綜上，只可能有五種正多面體，分別是正四面體、正六面體、正八面體、正十二面體和正二十面體.

數學中，以歐拉命名的公式還有很多，同學們可以利用課余時間進一步研究更多更美妙的歐拉公式.歐拉是一位非常值得我們尊敬的數學家，命運曾幾次向他伸出魔爪，在他28歲時，過度的工作使他的右眼失明，之后，他的左眼也完全失明.而他辛苦創作的著作又在一次火災中化為灰燼.即便命運對他如此不公，他也絲毫沒有放棄自己的鉆研.歐拉在雙眼失明的情況下，憑記憶和心算繼續研究數學，口述了多本書和400多篇論文.

歐拉用頑強的毅力，孜孜不倦的奮斗精神，推動著數學的車輪不斷前行，他對近代數學的發展產生了極其深遠的影響.以他名字命名的那些公式如此美麗，如此精妙，成為數學殿堂的一道亮麗風景線！