基于傳感器網絡的1比特RLS算法*

彭秋燕,劉兆霆,姚英彪

(杭州電子科技大學通信工程學院,杭州 310000)

由大量傳感器節點組成的無線傳感器網絡在環境監測、目標定位和跟蹤等領域具有廣泛的應用。這些應用所涉及的理論問題一般可以歸結為是從傳感器采集的測量數據中估計未知的物理量參數,并且隨著無線傳感器網絡的快速發展,該問題已經吸引了大量國內外學者的關注。通常情況下,無線傳感器網絡中每個傳感器節點由電池供電,其計算、通信和信息存儲能力有限[1],另外,網絡的通信帶寬也是一個有限的資源。這使得如何基于傳感器網絡獲得有效的參數估計,同時盡可能降低網絡的使用成本問題成為一個具有理論意義和實用價值的研究熱點。

解決此問題的其中一個研究方向是將每個傳感器節點的測量值壓縮為1比特或多比特的信息,然后利用這種壓縮后的數據,設計相應的算法實現參數估計。與未經量化的模擬測量值相比,壓縮后的1比特測量值雖然僅含有非常有限的信息量,但通常可以通過更便宜的二進制傳感器來獲取,并且能夠降低設備的存儲容量和減小網絡的通信帶寬。目前,國內外已有大量基于1比特參數估計算法的研究,例如,在被估計參數是一個標量的情況下,人們提出了許多參數化方法[2-4]和非參數化方法[5-7];在被估計參數是一個矢量的情況下,人們提出了回歸參數的1比特估計方法[8,9],1比特系統辨識方法[10,11],1比特壓縮感知算法[12-16]等。

這些現有的方法都有各自的優點,但它們一般都依賴于某些假設,如噪聲方差已知[3,4]、噪聲的累積分布函數可逆[5,11]、量化器的輸入不含噪聲[13,15,16]、未知參數的動態范圍已知[6]、模型中使用的量化器閾值為零[9,12]等。這樣的假設在許多實際情況下并非總是成立的。例如,Wigren T[14]提出了一種利用1比特測量值的歸一化隨機梯度自適應濾波方法,但是該方法假設量化器的輸入端不存在測量噪聲,在噪聲存在的情況下不能保證收斂。此外,大部分現有的算法大都是批處理方法,很少考慮基于1比特測量值的在線參數估計問題。在線處理相對于批處理方案具有更低的復雜性和存儲要求,并且能夠實現對慢變參數的估計。雖然Zayyani H等[16]將輸入矢量乘以估計矢量的符號函數與1比特測量值之間的最小均方誤差準則用于壓縮感知中1比特測量值的在線稀疏參數估計,但是該準則也不能為所得的估計性能提供強有力的理論支持。

在自適應濾波中,遞歸最小二乘RLS(Recursive Least Square)算法在收斂速度和估計精度方面均優于最小均方LMS(Least Mean Square)算法。然而,基于1比特測量值的RLS參數估計算法很少有報道。本文提出了一種基于無線傳感器網絡1比特測量值的自適應RLS參數估計算法。該算法結合了期望最大EM(Expectation Maximization)和遞歸最小二乘法,具有與經典RLS算法幾乎相同的穩態性能。

1 傳感器網絡和信號參數估計模型

假設一個由K個節點組成的傳感器網絡,每個節點能夠與一個共同的融合中心FC(Fusion Center)進行無線通信,且每個節點k在每個時刻i能夠獲得對某一感興趣信號的測量值yk,i:

(1)

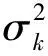
如引言所述,為了降低網絡的通信帶寬和節點的能量消耗,本文考慮每個傳感器節點不直接傳輸測量信號yk,i,而是先將其與一個門限值進行比較,然后向FC報告測量信號是大于該門限(用1表示),還是小于該門限(用-1表示),即每個節點向FC傳輸1比特數據dk,i:

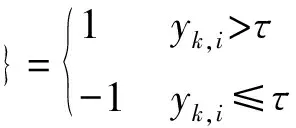
(2)

式中:τ是選定的門限值。另外,正如Chi Y等[17]以及Konar A等[18]的做法,本文進一步假設,每個傳感器節點的輸入矢量uk,i是由隨機序列發生器根據不同的隨機種子產生的,并且FC已知每個隨機種子,從而可以同步復制每個傳感器節點的輸入矢量uk,i。本文的主要目的是利用各個節點傳輸給FC的1比特數據{dk,i}來實現對未知參數w0的自適應估計。

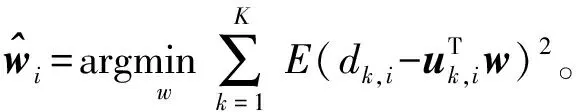
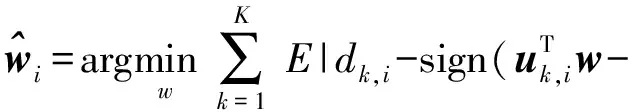
(3)

然而,當噪聲vk,i存在時,(3)不能保證參數的估計性能。因此,本文將從最大似然估計(Maximum Likelihood Estimation,MLE)原理推導一種基于期望最大和遞歸最小二乘的自適應參數估計算法。

2 最大似然估計方法

此節首先給出一種基于隨機梯度SG(Stochastic Gradient)迭代和Probit模型的最大似然估計方法,然后推導出一種基于權重的最大似然估計算法。

2.1 基于Probit模型的最大似然估計(Probit-MLE)

式(1)可以看作是dk,i條件概率的Probit回歸模型,即

式中:Φ(·)是標準正態分布的累積分布函數,且γk,i根據最大似然估計原理,可以從測量值{dk,i}中得到w0的估計值,即基于Probit模型的最大似然估計器的解為:

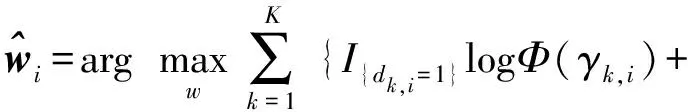
(4)

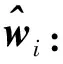
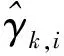
2.2 基于權重的最大似然1比特RLS算法

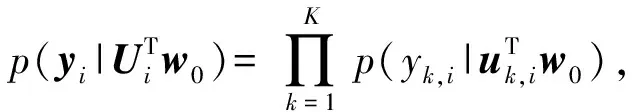
(5)

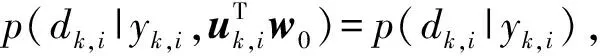
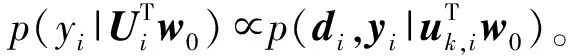
(6)

隨后把數據{yj}作為隱藏變量,并通過EM算法解決問題(P2)。

2.2.1EM算法

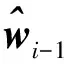
E步:

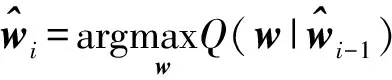
式中:Ey[·]表示對{yj}的數學期望。在E步中,利用(5)和(6)之間的等價關系,可得

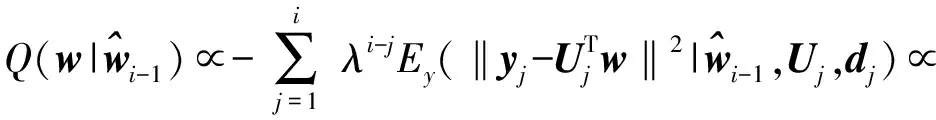
(7)

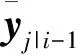
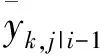
(8)

根據式(7),M步可以簡化為

(9)

式中:

Ri

(10)

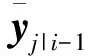
由于事件dk,j=-1和dk,j=1是互補的,且分別等效于事件yk,j≤τ和yk,j>τ,因此,從定義式(8)可以得到

引理給定一個具有標準正態分布的隨機變量v和一個常數a,v和v2的條件期望滿足:

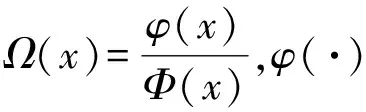
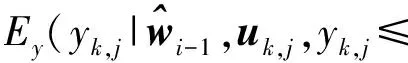
式中:γk,j|i-1同樣地,可以推出τ以上兩種情況可以統一表示為

2.2.3OB-RLS算法的總結

(11)

并結合矩陣求逆引理[22]來實現逆矩陣Pi的循環更新。然而,根據定義式(10),矢量bi不滿足類似(11)的更新規則,且隨著迭代次數i的增大,矢量bi的計算量也將越來越大。為此,可以利用近似(10)中的從而獲得這是由于與作為w0的估計值通常近似相等,并且當j接近i時,兩者相差越來越小,使得與也近似相等,并且當j接近i時,兩者相差也逐漸減小。即使當j遠小于i時,可能與有所差異,但由于權值λi-j的存在,這種差異的影響會隨著i-j的增大而減小。因此,即可得到

(12)

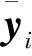
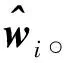
OB-RLS算法初始化:令^w0=0,P0=δIM。算法迭代:在每個時刻i,FC獲得從 K個傳感器節點發送過來的1比特數據流{dk,i},并且按照下列步驟更新參數估計值^wi:(A1)時間循環^wi=^wi-1,Pi=λ-1Pi-1(A2)節點循環for k=1,2,…,Kyk,i=uTk,i^wi-1+dk,iσkΩdk,iuTk,j^wi-1-τσk()sk,i=Piuk,i1+1KuTk,iPiuk,i^wi←^wi+1K(yk,i-uTk,i^wi)sk,iPi←Pi-1Ksk,iuTk,iPiendi=i+1,返回(A1),直至收斂。

3 性能仿真分析

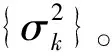
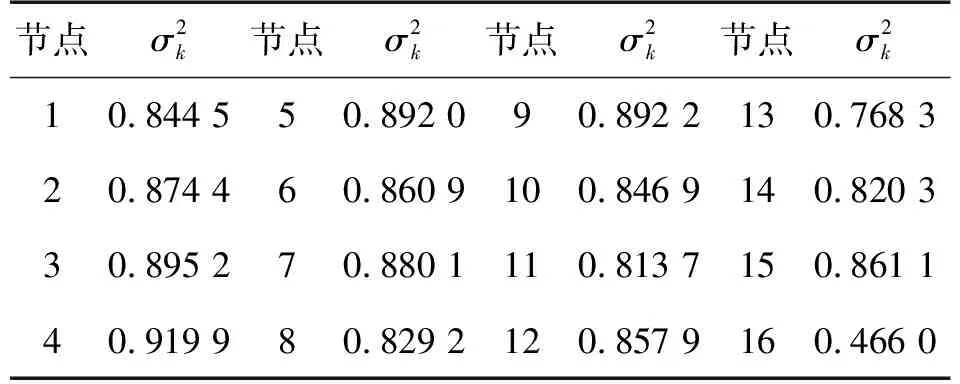
表1 所有傳感器節點的噪聲方差

圖1給出了OB-RLS算法的瞬態MSD與迭代次數i的關系,并且考慮了設置不同的閾值情況。從圖中可以觀察到,雖然OB-RLS算法僅使用了1比特量化測量值,但在穩定狀態時仍能達到和傳統RLS算法幾乎相同的估計精度。另外,從圖1中還可以看出,OB-RLS算法的收斂速度比傳統RLS算法慢,但是設置較小的閾值(絕對值)有利于提高收斂速度。

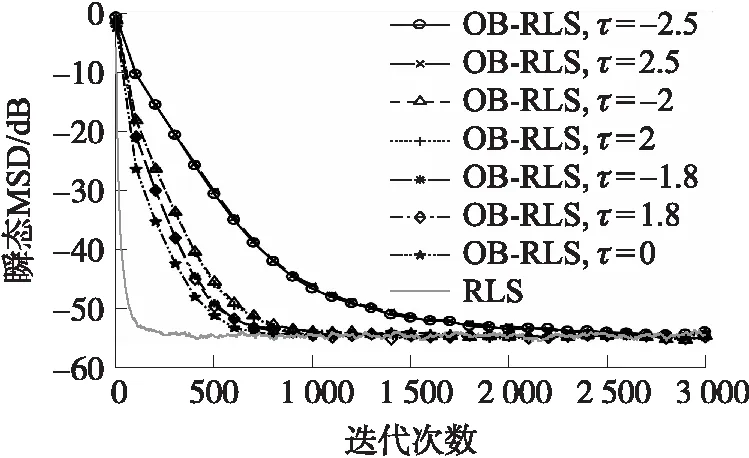
圖1 傳統RLS和OB-RLS的瞬態MSD

圖2對比了4種算法的瞬態MSD。這4種算法分別是:符號濾波算法(3)、Probit-MLE算法(4)、傳統RLS算法(使用未經量化數據yk,i)以及本文提出的OB-RLS。設置傳統RLS和OB-RLS算法的遺忘因子 λ=0.98,Probit-MLE和符號濾波算法的步長分別為0.03和0.3。從圖中可以看到,Probit-MLE算法的估計精度比符號濾波算法高,但兩者的精度都比本文所提出的OB-RLS算法低。

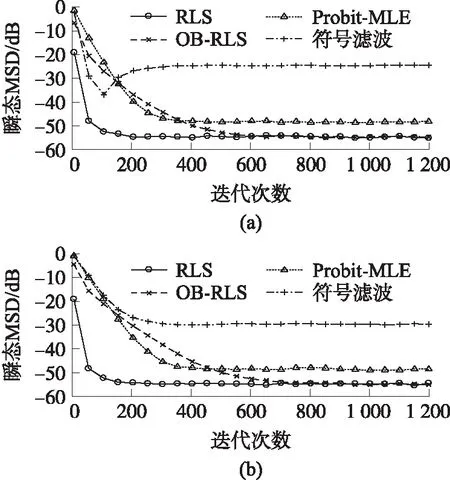
圖2 4種算法的瞬態MSD對比

圖3進一步顯示了在不同閾值下,3種算法的穩態性能。設置OB-RLS算法的遺忘因子λ=0.98,Probit-MLE和符號濾波算法的步長分別為0.03和0.3。從圖中可以觀察到,當閾值τ由-2.5增加到2.5的過程中,符號濾波算法的性能波動較大,對閾值τ比較敏感,而OB-RLS算法和Probit-MLE算法的估計性能比較穩定,并且在這個過程中,本文的OB-RLS算法始終有更低的估計誤差。

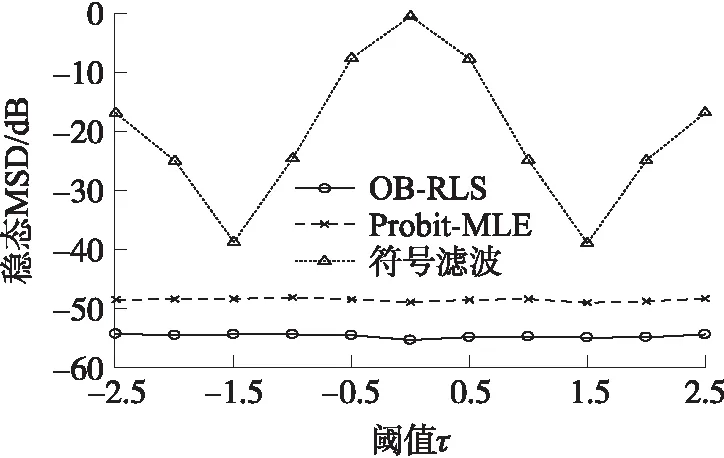
圖3 不同閾值下的穩態MSD

4 結論

本文研究了基于傳感器網絡的自適應參數估計問題,提出了一種利用傳感器節點1比特測量值的OB-RLS算法。為了降低各節點的能耗、存儲資源,以及到中心處理器的通信帶寬,首先將各節點采集的測量信號壓縮為1比特數據,然后再發送給中心處理器。在中心處理器中,采用文中所提出的OB-RLS算法來獲得對感興趣參數的自適應估計。該算法結合了期望最大化的思想和遞歸最小二乘方法,相比符號濾波算法和Probit-MLE算法有較低的估計誤差和較好的穩定性,且和傳統RLS算法估計精度相當。論文通過MATLAB仿真實驗,驗證了算法的性能。