立體幾何中探究性問題的追根溯源

■河南省商丘市第一高級中學

高考中的立體幾何探索性試題我們一般可以采用綜合推理的方法、分析法、特殊化法和向量法來解決。

探索性問題主要是對平行、垂直關系的探究,這類試題的一般設問方式是“是否存在?存在給出證明,不存在說明理由”。解決這類試題,一般根據探索性問題的設問,首先假設其存在,然后在這個假設下進行推理論證,如果通過推理得到了合乎情理的結論就肯定假設,如果得到了矛盾就否定假設。

例題如圖1,在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=2a,點E在PD上,且PE∶ED=2∶1。

(1)證明PA⊥平面ABCD。

(2)求以AC為棱,EAC與DAC為面的二面角的大小。

(3)問:在棱PC上是否存在一點F,使BF∥平面AEC?證明你的結論。

解析：(1)因為底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a,在△PAB中,由PA2+AB2=2a2=PB2,知PA⊥AB,同理PA⊥AD,所以PA⊥平面ABCD。

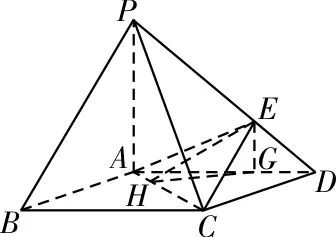
圖1

(2)作EG∥PA交AD于G,由PA⊥平面ABCD,知EG⊥平面ABCD,作GH⊥AC于H,連接EH,則EH⊥AC,則∠EHG為所求二面角的平面角,設為θ。又PE∶以θ=30°。

(3)以A為坐標原點,直線AD,AP分別為y軸,z軸,過A點垂直平面PAD的直線為x軸,建立空間直角坐標系,如圖2所示。由題設條件,相關各點的坐標分別為A(0,0,0),

圖2

解題思路：(1)證明的是線面垂直,只要努力去找直線與平面內的兩條相交直線垂直即可；(2)按找二面角的方法進行；(3)通過建立恰當的直角坐標系,給出相應點的坐標,利用坐標關系和向量的相等就可以解決了。

例題追根溯源：如圖1,在底面是菱形的四棱錐P-ABCD 中,∠ABC=60°,PA=AC=a,PB=PD=2a,點E在PD上,且PE∶ED=λ∶1(λ∈N*)。

(1)證明PA⊥平面ABCD。

(2)在棱PC上是否存在一點F,使BF∥平面AEC?證明你的結論。

解析：(1)因為底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a,在△PAB中,由PA2+AB2=2a2=PB2,知PA⊥AB,同理PA⊥AD,所以PA⊥平面ABCD。

(2)解法一:以A為坐標原點,直線AD,AP分別為y軸,z軸,過A點垂直平面PAD的直線為x軸,建立空間直角坐標系,由題設條件,相關各點的坐標分別

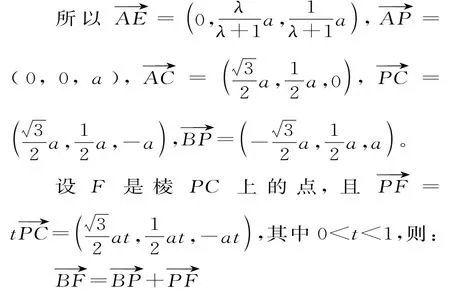
審題方法：F是段線PC上的點,一般可,求出t的值,點P是已知的,即可求出點F。

解題思路：通過建立恰當的直角坐標系,給出相應點的坐標,令所求直線對應的向量用該平面內的兩個不共線向量表示即可。

解法二:如圖3,在PE上取一點M,使得ME=ED,過 點M 作MF∥EC交PC于點F,連接BD交AC于點O,連接EO,BM。

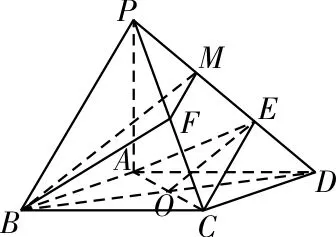
圖3

在△DBM中,E,O分別是DM,DB的中點,所以EO∥BM,即BM∥平面AEC。

審題方法：作出適當的輔助線,利用中位線定理找到平行關系。

解題思路：從E點出發,在線段PE上找到點M,使得E成為MD的中點,連接OE,構造△DBM的中位線,下面只需作MF∥EC交PC于點F,這樣點F就被找到了。