分析駕駛行為的快速路交通流元胞自動機模型

李 杰，楊曉芳，付 強 LI Jie,YANG Xiaofang,FU Qiang

（1.上海理工大學 管理學院，上海 200093；2.同濟大學 交通運輸工程學院，上海 200092）

0 引言

進入21世紀，中國城鎮化、機動化進程不斷加快。全國汽車保有量持續增長，城市交通快速發展與城市規劃之間的矛盾逐漸顯露，以交通擁堵為代表的城市交通問題開始成為困擾中國大城市的普遍難題。在增加道路與基礎設施建設已經無法滿足交通需求的情況下，分析駕駛者的自身特性可以更好地提高交通出行效率。從20世紀90年代起，人們將物理學中的元胞自動機模型運用到交通領域。元胞自動機模型簡單，易于在計算機上操作；車輛按照研究者制定的運動規則和交通規則進行運動，這些規則容易更改，能實現真實生活中復雜的交通現象，獲得平均速度、流量、密度、車頭時距等參數[1]，反應交通流特性。借助元胞自動機模型的優點來分析駕駛者的特性對交通流產生怎么樣的影響。最原始的元胞自動機交通流模型則是Wolfram[2]所命名的184號元胞自動機。作為對184號模型的推廣與規則的修正Negal等人1992年首次提出簡單的CA模型來研究單車道的交通行為，即著名的NaSch模型[3]。隨后，在NaSch模型的基礎上，研究者們又提出了很多模型[1,4]。

在基礎的元胞自動機模型上，更多的人開始將駕駛者的特性加入模型中，以便找出特性對交通環境的影響。王波等研究跟車距離差異，引入期望及參照點理論，提出期望安全車距（ESD）概念[5]。徐程等為了描述真實交通環境中車輛交錯跟馳的現象，在全速度差模型的基礎上引入了視覺角和側向偏移角的概念[6]。黨睿娜等分析駕駛員接近前車行為決策的基礎上，研究了換道階段的車輛、車間狀態變化和換道操作習慣等[7]。徐學珍通過車載高精度實測數據，分析得出車輛在不同的行駛狀態確定相應的駕駛員反應時間，得出相應狀態下反應時間的分布規律[8]。唐陽山、夏道華認為駕駛員的反應時間會影響汽車的制動距離，從而影響駕駛員在緊急情況下通過制動來避免碰撞的安全距離[9]。確定性減速過程計算類似于碰撞安全距離計算，受到反應時間的影響。大多數研究者對駕駛者特性的研究都是在影響因素的評價以及反應時間給行車帶來的安全的宏觀研究，缺少對駕駛特性在微觀交通流影響的研究。

本文針對上述NaSch模型研究的不足，提出了分析駕駛特性的快速路雙向四車道交通流元胞自動機模型。該模型增加了在變換車道和減速時駕駛者的反應時間、跟車心理、車道偏好的特性對交通流產生的影響，通過計算機在MATLAB環境下進行數值模擬，分別得到幾種條件下流量、密度、速度的關系，結合實際情況分析反應時間、跟車心理、車道偏好對交通流的影響。從最基礎的NaSch模型加以改進。

1 駕駛特性分析

目前就國內情況而言，同向行駛的汽車大多數都是處在一個完全跟車的狀態，無論前車是加速還是減速，后車駕駛者根據自己的車速判斷是減速跟馳還是變換車道，以尋求更合理的行駛狀態。

駕駛者是一個有自主意識的個體，每個個體都存在差異，即在駕駛過程中都有各自的偏好。在正常的行駛過程中，外側車道行駛車輛在內側車道滿足換道條件下，大多數駕駛者會立刻換至內側車道繼續行駛；內側車道行駛車輛在外側車道滿足換道條件下，駕駛者會綜合考慮本車道的減速行駛和外側車道的延誤行駛，根據需求機制最終做出換道選擇。但是駕駛者的特性不單單表現于此，根據駕駛經驗的豐富程度，每個駕駛者做出的判斷也會存在差別。內側車道相比于外側車道速度要更快，初學者會更偏向于外側車道行駛，經驗豐富的駕駛者則相反。

在將單車道模型推廣到雙車道時需相應的考慮車輛變換車道的要求，這時駕駛者的偏好就體現在變換車道的時機選擇和判斷。正常制定變換車道規則時，多數采用的貪婪機制和強制換道規則，而這分別適合經驗豐富的駕駛者和初學者。本文中，在臨界換道概率下增加一個偏好換道概率Pa，對于現實道路情況更加合理。

另一方面，對于確定性減速規則，現實跟車駕駛過程中，后方車輛會根據前方車輛的速度判斷自己是減速跟馳還是保持車速跟馳，在NaSch模型中確定性減速規則是在不能滿足車速的要求，那么后方車輛就立刻減速至安全距離所滿足的車速。然而在實際行車過程中駕駛者在跟車行駛時會綜合考慮前車的速度決定是減速跟馳還是保持車速跟馳，對于冒險型駕駛員偏向于考慮前車速度是否較大，則保持原車速跟馳；相對于保守的駕駛者來說，與前車距離小于安全距離就會采取減速措施。對于這種駕駛心理，本文引入一個心理參數β來描述駕駛者的冒險程度，β∈［0,1］。參數β越大說明駕駛者喜歡近距離跟車，反之則代表駕駛者跟車距離相對較大。

在實際情況中，駕駛者在做出減速跟馳和換道行為前都需要觀察周圍行車環境、獲取信息、分析、判斷、執行，這一系列的生理行為所產生的時間稱為駕駛者反應時間。駕駛的環境復雜程度、駕齡、年齡、心理生理狀態、個性、車輛速度對駕駛者反應時間的長短有重要影響。彭翹楚等對事故多發駕駛者與安全駕駛者的反應時間進行了比較研究[10]。如表1所示：

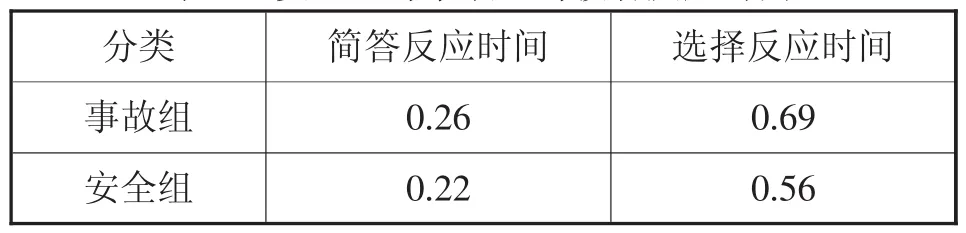
表1 安全組與事故組駕駛者反應時間

本文引入參數τ的大小代表駕駛者反應快慢，τ∈［0,1］，在突發情況或者選擇是否換道的時候反應越快越安全，換道的機會也越多。在前人的研究中都忽略了反應時間對換道時機的選擇和跟馳與否都有重要的影響。

2 模型的建立

本模型將道路視為兩條并列的、長度為L的一維離散格點鏈，每一個格點即為一個元胞，取7.5m長，元胞在任一時刻的狀態為空或者被車輛占據。假定道路上行駛的均為小汽車，第n輛車在t時刻的狀態由其速度Vn（t）表示且為離散值，Vn（t）∈［0,Vmax］，其中Vmax為車輛的最大行駛速度，Vmax=5。本文中所有車輛運動方向一致，模型采用周期性邊界條件。著名的NaSch模型是從最初的元胞自動機模型Wolfram的184號規則推廣加入慢化概率和最大車速不再是1。車輛采用4步并行更新規則：（1） 加速（2） 減速（3） 隨機慢化，以概率（4） 位置更新

NaSch模型雖然具有十分簡單的形式，但卻可以描述一些實際交通現象。比如NaSch模型可以模擬出自發產生的堵塞現象以及擁擠交通情況下的時走時停波等。

2.1 確定性減速規則。如果車道i上第n輛車在t時刻的速度（t）與反應時間行駛距離（t）大于兩車距離（t）與前車估計車速（t）之和，則強制進行確定性減速，即當：

則設定：

式（1） 中：i為車道編號（i=1,2），（t）為車道i上第n輛車在t時刻的速度（m/s）；（t）為第n輛車在反應時間內車輛行駛的距離（m）；（t）為車道i上n輛車在t時刻與前車（第n+1輛車） 的距離（m）；（t）為緊鄰前車的速度（m/s）。式（3） 中：（t）為車道i上第n輛車在t時刻的位置；（t）為車道i上第n+1輛車在t時刻的位置；ln+1為車道i上第n+1輛車的長度。易知，當β=0且τ=0時上述規則即為經典NaSch模型中的確定性減速規則。正常駕駛者反應時間參數τ是不為0/1的值，對應駕駛者不需要反應時間和不作出反應是不符合實際情況，參數τ的大小取決于駕駛者的經驗豐富程度，經驗越是豐富者越小，反之則越大。跟車心理參數β則是反映駕駛者的冒險程度，β=0/1的情況是不合理的，β=0意味著駕駛者發現與前車的跟馳距離達到臨界距離立刻減速至（t）（t）這樣會容易造成后車反應不及時而追尾；β=1意味著駕駛者覺得與前車快要產生碰撞才會采取制動措施，否則會原速行駛。

2.2 換道規則。車輛的換道規則主要考慮安全性、可移動性、交通法規和旅行時間最短原則，同時考慮了駕駛員在不同車道行駛時的換道心理，對現有的換道規則做出了改進。并且第n輛車的選擇換道概率小于臨界換道概率，則第n輛車換道必須滿足：

式（4） 中：（t）為車道i上第n輛車在t時刻與相鄰車道前方緊鄰車輛間的距離（m）；（t）為其相鄰車道前方緊鄰車輛的速度（m/s）；Pa為第n輛車的選擇換道概率；Pc為臨界換道概率。式（5） 中：（t）為車道i上第n輛車在t時刻的相鄰車道前方緊鄰車輛的位置；為相鄰車道前方緊鄰車輛的長度。

其換道規則為：

式（6）中：X3-i（t+1）為在相鄰車道下一時刻車輛的位置；V3-i（t+1）為相鄰車道下一時刻車輛的速度。

2.3 車輛狀態演化。綜合以上對于NaSch模型的改進，下面給出考慮駕駛反應時間的快速路雙車道交通流元胞自動機模型在換道、加速、隨機減速、確定性減速以及位置更新過程中的車輛狀態演化。

（1）換道過程。對于行駛在車道i上的第n輛車，若其狀態滿足下列條件：

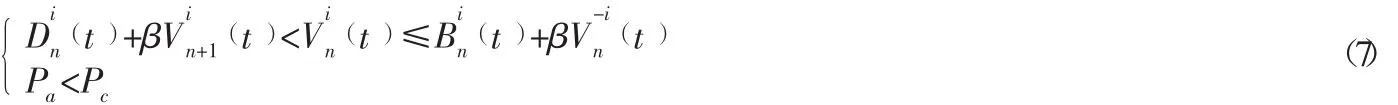
第n輛車將從車道i換道至另一車道。此時其狀態演化可表示為：

（2）加速過程。車輛在加速過程的狀態演化可表示為：

（3）隨機減速過程。第n輛車在t+1時刻會以一定的概率Pd隨機減速。其狀態演化可表示為：

（4）確定性減速過程。若第n輛車的速度滿足：

則需要進行確定性減速。此時其狀態演化可表示為：

（5）位置更新過程。在上述所有步驟都完成后，按照下式更新第n輛車在t+1時刻的位置：

在加入跟車心理、反應時間、換道選擇因素下，相較于NaSch模型更細致地解釋了交通系統的內在因素如何影響交通流，真正做到了與實際行車相符合。

3 數值模擬結果及討論

采用周期性邊界條件進行數值模擬分析，取道路長度為7.5km，每個元胞長度為7.5m，正好將道路長度組成1 000個元胞的格點鏈，假設道路車輛的總數為N。車輛的最大速度為Vmax=5。系統模擬的初始時刻，車輛的密度、位置、速度都是隨機分布在格點上，車輛的密度ρ、平均速度和平均車流量j計算公式如下：

車輛密度：

車輛平均速度：

平均車流量：

為消除模擬系統中的暫態影響，將每次系統運行的前20 000步舍去，取后10 000步，算出車輛的平均速度。本文重在考慮參數β、反應時間參數τ、偏好換道概率Pa在取不同值時交通流在雙車道運行情況。

圖1所示為在其它參數一定條件下，心理參數β取不同值時對應的流量與密度的關系。從圖中可以看出整個模擬環境中縱向的差值很大，即在不同密度下流量的變化差距很明顯，當密度較小時，道路上的車輛數隨之也就較少，車輛間距較大，不需要做出換道或者減速行為，基本保持限制速度行駛，在這種狀態下可稱之為自由流，此時駕駛者對前車的速度估計也就不存在，此時參數β對車流影響可以忽略不計。隨著密度的增加，散點圖的上升趨勢越明顯，隨之不同參數下的流量也出現了偏差，當密度增大時車輛間的相互影響開始顯現，車流的平均速度降低，部分偏好冒險的駕駛者會尋求機會換道以獲得更大的速度，此時駕駛者對前車的速度判斷顯得尤為重要，可能決定是否減速或者換道。密度處在 （0.2≤D≤0.4）范圍時，車輛的換道頻率明顯增加，駕駛者之間出現競爭行為，促使車流平均速度增大，流量增速相對低密度時加快，在適當密度下流量達到峰值。接下來密度再增大的情況下，流量反而降低，道路上的車流已經處在飽和的狀態，車輛間距減小，換道機會減少，減速概率增大，導致整個車流的平均速度降低，駕駛者不得不遵循行駛規則，所有駕駛者的行駛狀態相似，個性化概率較低，參數β對車流的影響減小，最后所有散點趨于分布在一條線上。從圖上可以看出，密度在 （0.2≤D≤0.5）時，參數β對換道影響顯著，取值越大，對應在范圍內流量越大，對換道影響越大，冒險程度越高，換道的機會越多，但是在實際行車過車中參數取值不應太大，給道路安全帶來風險。

圖2所示為在其它參數一定條件下，反應時間參數τ取不同值時對應的流量與密度的關系。從圖2中可以看出，散點分布與圖1類似，從公式中可以看出，兩個參數影響時段都是在減速和換道是產生的。密度在較低時，車道上車流處于自由流，正常限速行駛，減速概率很低，反應時間參數影響可以忽略不計，散點分布相對均勻處在一條線上，總體趨勢是流量隨密度的增大而增大。但是隨著密度的增大車道上車輛的增多，車輛間相互影響也逐漸突出，部分保守型的駕駛者可能按照正常行駛，激進型的駕駛者不會安于現狀積極尋求換道機會以獲得更大的速度，車輛的減速概率增加，密度的持續增大，使得道路上車輛趨于飽和狀態，也同時導致車輛間距進一步被壓縮，不滿足換道的條件，車輛減速跟隨成主要行車方式。區別于心理參數在于此時參數τ依然對車輛行駛有影響。總的來說反應參數對流量的影響是參數τ取值越大，流量越大，與心理參數β剛好相反。反應時間參數取值越小代表駕駛者反應速度越快，駕駛環境越安全。

圖1 Pc=0.8，τ=0.4時，流量與密度的關系

圖2 Pc=0.8，β=0.4時，流量與密度的關系

圖3 所示為反應時間參數τ=0.2、心理參數β=0.4、車流密度D=0.6的條件下，速度v和速度的方差S與反應時間參數τ的關系。從圖3中可以看出，在反應時間參數τ增大的前提下，速度總體趨勢處于降低并在一定范圍內上下浮動，相同方差也有減小的趨勢。反應時間參數總體來說對車輛行駛的速度存在一定影響。駕駛者反應時間越短，對于車輛的減速概率降低，換道的頻率加快，所以無論對于駕駛者還是管理者來說都希望駕駛者的反應時間越短也好，駕駛者可以獲得更快的速度，管理者也能提升駕駛環境的安全性。從方差來看，在參數τ較小時方差較大，此時反應時間參數較小，駕駛者的反應時間處在最佳狀態，冒險型的駕駛者會通過不斷地換道以尋求更快的速度，而保守型的駕駛者則保持一定的速度繼續行駛，導致兩者的速度差較大。在反應時間參數較大時，駕駛者的反應時間較長，方差也隨之變小。

圖4所示為反應時間參數τ=0.2、心理參數β=0.4的條件下，不同偏好換道概率下Pa的密度D與每輛車的平均換道次數的關系。從圖4可得出，在密度一定時，偏好換道概率越大車輛的平均換道次數越頻繁。可以理解為駕駛者所行駛的車道不是自己理想車道的情況下更喜歡通過換道的方式追求心理的平衡。在密度處于中間段時，道路上的車輛增加，車輛的換道需求更加迫切，導致平均換道次數急劇變化；密度較小時車輛都在自己理想的車道勻速行駛，換道需求很低，增長較為緩慢；密度較大時，道路車輛之間間距減小，換道需求正常情況下應該更為迫切，但是換道機會的減少導致了換道次數的下降。

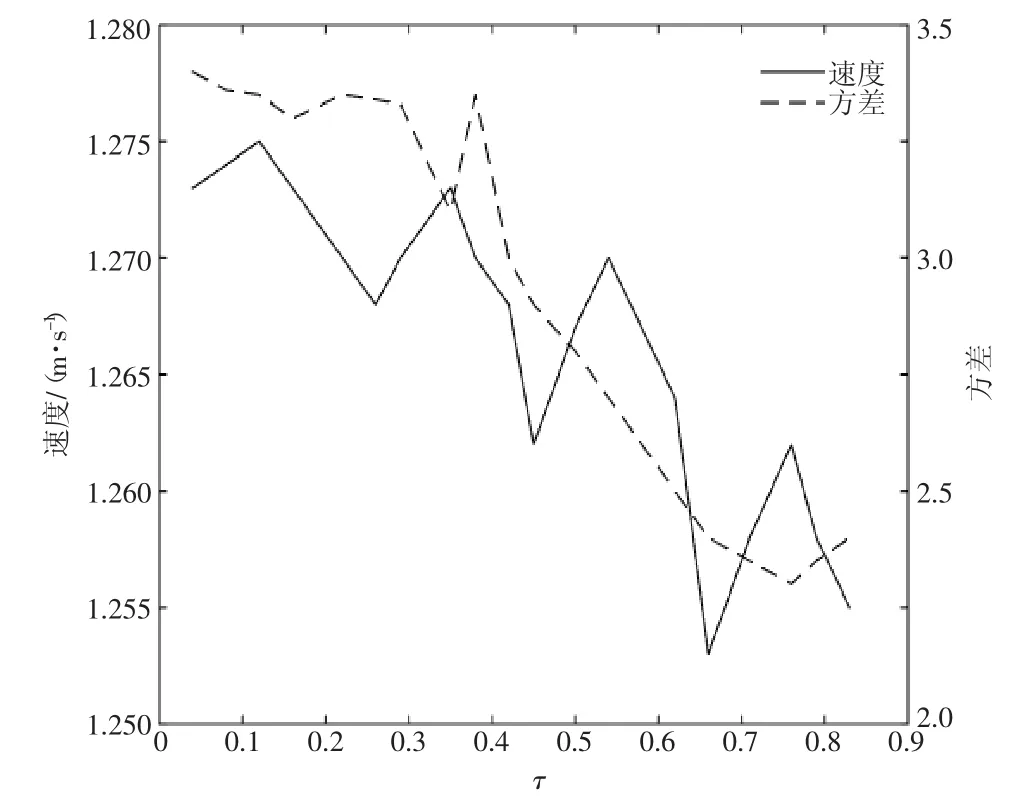
圖 3 Pc=0.8，β=0.4，D=0.6 時，速度和方差與反應時間參數τ的關系

圖 4 Pc=0.8，β=0，D=0 時，密度與平均換道次數的關系

4 結論

本文分析了常規交通流中駕駛者的自身特征和駕駛者對交通流的影響因素。在車輛行駛過程中，駕駛者的跟車心理、換道或減速行為的反應時間、車道偏好等都會對交通流產生重要影響。基于NaSch模型，構建了分析駕駛行為的雙向四車道交通流元胞自動機模型。該模型主要從駕駛者的自身因素和減速換道的硬性條件兩方面。對模型就行數值模擬，獲得不同跟車心理和反應時間參數下流量與密度的關系圖，不同換道偏好下換道次數與密度的關系圖。直觀的可以看出跟車心理、反應時間、換道偏好對于整個交通系統的影響較為明顯。在密度小于0.2時，道路上車輛較少處于自由流狀態，密度大于0.5時，道路上車輛較多速度降低，換道機會減少，駕駛者的行為特征對交通流的影響較弱。在密度處于0.2～0.5之間時，反應時間越短換道頻率越高；同樣跟車距離越近換道頻率越高，駕駛速度越快，整個交通系統的平均速度越大，隨之交通流量增大。另外，反應時間越短也代表交通環境越安全。所以我們需要提高駕駛者的反應速度來提升交通系統的安全性。本文建立的元胞自動機模型更為貼切的模擬現實交通環境，但是對參數的標定研究還不夠深入，下一步將對參數進行細致的探討。