不同風速風向條件下的列車風特性
韓運動,陳大偉,劉韶慶,林 鵬
(中車青島四方機車車輛股份有限公司 國家高速動車組總成工程技術研究中心,山東 青島 266111)
近年來,隨著高速鐵路技術的不斷發展,列車運行時速呈現逐步上升的趨勢。與此同時,列車高速運行帶來氣動效應方面的危害也日益顯著。當列車高速運行時,尤其是當列車運行與不利的環境因素(例如橫風環境)耦合時,列車風以及瞬態的壓力波動作用在鐵路沿線的人員以及設施上,會對鐵路安全造成巨大的隱患。因此,有必要對列車在不同橫風環境下運行時周圍流場的結構特征進行系統性的研究。
針對列車在橫風條件下運行時的氣動性能,已有相當數量的研究:苗秀娟[1]使用數值仿真的手段,對不同地面條件以及風向角下列車的氣動力系數進行研究,并得到列車的氣動力系數隨風向角的變化規律;田紅旗[2]通過風洞試驗的手段,研究不同風向角下列車的氣動阻力及其變化規律;于夢閣[3]通過數值仿真以及多體動力學分析方法,研究不同路況以及橫風條件下列車的脫軌系數、輪重減載率等動力學安全性指標;毛軍[4]采用數值模擬以及量綱分析的研究方法,提出列車氣動阻力系數與風速、風向角和列車車速之間關系的綜合表達式;張亮[5]通過分離渦模擬,得到列車在橫風作用下氣動載荷的非定常特性,并以動力學指標分析了列車橫風環境下運行的安全性。在這些現有研究中,均以列車受到的氣動載荷為最主要的考察對象,而針對列車運行過程中在不同風向條件下車身周圍空間以及地表的壓力、風速分布狀況即列車風特性的研究則鮮有涉及。
本文主要通過數值模擬的手段,研究列車處于不同橫風風速以及風向角下近地表以及車身周圍空間的流場分布規律,以便為高速列車風致安全性的評估提供指導。
1 數值計算方法
1.1 計算域、邊界條件設置
為減少計算量,仿真計算時列車采用2+2重聯編組,忽略受電弓等細微結構,采用簡化的轉向架結構,這一處理不僅使得列車周圍的流場不會受到太大的影響,而且易于網格的劃分,有利于數值計算的收斂。列車計算模型如圖1所示。
計算時使用的計算域如圖2所示。圖2中,計算外場的長寬高分別為400,40和30 m,保留了軌道結構的地面設施。穩態計算時,采用相對風速法給定邊界條件模擬列車與氣流之間的相對運動,即在列車運行前方邊界給定與車速方向相反的風速,計算中給定列車運行的速度為300 km·h-1,因此給定列車前方邊界均勻的風速為83.33 m·s-1。同時,為了模擬列車與地面之間的相對運動,地面給定滑移壁面邊界條件,地面滑移速度的大小和方向與前方風速的入口邊界一致[6]。在有橫風的工況中,通過計算域側面速度的入口邊界給定橫風的風速。列車的后方以及背風側則采用壓力出口的邊界條件,頂部設置為對稱邊界。
圖1 列車計算模型(2+2重聯編組)
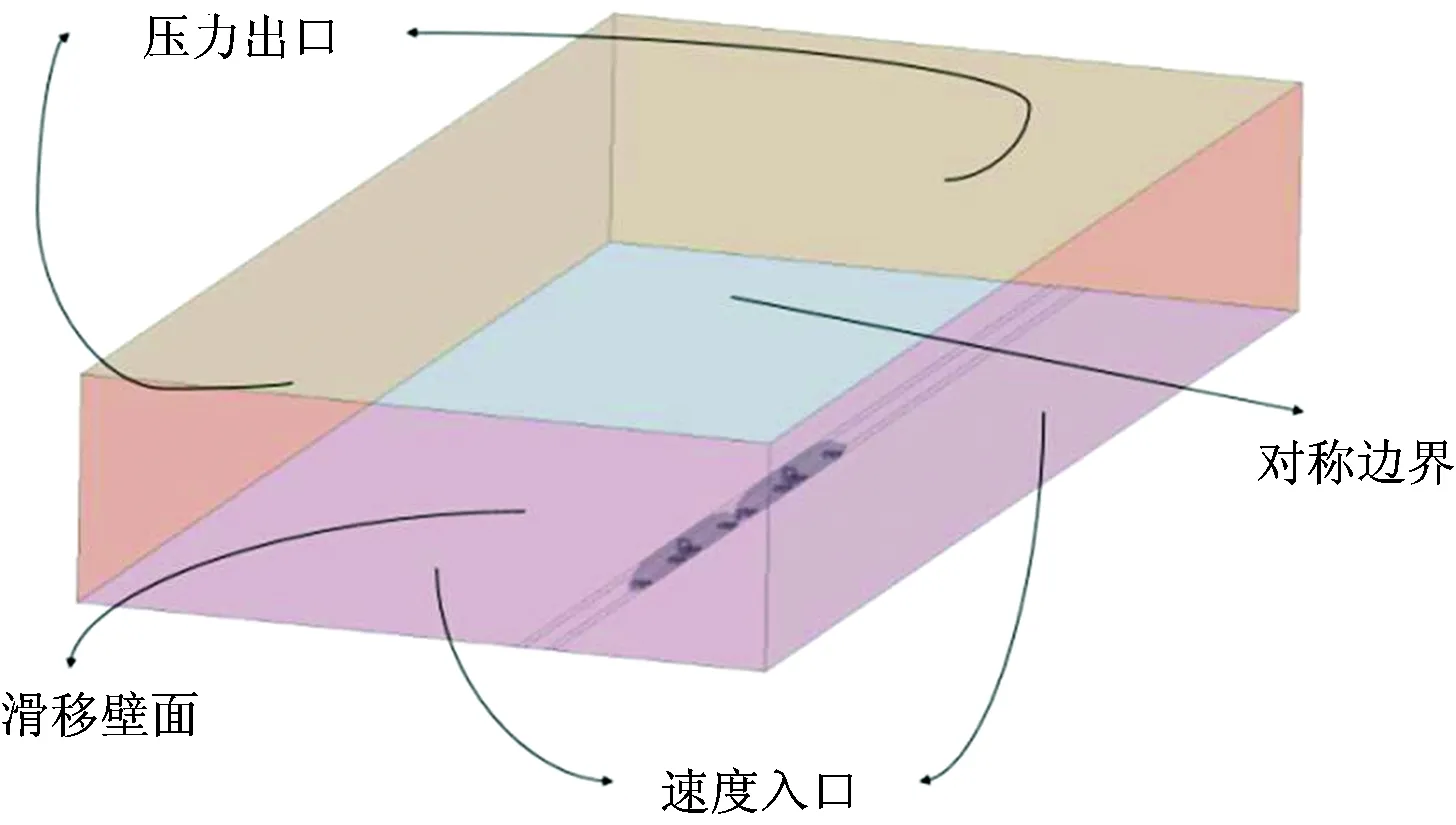
圖2 計算域示意圖
1.2 網格劃分
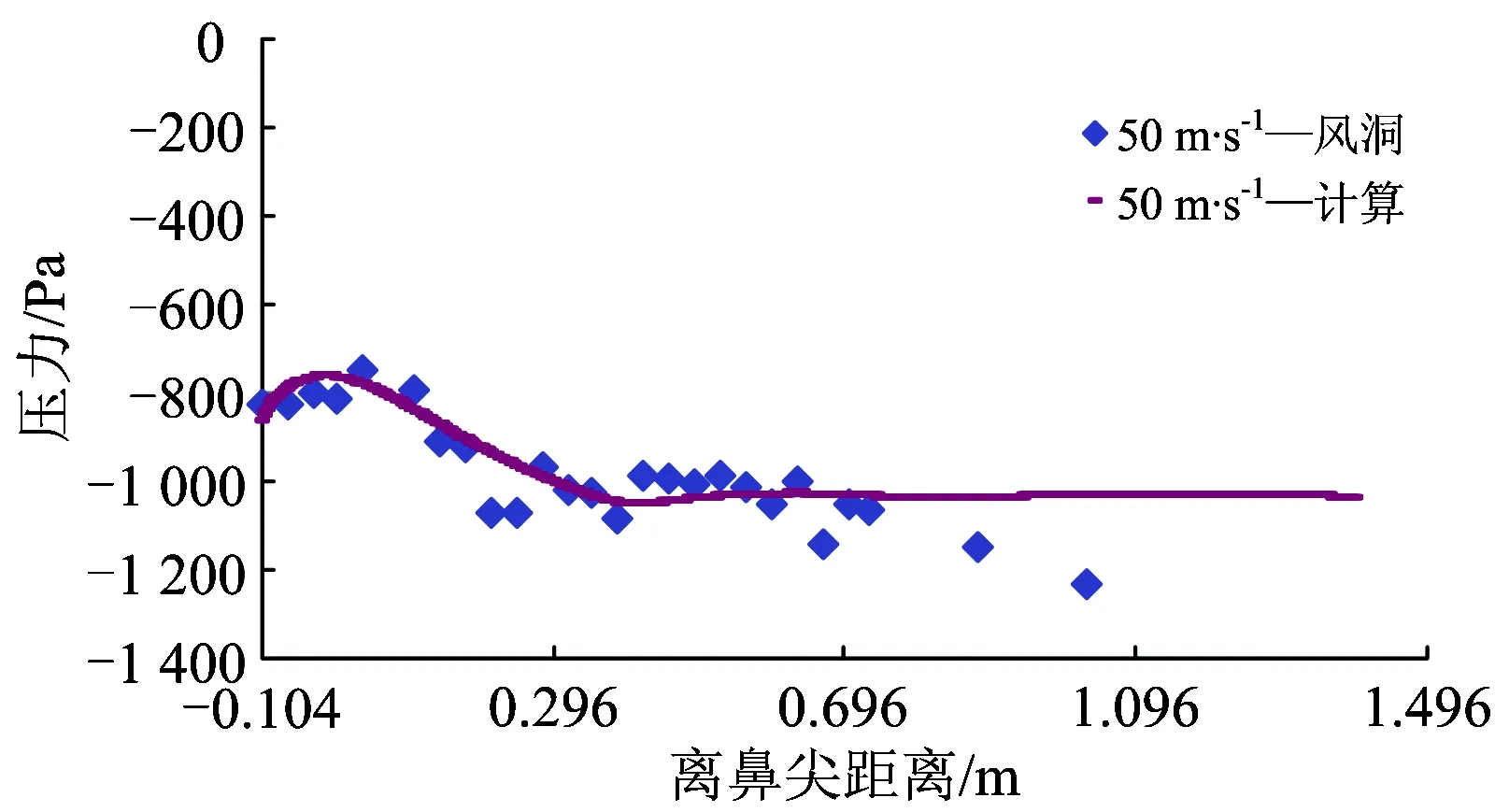
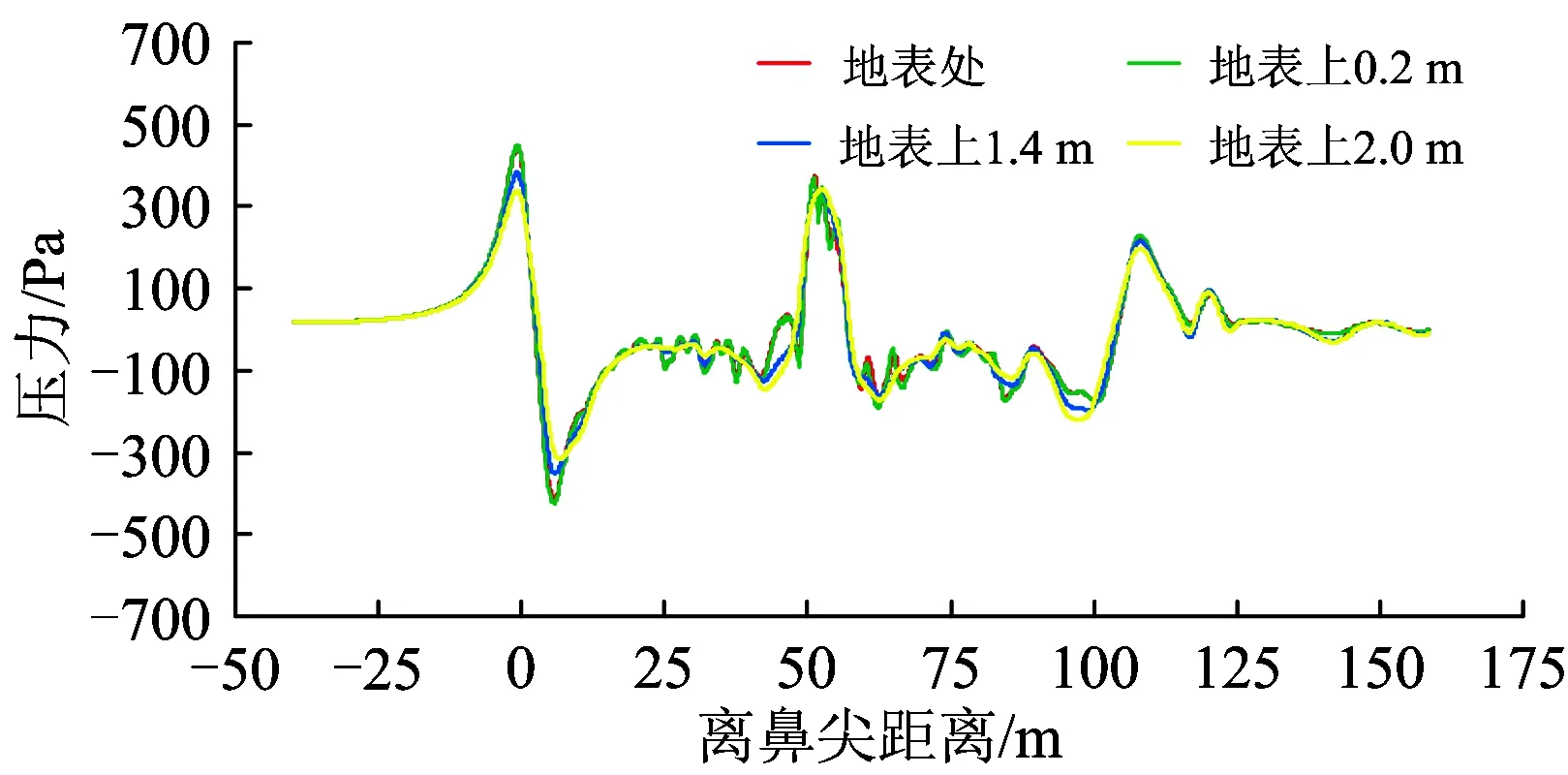
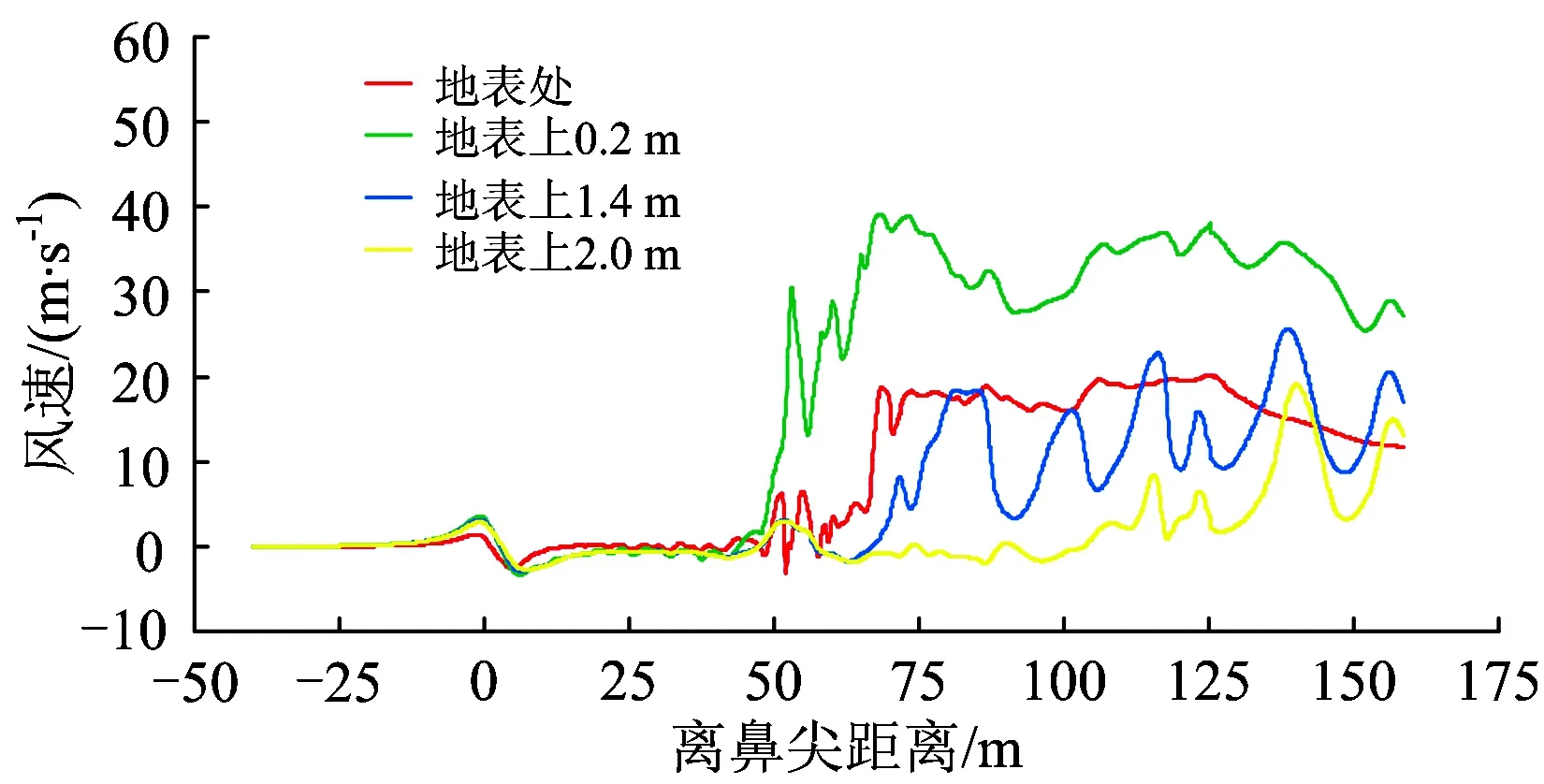
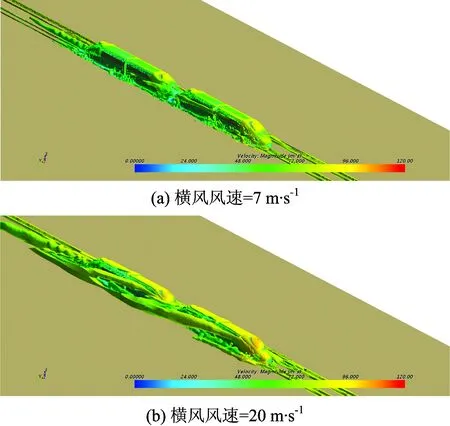
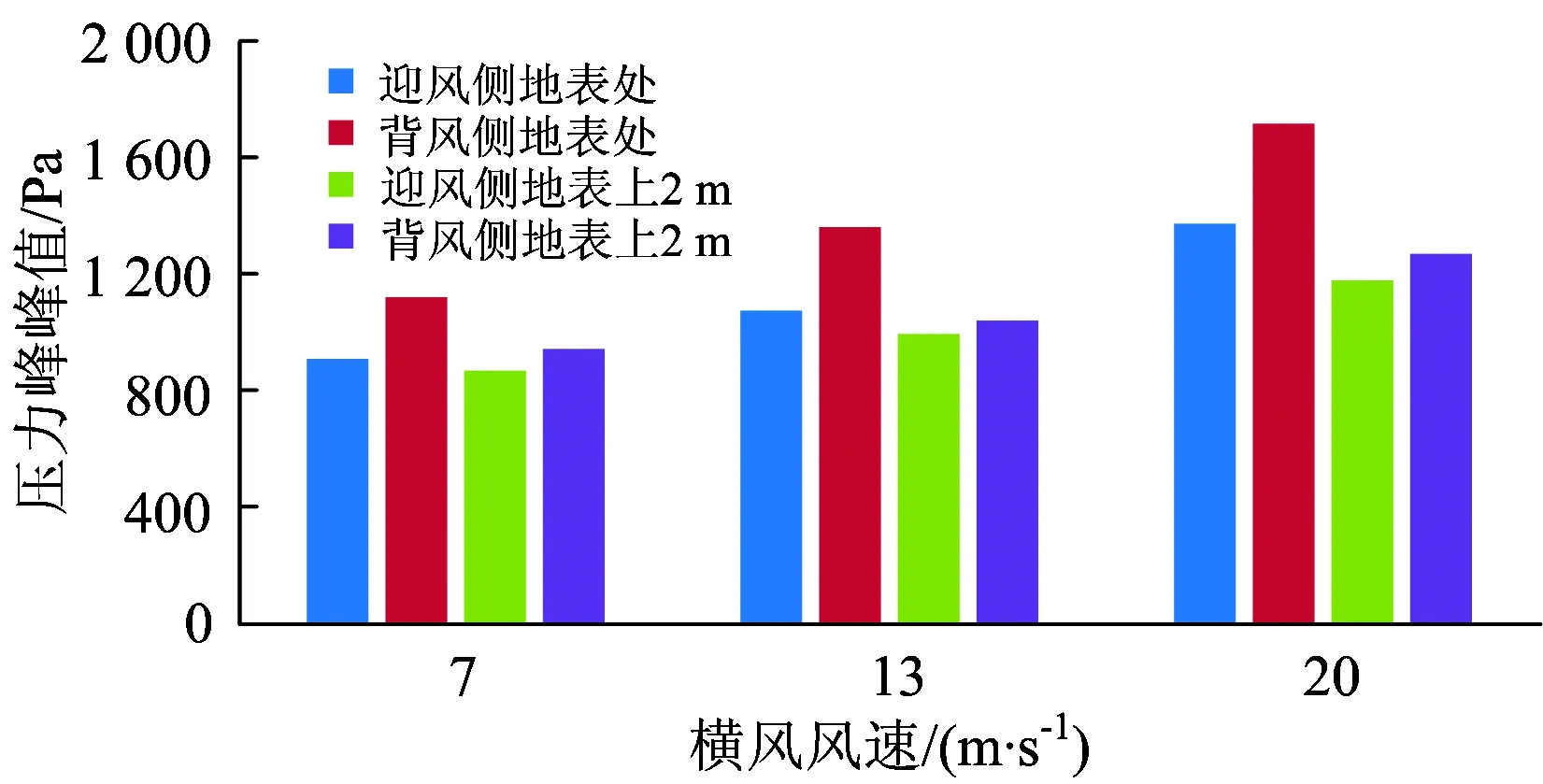
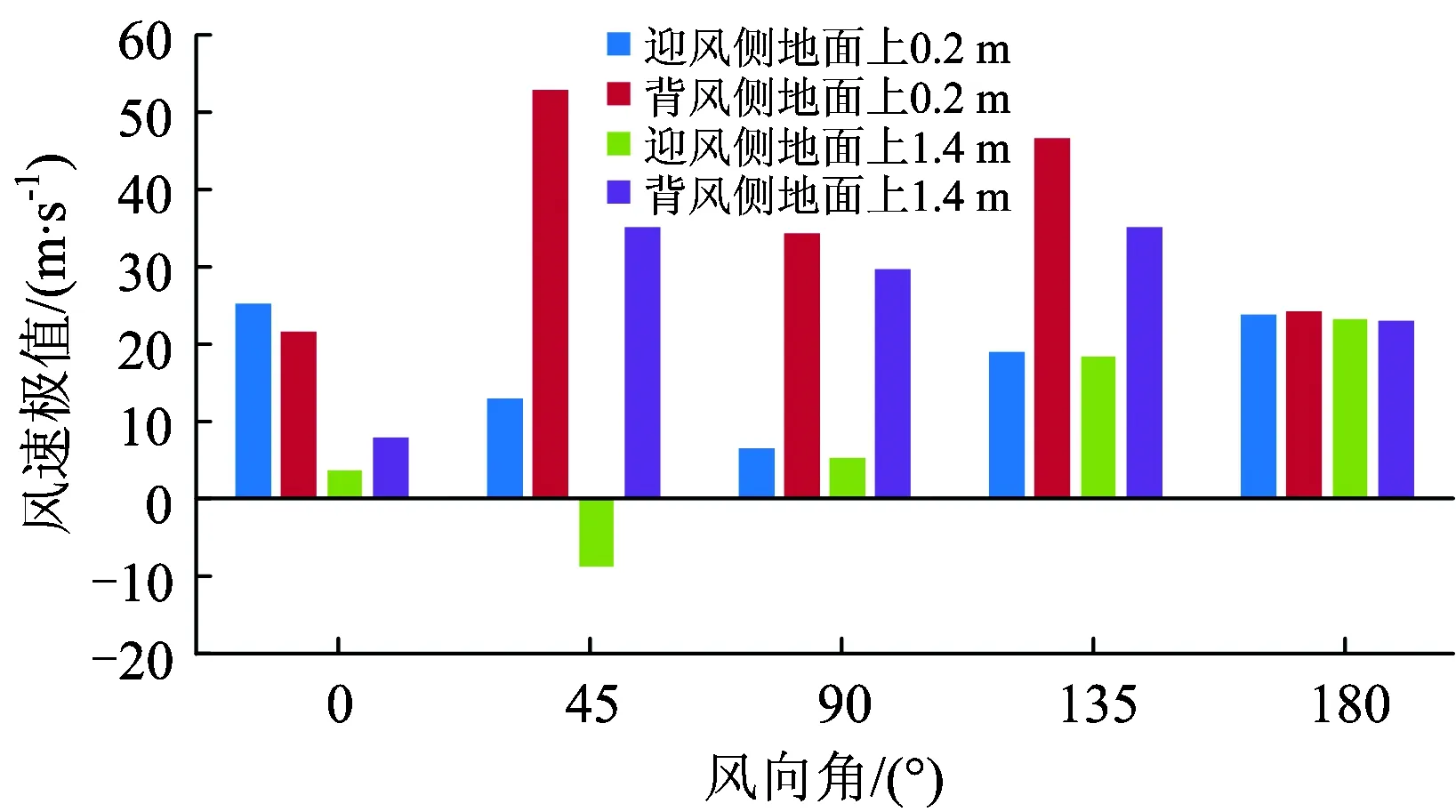
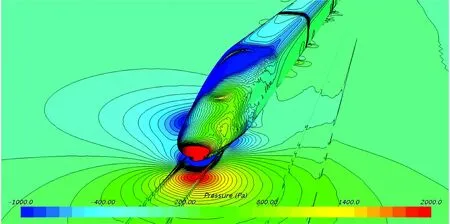
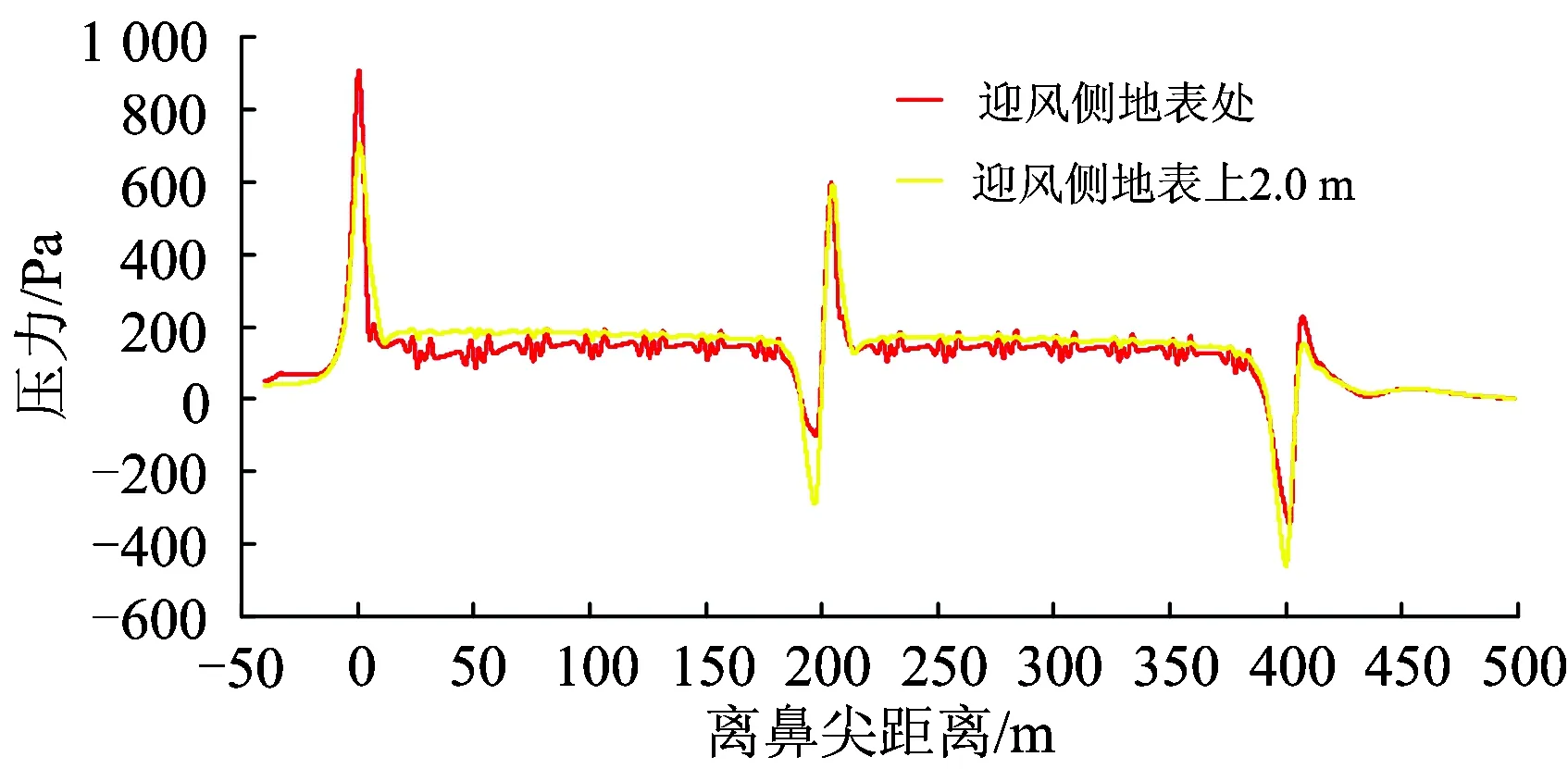
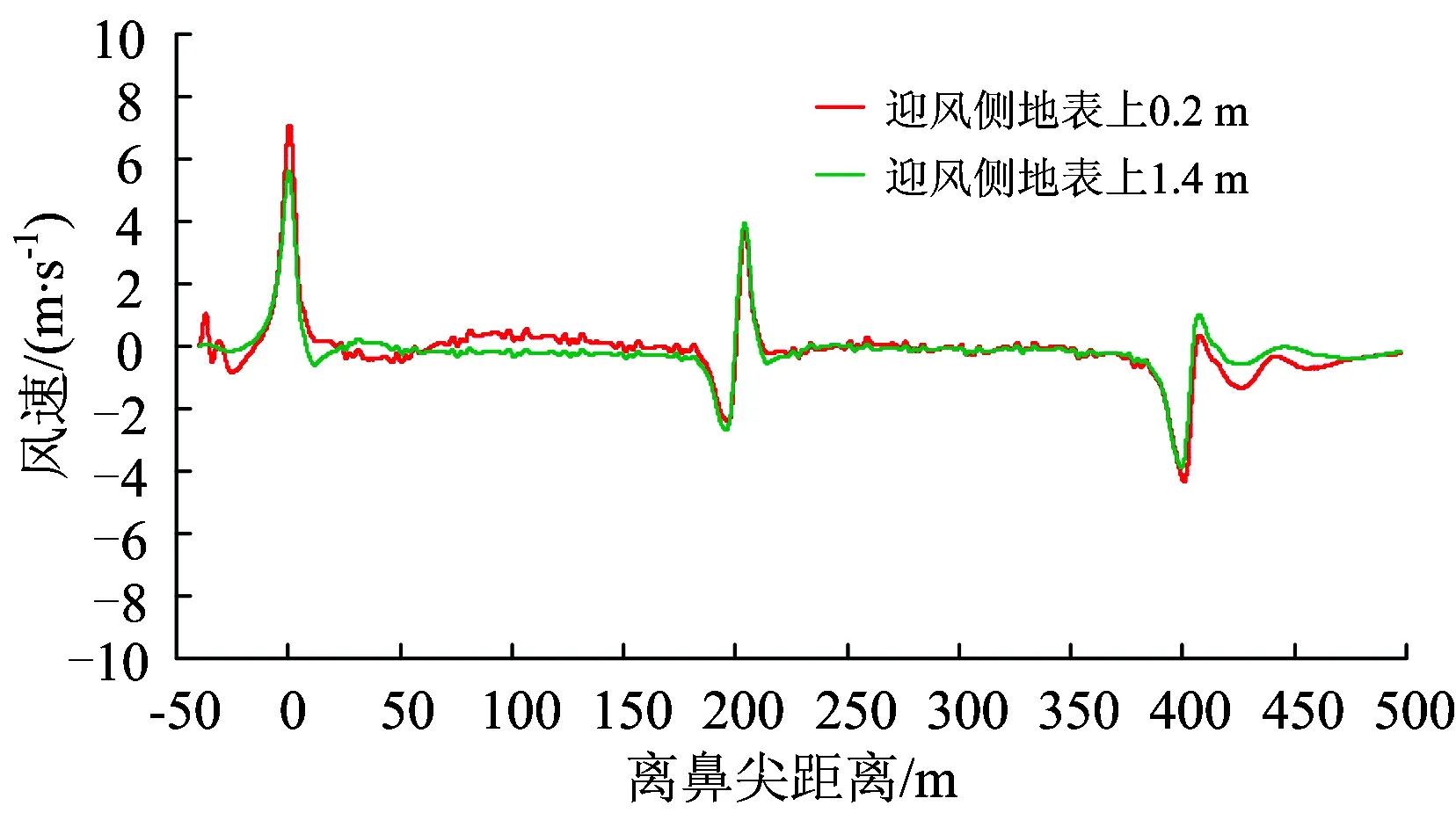
采用切割體網格對計算域進行有限體積劃分。為了捕捉到流場中的小尺寸結構,在車身、轉向架、風擋以及尾部等區域進行了局部加密。此外,為了準確地模擬列車車身及風擋等壁面區域的流動,捕捉到車身處流動的附面層沿壁面逐漸向外部空間區域發展的過程,在壁面區域使用了附面層網格,且其Y+(第1層網格質心到壁面的無量綱距離)應達到相關要求(30 圖3 計算網格 使用有限體積法,基于Navier-Stokes方程對計算域內的列車風流動參數進行求解[8]。流場的控制方程為 (1) 由于上述方程組不封閉,僅僅依靠式(1)對流場進行求解是不足夠的,需引入適當的湍流模型。因此,在列車風流場的仿真中使用已經得到了廣泛應用的SST k-omega湍流模型,該湍流模型對湍流參數求解的控制方程可以參照文獻[9]。風速—壓力耦合采用SIMPLC算法。為了使計算達到有效的精度,空間以及時間離散均采用2階。 風洞試驗與數值計算所使用的模型如圖4所示。 圖4 風洞試驗與數據計算模型 在風洞試驗模型側邊近地表附近設置壓力孔,通過壓力傳感器采集壓力。風洞試驗模型側邊開孔距離軌道中心線0.18 m,測試風速為50 m·s-1。風洞測點布置范圍為距離列車前鼻尖前方0.105 m至后鼻尖后方0.148 m,約為1節車長,足夠捕捉到列車流線型部分引起的壓力波動。風洞試驗與數值計算結果的對比如圖5所示。 圖5 風洞試驗與數值計算結果對比 從圖5可以看出:數值計算與風洞試驗結果吻合得很好,表明所采用的數值計算模型和方法對列車風流場關鍵參數的獲取是準確的。 列車在運行過程中,其車身周圍空間以及地表的壓力和風速是隨時間波動變化的。按列車風標準要求(TSI232),本文列車風的壓力主要考察距離軌道中心線2.5 m處地表及以上空間測點的壓力峰峰值,即整個時程的壓力最大值與最小值之差;列車風的風速主要考察距離軌道中心線3.0 m處地表及以上空間測點風速。 需要說明的是,由于列車風的最主要成分為縱向的流速,因此文中主要考慮的風速為縱向列車風。因為使用相對風速法給定來流條件模擬列車的運行,所以計算中得到的風速實際上是以列車為參照物,而實際情形下列車經過時引起的列車風應該是以地面為參照物,因此對計算得到的風速進行坐標變換[10],即經過坐標變換后得到的以地面為參照物的列車風縱向風速。 無橫風條件下,列車以300 km·h-1的速度運行時,距軌道中心線2.5 m地表處及其上較高空間處列車風的壓力變化時程曲線如圖6所示。從圖6可以看出:當重聯列車在無橫風條件下運行時,列車風均在車頭、車尾以及重聯處出現幅度較大的壓力波動;車頭處為先正后負的壓力脈動,尾車處與之相反,壓力脈動為先負后正,重聯處則出現正向壓力脈動。 圖6 列車風壓力變化時程曲線 無橫風條件下,列車以300 km·h-1的速度運行時,距軌道中心線3 m地表處及其上較高空間處列車風的風速變化時程曲線如圖7所示。從圖7可以看出:列車風通過列車頭部等截面變化較大區域時,其風速變化較大。此外,在尾流區域列車風的風速較大,且呈現波動的趨勢,這是由于列車的尾部存在尺度較大的渦結構,且隨著距離尾車的距離增大而逐漸向兩側分離脫落,在渦核區域則存在較大的流速,因此造成了尾部區域復雜的流動現象且出現了較大的風速。 圖7 列車風風速變化時程曲線 本節以上行線列車在橫風風速分別為7,13和20 m·s-1時的工況進行討論。 實際情形下列車風流場往往具有較大的雷諾數,這就表示列車處于較大的湍流環境中,列車風流場伴隨大量渦流結構的不斷生成和脫落。列車風流速和壓力的變化也是這一周期過程作用的結果。近年來,為了更加直觀地描述不同運行條件下的列車風,國內外學者往往采用對渦流結構實現可視化的方法。Hunt等人[11]提出的渦量Q的評判方法是對渦流結構實現可視化的重要方法。不同橫風風速下,Q=4 000時列車風風速的等值面如圖8所示。圖中:著色標量為列車風的風速。 圖8 不同橫風風速下Q=4 000時的列車風速等值面 從圖8可以看出:當列車處于橫風環境下運行時,在列車的背風側出現明顯的渦流結構[12],在這一區域內列車風的壓力和風速存在較大的波動;橫風風速較小時,從列車車身脫落的渦結構基本上沿車身方向分布,且集中在尾車以及重聯處;橫風風速較大時,尾渦偏向背風側的偏角更大,且車頭也出現明顯的流動分離而引起的渦脫,進而在列車的背風側形成更大的渦流區域。 不同橫風風速下、上行線列車距線路中心線2.5 m地表處及其上2 m空間處列車風的壓力峰峰值如圖9所示。從圖9可以看出:當存在橫風時,背風側地表相對于其上2 m處而言,其列車風壓力峰峰值更大;此外,隨著橫風風速的增加,相同位置處列車風壓力峰峰值也變大。其中橫風風速為20 m·s-1這一惡劣工況下,迎風側地表處及其上空間處的壓力峰峰值分別為1373.7和1178.6 Pa,背風側的則為1 718.9和1 271.0 Pa。 圖9 列車不同橫風風速下壓力峰峰值 不同橫風風速下,上行線列車距軌道中心線3 m地表上0.2和1.4 m空間處的風速極值如圖10所示。 圖10 列車不同橫風風速下風速極值 從圖10可以看出:在橫風條件下,近地表區域列車風的風速極值均大于較高空間處的;相對于迎風側而言,背風側列車風的風速極值更大。對于上行線列車而言,橫風風速使得不同位置處列車風的風速呈現逐漸上升的趨勢,橫風風速為20 m·s-1時,迎風側0.2和1.4 m空間處列車的風速極值分別為6.2和5.5 m·s,而背風側的則為52.5和35.9 m·s-1。 本節考察橫風風速維持在20 m·s-1,風向角分別為0°,45°,90°,135°和180°時,下行線列車列車風的分布特性。其中,風向角為0°代表列車逆風行駛,風向角180°代表列車順風行駛,風向角的定義如圖11所示。 圖11 風向角的定義 不同風向角下,Q=4 000時列車風風速的等值面如圖12所示。 圖12 不同風向角下列車外部流場Q=4 000時的等值面 從圖12可以得出:不同風向角下下行線列車周邊流場的分布規律大致相同;當列車運行方向與環境風平行,即列車的風向角為0°以及180°時,僅在列車車底、重聯區域以及車尾出現渦流區域,且尾渦脫落后基本處于離地面較近的區域;此外,在風向角為0°即列車逆風行駛時,渦流區域比180°風向角情況下更大,這是由于風速與車速合成后,0°風向角實際上的來流速度較180°的來流速度而言更大,因此出現了圖12所示的狀況;當列車處于90°風向角時,列車周圍的流動狀況較為復雜,此時列車背風側出現大量的渦結構,這一區域的速度、壓力場更為復雜。 不同風向角下,下行線列車迎風側距軌道中心線2.5 m地表處及其上2 m空間處列車風的壓力峰峰值變化如圖13所示。從圖13可以看出:風向角對列車迎、背風側的壓力分布有影響,風向角為45°時,地表及其上空間處列車風的壓力峰峰值均達到最大;在風向角從45°增加到180°的過程中,壓力峰峰值開始呈現下降的趨勢;由于橫風與列車運行這2個過程之間的相互耦合,在風向角從0°增加到180°的過程中并未呈現單調變化的趨勢;從測點高度來看,雖然地表區域及其上空間處均遵循上述變化特點,但是地表的壓力變化峰峰值始終大于其上空間2 m高度處的,45°風向角下,迎風側地表的壓力峰峰值最大達到1 420.2 Pa,背風側則達到了2 083.9 Pa。 圖13 列車不同風向角下壓力峰峰值 不同風向角下,下行線列車距軌道中心線3 m地表上0.2和1.4 m空間處列車風的風速極值如圖14所示。從圖14可以看出:由于環境風在列車行進方向上的分量會對列車風造成影響,因此不同風向角下的列車風極值分布規律較為復雜,但是總體來講,在有橫風的條件下,近地表區域的風速極值較大,背風側的大于迎風側的;當列車運行于45°風向角的條件下時,背風側近地表區域的列車風最大達到了52.9 m·s-1。 圖14 列車不同風向角下風速極值 以列車在下行線運行, 90°風向角、20 m·s-1橫風風速和45°風向角、20 m·s-1橫風風速2種工況為例,說明列車在8+8重聯編組條件下,車身周圍列車風壓力、速度的分布規律。45°風向角、20 m·s-1橫風風速、8+8編組條件下Q=4 000時列車風風速的等值面和車身表面的壓力云圖分別如圖15和圖16所示。 圖15 8+8編組條件下列車車身風場Q=4 000等值面 圖16 8+8編組條件下列車車身表面壓力云圖(單位:Pa) 從圖15可以看出:8+8編組時,列車風隨環境風場的變化與2+2編組時有相近的特征;45°風向角、20 m·s-1橫風風速環境時,車身周圍的渦流區域范圍擴大,在車頭、重聯部位以及車尾斜后方均出現與車身位置呈一定偏角的渦結構,車頂與迎風側面的交界處也因橫風作用下的流動分離產生了較多的渦結構;當列車運行于20 m·s-1的橫風風速環境下時,8+8編組時列車風的主渦結構相對于2+2編組時偏移的角度更大。 從圖16可以看出:8+8編組時,頭車附近壁面的壓力分布與2+2編組時的類似;45°橫風時,車頭壓力駐點向迎風側偏移,車頭前方地面也出現更大的正壓范圍;車頭流線型表面則由于橫風風速的作用,出現較大范圍的負壓區域,同時在這一區域也會出現較大的流動分離。 90°風向角、20 m·s-1橫風風速、8+8編組工況下,列車風的壓力分布和風速變化曲線分別如圖17和圖18所示。 圖17 8+8編組條件下列車迎風側測點壓力變化曲線 圖18 8+8編組條件下列車迎風側測點風速變化曲線 90°風向角、20 m·s-1橫風風速下,8+8編組與2+2編組列車在相同車速下的列車風壓力峰峰值和風速極值的對比分別見表1和表2。 表1 45°風向角、20 m·s-1橫風風速下2種編組列車不同位置處列車風的壓力峰峰值對比 Pa 表2 45°風向角、20 m·s-1橫風風速下2種編組列車不同位置處的風速極值對比 m·s-1 綜合圖17、圖18以及表1、表2可以看出:當存在橫風時,與2+2編組相比,8+8編組列車的重聯部位到頭尾的距離有所不同,因此列車車頂以及背風側列車風的流動及車頭、車尾和重聯區域列車風的相互作用形式以及結果不一致,進而引起了壓力以及風速的空間分布差異。 (1)在無橫風或橫風風向平行于列車運行方向時,車尾及重聯區域有較多的渦流結構,且尾渦基本貼近地面區域脫落;在有橫風時,尾渦朝背風側區域發生偏移,列車的背風側出現復雜的渦流結構,且車頭處出現流動分離進而引起渦脫現象。 (2)列車周圍的壓力變化峰峰值與測點空間位置有關,從高度方向上來看,近地表區域壓力變化峰峰值大于空間2 m高度處的壓力測點。列車周圍的風速同樣與空間位置有關,0.2 m高度處的列車風極值大于1.4 m高度處的列車風極值。相對于迎風側而言,背風側測點的壓力峰峰值以及風速極值總體而言更大。 (3)橫風風速越大,上行線列車周圍壓力波動越大,列車風風速極值也越大。隨著橫風風速的增加,同一位置處列車風的壓力峰峰值變化更大,不同位置處列車風的風速極值呈現逐漸上升的趨勢。 (4)當橫風風向不同時,由于環境風與列車運行時前方來流之間相互耦合,風向角為45°時近地表區域和較高空間處列車風的壓力峰峰值達到最大,在風向角從45°增至180°的過程中,列車風的壓力峰峰值呈現下降的趨勢。 (5)8+8重聯編組時,列車周圍流動隨環境風場的變化以及頭車附近壁面的壓力分布狀況與2+2重聯編組的工況有相近的特征。當存在橫風時,由于重聯部位到頭尾的距離不一致,列車車頂以及背風側部位的流動與車頭、車尾以及重聯區域流動之間的相互作用形式以及結果不一致,進而引起了壓力以及風速的空間分布差異。
1.3 求解計算
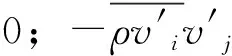
2 方法驗證

3 結果及分析
3.1 壓力、風速評價方法
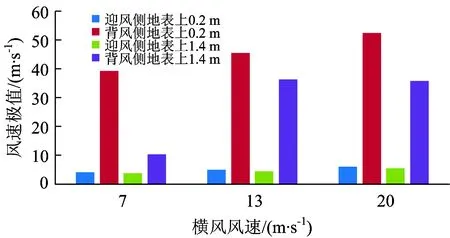
3.2 橫風風速對列車風特性的影響
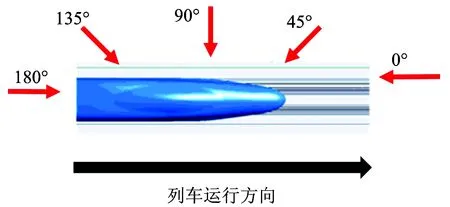
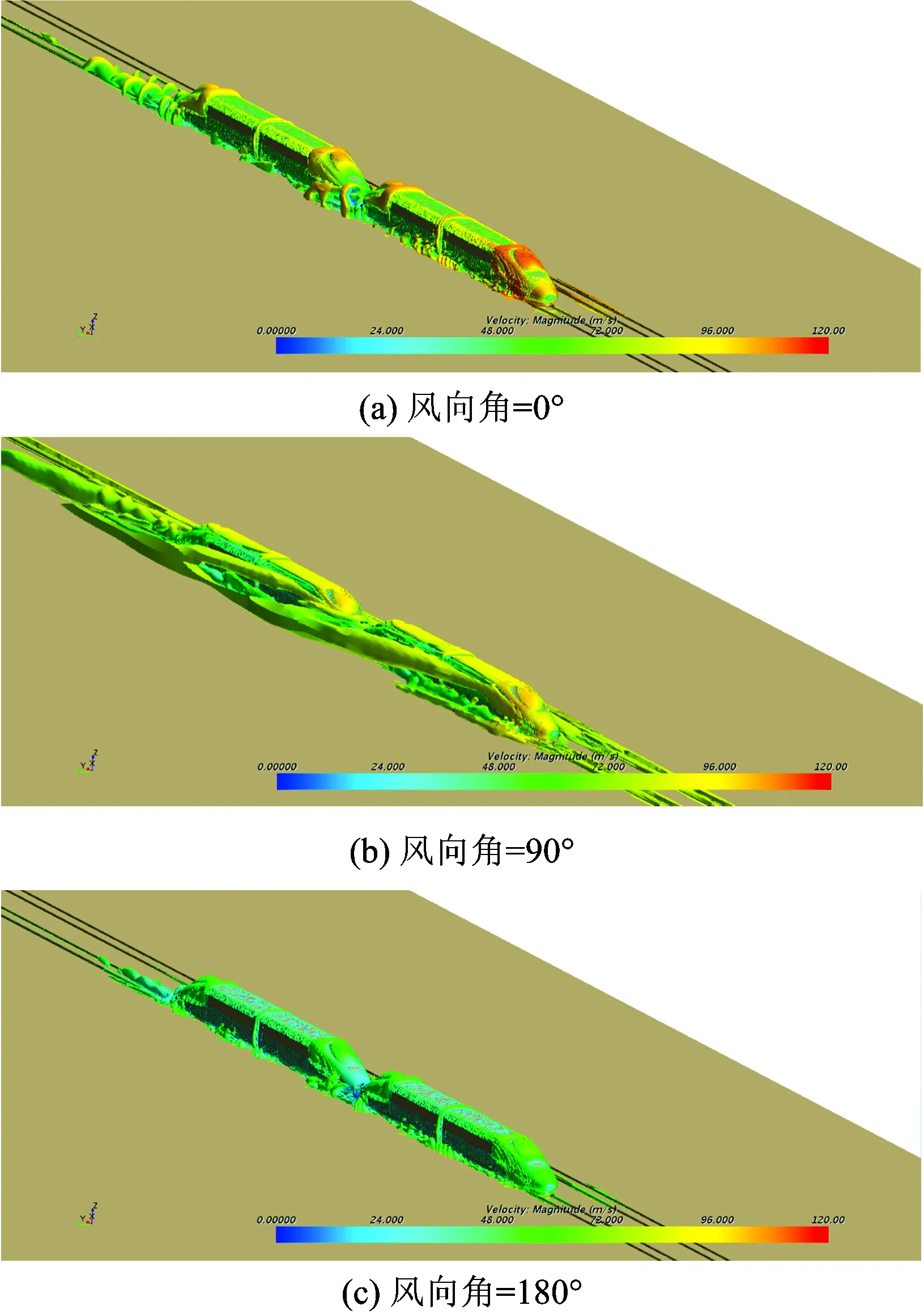
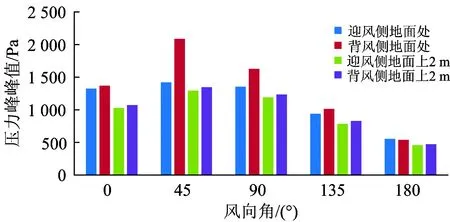
3.3 風向角對列車風特性的影響
3.4 編組形式對列車風特性的影響



4 結 論

