配電網諧波量測裝置最優配置方法

李 煒， 仉志華， 隋國正， 孫 東， 曲澤奇

(1. 中國石化股份勝利油田分公司技術檢測中心，山東 東營 257000; 2. 中國石油大學(華東)信息與控制工程學院，山東 青島 266580; 3. 勝利油田河口采油廠，山東 東營257200)

0 引言

近年來，為實現節能減排與生產工藝靈活調整要求，油田電網中變頻器等非線性電力電子設備日益增加，且有隨機接入系統的網電鉆機、網電修井機等設備，導致油田電網諧波源數量和類型不斷增加，諧波分布日趨復雜。諧波含量超標易造成補償電容器無法投入甚至爆炸、諧波諧振以及保護誤動作等問題，直接影響油田供電系統的安全可靠運行。所以，研究油田電網中諧波產生的機理、總結在油田生產設備中典型諧波源發生特性，分析諧波產生的影響十分必要。諧波在線監測系統為分析和掌握油田電網諧波發射與傳遞規律，提供了有效手段。諧波量測裝置費用高昂，從經濟角度考慮不可能所有節點全部安裝。同時，諧波狀態估計的可觀性和估計精度與量測量的數量、性質、位置以及系統網絡的拓撲結構密切相關。

Heydt等人提出利用系數矩陣最小條件數法進行諧波量測配置優化[1],但此法僅能得到保證量測方程有解的最小量測點數量，沒有涉及可觀性等。文獻[2]提出了關聯矩陣可以判斷可觀測性，但未給出具體方法。文獻[3]利用增廣關聯矩陣判斷系統可觀測性，且說明了冗余度對諧波狀態估計精度的影響，但其狀態量需要多次搜索，運算量大。文獻[4]提出了邏輯判斷法判斷可觀性，但只能判斷電流量測支路對側節點的可觀性。文獻[5]利用了網絡拓撲分析可觀性的方法，但其默認支路量測與節點電壓量測分離，運算量大，不適合現有裝置。

本文在文獻[5]的基礎上，一方面利用諧波量測裝置可以測量節點電壓及相關聯的所有支路電流的特點，改進了可觀性分析的算法，提高了運算效率；另一方面，引入可觀測度與冗余度的概念，達到了提高諧波狀態估計可觀測度與精度的目的。

1 諧波狀態估計基礎理論

諧波量測裝置量測量為節點電壓、支路電流和節點注入電流，狀態量為節點電壓。在電網絡的拓撲結構、支路參數以及量測裝置安裝布局已知的條件下，諧波狀態估計表達式為[6-7]：

Z=HX+ε

(1)

式中：Z為量測量，通過量測裝置直接讀取；H為量測方程，與線路的拓撲結構、線路的參數以及量測裝置的安裝布點有關；ε為量測誤差；X為要求解的狀態量。量測方程表示量測量與狀態量之間的關系，由以下三部分構成：

(1) 電壓量測方程：

Vm,i=IVT,i

(2)

式中：Vm,i為節點i諧波電壓量測量；VT,i為節點i諧波電壓狀態量；I為適當維數的單位矩陣。

(2) 節點注入量測方程：

(3)

式中：Im,i為節點i諧波注入電流量測量，中間節點的諧波注入電流值為0；VT,j為節點j諧波電壓狀態量；yi,j為節點導納矩陣中對應節點i和j的分塊導納矩陣元素；n為網絡節點總數。

(3) 支路量測方程：

Ii,j=Yi,j(Vi-Vj)

(4)

式中：Ii,j為節點i到j之間支路的電流；Vi和Vj為節點i和節點j的節點電壓；Yi,j對應節點i和j之間的導納矩陣。

2 諧波狀態估計的可觀性邏輯判斷方法

諧波量測配置理論基于諧波狀態估計可觀性分析。可觀性分析就是在已知系統網絡拓撲結構和量測裝置配置的基礎下，通過利用量測裝置提供的數據來確定未知節點狀態的能力[8-9]。若基于量測裝置提供的數據通過量測方程能夠得出整個系統節點的電壓或電流相量，即通過對系統狀態估計可以使系統各節點狀態已知，此時系統網絡視為完全可觀。若基于量測裝置提供的數據通過量測方程不能得到整個系統的節點電壓或電流相量，則此時系統網絡不可觀或不完全不可觀。

諧波狀態估計的可觀性邏輯判斷方法主要基于前文的3類量測方程。由于諧波量測裝置不僅可測所安裝節點的電壓，還可測與該節點相關聯的所有支路的電流，因此諧波狀態估計的可觀性有下列特點[10-14]：

(1) 若節點存在量測裝置，則該節點的狀態完全可觀；(2) 在本側節點電壓可觀時，支路電流量測使與該量測支路互聯的對側節點的狀態可觀；(3) 若某支路兩端的節點電壓均可觀時，則該支路的電流可觀；(4) 若某節點無可疑諧波源，且該節點沒有配置量測裝置，若該節點相連所有支路電流僅有一個未知，則可根據基爾霍夫電流定律對該支路電流進行求解，該支路電流可觀。

可見，當量測配置選在包含支路關聯關系最多的節點時，其可觀的范圍最大。

3 量測配置優化方法

量測裝置的優化布點根據優化目的的不同，大體可以分為幾類：(1) 出于經濟性考慮，配置最少的量測裝置，達到最大程度的可觀。(2) 配置較少的量測裝置，優先考慮使諧波狀態估計達到一定精度，其次達到最大程度的可觀。(3) 配置一定的量測裝置，優先考慮達到最大程度的可觀，其次使諧波狀態估計達到一定精度。

系統可觀測范圍可由可觀測度表示，可觀測度[15]是指可觀測的節點數與電網絡中總節點數的比值，可觀測度為1則表示系統完全可觀。同時在可觀的情況下，考慮系統的冗余度，冗余度[15]為量測點被重復測量的次數。文中量測裝置的優化布點，是通過配置一定數量的量測裝置，使其達到系統的最大可觀，當不同量測配置方案的可觀性一致時，優先選擇冗余度最大的方案。

根據諧波狀態估計可觀性的特點，文中將節點的可觀性分為直接可觀和間接可觀[16-22]。直接可觀判斷依據可觀性特點(1)、(2)、(3)，通過關聯矩陣進行一次運算即可判斷；間接可觀判斷依據可觀性特點(4)，須對關聯矩陣進行二次運算得到。綜上，量測配置優化分為2個步驟：

(1) 直接可觀節點判斷。以系統的可觀測度為目標，假設系統的節點數為n，有k個量測配置方案，建立量測裝置的優化布點函數：

(5)

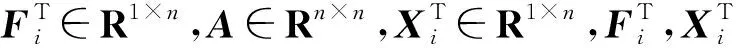
通過此步驟，可以判斷出每種量測配置方案下除本身裝有量測裝置的節點外直接可觀的節點，即新增直接可觀節點，以及各直接可觀節點重復測量的次數即冗余度。

(2) 間接可觀節點判斷。對于第i個量測配置方案下新增的直接可觀節點m，有：

fm=Am-Xi

(6)

式中：Am為關聯矩陣的第m行，表示m節點與各節點之間的關聯關系；Xi為第i種量測配置方案。

若fm中，除第m列外，僅有一列元素為1，則該列對應節點可觀，Fi中該列元素加1；對各量測配置方案的所有新增直接可觀節點重復執行步驟(2)。

完成所有步驟后，分析F中的每一行(即每種量測配置方案)的元素，對每種量測配置方案下的可觀測度和冗余度進行比較，選擇可觀測度最大的量測配置方案為最優配置方案，若有多個量測配置方案可觀測度同時最大時，選擇冗余度最大的量測配置方案。上述過程流程圖如圖1所示。

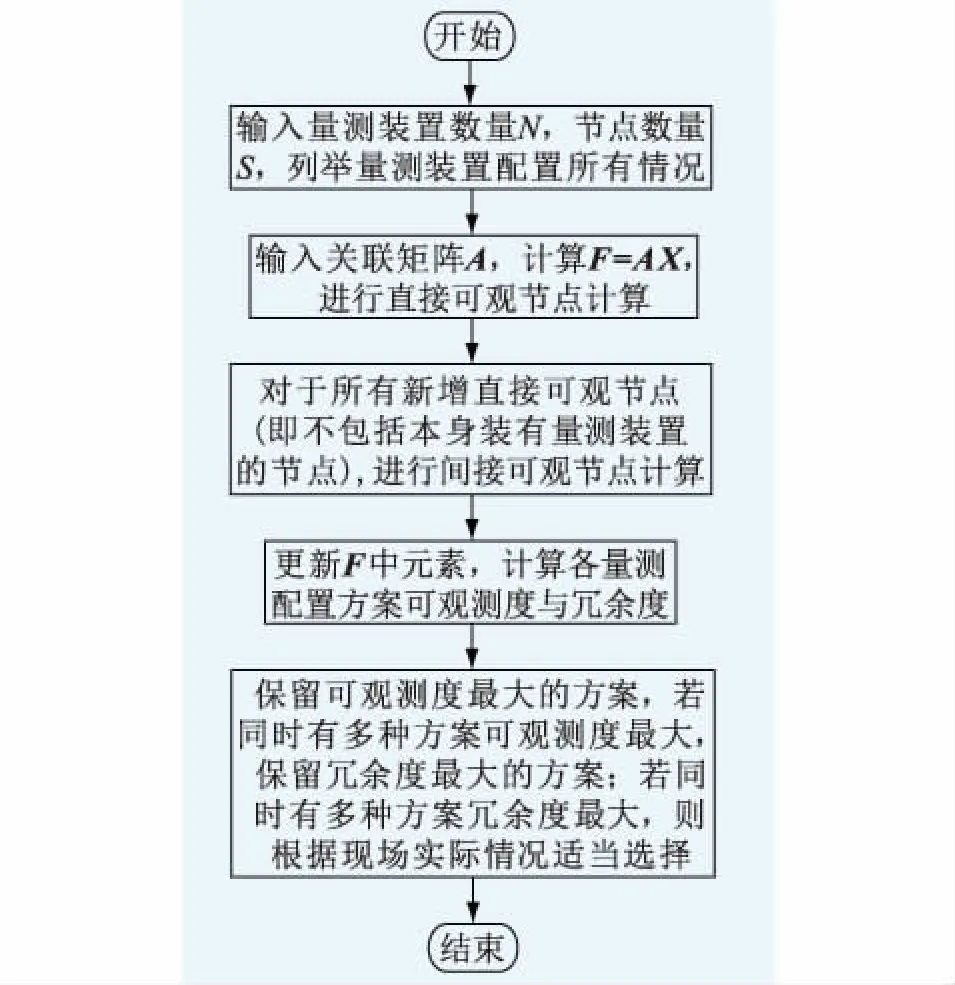
圖1 量測配置優化流程Fig.1 Flow chart of measurement configuration optimization

4 算例分析

本算例以勝利油田河口采油廠大一變電所某饋線為研究對象，在線路上選取節點布置量測裝置。對該線路模型進行簡化，簡化圖如圖2所示。根據線路模型簡圖，關聯矩陣A如下：

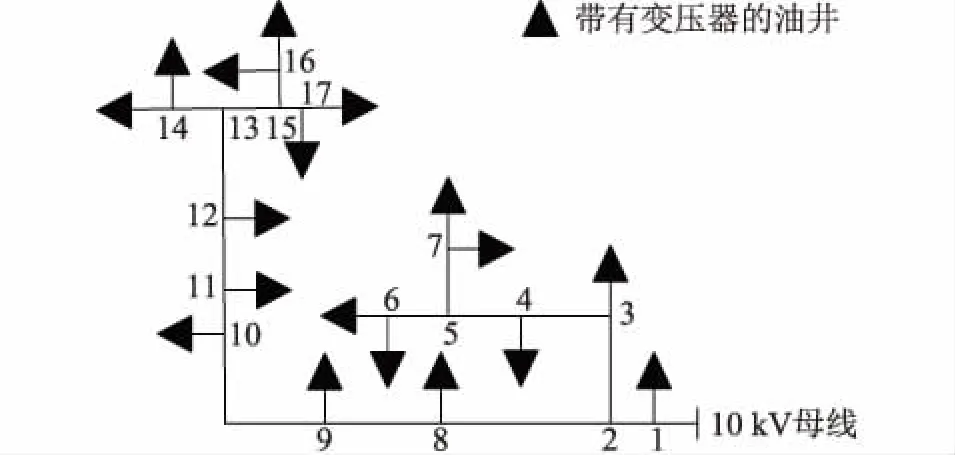
圖2 線路模型簡化圖Fig.2 Simplified schematic of Oilfield distribution network line

(1) 當量測裝置數量分別為3和4時，對關聯矩陣進行可觀性分析，得到量測配置優化布點結果如表1所示。從表1中可以看出，當量測裝置數目為3時，共有2種配置方案可供選擇，2種策略可觀測度和冗余度相同，均為系統部分可觀且達到系統最大可觀測度，且量測冗余度均為0，可根據油田現場實際情況選擇合適的配置方案；當量測裝置數量為4時，共有3種配置方案可供選擇，系統最大可觀測度達到0.882 353，且量測冗余度均為0。

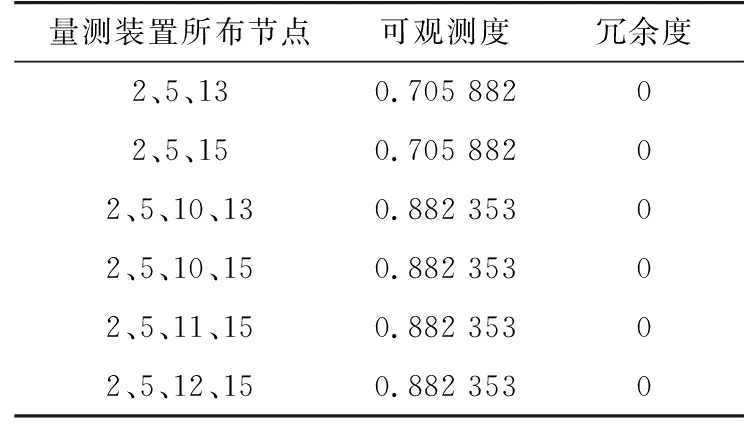
表1 量測裝置布點方案Tab.1 Measuring device layout scheme

(2) 當量測裝置數量為5時，利用關聯矩陣進行可觀性分析，量測配置優化布點結果如表2所示。

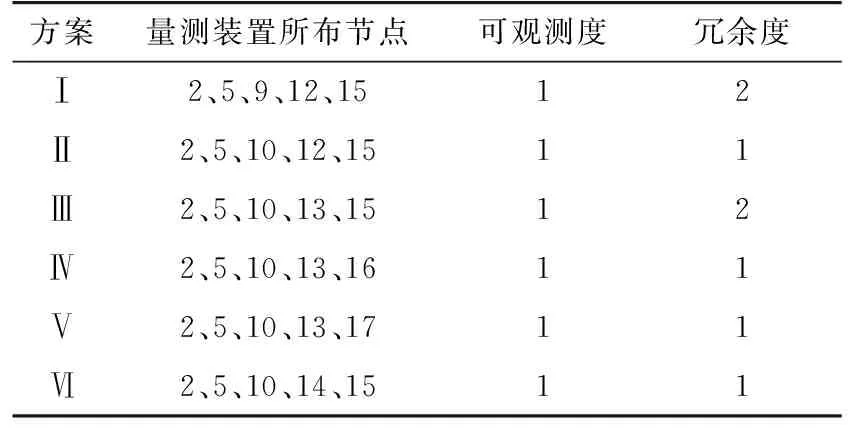
表2 考慮系統可觀測度最大的量測優化布點方案Tab.2 Optimized layout scheme considering the maximum observability of the system

由表2可以看出，當量測裝置數量為5時，系統可以達到完全可觀的布點方案有6種，但其冗余度并不相同，此時，從狀態估計精度角度考慮，選擇冗余度最大的方案，即方案Ⅰ與方案Ⅲ。

由于油田現場實際情況復雜，有些節點施工難度高，不便于安裝量測裝置，且不同節點負載特性不同，因此可適當選擇量測配置方案。

(3) 當量測裝置為5時，采用表2中方案Ⅰ作為諧波量測裝置配置方案，進行諧波狀態估計，以5次諧波為例，量測量如表3、4所示，表4中支路編號“2—1”指節點2與節點1之間支路編號，支路電流量測方向為節點2指向節點1，其他支路同理。狀態估計結果如表5所示，其中誤差指估計值相對于仿真值的誤差。

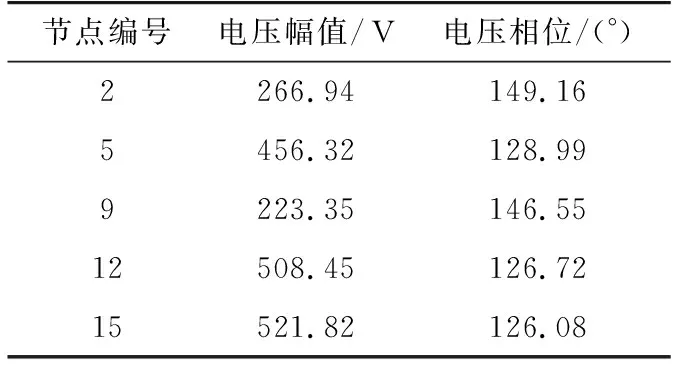
表3 節點電壓量測量Tab.3 Measurement of node voltage

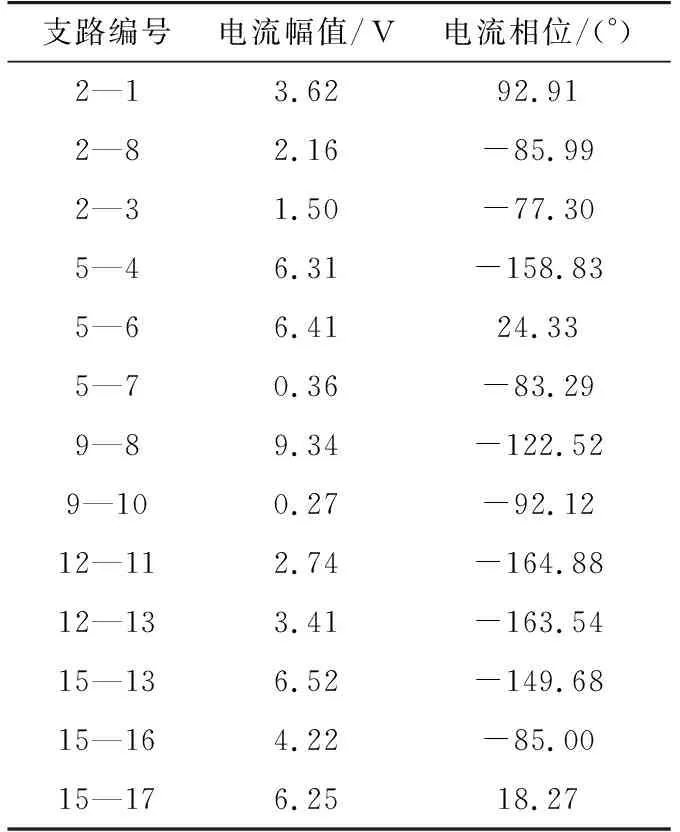
表4 支路電流量測量Tab.4 Measurement of branch current

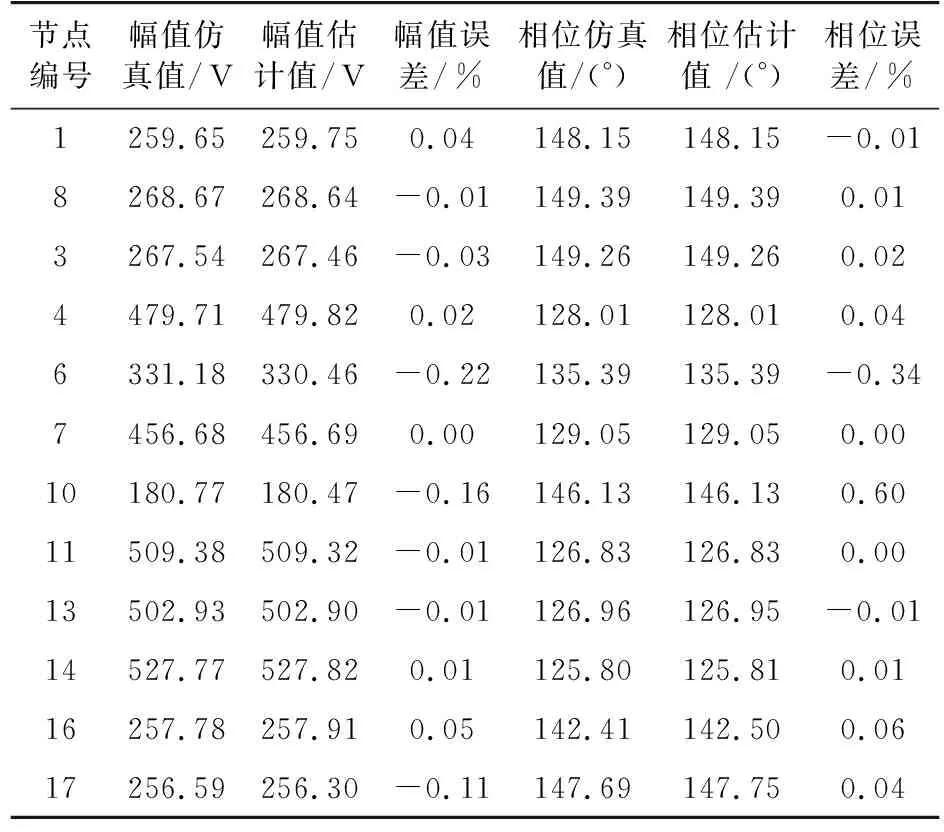
表5 5次諧波電壓幅值和相位誤差對比Tab.5 5th harmonic voltage amplitude and phase error comparison

可以看出，根據表2的方案Ⅰ，系統達到了完全可觀，且精度較高，誤差較小。

5 結語

由于油田配電網網絡拓撲結構復雜，節點支路眾多，諧波源分布不規律，較為分散，使得諧波狀態估計量測裝置配置不要求實現全局可觀。本文的量測裝置最優配置方法，在給定量測裝置數量的情況下，可以實現最大程度的可觀。且本方法通過關聯矩陣進行計算，由于關聯矩陣的稀疏性，使得量測裝置配置原則簡潔明了。當不同的量測裝置配置方案可觀測度相同時，優先選取量測冗余度最大的量測裝置配置方案，提高狀態估計的精度。并針對勝利油田河口采油廠大一變電所某饋線進行量測裝置配置優化，分別給出了當量測裝置數目為3、4、5時的量測裝置配置方案，并根據配置方案，給出了量測裝置數目為5時的諧波狀態估計結果，結果表明系統達到完全可觀，且誤差較小。算例驗證了本方法的有效性。