有軌電車特小半徑曲線受力和變形特性

吳青松，段曉暉

(1.中交城市軌道交通設計研究院有限公司，湖北 武漢 430056；2.中交第二公路勘察設計研究院有限公司，湖北 武漢 430056；3.中鐵第四勘察設計院集團有限公司 線站處，湖北 武漢 430063)

現代有軌電車線路投資少，建設周期短，具有節能環保、安全舒適、運能靈活等特點。現代有軌電車車輛采用獨立輪對，左右2車輪解耦，獨立轉動[1]，在曲線軌距不加寬條件下，能通過的最小曲線半徑為15～30 m[2-4]。由于城市地形及道路條件限制，部分線路通過路口時采用特小半徑曲線，通常半徑為50 m。沈陽市渾南新區現代有軌電車采用一次建成槽形軌無縫線路，鋪設半徑為25～50 m的特小半徑曲線共計20余處；武漢市大漢陽地區現代有軌電車無縫線路曲線最小鋪設半徑為50 m。

關于無縫線路鋪設，TB 10015—2012《鐵路無縫線路設計規范》[5]允許鋪設無縫線路的最小曲線半徑為300 m；GB 50157—2013《地鐵設計規范》[6]中規定地下線曲線半徑不小于300 m地段、高架線及地面線無砟道床曲線半徑不小于400 m地段宜按無縫線路設計，允許最小曲線半徑均未突破300 m。現代有軌電車允許最小曲線半徑為35 m，困難條件下可至25 m[7]，最小曲線半徑為25～35 m已遠遠突破前述2個規范的限值。因此，有必要對有軌電車特小半徑曲線段受力和變形特性進行研究。

研究有砟軌道無縫線路穩定性時采用統一的無縫線路穩定性計算公式[5]，該公式有特定的使用條件，不適于有軌電車特小半徑曲線段的研究。有軌電車整體道床結構剛度大，橫向抗彎剛度為豎向的b/h2倍(其中b為寬度，h為高度)；且由于上覆層的存在，道床結構溫度變化較小，橫向失穩可能性很小。為了綜合考慮無縫線路下部整體道床對無縫線路受力和變形的影響，本文借助有限元軟件進行研究。

1 計算模型

1.1 鋼軌-道床三維空間耦合力學模型

以某有軌電車線路為例，特小半徑曲線段為硬化鋪裝整體道床。受限于城市道路條件，通常不設置超高。軌道結構從上到下依次為60R2槽形鋼軌、無枕式扣件、道床板、支承層和路基，扣件直接錨固于道床板，道床板與支承層通過層間黏接形成整體。曲線段線路受氣溫變化影響，鋼軌、道床內部蓄積較大的溫度力。隨著溫度力的增大，鋼軌、道床發生變形，釋放部分溫度力，表現為徑向分力，通過扣件傳遞至下部道床結構。此外，列車在通過曲線時，輪緣貼靠鋼軌產生橫向荷載，制動產生制動荷載，均通過扣件傳遞至下部道床結構。本文根據軌道結構縱橫向受力特點，利用有限元軟件建立鋼軌-道床三維空間耦合力學模型，如圖1 所示。

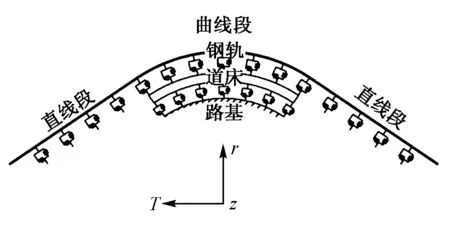
圖1 鋼軌-道床三維空間耦合力學模型

模型由直線段-曲線段-直線段組成，直線段和曲線段直接相連，未考慮緩和曲線連接。其中鋼軌采用三維梁單元模擬，道床板、支承層采用實體單元模擬，扣件分別采用縱、橫、垂3個方向的彈簧單元模擬。道床板與支承層間采用黏接模擬，支承層與路基間相互作用采用彈性地基模擬。考慮到扣件對鋼軌的限位作用隨線路方向的變化而變化，在直線段采用直角坐標系，x,y,z分別為線路縱、橫和垂向;在曲線段采用柱坐標系，r,T,z分別為線路橫、縱和垂向。

模型假定：①本文僅從軌道結構自身受力變形的角度出發，不考慮埋入式軌道硬化鋪裝及柔性材料；②假定直線段長度(100 m)足夠消除邊界條件影響，鋼軌兩端采用固定約束；③不考慮鋼軌初始彎曲及運營維護線形偏差。

1.2 主要計算參數

參照統一公式，無縫線路臨界容許溫度力與曲線長度L、曲線半徑R有關。為研究曲線長度、曲線半徑對無縫線路受力和變形的影響，模型選取不同的曲線半徑及曲線長度，最小圓曲線長度取15 m[7]，最大圓曲線長度以對應圓心角不超過180°進行選取，共計34種曲線半徑和曲線長度組合，具體見表1。

表1 不同曲線半徑R和曲線長度L所對應的圓心角 (°)

60R2槽形軌彈性模量為206 GPa，泊松比為0.3，熱膨脹系數為 0.000 011 8 /℃，橫截面積為76.11 cm2，橫向慣性矩為920.1 cm4；扣件垂向、橫向彈簧為線性彈簧單元，剛度取50 kN/m[8]；扣件縱向彈簧為非線性彈簧單元，極限位移2 mm，單組扣件阻力為9 kN，即單位長度扣件縱向阻力為14.4 kN/(m·軌)。道床板為C40混凝土，彈性模量為32.5 GPa，泊松比為0.2，熱膨脹系數為0.000 01/℃。支承層為C25混凝土，彈性模量為28 GPa，泊松比為0.2，熱膨脹系數為0.000 01/℃。

列車荷載：根據有軌電車列車荷載圖式[9]，列車橫向荷載取為靜輪載的0.8倍，即50 kN，單輪加載；加載位置分別為直圓點、圓曲線中點。

道床溫度取值：有軌電車軌道結構為埋入式，交叉路口硬化鋪裝覆蓋道床結構，道床結構上下溫差變化較小，因此不考慮道床結構溫度梯度。為考慮最不利影響，道床結構溫度變化范圍取氣溫變化范圍。以武漢地區為例，歷年最高氣溫39.6 ℃，最低氣溫-18.1 ℃，考慮混凝土施工溫度為10～20 ℃，道床結構最大降溫29.6 ℃，最大升溫38.1 ℃。考慮混凝土收縮影響，分段灌筑的道床結構取等效降溫10 ℃[10]。綜上，道床溫度取值最大降溫、最大升溫均取40 ℃。溫度力與列車荷載組合時，采用最大日溫差，日溫差(升溫或降溫)取為20 ℃。

鋼軌溫度取值：武漢地區歷年最高氣溫39.6 ℃、最低氣溫-18.1 ℃，取最高軌溫59.6 ℃、最低軌溫-18.1 ℃，設計軌溫為20±5 ℃，鋼軌最大升溫44.6 ℃、最大降溫43.1 ℃，均取為50 ℃。

1.3 荷載工況

特小半徑曲線段軌道結構隨著季節更替，鋼軌溫度偏離鎖定軌溫，道床溫度偏離施工溫度，在內部蓄積了較大的溫度力。升溫時，鋼軌、道床向外膨脹變形；降溫時，鋼軌、道床向內收縮變形，變形過程中均伴隨著溫度力的釋放。由于曲線段軌道結構存在初始彎曲，在溫度升高情況下容易失穩破壞。因此，本文僅分析溫度升高荷載工況。結合軌道結構實際運營情況，分析工況包含最大溫度荷載和常用荷載組合，共計11組荷載工況(橫向荷載作用位置包括直圓點和圓曲線中點)，具體見表2。綜合34種曲線半徑及曲線長度組合和11組荷載工況，共計374個計算工況。

表2 荷載工況

2 計算結果分析

2.1 最大溫度荷載對軌道受力和變形的影響規律

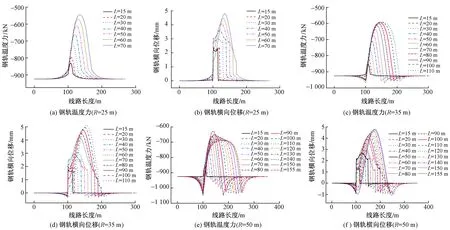
圖2 最大溫度荷載作用下鋼軌受力和變形

最大溫度荷載(工況1)作用下，鋼軌溫度力、橫向位移計算結果見圖2。可知，兩端直線段鋼軌溫度力趨于水平，鋼軌溫度力與無縫線路固定區溫度力一致，說明模型中鋼軌邊界條件假定合理。曲線兩端直線段可視為無縫線路固定區，鋼軌溫度力無釋放。直線段與曲線段之間為過渡段，此處鋼軌溫度力逐步被釋放，隨著曲線半徑的增加，該段出現向內位移(負位移)，半徑越大、長度越長，受到直線段固定區的擠壓越明顯，在直圓點處達到最大，主要原因是曲率變化不連續。曲線段為鋼軌溫度力釋放區，在連續支承層向外膨脹變形帶動下，鋼軌向外移動，整個鋼軌溫度力以曲線中點為中心呈對稱布置，在曲線中點處達到最大值，對應的橫向位移也達到最大值，鋼軌溫度力釋放量與鋼軌橫向變形呈對應趨勢。

綜合受力和變形情況可知，曲線中點處鋼軌溫度力釋放量最大，相對于直線段固定區，曲線半徑為25 m 時，溫度力釋放量隨曲線長度的增長而快速增大，其差值由94.3 kN增大至379.8 kN，最大橫向位移則由2.34 mm增至4.78 mm；曲線半徑為35 m時，溫度力釋放量隨曲線長度的增長先快后慢地增大，其差值由74.2 kN增大至333.3 kN，最大橫向位移則由1.78 mm 逐步增至5.13 mm，最大橫向負位移約為0.3 mm；曲線半徑為50 m時，溫度力釋放量隨曲線長度的增長先增后降，其差值由62.8 kN先增至298.2 kN，再緩慢降至236.8 kN，最大橫向位移則由1.35 mm逐步增至4.80 mm，最大橫向負位移由0.04 mm 增至1.09 mm。上述位移均為鋼軌絕對位移，包括鋼軌和道床的整體橫向變形，主要是道床向外膨脹變形帶動發生的，而鋼軌和道床間相對位移較小。相比于有砟軌道無縫線路橫向失穩限值2 mm，上述計算結果已遠超該限值，但由于無砟軌道剛度大，并未發生失穩破壞，軌道結構在最大溫度荷載作用下發生橫向向外4～5 mm的徑向位移時，位移量在合理范圍內，且此時軌道結構均處于線彈性階段。計算結果表明，有砟軌道無縫線路橫向失穩限值2 mm并不能很好地評價有軌電車特小半徑曲線無縫線路受力狀態。由于特小半徑曲線段軌道結構整體橫向位移較大，在鋼軌與硬化鋪裝銜接處應采用可變形材料，以適應變形，防止擠壓破壞。

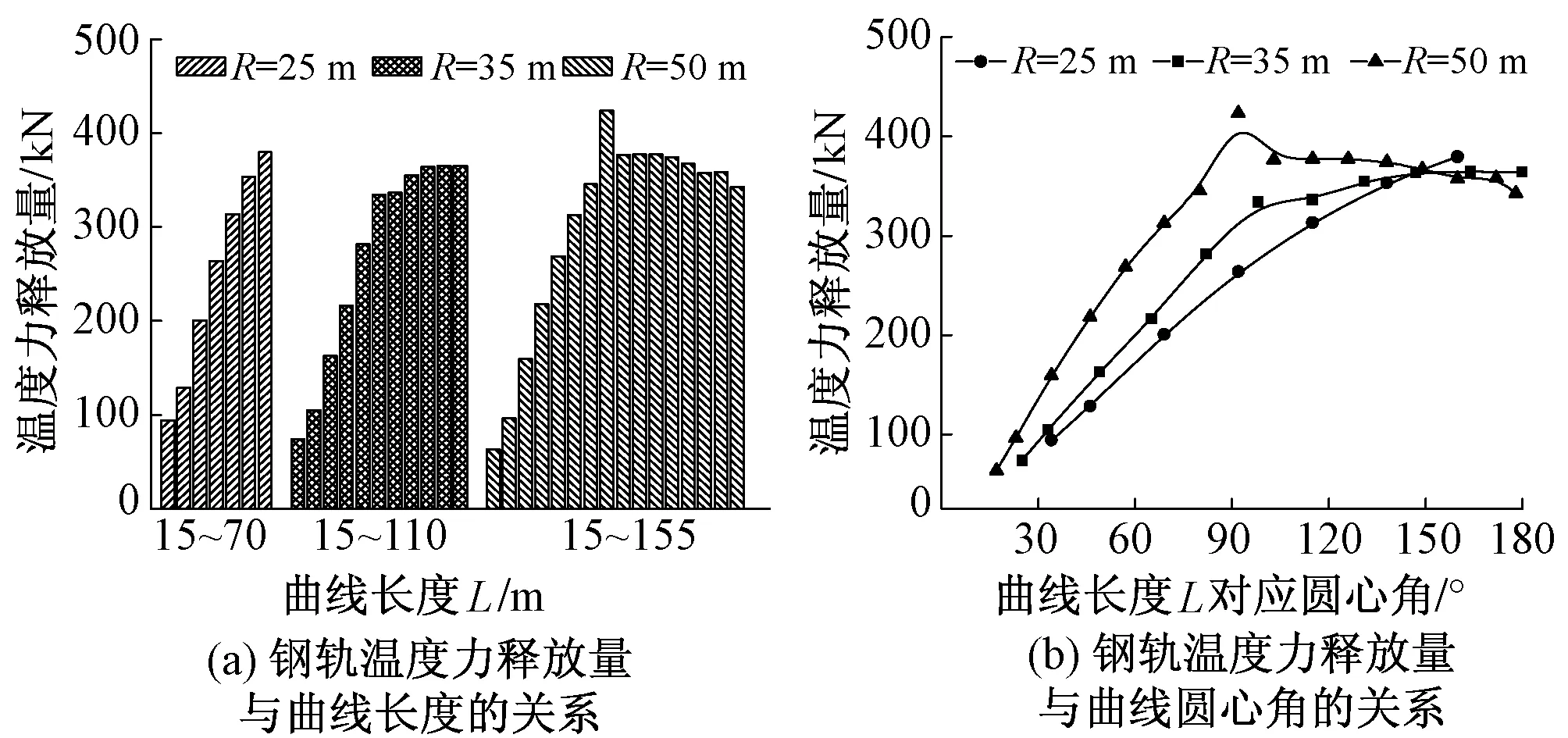
圖3 最大溫度荷載作用下鋼軌溫度力釋放量

圖3為最大溫度荷載作用下，考慮直圓點受壓后的鋼軌溫度力的釋放量。由圖3(a)可知，曲線半徑為25 m時，鋼軌溫度力釋放量隨曲線長度的增長而快速增大，由94.3 kN增大至379.8 kN；曲線半徑為35 m 時，溫度力釋放量隨曲線長度的增長先快速增大，曲線長度達到60 m后，溫度力釋放量增大速度降低，曲線長度為90～110 m時，溫度力釋放量幾乎不再增長，最大釋放量為364.8 kN；曲線半徑為50 m時，溫度力釋放量隨曲線長度的增長先快速增大，曲線長度達到80 m 后，溫度力釋放量增大速度降低，并出現釋放量減小的現象，曲線長度為80 m時，鋼軌溫度力最大釋放量為423.4 kN。由圖3(b)可知，以圓心角90°為分界線，圓心角小于90°時，溫度力釋放量增長速度較快，大于90°后則增速減慢；圓心角小于150°時，曲線半徑越小，溫度力釋放量越小，這主要是由于曲線半徑大則所對應的線路長，其下部支承層為連續結構，在溫度力作用下向外膨脹變形，會帶動無縫線路橫向位移和加大無縫線路溫度力的釋放。

結合實際選線工作，在線路經過路口時，通常線路中線是確定的，即線路偏轉角(圓心角)確定，此時，可選用較小曲線半徑通過路口。但曲線半徑太小會限制有軌電車允許通過速度，延長通過路口時間，對交通影響較大，應綜合考慮。

2.2 常用荷載對軌道受力和變形的影響規律

由前述分析可知，無縫線路在直圓點受到直線段固定區的擠壓，承受較大的溫度力；而圓曲線中點處橫向位移、溫度力釋放量均達到最大。上述2處是無縫線路薄弱點，因此本文在常用溫度荷載基礎上，在上述2點分別施加橫向荷載，以研究常用荷載對軌道受力和變形的影響規律。

軌道結構在常用溫度荷載作用下，鋼軌變形規律與前述最大溫度荷載作用類似，在曲線段釋放溫度力。由于列車橫向荷載的作用，在作用點兩側形成受力突變，左側鋼軌受力得到一定的釋放，而右側因受到無釋放段擠壓，反而有所增長。由于軌道結構整體剛度大，列車橫向荷載僅對作用點附近受力有影響，而對整體幾乎無影響。對計算結果分析可知，相同曲線半徑和曲線長度下，對鋼軌施加不同溫度荷載，對鋼軌受力突變兩側的差值幾乎沒有影響，即在同一點施加荷載工況2—工況6，計算結果基本相同。此外，計算結果表明，列車橫向荷載分別在直圓點與曲中點時，鋼軌受力突變兩側的差值基本一致。

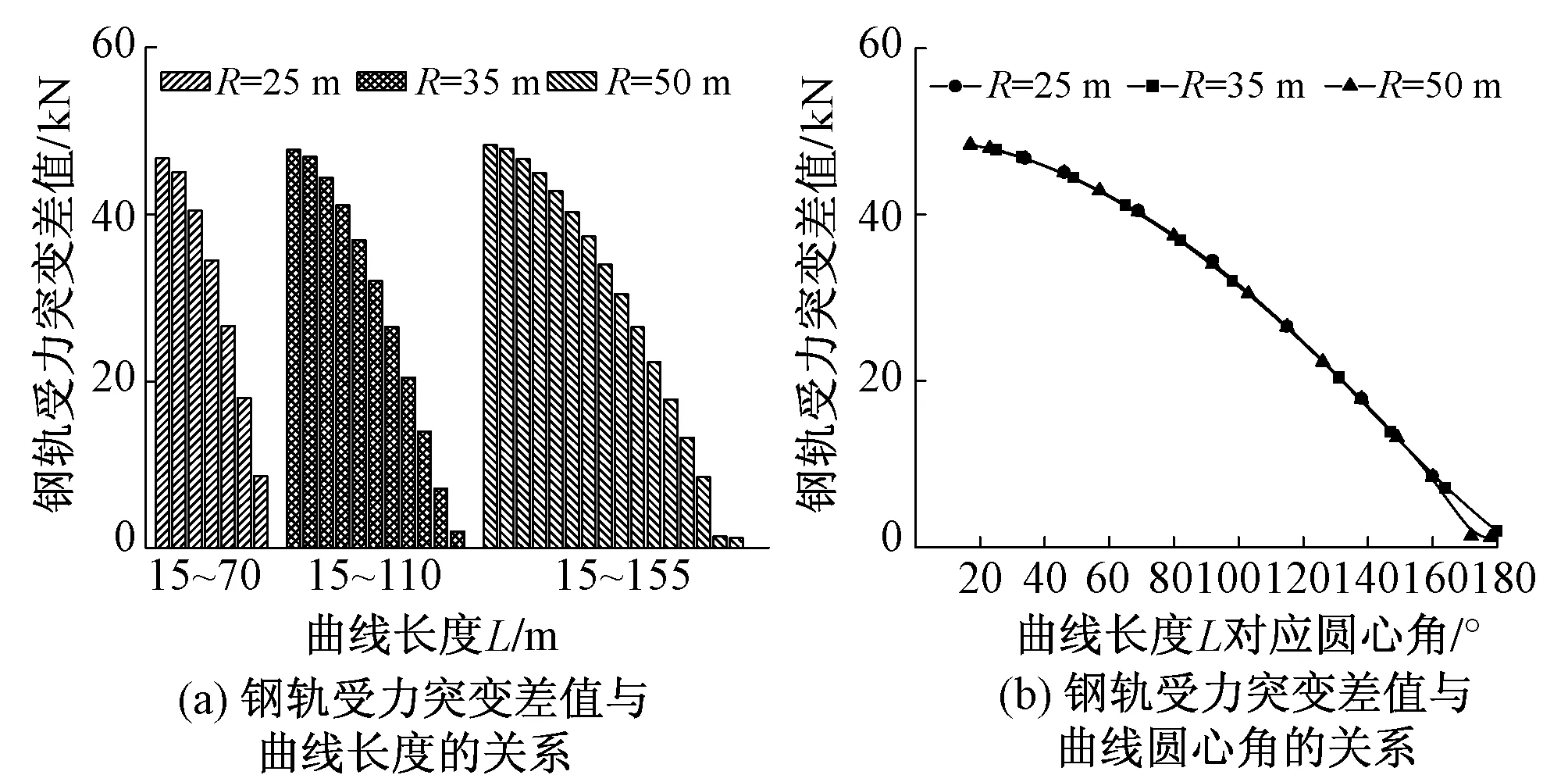
圖4 常用荷載作用下鋼軌受力突變差值

在排除鋼軌溫度、作用點等無關影響因素后，得到常用荷載組合作用時，鋼軌受力突變差值隨曲線半徑、曲線長度的變化規律，如圖4所示。由圖4(a)可知，相同曲線半徑時，鋼軌受力突變差隨曲線長度的增長而快速減小，曲線半徑為35 m時，曲線長度為 110 m 時的鋼軌受力突變差僅為曲線長度為15 m時的4%；曲線半徑為50 m時，曲線長度為155 m時的鋼軌受力突變差僅為曲線長度為15 m時的2%。由圖4(b)可知，不同曲線半徑下，鋼軌受力突變差隨著圓心角變化規律基本相同，隨著圓心角的增大，鋼軌受力突變差減小速度由慢變快，即曲線段圓弧長度對應圓心角較小時，列車橫向荷載作用對鋼軌受力影響較大，而對應圓心角較大時則影響較小，當對應圓心角達到或者接近180°時，已幾乎沒有影響。

由上述分析可知，軌道結構在常用荷載組合作用下，鋼軌在列車橫向荷載作用點兩側受力形成突變，其差值僅與曲線段圓弧長度對應圓心角有關，與鋼軌溫度、作用點、曲線半徑無關。以上計算結果基于計算假定，未考慮軌道結構出現扣件失效等病害情況。為了降低列車通過小曲線半徑時產生的橫向力對軌道結構受力和變形的影響，可選用較大的圓心角。

3 結論

本文根據有軌電車交叉路口特小曲線半徑段軌道結構特點，建立鋼軌-道床三維空間耦合力學模型，在不同荷載工況作用下，得到軌道結構的受力和變形特性，結論如下：

1)軌道結構在最大溫度荷載工況作用下，軌道結構未發生失穩破壞。小半徑曲線段軌道結構向外臌曲變形，鋼軌溫度力得到釋放。而直線段為無縫線路固定區，鋼軌溫度力無釋放，在直圓點處容易受到直線段擠壓而形成折角，其主要原因是曲率變化不連續。建議小半徑曲線地段設置緩和曲線，有利于增強無縫線路穩定性。

2)軌道結構在最大溫度荷載工況作用下，軌道結構整體橫向位移較大，在鋼軌與硬化鋪裝銜接處應采用可變形材料，以適應變形，防止擠壓破壞。

3)軌道結構在最大溫度荷載工況作用下，曲線對應圓心角小于90°時，溫度力釋放量快速增長；圓心角介于90°～150°時，溫度力釋放量增速放慢；超過150°時，溫度力釋放量出現一定的減少。

4)圓心角小于150°時，曲線半徑越小，溫度力釋放量越小，這主要是由于曲線半徑大所對應的線路長，其下部支承層為連續結構，在溫度力作用下向外膨脹變形，會帶動無縫線路橫向位移和加大無縫線路溫度力的釋放。盡管小曲線半徑對無縫線路受力和變形更有利，但會限制有軌電車允許通過速度，延長通過時間、影響交通，建議實際選線工作時，綜合考慮曲線半徑、允許通過速度、交通影響等因素。

5)軌道結構在常用荷載組合作用下，鋼軌在列車橫向荷載作用點兩側形成受力突變，其差值僅與曲線段圓弧長度對應圓心角有關，與鋼軌溫度、作用點、曲線半徑無關。為了降低列車通過小半徑曲線時產生的橫向力對軌道結構受力和變形的影響，建議選用較大的圓心角。