一種展平式彈丸擠進簡化模型仿真分析

高 巖，李 強，譚 慶

(中北大學 機電工程學院，太原 030051)

彈丸擠進過程是整個彈丸發射過程中極為重要的一個構成部分[1]。炮管內的膛線包括凸出和凹下部分，彈丸略大于膛內凸出部分所留的空間，彈丸受到膛線阻力的作用，所以擠進是緩慢的，當此阻力達到最大時，彈丸完全擠進了膛線，這個過程就是擠進過程[2]。擠進過程是一個極其復雜的過程，在經典內彈道中假設彈丸擠進時是瞬間完成的，擠進壓力假定為恒定值，但實際過程中，隨著彈底壓力的增大，彈丸開始運動，彈帶嵌入膛線而產生塑性變形，并逐步擠入身管膛內[3]。

孫全兆[4]通過對大口徑榴彈炮彈帶擠進試驗系統的構件，進行了大口徑榴彈炮彈帶擠進動力學分析研究。劉國慶[5]通過非線性有限元法建立彈/槍相互作用數值計算模型，研究槍管坡膛結構參數、線膛結構參數與外形結構參數微小變化對彈頭發射過程的影響。李宣榮[6]對高速沖擊擠進問題進行瞬態有限元分析，模擬彈丸擠進炮管的動力學過程。樊黎霞等[7]通過對彈丸擠進過程的有限元模擬與分析，得到擠進前后彈頭殼和鉛芯的變形特征，以及擠進結束后彈丸的殘余應力。曹學龍等[8]基于Hypermesh和Abaqus建立5種寬度彈帶的擠進過程有限元模型，采用載荷幅值子程序的方法，聯合求解內彈道方程組和非線性有限元過程。現有的彈丸擠進模型多為身管和彈丸未加簡化的擠進模型，從模擬的結果上看，每根膛線上的受力變形情況大體相同，所以只要知道任意一根膛線的受力變形情況就可以掌握全身管受力變形情況。對此，以12.7 mm步槍彈為研究對象，將身管和彈丸均展平，選取一根膛線進行彈丸擠進的模擬仿真。

1 彈丸擠進過程中身管受力理論分析

槍彈擠進過程中，身管各部分受力示意圖如圖1所示，纏角為η，導轉側角為α，坡膛角為β，坡膛部分受力Fp，陽線受力Ft，陰線受力Fs，導轉側受力Fd1，Fd2，則有[9]

F=Fp+Ft+Fs+Fd1+Fd2

(1)

令在接觸面上產生的接觸應力分別為σp，τp；σt，τt；σs，τs；σd1，τd1；σd2，τd2。法向力和切向力通過摩擦因數f呈比例關系，即

(2)

在槍管軸線的力為

Fz=Fpz+Ftz+Fsz+Fd1z+Fd2z

(3)

式中

2 仿真分析

2.1 建立簡化模型

身管膛線通常為對稱結構，每一根膛線各部位上的受力變形規律基本相同。隨著計算機的發展，有限元模型使用超大規模的網格進行計算成為了可能。現有的彈丸擠進模型有限元網格規模通常在30萬個以上，計算量很大。為方便計算，將彈丸和身管展平。簡化為直切(圖2)和斜切(圖3)兩種模型，在進行有限元仿真時，取一根膛線作為研究對象，可以將網格數量縮減至不到2萬個單元，大大縮小了計算量，同時保證了計算精度。

12.7 mm步槍中，彈丸外徑為13.01 mm；身管陰線直徑為13 mm，陽線直徑為12.66 mm。

令擠進長度為L，坡膛角為β，則擠除區面積

紫銅抗壓強度1 471 MPa(M態棒材)，剪切強度τ=150 MPa(M態)、210 MPa(Y態)。

斜切模型彈丸沿膛線延伸方向最大壓應力為

蘇州園區的用地在規劃時意圖明確，在宏觀上形成了具有主題的區域，如獨墅湖高教區和金雞湖商業區等，這種做法一方面將資源集中，另一方面也造成了城市層面的資源分配不合理的局面。基于TND的理論，可以通過在各個區域內的5min步行圈中設置具有一定容積率且功能豐富的“活力點”，最大程度地吸引人到各“活力點”中活動，并在“活力點”之間產生流動，以提高城市活力。

1 523 MPa與紫銅抗拉強度1 471 MPa比較接近，誤差小。

2.2 建立擠進簡化模型

彈丸擠進過程對身管武器內彈道循環有著重要影響，為了定量研究彈丸擠進身管的過程，本文選用ABAQUS有限元分析軟件對擠進過程進行了模擬，將身管(包括膛線)和彈丸均展平，結構如圖5、圖6所示。

2.3 彈丸擠進邊界條件

身管除了內膛面外，其余面均完全約束，如圖7所示。限制彈丸X軸及Z軸的自由度，對彈丸尾部施加膛壓載荷。

2.4 材料定義

該彈丸擠進研究中，身管材料為30SiMn2MoVA，其材料參數見表1。彈丸材料為F11覆銅鋼，本文采用黃銅作為彈體材料，其材料常數見表2。彈丸在坡膛擠進過程中，彈殼表面會產生塑形變形，且與膛線及身管壁面摩擦產生高溫，故采用Johnson-Cook屈服模型，該模型中屈服應力是塑形應變、應變率及溫度的函數[10]。

σ=(A+Bεpn)(1+clnε*)(1-T*m)

式中：A，B，n為材料及其應變硬化特性；c為材料應變率敏感性；m為材料溫度敏感性；σ為等效應力；εp為等效塑形應變；ε*=ε/ε0;ε為應變率；ε0為參考應變率；T*=(T-Tr)/(Tm-Tr);T為試驗溫度；Tm為材料熔化溫度；Tr為材料相對參考溫度。

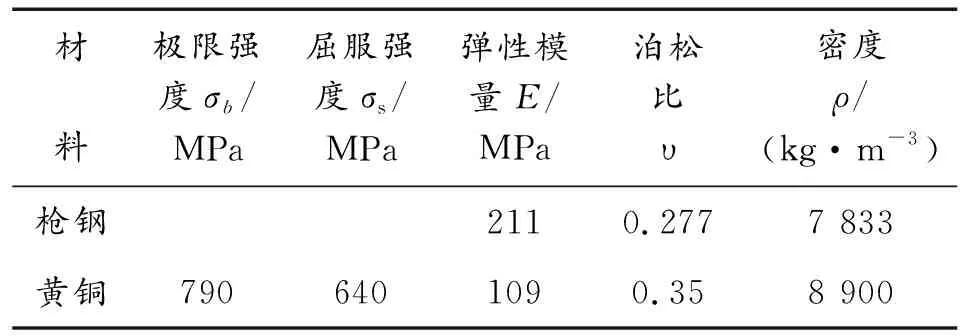
表1 黃銅材料參數

表2 黃銅Johnson-Cook模型中的材料常數

3 結果及分析

3.1 仿真結果

對仿真結果進行分析，身管膛線起始部陽線在身管壽命周期內是磨損最嚴重的部位。身管受力為陽線兩側應力大，中間小。導轉側的應力大于非導轉側應力，如圖8所示。

3.2 摩擦因數對擠進應力的影響

3.3 坡膛角度對擠進應力的影響

為研究坡膛角度對擠進應力的影響，本文選取坡膛角為0.3°、0.5°、1°、1.5°，對比坡膛中部應力與陽線中部應力，坡膛底部應力與陽線中部應力，如圖11、圖12所示。在身管材料彈塑性極限允許的范圍內，應該使坡膛角盡量的大，減少擠進時間。過小的坡膛角可能會使擠進產生類似于螺紋脫扣的現象，不能產生引導線(螺旋線)，或者產生的引導線不規則。

4 結論

1) 仿真結果表明，簡化模型的計算結果相當，計算量小，計算時間大大縮小，是一種研究彈丸擠進規律的有效方法。

2) 坡膛角度為0.5°時，彈丸完全擠入彈帶的時間為0.7 ms左右，與未加簡化的模型模擬結果相近。

3) 動摩擦因數增大會使擠進完成時間增長，但對彈丸擠進過程中身管應力場分布的影響不大。同時，摩擦因系數的增大對擠進完成后彈丸沿膛運動時身管應力增大。

4) 坡膛角度越小，擠進應力變化越平緩，有利于提高身管壽命；坡膛角為0.3°時身管膛線起始部受力較均勻。