火控雷達(dá)組合欺騙式干擾研究

張宏偉，冉宏遠(yuǎn)

(陸軍工程大學(xué) 石家莊校區(qū)，石家莊 050000)

火控雷達(dá)是現(xiàn)代防空武器系統(tǒng)的關(guān)鍵部分，其主要作用是實(shí)現(xiàn)目標(biāo)的精確跟蹤和火力控制。對(duì)火控雷達(dá)實(shí)施高強(qiáng)度、有針對(duì)性、多樣式的電磁干擾，是提高突防概率、破壞防空體系的重要手段。由于火控雷達(dá)對(duì)目標(biāo)的測(cè)量具有很高的精度，以往都是利用單部干擾機(jī)對(duì)其干擾，對(duì)火控雷達(dá)的一維或者二維參數(shù)進(jìn)行欺騙，或者直接采取壓制性干擾。但是三維參數(shù)精確化的欺騙式干擾，實(shí)現(xiàn)相對(duì)困難。隨著現(xiàn)代戰(zhàn)爭(zhēng)中的電磁環(huán)境越來(lái)越復(fù)雜，飛機(jī)的作戰(zhàn)水平和生存能力需要大大提高，本文的應(yīng)用背景是飛機(jī)兩機(jī)翼上各搭載一部干擾機(jī)，對(duì)單脈沖火控雷達(dá)實(shí)施三維參數(shù)的欺騙式干擾。

1 火控雷達(dá)干擾分析

1.1 火控雷達(dá)實(shí)施干擾的特殊性

對(duì)于雷達(dá)的干擾樣式主要有遮蓋式干擾和欺騙式干擾。遮蓋式干擾是利用噪聲或類似噪聲的干擾信號(hào)或壓制回波信號(hào)，在雷達(dá)顯示器上形成強(qiáng)雜波背景或大量假目標(biāo)回波，使雷達(dá)的探測(cè)能力降低，此類干擾樣式主要應(yīng)用于干擾搜索和引導(dǎo)雷達(dá)；欺騙式干擾是采用假的目標(biāo)或目標(biāo)信息作用于雷達(dá)的目標(biāo)參數(shù)、參數(shù)測(cè)量和跟蹤系統(tǒng)，使雷達(dá)發(fā)生嚴(yán)重的虛警，或者不能正確地測(cè)量和跟蹤目標(biāo)參數(shù)，欺騙樣式主要有角度、距離、速度和假目標(biāo)欺騙等，欺騙式干擾主要應(yīng)用于干擾火控雷達(dá)。

1) 最大信號(hào)法測(cè)角系統(tǒng)。該測(cè)角方法精度不高，不能用于自動(dòng)測(cè)角，在搜索和引導(dǎo)雷達(dá)中應(yīng)用較為廣泛；

2) 圓錐掃描自動(dòng)測(cè)角系統(tǒng)。該測(cè)角方法可以通過(guò)對(duì)信號(hào)導(dǎo)相的方法來(lái)實(shí)現(xiàn)角度欺騙，但是目前這種測(cè)角系統(tǒng)的雷達(dá)并不多見(jiàn)，而且測(cè)角精度不高。

3) 單脈沖自動(dòng)測(cè)角系統(tǒng)。該測(cè)角方法目前廣泛應(yīng)用于火控雷達(dá)中。單脈沖自動(dòng)測(cè)角系統(tǒng)具有測(cè)角速度快，測(cè)角精度高等特點(diǎn)，而且不易被干擾。目前，利用單個(gè)干擾機(jī)對(duì)單脈沖測(cè)角系統(tǒng)實(shí)施精確化的角度欺騙難度較大，利用雙干擾機(jī)的密切配合，才會(huì)產(chǎn)生精確化的角度欺騙[1]。

1.2 針對(duì)火控雷達(dá)的常用干擾策略

1) 角度欺騙干擾

反向交叉眼技術(shù)是利用雙干擾機(jī)的功率和雙信號(hào)的相位不同，對(duì)單脈沖雷達(dá)的測(cè)角系統(tǒng)實(shí)施欺騙[2]，如圖1所示。

θ為雷達(dá)測(cè)得的角度與真實(shí)目標(biāo)角度的差值，G1和G2分別為雙干擾機(jī)發(fā)射信號(hào)增益，θe為雷達(dá)與雙干擾機(jī)中部連線和雷達(dá)與干擾機(jī)連線的夾角，Δθ為雙干擾機(jī)與雷達(dá)連線的夾角，Δφ為天線2發(fā)射信號(hào)相位改變量，L為雙干擾機(jī)之間的距離，R為雙干擾機(jī)中部連線距離雷達(dá)距離，β=G2/G1，Δθ=2θe。

依據(jù)文獻(xiàn)[2]得：

(1)

對(duì)式(1)仿真可得如圖2所示。

取Δφ=180°，進(jìn)行有規(guī)律的變化β，可以產(chǎn)生角度欺騙。

2) 距離欺騙干擾

雷達(dá)距離欺騙干擾的工作基本原理為干擾機(jī)接收雷達(dá)信號(hào)，對(duì)雷達(dá)信號(hào)進(jìn)行有規(guī)律的延時(shí)，再由干擾機(jī)發(fā)出[3]。

3) 速度欺騙干擾

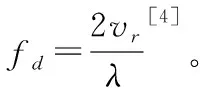
以上的干擾分析都是基于欺騙火控雷達(dá)單維目標(biāo)參數(shù)的，部分干擾機(jī)也有把距離-速度組合進(jìn)行同時(shí)欺騙的[5]。如果單獨(dú)實(shí)施距離欺騙、速度欺騙或者距離-速度組合欺騙，虛假目標(biāo)的角度沒(méi)有改變，火力一旦實(shí)施射擊，目標(biāo)仍有被擊中的可能性。如果單獨(dú)實(shí)施角度欺騙，假目標(biāo)就有一個(gè)角度信息是錯(cuò)誤信息，不利于保護(hù)真實(shí)目標(biāo)[6]。

針對(duì)以上分析的當(dāng)前干擾策略的不足，本文提出了一種距離-速度-角度三維參數(shù)的組合欺騙式干擾的實(shí)現(xiàn)方法，利用該方法可以更好的對(duì)火控雷達(dá)實(shí)施欺騙式干擾，更有利于保護(hù)真實(shí)目標(biāo)。

2 三維參數(shù)組合欺騙式干擾數(shù)學(xué)建模

對(duì)距離-速度-角度三維參數(shù)的組合欺騙式干擾建立數(shù)學(xué)模型時(shí)，為了便于分析，按照先分解，后結(jié)合的思路進(jìn)行。首先對(duì)距離-速度二維參數(shù)欺騙干擾進(jìn)行建模，用該模型和角度欺騙模型進(jìn)行有機(jī)組合，完成三維參數(shù)的組合欺騙式干擾數(shù)學(xué)建模。

2.1 二維參數(shù)組合欺騙式干擾數(shù)學(xué)建模

干擾機(jī)對(duì)截獲的雷達(dá)信號(hào)進(jìn)行延時(shí)處理，每隔Tj的時(shí)間對(duì)信號(hào)進(jìn)行一次延時(shí)改變，每隔Tj的延時(shí)改變量為tj，tj為延時(shí)步進(jìn)步長(zhǎng)，Tj為步進(jìn)時(shí)間間隔，fj為在Tj時(shí)間內(nèi)對(duì)轉(zhuǎn)發(fā)信號(hào)的固定頻率量，vj為假目標(biāo)相對(duì)于真實(shí)目標(biāo)的速度[7]。

則有下式成立：

(2)

對(duì)雷達(dá)信號(hào)在時(shí)域內(nèi)和頻域內(nèi)進(jìn)行調(diào)制時(shí)，Tj、tj、fj需要滿足以下關(guān)系：

(3)

將式(2)式代入式(3)式可得：

(4)

雷達(dá)信號(hào)的載波頻率為f0。

距離-速度組合欺騙干擾過(guò)程實(shí)現(xiàn)過(guò)程：每隔Tj的時(shí)間段，對(duì)信號(hào)進(jìn)行一次延遲處理，延時(shí)量為tj,則，第m次步進(jìn)延時(shí)時(shí)，現(xiàn)實(shí)真實(shí)的時(shí)間為m×Tj，信號(hào)的延遲量為m×tj，在頻域內(nèi)，對(duì)信號(hào)的多普勒頻率的變化量為fj[8]，如圖3所示。

在二維參數(shù)組合欺騙式干擾模型基礎(chǔ)上，融合角度欺騙理論，建立三維參數(shù)組合干擾建模。其原理為：對(duì)信號(hào)進(jìn)行時(shí)間延遲，產(chǎn)生距離欺騙；多普勒頻率改變，產(chǎn)生速度欺騙，同時(shí)調(diào)整雙干擾信號(hào)的相位和功率(本文統(tǒng)一規(guī)定一路信號(hào)相位調(diào)整180°，另一路信號(hào)相位不變)，產(chǎn)生角度欺騙[9]

2.2 距離-速度-角度三維參數(shù)組合欺騙式干擾數(shù)學(xué)建模

飛機(jī)以航路捷徑為0 m，高度不變的姿態(tài)，勻速水平飛向雷達(dá)。想要獲得一個(gè)與真實(shí)目標(biāo)速度有角度偏差的虛假速度，則首先需要對(duì)假目標(biāo)速度進(jìn)行分解。

如圖4所示，假目標(biāo)速度分解為兩個(gè)速度分量，徑向速度v1，切向速度v2。

徑向速度可以依據(jù)式(4)分析，利用距離-速度欺騙干擾實(shí)現(xiàn)方法產(chǎn)生。切向速度可利用式(1)，改變?chǔ)轮担a(chǎn)生虛假勻速[10]。

若虛假目標(biāo)勻速分行，則徑向速度v1和切向速度v2均為恒值。如圖5所示。

v1為恒值，則滿足式(4)即可；tj為延時(shí)步進(jìn)步長(zhǎng)，Tj為步進(jìn)時(shí)間間隔，即在時(shí)域內(nèi)對(duì)雷達(dá)信號(hào)進(jìn)行延時(shí)處理時(shí)，每隔Tj的時(shí)間對(duì)數(shù)字信號(hào)進(jìn)行一次延時(shí)改變，每隔Tj的延時(shí)改變量為tj；fj為在Tj時(shí)間內(nèi)對(duì)轉(zhuǎn)發(fā)信號(hào)的固定頻率量；每隔Tj時(shí)間，虛假目標(biāo)在徑向上飛出的距離都是相等的，即

s1=s2=s3…=sk

同時(shí)v2也為恒值，每隔Tj時(shí)間，虛假目標(biāo)在切向上飛出的距離都是相等的，即

l1=l2=l3…=lk

若要保持上式相等，依據(jù)反向交叉眼原理分析可知，每隔Tj的時(shí)間，產(chǎn)生的虛假角度變化量是不一樣的，即：

α1≠α2≠α3…≠αk

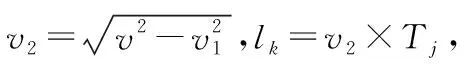
Rk=R0+(v1-v3)TjK

則有下式成立：

θk為β經(jīng)歷過(guò)K次變化后，產(chǎn)生的欺騙角度。

由式(1)得：

(5)

Δθk為雙干擾機(jī)與雷達(dá)之間的夾角，L為雙干擾機(jī)源之間的距離，第K次對(duì)信號(hào)延時(shí)，飛機(jī)距離雷達(dá)的距離為R0-v3TjK

(6)

將(5)式代入(6)式化簡(jiǎn)得

(7)

因此，若要滿足距離-速度-角度三維參數(shù)的組合欺騙式干擾，則需要建立以下數(shù)學(xué)模型：

(8)

3 三維參數(shù)組合欺騙式干擾仿真分析

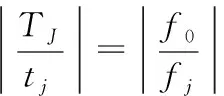
當(dāng)延時(shí)步進(jìn)時(shí)長(zhǎng)tj為定值(40 ns)時(shí)，對(duì)轉(zhuǎn)發(fā)信號(hào)的多普勒頻率改變量越大，則需要的步進(jìn)時(shí)間間隔Tj越小，二者成反比。

當(dāng)取干擾信號(hào)頻移量fj為4 kHz時(shí)，步進(jìn)時(shí)間間隔Tj為40 ms，并且延時(shí)步進(jìn)時(shí)長(zhǎng)tj為40 ns。此時(shí)，對(duì)式(8)中的前3個(gè)等式進(jìn)行仿真，得出β的數(shù)值大小(表1)。

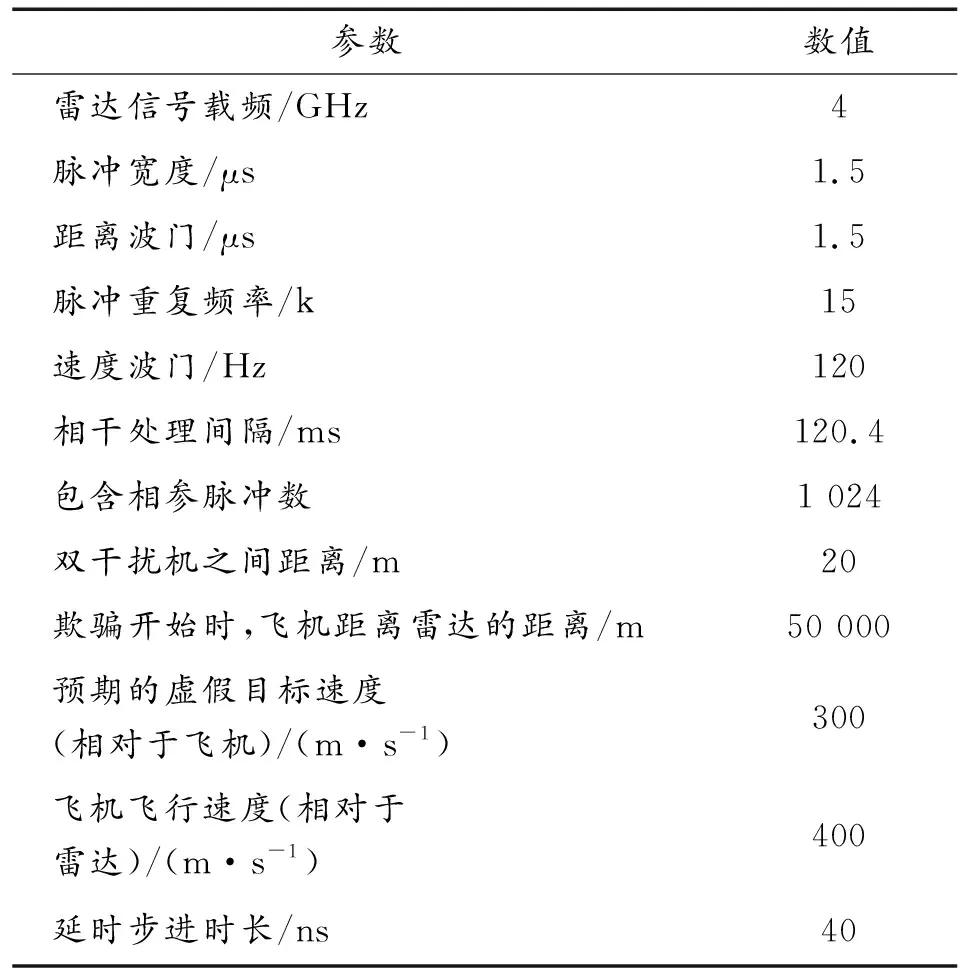
表1 仿真參數(shù)

如圖6所示：對(duì)距離-速度-角度三維參數(shù)組合欺騙式干擾的實(shí)現(xiàn)過(guò)程描述如下：飛機(jī)雙機(jī)翼上各搭載一部干擾機(jī)，對(duì)火控雷達(dá)實(shí)施干擾。干擾開始后，信號(hào)逐次步進(jìn)，每次步進(jìn)時(shí)，信號(hào)頻移量fj為4 kHz(該數(shù)值為恒定值，步進(jìn)過(guò)程中不累加)，步進(jìn)時(shí)間間隔Tj為40 ms，延時(shí)步進(jìn)時(shí)長(zhǎng)tj為40 ns(該數(shù)值為累加值，每步進(jìn)一次，延時(shí)累加一次)，根據(jù)步進(jìn)次數(shù)的不同，雙干擾機(jī)功率比β是不同的，具體β的數(shù)值可由式(8)計(jì)算得出，圖7為信號(hào)步進(jìn)間隔次數(shù)與相應(yīng)步進(jìn)次數(shù)β值的仿真圖。

對(duì)式(8)的Δβk進(jìn)行分析

Δβk=βk-βk-1

(9)

對(duì)式(9)仿真可得圖8所示的結(jié)果。

由圖8可知，隨著步進(jìn)次數(shù)的增加，每次β的變化量越來(lái)越小。由式(3)得：虛假目標(biāo)相對(duì)于飛機(jī)在徑向上的速度分量v1=150 m/s，虛假目標(biāo)相對(duì)于飛機(jī)的速度v=300 m/s。圖9為距離-速度-角度三維參數(shù)組合欺騙式干擾的示意圖。概略描述了真實(shí)目標(biāo)、虛假目標(biāo)和雷達(dá)的相對(duì)關(guān)系。

假目標(biāo)距離-速度-角度三維參數(shù)的組合欺騙式可成功實(shí)現(xiàn)，在等步進(jìn)時(shí)間間隔下，對(duì)信號(hào)進(jìn)行等量延遲，每次步進(jìn)時(shí)，兩干擾機(jī)的功率比是變化的，并且功率比的變化量越來(lái)越小，在干擾全程對(duì)信號(hào)多普勒頻率的改變量為恒定值。

4 結(jié)論

基于單維參數(shù)的欺騙式干擾理論，對(duì)火控雷達(dá)實(shí)施距離-速度二維參數(shù)欺騙式干擾實(shí)現(xiàn)較為容易，對(duì)于距離-速度-角度的三維參數(shù)欺騙式干擾實(shí)現(xiàn)相對(duì)復(fù)雜。通過(guò)研究論證分析，得出具體實(shí)現(xiàn)方法。