淺談轉化技術在高考數學“選考題”中的應用

郭崇泉(深圳市平岡中學 廣東 深圳 518116)

從2016年開始，廣東考生面臨著由廣東卷向全國卷高考轉變，尤其文科高考數學從2017年開始，試題中選考題組由之前的“三選一”改為“二選一”，去掉了幾何證明題組，這讓很多“吃老本”的同學舉頭無措，也因此出現了各種的不適應，對于全國卷的選考題第(2)問普遍感覺就是難，做題無從下手，很難拿到滿分。其實，全國卷的選考題組命題特點是突出對主干知識的考查，設計合理、梯度適中，知識點相互滲透，嚴格遵循“在考查數學知識和技能的同時，著重對考生運用知識和技能，分析和解決問題的能力進行考查，加強對考生實踐能力和創新精神的考查”的命題原則，考核內容緊扣教材，嚴從學綱，重視應用。學生覺得全國卷的選考題組難，往往是沒有立足基礎，從基礎知識中找出源頭，去理解和分析題型，從而進行等價轉化。針對以上情況，筆者將采用實例闡明轉化技術在高考數學“選考題”中的應用。所謂的轉化技術是一項以學生立場為原則，通過結構化、簡潔化、可視化、通俗化、活動化等方式化生為熟、化繁為簡、化難為易，使一些生題、難題、難理解的知識點轉化為學生能理解、能接受、能掌握的知識和技能。

1 轉化技術之一——化生為熟

【案例1】極坐標、參數方程及不等式選講等內容是高考的必考內容，并且是高考固定的第22，23題，其內容在整個高中數學中相對比較獨立且新穎，致使讓許多學生“望題卻步”。化生為熟是學生最常采用的一種解題方式，即從熟悉的內容入手，快速找到解決生題的竅門。

例:(2017全國I)23．［選修4—5:不等式選講］(10分)

已知函數f(x)=–x2+ax+4，g(x)=│x+1│+│x–1│．

(1)當a=1時，求不等式f(x)≥g(x)的解集;

(2)若不等式f(x)≥g(x)的解集包含［–1，1］，求a的取值范圍．

當學生剛接觸這道題時，第(1)問很容易解決，但第(2)問簡直是無從下手，不知所以云，難點在于不等式解集包含”這句話的理解上，之前很少碰到過這樣的案例，于是很多同學就開始亂寫了。其實這道題并沒有想象中這么難，只需通過轉化技術－－化生為熟，轉化成“恒成立”熟悉的問題，就能很快得到解決。

【解析】(1)當a=1時，不等式f(x)≥g(x)等價于x2－x+－4≤0．①

當x＜－1時，①式化為x2－3x－4≤0，無解，

當 －1≤x≤1時，①式化為 x2－x－2≤0，從而 －1≤x≤1，

當x＞1時，①式化為 x2+x－4≤0，從而1＜x≤

( 2 )由第( 1 )知:當x∈ [ －1，1 ]時，g(x)=2，

所以f(x)≥g(x)的解集包含 [ －1，1]，等價于當 x∈ [ －1，1]時f(x)≥2恒成立，

即x2－ax－2≤0，對x∈ [ －1，1]成立，設h(x)=x2－ax－2，

2 轉化技術之二——化繁為簡

【案例2】俗話說:“簡單到極致就是精彩。”高中數學的知識點多而散，造成學生在記憶和運用時總是“張冠李戴”。通過“簡潔化技術”可以把散亂的知識點轉化成為容易理解、運用方便的解題工具，能很好地幫助學生正確運用相關知識，只有這樣才能把復雜問題簡單化，快速、正確的找到解決問題的辦法。

例:(2017全國I)22．［選修4―4:坐標系與參數方程］(10分)

(1)若a=?1，求C與l的交點坐標;

高考分析:專家說，學生解答這道題，第(1)問基本上都能得到分，但第(2)問很難得到滿分。筆者認為之所以學生第(2)問不能拿到滿分，主要是因為選擇方法不恰當或計算能力不過關等原因造成的，對大多數學生而言，他們會選擇曲線C橢圓的直角坐標方程與直線的直角坐標方程聯立求解，這種方法數學思想簡單，但解題過程繁瑣且復雜，在高考緊張數學考試中，不是一個好的選擇。若學生掌握轉化技術——簡潔化的話，把曲線上的點到直線的距離問題轉化為三角函數求最值問題，化繁為簡，那么這個問題就會很快的解決。

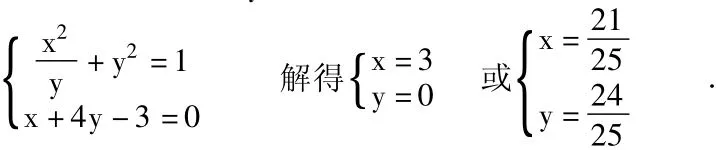
(2)L的普通方程為x+4y－a－4=0，

設曲線C上任一點為P ( 3 cosθ，sin θ)，

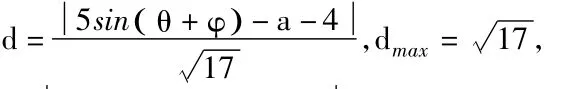
當sin ( θ+φ)=1時最大，即5－a－4=17，a=－16，

當sin ( θ +φ ) =－1時最大，即a+9=17，a=8，

綜上:a=－16或a=8．

萬事都有髓，把握其精髓，復雜問題可以變得很簡單。

3 轉化技術之三——化難為易

【案例3】在高中數學教學中，我們常常會遇到一些復雜知識、抽象知識等，學生很難簡單直觀理解，這就要求我們把它轉化為學生能理解、能接受、能掌握的知識(技能)。而在數學教學中常常采用數形結合法、分類討論法、反證分析法、賦值法、排除法、多媒體演示等方法，化難為易，不僅便于學生的學習，還有利于培養學生科學的思維邏輯辨析能力。例如在講解極坐標與參數方程內容時，對于極坐標、參數方程的概念及方程等知識點比較抽象難懂，筆者在教學中用直角坐標方程、極坐標方程及參數方程表示同一個圖形，讓學生找出他們的異同點，總結優缺點，從中感受從抽象到具體的學習過程。

例:(2014全國I)23．［選修4―4:坐標系與參數方程］(10分)

(1)寫出曲線a，b的參數方程，直線2a+3b=6的普通方程;

(2)過曲線C上任意一點P作與l夾角為30°的直線，交l于點A，求的最大值與最小值．

在2014年高考選考題中，選考這道題的學生第(2)問基本不得分，筆者分析這道題的難點在“過曲線C上任意一點P作與l夾角為30°的直線”這句話的理解上，學生不能把這句話轉化成等價的數學問題，不能化難為易，進而得不到應有的分數。而這個問題只需要利用數形結合的轉化思想，就能輕而易舉的解決。

直線l的普通方程為2x+y－6=0．

(2)曲線 C上任意一點 p(2cosθ，3sinθ)到 l的距離為 d=

高質量學習理論中的轉化技術是一種很實用，很有效的理論方法，它是把未知解的問題轉化到在已有知識范圍內可解的問題的一種重要的解題技術．通過不斷的轉化，把不熟悉、不規范、復雜的問題轉化為熟悉、規范甚至模式法、簡單的問題．通常有"數"與"形"的相互轉化、一般與特殊互化、生疏問題向熟悉問題轉化、實際問題轉化為數學問題等，本文通過例題講述轉化思想在高中數學中的解題應用，并說明這種思想解題的有效性與優越性。