階梯流作用下長柔立管渦激振動行波效應研究

白 旭，樂智斌

（江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江212003）

0 引 言

深水立管是連接海底井口與海面作業平臺的關鍵設備。在復雜的海洋環境中，由海流引起的渦激振動（VIV）是造成立管發生疲勞破壞的主要因素[1]。

由于深水立管具有大長細比等特點，其渦激振動響應呈現出非線性特征，與剛性圓柱體存在較大差異。Bourguet等[2]通過水池試驗發現長柔結構物發生渦激振動時在順流向存在十分顯著的響應，并指出在高質量比下單自由度和雙自由度渦激振動差距較小，而低質量比條件下順流向的振動被激發無法忽略。因此可以認為在低質量比條件下對海洋長柔立管進行渦激振動響應分析時，必須考慮順流向的影響。對此，唐國強等[3]進行了長細比為1750的柔性桿件渦激振動實驗，發現順流向的振動頻率和振動模態數均為橫向的2倍。Gao等[4]通過實驗對比剪切流和均勻流作用下加設了抑制振動裝置的立管，發現在均勻流時立管會產生比剪切流下更高的振動頻率。林琳等[5]通過莫里森方程計算順流力，建立了三維柔性立管的雙自由度渦激動力響應方程，發現剪切流作用下隨著流速的增加，立管模態數逐漸增加。郭海燕等[6]利用功能原理建立了立管渦激振動響應數值模型，采用Newmark-β方法在時域內迭代求解其動力響應，并與實驗進行對比后得到一種能夠預測大長細比海洋立管渦激振動模態和振幅極值點的計算模型。Wang等[7]同樣發現了剪切流作用下立管的模態數與流速之間的關系，也發現剪切流的振動頻率小于均勻流，并指出在順流向會出現3倍于橫向的振動頻率。宋磊健等[8]、高云等[9]通過進行三維立管模型的實驗發現在剪切流下，其阻力系數等也與均勻流存在較大差異，在剪切流下橫向振動存在一個頻率鎖定區域，而順流向則存在兩個頻率鎖定區域，且響應隨著約化速度出現上升—下降—再上升—再下降的趨勢。

行波效應是振動響應在空間和時間上同時發生變化的振動現象，針對立管的行波效應現象，國內外學者通過柔性立管渦激振動實驗進行了大量分析。Chaplin等[10]在實驗室條件下進行了階梯狀來流，均勻流和線性剪切流的海洋立管渦激振動實驗，實驗中均發現了顯著的順流向振動，盡管數據顯示順流向振動的幅值相對橫向較小，但是其激發了更高階的模態，行波效應明顯。Jaiswal[11]在墨西哥灣進行的實驗測量以實時的流速模擬剪切流對立管的影響，發現行波效應，并總結得到行波效應從高約化速度區域向低約化速度區域傳播的結論。Bourguet等[12]對線性剪切流進行了大量的數值計算，發現剪切流和均勻流作用下，具有行波效應的區域與其他區域有著不同的運動軌跡，通過對相位的分析，發現在頻率鎖定區域相位均小于180°。羅冬冬等[13]通過CFD計算剪切流作用下的柔性隔水管發現最大位移所在位置會發生向上移動的現象，同樣也說明了行波效應的存在。

長柔立管的渦激振動在發生高模態振動情況下會出現行波效應，即結構的振動響應幅值隨著軸向會出現一個有規律的波動，特別是在考慮順流向振動時，發生的振動頻率變得更高，所激發的模態也變得更高，行波效應變得更為明顯。對于行波效應而言，其結構振動響應特性和導致的疲勞分布規律與駐波效應有明顯的區別。傳統的渦激振動預報方法對于駐波效應有效，而對于行波效應占主導的高模態數長細柔彈性體渦激振動，模態疊加法只能對有限數量的非共振模態進行分析和計算，無法體現長柔立管在考慮順流向振動的雙自由度渦激振動響應特性。由于頻域預報模型在預報大長徑比長柔立管時會受到行波效應的影響，采用時域預報模型會更有優勢，同時也為了更好地研究渦激振動中的流體作用力，大量國內外學者通過建立力分解模型和尾流振子模型得到一系列預報模型。2004年，Facchinetti[14]提出的單自由度渦激振動耦合振子模型能夠很好地模擬渦激振動運動響應，充分研究了結構和流體振子的耦合作用，分別對位移、速度、加速度三種耦合形式進行了對比和討論，該方法引起大量學者的研究和補充。Bai等[15]通過將尾流振子模型擴展到雙自由度形式，研究了該模型在雙自由度即順流向和順流向發生運動時的相位角和軌跡的關系。

時域預報模型能夠更好地對深水海洋立管的渦激振動進行預報，由于長柔立管在渦激振動時因行波效應會引起疲勞點的轉移，在進行運動響應預報和疲勞壽命計算時時域預報模型具有更大的優勢。而尾流振子模型更好地詮釋了雙向流固耦合的內涵，屬于一種最適合用以描述渦激振動這一類典型的自激振動。因此采用尾流振子模型進行時域預報模型的建立以分析深海長柔立管的渦激振動現象具有重要的工程價值和研究意義。因此本文以離散點渦法為基礎，建立三維的尾流振子計算時域模型，分析獲得階梯流作用下長柔立管的渦激振動響應特征參數，探索階梯流作用下長柔立管渦激振動行波效應機理。

1 長柔立管渦激振動模型

1.1 三維柔性立管雙自由度耦合方程

海洋立管長徑比通常大于一百，甚至有些達到千量級，故將立管看成具有柔性能夠發生變形的長細柔性桿處理，建立三維立管渦激振動物理模型如圖1所示。

除受到作用在截面的來流外，立管結構還受到尾渦引起的順流向和橫向的渦致作用力，因此可以將立管力學問題整體簡化為長細柔性梁的復雜彎曲問題。以橫向的振動為例，取立管沿高度方向的一個微段dz，如圖2進行分析。

通過力矩平衡方程和變形幾何關系可以得到如下表達式：

其中：M為梁端面的彎矩，E為立管材料的彈性模量，I為立管的截面慣性矩，Fs為截面剪切力，Y為微段的橫向振幅。 F （ y，z， ）t為流體作用力，假定每一微段為剛性體（自身不發生形變），兩端彈性支撐，可得到物理模型如圖3所示。

根據文獻[15]，可以得到尾流振子模型的雙向流體作用力表達式：

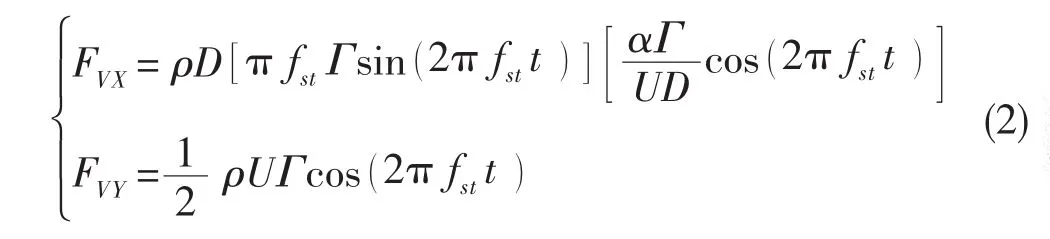
其中：D為圓柱直徑；fst為系統瀉渦頻率；α為與脈動拖曳力、斯特拉哈爾數、脈動升力系數相關的無量綱參數。

考慮到立管在軸向受到拉力作用，依據軸向的平衡方程，結合d2Y/dz2=M/EI可以得到：

擴展到順流向，結合公式（1）、（2）和（3）并無量綱化，得到基于歐拉—伯努利梁假定成立的長柔立管雙自由度渦激振動方程：

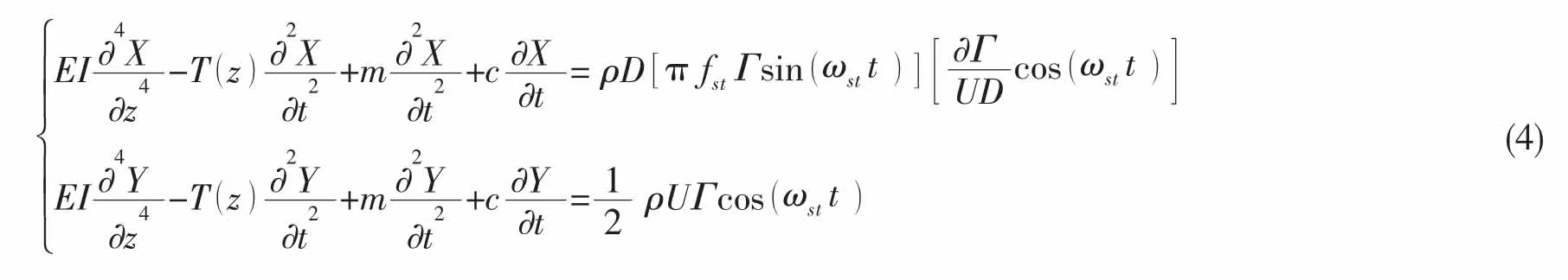
假設隨著水深的增加，立管截面、質量和阻尼均沒有變化，但軸向拉力需要考慮自身的重力作用。當立管所在流域不是均勻來流而是隨著水深變化存在有階梯的水流時，等式右邊的載荷也隨之變化。

根據文獻[16]，結構在流體通過時的振動可以用離散分布的非線性范德波爾振子模型來描述：

其中：ε是范德波爾方程耦合參數，vd是耗散參數，Fd是流體作用在結構上的載荷項即流固耦合作用力，ωst=2πStU/D是流體瀉渦頻率，與流速以及斯特勞哈爾數有關。對于耗散項vd?3q/（?z2?）t，當結構整體進行離散化處理時，只要沿著軸向劃分足夠多節點，可以認為單個單元的?2q/?z2=0。因此三維流體振子方程可以表達為：

假設結構的截面沿著軸向均是相同的形狀與大小，截面慣性矩不隨軸向發生變化，立管截面慣性矩取I；由于立管軸向拉力隨著水深而變化，T（）z為沿著軸向分布的軸向拉力。綜合以上討論，結合（4）式和（6）式可以得到三維雙自由度長柔立管渦激振動耦合模型如（7）式，式中N、M和H均為水動力參數[15]。

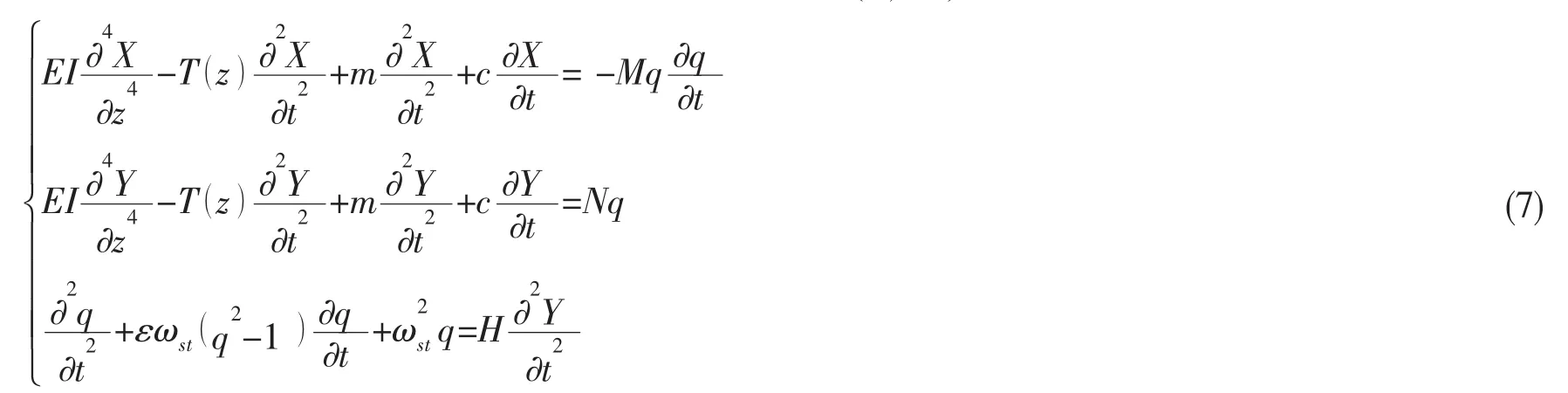
1.2 模型驗證

針對海洋環境中真實存在的階梯流，Chaplin進行了經典的階梯流實驗，將一根13.12 m的圓柱立管放置于套管中隨拖車運動，由于套管中水靜止，以此模擬海洋中洋流發生階梯性變化的實際工況[10]。該實驗所用模型參數如表1所示。

表1 Chaplin試驗參數Tab.1 Test parameters of Chaplin

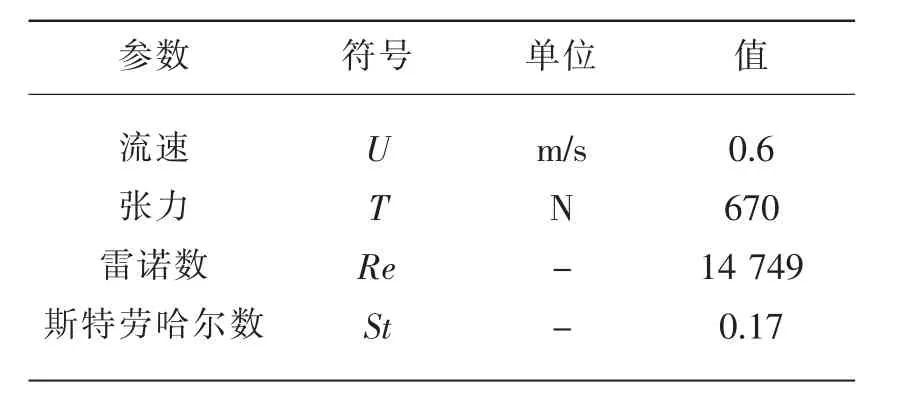
表2 驗證工況Tab.2 Verification condition

為驗證（7）式的正確性，選取Chaplin一組工況進行對比驗證，所選工況參數如表2所示。最大流速為0.6 m/s，立管下方45%部分受到流速影響，其他部分為靜水作用，僅受到濕重影響，由于結構總長為13.12 m，對0～5.9 m段施加水流進行計算。

得到載荷與實驗結果對比如圖4所示，依次為橫向振幅的包絡線對比圖、橫向振幅的標準方差對比圖和順流向振幅標準方差對比圖。結果表明：在流速為0.6 m/s下，該立管出現6階模態。沿立管高度方向振幅一致，對比立管上方的振幅，本文模型較實驗結果略大是因為在實驗中邊界進行鉸接，仍然存在一定的阻尼；另一方面，套管內徑較小，與下方置于水池的流域相比，對立管振動具有更大的阻礙，因此立管上部分的實驗結果較下部分更小，同時也小于模型結果。兩個自由度的振幅標準方差結果對比也基本一致，實驗和模型計算結果在同樣的位置出現，橫向振動被激發6階模態，順流向被激發11階模態，順流向模態數大致為橫向的2倍。通過對比Chaplin的實驗結果與（7）式的計算結果，本文提出的計算模型和方法能夠有效地對立管在階梯流下的運動響應進行預報。

2 階梯流作用下長柔立管渦激振動響應特性

不同的海洋環境中，存在多種來流形式，根據成因可以分為潮流、風海流、階梯流、熱鹽環流和波浪流等，隨時間變化可以分為周期流、定常流和瞬時流等。由于海洋環境復雜，立管的工作條件惡劣，會出現大量的未知載荷。而立管在不同的流動形式下振動響應存在著巨大的差異，本文針對階梯流，采用提出的模型對長柔立管進行渦激振動特性分析。

2.1 長柔立管渦激振動的振幅分析

設定流速U范圍為0.2～5 m/s，雷諾數范圍為2458～12290。模型總長13.12 m，進行200等分，共得到201個節點，流動形式如圖5所示，具體工況參數見表3。

表3 階梯流計算工況Tab.3 Working condition

模型計算得到所有工況下的響應后，為了說明該程序在時域上計算的穩定性和可行性。針對階梯流在低流速U=0.2 m/s下，選取L/4，L/2，3L/4處的計算結果繪制雙向無量綱振幅時程曲線，如圖6所示。可以發現：在階梯流作用下，無量綱橫向振幅最大值發生在L/4處，為1.04。

續表3

繪制階梯流在流速U=0.2 m/s下穩定后的截面運動軌跡，如圖7所示。從圖中可以看出：階梯來流作用下，橫向振幅的截面形狀不存在節點，激發2階模態，順流向振幅的截面形狀存在1個節點，激發3階模態。

2.2 長柔立管渦激振動頻率分析

長柔立管的壽命除了受到振幅的影響外，發生長時間的高頻率振動也是其疲勞破壞的重要因素之一。對于二維剛性圓柱的振動，大量學者通過實驗得到順流向振動頻率為橫向振動頻率的2倍。對于長柔立管而言，振幅較剛性圓柱更大，因此其振動頻率的研究更為重要。

通過傅里葉變換對表3中所有工況的計算結果進行頻率分析，選取L/4、L/2和3L/4處隨時間變化的振幅進行分析得到如圖8所示的無量綱幅頻曲線。對比幅頻曲線，可以看出，隨著流速的增加，主頻率增加。主頻率隨流速的變化趨勢如圖9所示。

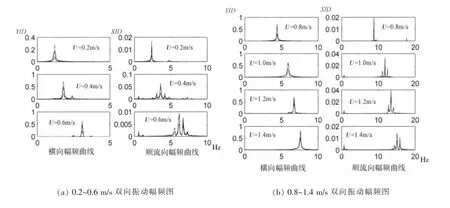
橫流向和順流向振動的主頻率與流速之間呈現出線性的關系，用fCF_main和fIL_main分別代表橫向振動主頻率和順流向振動主頻率，則可以得到fCF_main=5U及fIL_main=10U的表達式。以上分析均基于50號節點、100號節點和150節點的振動結果，為了更進一步研究立管上所有節點的振動頻率與流速之間的關系，取低流速0.8 m/s以及高流速2 m/s進一步分析振動幅頻圖譜，如圖10～11所示，可以看出亦滿足上述的規律。

3 行波效應與傳遞特性

根據Jaiswal[11]發現的行波效應可以認為順流向的高階振頻是引起行波效應的原因之一，為了更深入地研究不同流速下階梯流行波效應在橫向及順流向上的傳播規律，對表3中的0.2 m/s，0.4 m/s和2 m/s三種工況進行行波特性分析。從圖12中可以發現隨著流速的增加，會激發更高的模態數，橫向振幅最大發生在0.4 m/s的階梯流時。

文獻[17]發現長柔立管在發生渦激振動時沿軸向變化的流體作用力波動區域即為頻率鎖定區域，同時該區域的相位穩定在180°以下，表現為運動軌跡為CC（counter clockwise）方向。文獻[8]中給出了C模式（當橫向運動達到最大值時，立管運動方向與來流方向相反，為順時針）和CC模式（當橫向運動達到最大值時，立管運動方向與來流方向相同，為逆時針），如圖13所示。

當立管的橫向運動達到最大值時，CC模式下立管在瀉渦前朝來流方向運動。當瀉渦時立管受旋渦影響運動回到中心點，因此其運動與最新的瀉渦頻率接近，產生頻率鎖定。因此在頻率鎖定區域一個典型特征為運動軌跡出現CC模式，可以以此判別頻率鎖定區域，也是能量輸入區域。

為研究在不同流動形式下的能量輸入區域分布規律，對0.2 m/s流速下階梯流的運動軌跡進行深入分析，如圖14所示。并在圖中表明了CC模式為雙向相位差小于180°的運動軌跡。

圖15為階梯流在0.2 m/s時的立管整體振幅隨時間變化的變化圖。對比圖14和圖15的各個工況進行以下分析：在階梯流作用下，z/L為0.4～0.6范圍出現CC模式的運動軌跡，對應地在圖15（a）的橫向振幅圖上，0.3和0.7附近出現最大振幅，而順流向振幅圖同樣在該區域出現了行波效應。

對比分析可以認為在運動軌跡出現CC模式的附近會出現行波效應，而橫向振幅的最大值同樣發生在該區域附近。而行波方向從振幅大的地方向振幅小的區域傳播，即從能量輸入（power-in）區域向能量輸出（power-out）區域傳播。

在階梯流作用下行波效應和駐波效應非常明顯，為了更好地描述駐波和行波之間的關系，分別選取了較高流速0.6 m/s和1.2 m/s的兩種階梯流進行分析。圖16和圖17分別為0.6 m/s和1.2 m/s階梯流雙向振幅隨時間的變化圖譜。駐波區域呈現穩定的振幅，沿立管軸向沒有明顯變化，而行波區域沿著立管軸向存在明顯的位移變化。可以看出：橫向以駐波為主，順流向在邊界和靜止區域出現駐波，行波從階梯流高流速區域向低流速區域傳遞。

4 結 論

本文基于離散點渦法以及柔性梁理論，建立了三維長柔立管渦激振動耦合計算模型，并通過相關試驗數據驗證了模型的有效性。采用提出的模型對階梯流作用下長柔立管渦激振動特性及行波效應進行了分析，得到以下結論：

（1）基于尾流振子模型，通過對雙自由度剛性圓柱渦激振動耦合振子方程進行改進，得到三維長柔立管耦合計算模型，該模型能夠對不同流動形式下的海洋長柔立管響應進行預報。

（2）階梯流作用下，長柔立管在發生渦激振動時，順流向的振動模態為橫向的2倍或更多倍，振動頻率與流速之間存在線性關系，順流向的振動主頻率為橫向振動主頻率的2倍，順流向會出現更高的模態階數，并且存在3倍于橫向主頻率的振動。

（3）階梯流作用下，長柔立管在發生渦激振動時，會在順流向發生明顯的行波效應，行波從CC運動軌跡的區域向C運動軌跡的區域傳遞。在階梯流作用下表現為從流速高的區域向流速低的區域傳遞。