雙蛋型交接耐壓殼設計及屈曲研究

張 建， 左新龍， 王緯波 ， 唐文獻， 李泓運

（1.江蘇科技大學，江蘇 鎮(zhèn)江212003；2.中國船舶科學研究中心，江蘇 無錫214082）

0 引 言

2015年5月，《中國制造2025》把海工裝備作為十大重點發(fā)展領域之一。2016年2月，國家科技部將深海關鍵技術與裝備研發(fā)列為重點專項。“十三五”期間，是我國大洋勘查與深海科學研究的關鍵時期，作為潛水器的重要組成部分，耐壓殼起著保障下潛過程中內(nèi)部設備正常工作和人員健康安全的作用，其重量占潛水器總重的1/4-1/2[1]。耐壓殼的設計對潛水器安全性、機動性、空間利用率和人機環(huán)等性能具有重要影響[2]。

近年來，潛水器下潛深度及水下作業(yè)時間在不斷地刷新紀錄，由于耐壓殼單艙室、模塊集成的缺陷，使得多段交接耐壓殼開始備受關注，但分段殼體輪廓及環(huán)形加強肋嚴重影響整體結構的穩(wěn)定性，一直是多段交接耐壓殼發(fā)展的瓶頸[3]。茍鵬、崔維成[4]對多球交接耐壓殼的結構優(yōu)化問題做了研究，總結了雙球交接耐壓殼的兩種典型破壞模式，提出了三種新的多球交接形式。Garland[5]設計并制作了雙球及三球兩種交接形式的耐壓殼。Hall[6]采用石墨/環(huán)氧樹脂復合材料制造了雙球型耐壓殼的實物模型，并用鈦合金環(huán)肋加強，與相同直徑的鋼質耐壓殼相比，重量減輕了46%。Liang[7]采用EIPF和DFP方法，研究了多球殼大深度潛水器耐壓殼體的優(yōu)化設計問題。Leon[8]試驗研究了雙球型鈦合金耐壓殼的環(huán)形加強肋對其失效載荷的影響規(guī)律。

然而，對于球形耐壓裝備，在實際受載過程中，由于對缺陷非常敏感[9-10]，安全性較差。其次，球形耐壓裝備曲率較小且處處相等，導致內(nèi)部設備布置困難，空間利用率較低，人員舒適性變差，進而降低潛水器的人機環(huán)特性。多球型耐壓裝備在一定程度上擴大了艙室空間，提高了人員舒適性，但仍然無法克服缺陷敏感度高、空間利用率低等缺點[11-13]。因此，能最優(yōu)協(xié)調缺陷敏感度、空間利用率等優(yōu)點的異形殼研究就顯得尤為重要。Magnucki[14]認為交接的桶形耐壓殼可以替代傳統(tǒng)的圓柱形和球形耐壓殼。Jasion[15-17]提出了分別由定常經(jīng)線、卡西歐卵形線及回轉球形曲線等旋轉殼體交接而成的耐壓殼，并進行了詳細的試驗及理論研究。Blachut[18-20]也對由定常經(jīng)線旋轉殼體交接而成的耐壓殼進行了試驗研究，得到了加強肋對殼體失穩(wěn)破壞的規(guī)律。

此外，蛋殼滿足圓頂原理，具有超強的耐壓特性，是一種優(yōu)異的耐壓殼仿生設計原型[21]。張建[22]等研究了千米水深蛋殼仿生耐壓殼的設計理論與分析方法，設計了6 km水深雞蛋殼、鵝蛋殼仿生耐壓殼，并從儲備浮力、殼內(nèi)空間利用率、流線型、乘員舒適性等方面綜合比較，得到鵝蛋殼仿生耐壓殼可為深水耐壓設計提供有效參考；在此基礎上，進一步研究了復合材料蛋形耐壓殼的力學特性，通過理論計算，證明了蛋形耐壓殼綜合性能優(yōu)于球形耐壓殼，可最優(yōu)協(xié)調強度穩(wěn)定性、浮力系數(shù)、空間利用率、人機環(huán)特性以及水動力學特性，且對缺陷敏感性低，便于開孔、開窗，在深海潛水器上具有良好的應用前景[23]。然而，對于單蛋形耐壓殼結構的潛水器，其單艙室空間較小，無法滿足大空間深海潛水器開發(fā)的要求，可在不降低殼體安全性的前提下去除蛋形殼曲率較大的端部，用于開孔連接，會進一步提高空間利用率。

為此，本文開展雙蛋型交接耐壓殼設計及屈曲研究工作。首先，基于前期鵝蛋殼生物學試驗，優(yōu)選蛋形函數(shù)，設計雙蛋型交接耐壓殼結構；接著，建立雙蛋殼無環(huán)肋、有環(huán)肋連接的鈍端/尖端兩種相交形式的258個數(shù)值模型，研究其線性屈曲失穩(wěn)模式，分析環(huán)形加強肋對雙蛋殼線性屈曲行為的影響規(guī)律；最后，提出變形協(xié)調設計理念，研究雙蛋殼的非線性屈曲最終破壞形式，分析鈍端/尖端相交的兩種交接形式對雙蛋殼屈曲行為的影響規(guī)律，并與完整蛋形殼體的靜水壓力試驗和數(shù)值結果對比分析。

1 雙蛋型交接耐壓殼幾何模型

前期研究發(fā)現(xiàn)，單一完整蛋形耐壓殼（以下簡稱：蛋形殼）可在不降低安全性的前提下去除曲率較大的端部，用于開孔連接，會進一步提高空間利用率[23]。采用兩個蛋形殼相連的方案，可進一步增加艙室空間，提高了人機環(huán)特性，同時也便于分段制造[24]。本文設計的雙蛋型交接耐壓殼（以下簡稱：雙蛋殼）由兩個相同的蛋形殼對稱交接而成，參考一般深潛器殼體的結構尺寸，采用無肋骨殼體形式，幾何模型如圖1所示。在前期鵝蛋殼生物學試驗研究中，發(fā)現(xiàn)Kitching蛋形曲線[25]（圖2）與鵝蛋殼經(jīng)線的皮爾遜相關系數(shù)高達99.89%，因此，蛋形殼外輪廓選用Kitching蛋形方程（（1）式），且取B/L=0.69，L/e=45[24]。雙蛋殼交接形式分為尖端相交（圖1）、鈍端相交兩種交接形式。主要幾何參數(shù)包括：雙蛋殼長度Lm、寬度Bm、蛋形殼厚度t、環(huán)形加強肋（以下簡稱：環(huán)肋）長度Lr、雙蛋殼交接開孔直徑Rr（即環(huán)肋外直徑）和環(huán)肋厚度tr（圖1）。

其中：L為蛋殼長軸長度，B為蛋殼短軸長度，e為偏心距。

2 雙蛋殼數(shù)學模型

2.1 蛋形殼受壓變形力學模型

蛋形殼是一種滿足正高斯曲線的多焦點、旋轉薄壁殼體結構[26]。根據(jù)薄殼理論[27]，可確定蛋形殼的幾何方程，如下式所示：

其次，由旋轉殼體理論，可得蛋形殼的本構方程，如下式所示：

此外，根據(jù)蛋形殼幾何方程（（2）式）和本構方程（（3）式），可以得到蛋形殼徑向（第一曲率半徑方向）變形位移w，如下式所示：

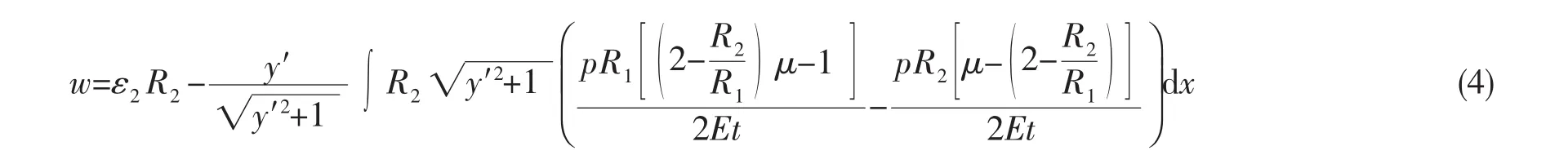
最終，蛋形殼垂直于長軸（旋轉軸）方向的變形位移δ可由下式獲得：

2.2 環(huán)肋主要參數(shù)關系確定

多段交接耐壓殼體主要有兩種破壞形式[4]：一、由于環(huán)肋自身剛度不足，導致殼體變形過大最終屈服破壞；二、環(huán)肋剛度過大，導致交接處的殼體內(nèi)側凹陷破壞，而環(huán)肋和殼體中部仍處于線彈性階段。為了避免出現(xiàn)這兩種破壞現(xiàn)象，且使殼體開孔加強后的變形與完整殼體變形一致，采用蛋形殼與環(huán)肋受力變形一致的設計理念，即變形協(xié)調理念（蛋形殼垂直于長軸（旋轉軸）方向的變形位移δ，與環(huán)肋徑向（垂直于長軸（旋轉軸）方向）位移δr相等）。

雙蛋殼（尖端相交）受力簡圖如圖3所示。根據(jù)線彈性力學理論，環(huán)肋的徑向位移[7]可由下式獲得：

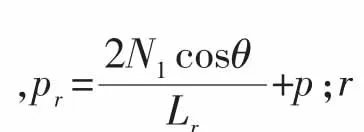
最終，可確定雙蛋殼（尖端相交）環(huán)肋外直徑Rr、環(huán)肋長度Lr和環(huán)肋厚度tr三者之間的關系，如下式所示：

同理，上述也可以得到鈍端相交的雙蛋殼環(huán)肋主要參數(shù)的關系。由此，在雙蛋殼設計中可根據(jù)要求設定兩個參數(shù)，在滿足變協(xié)調理念的條件下，確定第三個參數(shù)。

3 蛋形殼及雙蛋殼數(shù)值模型

運用HYPERMESH軟件，將蛋形殼以古錢幣形式劃分，單元類型選為線性四邊形單元S4，且參考球殼單元平均尺寸與殼體半徑最優(yōu)比0.07[30]，確定蛋形殼網(wǎng)格單元最大尺寸5 mm，以提高分析計算精度，避免網(wǎng)格沙漏，網(wǎng)格模型如圖4所示。此外，耐壓殼體理想情況下不受任何約束，為消除模型的剛性位移，在ABAQUS軟件對模型進行屈曲分析時，選擇模型上不共線的三點，以限制六個方向的位移[30]。殼體模型外部均施加均布載荷p0=1 MPa，材料設定為304不銹鋼，屬性參數(shù)：破壞應力σy=300 MPa，彈性模量E=193 GPa，泊松比μ=0.247。此外，使用微控電子萬能試驗機（MZ-5001D1）對15件304不銹鋼拉伸試件進行彈塑性拉伸試驗，得到數(shù)據(jù)后，擬合現(xiàn)有不銹鋼彈塑性公式[31]，獲得304不銹鋼應力—應變公式，如（8）式所示，可提高模擬仿真準確度。

4 結果分析與討論

4.1 線性屈曲分析

薄殼耐壓結構穩(wěn)定性分析相對強度校核而言，占設計的主要因素[28]。當殼體失穩(wěn)時，整體結構會發(fā)生較大變形，穩(wěn)定性分析顯得尤為重要。對于多段交接耐壓殼體，環(huán)肋對其穩(wěn)定性分析影響較大。為此，設計無環(huán)肋、有環(huán)肋加強的兩種連接方式。一是無環(huán)肋連接：建立雙蛋殼鈍端相交（圖4（c））、尖端相交（圖4（b））模型，主要幾何參數(shù)：蛋形殼寬度Bm=160 mm，蛋形殼長度L=232 mm，蛋形殼厚度t=1 mm，蛋形殼偏心距e=5 mm，雙蛋殼交接開孔直徑Rr=60 mm，環(huán)肋長度Lr=0 mm；二是有環(huán)肋連接：以蛋形殼尖端對稱，與環(huán)肋依次連接的耐壓結構（圖4（d）），且不同環(huán)肋長度Lr（表1）和環(huán)肋厚度tr（表2）組合的共128個雙蛋殼（尖端相交）模型，其蛋形殼主要幾何參數(shù)與無環(huán)肋連接的蛋形殼相同。同樣，建立蛋形殼鈍端相交（圖4（e））的128個雙蛋殼（鈍端相交）模型。利用ABAQUS軟件對這258個雙蛋殼模型（無環(huán)肋、有環(huán)肋）線性屈曲求解，分別獲得這兩種交接（鈍端相交、尖端相交）形式下，且不同環(huán)肋參數(shù)模型的臨界屈曲模態(tài)及載荷，如圖5-6所示。此外，建立蛋形殼模型（圖4（a）），作對比分析研究，計算結果如圖5（a）所示。

表1 環(huán)肋長度Lr取值Tabl.1 Length value(Lr)of rib ring

表2 環(huán)肋厚度tr取值Tab.2 Thickness value(tr)of rib ring

圖5是蛋形殼及雙蛋殼（無環(huán)肋）屈曲模態(tài)。可見，蛋形殼失穩(wěn)發(fā)生在中部，雙蛋殼（無環(huán)肋）失穩(wěn)發(fā)生在交接處。相比較蛋形殼臨界屈曲載荷（12.121 MPa），雙蛋殼的臨界屈曲載荷（鈍端相交6.431 MPa，尖端相交7.012 Mpa）降低了近45%。在增大殼體內(nèi)部空間的同時，雙蛋殼（無環(huán)肋）極大地降低了結構穩(wěn)定性，是不可取的。為此，需要對雙蛋殼交接處進行環(huán)肋加強，以尋求結構穩(wěn)定性的提升。

圖6是雙蛋殼（有環(huán)肋）在兩種交接（鈍端相交（圖4（d））、尖端相交（圖4（e））形式下，且不同環(huán)肋參數(shù)模型的臨界屈曲載荷。兩種交接形式的雙蛋殼在環(huán)肋長度Lr一定時，臨界屈曲載荷均隨環(huán)肋厚度tr增加而增大，而這種增大趨勢隨環(huán)肋長度Lr增大而減緩。此外，當環(huán)肋厚度tr增加到約1.5 mm以后時，雙蛋殼的臨界屈曲載荷達到一個平臺，即改變環(huán)肋長度Lr和環(huán)肋厚度tr，臨界屈曲載荷值（鈍端相交12.059 MPa，尖端相交12.078 MPa）保持不變。可見，經(jīng)過環(huán)肋加強后的雙蛋殼，其臨界屈曲載荷已基本趨于蛋形殼。

圖7為環(huán)肋長度Lr=15 mm時，兩種交接形式的雙蛋殼臨界屈曲載荷隨環(huán)肋厚度 tr的變化曲線（即圖6（a）、6（b）中 A、B曲線）。顯然，這兩種交接形式的雙蛋殼變化趨勢基本一致，均在p點（tr=1.5 mm）后，臨界屈曲載荷達到最大值，且保持不變。此外，由圖7可知，p點之前，雙蛋殼失穩(wěn)（S-1，B-1）發(fā)生在交接處；p 點之后，即臨界屈曲載荷達到最大值時，雙蛋殼失穩(wěn)（S-2，B-2）均發(fā)生在交接的蛋形殼中部，形式與蛋形殼一致。可見，經(jīng)過環(huán)肋加強后的雙蛋殼，其屈曲模態(tài)與蛋形殼一致，模態(tài)縱波數(shù)也均為10。

其次，選定環(huán)肋長度Lr=15 mm，根據(jù)變形協(xié)調理念（本文第二章），由（7）式可以分別獲得尖端相交雙蛋殼的環(huán)肋厚度2.9 mm，鈍端相交雙蛋殼的環(huán)肋厚度3.4 mm。如圖7所示，理論獲得的環(huán)肋厚度對應曲線上的a、b點。可知，根據(jù)變形協(xié)調的設計理念計算的結果較為保守穩(wěn)妥。

4.2 非線性屈曲分析

線性屈曲分析主要針對理想殼體結構的線彈性屈曲行為，分析結果往往過于保守。缺陷是影響結構失穩(wěn)的主要原因，其中幾何缺陷是臨界屈曲載荷下降的最主要因素[32]，引入初始缺陷可以更為準確地預測殼體破壞形式。非線性屈曲分析可引入線性屈曲模態(tài)作為幾何初始缺陷。選取上述通過理論確定的環(huán)肋尺寸（本文第4.1節(jié)），建立兩種雙蛋殼模型，主要尺寸參數(shù)如下：鈍端相交形式，環(huán)肋長度Lr=15 mm，環(huán)肋厚度tr=3.4 mm；尖端相交形式，環(huán)肋長度Lr=15 mm，環(huán)肋厚度tr=2.9 mm。此外，根據(jù)歐洲標準規(guī)范（ENV1993-1-6），設定缺陷因子0.5 mm。利用ABAQUS軟件計算蛋形殼及雙蛋殼非線性屈曲行為，材料屬性可由（8）式獲取，選取第一階屈曲模態(tài)作為初始缺陷，分析結果如圖8所示。其中，橫坐標為短軸方向最大位移Δ與蛋形殼厚度t之比；縱坐標為可承載載荷pep與外部施加載荷p0之比。

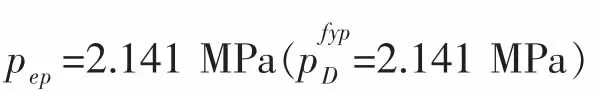
蛋形殼在平衡路徑峰值點C處的模態(tài)見圖8C，與線性屈曲模態(tài)（圖5（a））一致，均在蛋形殼中部發(fā)生失穩(wěn)。峰值點C后的后屈曲模態(tài)，蛋形殼中部出現(xiàn)凹坑最終失效形式（圖8c），與304不銹鋼等比例實物蛋形殼（Bm=160 mm，L=232 mm，t=1 mm，e=5 mm）的靜水壓力試驗結果一致（圖9（b））。

雙蛋殼（鈍端相交）在平衡路徑峰值點A處的模態(tài)見圖8A，與蛋形殼屈曲模態(tài)（圖8C）一致，均在兩個蛋形殼中部發(fā)生失穩(wěn)。峰值點A后的后屈曲模態(tài)，雙蛋殼在相交的一個蛋形殼中部出現(xiàn)凹坑，并最終失效（圖8（a）），與蛋形殼最終失穩(wěn)模式（圖8（c））一致。此外，尖端相交的雙蛋殼非線性屈曲模態(tài)與鈍端相交的雙蛋殼相同，見圖8。綜上，應用變形協(xié)調理念對雙蛋殼進行環(huán)肋加強后，雙蛋殼的非線性屈曲載荷/模態(tài)不會受影響，并與蛋形殼基本一致。形殼開孔連接后結構的失穩(wěn)及缺陷敏感特性。此外，當雙蛋殼承受載荷

5 結 論

（1）環(huán)肋對雙蛋殼結構穩(wěn)定性影響較大，當環(huán)肋厚度增加到一定值后，其臨界屈曲載荷到達峰值平臺，并趨于蛋形殼的臨界屈曲載荷。變形協(xié)調理念設計的環(huán)肋厚度略大于滿足臨界屈曲載荷的環(huán)肋厚度的臨界值（拐點p點，見圖6），該設計方法較為保守穩(wěn)妥。

（2）采用變形協(xié)調理念設計環(huán)肋加強后的雙蛋殼，其線性屈曲模態(tài)與蛋形殼一致，均在殼體中部發(fā)生失穩(wěn)（縱向波數(shù)均為10），且臨界屈曲載荷基本趨于蛋形殼。引入初始幾何缺陷，對變形協(xié)調理念設計的雙蛋殼進行非線性屈曲分析，發(fā)現(xiàn)失效形式與蛋形殼無差異，均在材料塑性變形階段殼體中部出現(xiàn)凹坑，并逐漸增大最終破壞，同時也與蛋形殼實物模型試驗結果一致。

（3）雙蛋殼繼承了蛋形殼的中度缺陷敏感性，表明加強后的雙蛋殼不會改變完整蛋形殼原有的耐壓機制，不會降低整體結構的穩(wěn)定性，也不會增加缺陷敏感度。此外，雙蛋殼的兩種交接形式（鈍端相交、尖端相交）的失效破壞模式基本一致。鈍端相交的雙蛋殼臨界屈曲載荷要略大于尖端相交形式的。