任意邊界條件下變厚度中厚矩形板的靜動態特性分析

吳子奇，王 治，史冬巖，王青山，姚熊亮

（1.哈爾濱工程大學 a.船舶工程學院；b.機電工程學院，哈爾濱150001；2.中南大學 機電工程學院，長沙410083）

矩形板結構作為主要的結構構件，已經被廣泛應用于航空航天、機械、建筑、造船、橋梁等領域，在實際工程中，除了等厚度矩形板以外，變厚度板也有著廣泛的應用價值，特別是在一些特殊的土建水利等方面。因此研究變厚度板的靜動態特性具有較為重要的工程價值，使設計者在進行變厚度結構設計時能夠了解其靜動態特性。

從現有研究文獻來看，在以往的研究中，對于等厚度結構的研究成果較為豐碩，其中主要的研究方法包括辛本征值展開法、無網格數值解法、離散積分法等，但是上述方法中的推導過程與求解過程都較為繁瑣，邊界條件較為單一，對于一般邊界條件下的靜動態特性無法計算；對于變厚度中厚板靜動態特性的研究，從現有文獻來看其主要的研究方法包括雙重傅立葉級數[9]、半解析解法[10-13]、二次樣條函數[14]、廣義微分求積法[15]、辛幾何法[16]和能量法[17]，對這些方法進行總結不難發現，大部分的方法都只局限于簡單的經典邊界條件，對于一般邊界條件并不能進行求解，且求解過程較為繁瑣。文獻[18]提出了一種改進傅立葉級數方法，建立了一般邊界條件下矩形薄板的靜動態法分析模型，與傳統的傅里葉級數相比收斂性有較大改善，且精度較高。

本文基于現有文獻研究的不足，利用改進傅立葉級數研究方法，建立了一般邊界條件下等厚度與變厚度矩形板結構的靜動態特性分析模型。首先將結構的橫向位移與旋轉角度函數用改進傅立葉級數進行展開，并且對其進行能量描述。其次將函數展開的未知傅立葉級數系數作為廣義向量，利用Rayleigh-Ritz方法進行求解，得到一個標準特征值問題。通過這個特征方程組，就能簡便得到結構的靜動態特性。本文建立的模型能夠對于等厚度與變厚度中厚板結構在一般邊界條件下的靜動態特性進行求解。最后通過大量的數值算例對本文方法進行了驗證，證明了本文方法的合理性，而且具有良好的計算精度和收斂速度。

1 矩形厚板彎曲振動理論模型

1.1 結構物理模型

本文所研究的變厚度Mindlin矩形板模型如圖1所示，在直角坐標系（x，y，z）中，長為a，寬為b，厚度為h（x）的變厚度中厚矩形板。對于板結構中的任一質點，其橫向振動位移函數采用w來描述，其單位為m；轉角位移函數采用ψx和ψy來表示，其單位為m。板的一般邊界條件可以采用沿各邊均勻分布的線性位移（kil，i取值為 x、y，l的取值為0、a、b，在后面不再進行描述）和旋轉約束彈簧（Kil）來模擬。由于結構在邊界處還存在扭矩，因此為了更加精確地對其進行求解，在邊界處還引入扭轉彈簧類型（Kijl）來對其扭矩效果進行模擬，各種經典的邊界條件可以通過改變彈簧剛度值的大小而簡單實現。當沿邊界分布的兩類約束彈簧剛度值均為無窮大時，則為固支（C）邊界條件。通過將兩類約束彈簧剛度值設定為0時，則簡單地實現自由（F）邊界條件。簡支（S）邊界條件則可以通過將邊界上線位移和旋轉約束彈簧剛度值分別設置為無窮大和極小數而簡便實現。對于邊界上的線位移和旋轉約束彈簧剛度的單位分別為N/m2和Nm/rad。板結構的邊界條件采用逆指針順序來進行描述，順序如下：y=0、x=a、y=b、x=0。在本文計算中，無窮大的剛度值取為1×1014，而極小剛度值取為零。

1.2 結構運動關系與本構關系

根據線性小彈性變形理論，結構應變分量與結構位移變量之間的關系可以定義為：

根據胡克定律，應力與應變之間的關系定義為：

其中：

E為結構彈性楊氏模量，單位為Pa，μ為材料的泊松比，κ為剪切修正因子。

在物理模型的描述中可知，對于結構的一般邊界條件模擬是依據設置在邊界處的三類彈簧剛度來進行模擬，因此一般彈性邊界可以表示為

其中：kx0（kxa）、ky0（kyb）分別代表 x=0（a）和 y=0（b）邊上橫向線性位移彈簧剛度系數，單位 N/m2；Kx0（Kxa）、Ky0（Kyb）分別代表 x=0（a）和 y=0（b）邊上旋轉約束彈簧剛度系數，單位 N/rad；Kxy0（Kxya）、Kyx0（Kyxb）分別代表 x=0（a）和 y=0（b）扭轉約束彈簧剛度系數，單位 Nm/rad。

1.3 位移容許函數

在本文方法中，構造合適的位移容許函數對本文的研究有著很重要的關系。在以往的求解方法中，結構容許函數往往是根據相同邊界下的梁函數進行設置，因此，不同的邊界條件，需要自定義不同邊界下的梁函數。這就會導致，當邊界條件發生改變時需要設置不同類型的梁函數，當函數發生改變，整個求解過程需要重新推導與編程計算，不具有通用性，工作量繁瑣。結構的容許函數除了設置成梁函數以外，還可以用簡單、正交多項式和三角函數進行表示。當容許函數為多項式時，將容許函數展開為低階多項式時，不能滿足結構在高階次的振動求解；展開為高階多項式時，由于數值計算截斷誤差的原因會引起數值不穩定。當容許函數為傳統傅立葉三角級數時，級數取無窮項時能夠構成一個完整的無限維度向量空間，通過數值截斷進行計算時，該容許函數具有良好的數值穩定性和一定的計算精度，也許可以克服多項式或者梁函數存在的問題。然而，傳統的傅立葉級數在邊界處會存在收斂性問題，除了簡單的經典邊界以外。因為，當容許函數展開為傳統傅立葉三角級數時，其位移導數在邊界處可能存在不連續現象，因此，可能導致不連續或者收斂速度極慢，不能滿足結構的振動控制微分方程。為了克服這些難點，一種改進的傅立葉級數表達已經被提出，并且被應用到一般彈性邊界下正交各向異性矩形薄板[18]的彎曲自由振動和環扇形板[19]的面內振動分析。在本文中，進一步將該方法擴展到變厚度中厚板結構的靜動態特性分析中。因此，為了滿足任意邊界條件下的厚板結構，結構的位移函數與旋轉函數被包含正弦三角級數的改進傅立葉級數。

在Mindlin板理論，位移分量假設由下式給出：

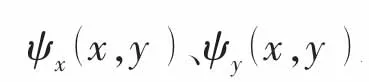
對于一般邊界條件下中厚矩形板結構來說，其橫向振動和轉角位移函數可以采用二維改進傅里葉級數方法來進行表示：

1.4 能量泛函與求解步驟

在采用改進傅里葉級數建立了中厚矩形板的位移函數之后，需要對位移函數的未知傅里葉展開系數進行求解。由于本文所建立的位移函數足夠光滑，位移函數的弱解（近似解）和強解（精確解）在數學意義上是等效的。因此，本文采用基于能量原理的Rayleigh-Ritz法來求解未知傅里葉展開系數。變厚度板的應變勢能為：

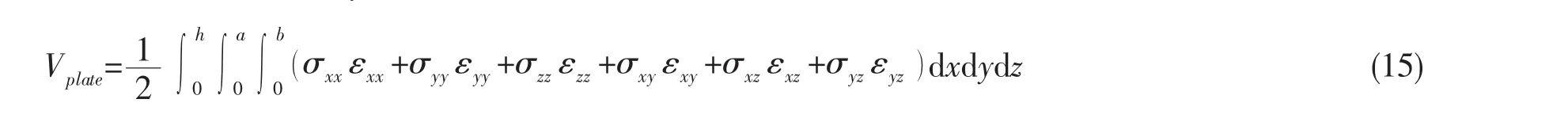
將（1）、（2）式代入（15）式，結構的應變能可以表示為：

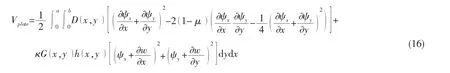
儲存在邊界的彈簧勢能可以表示為：

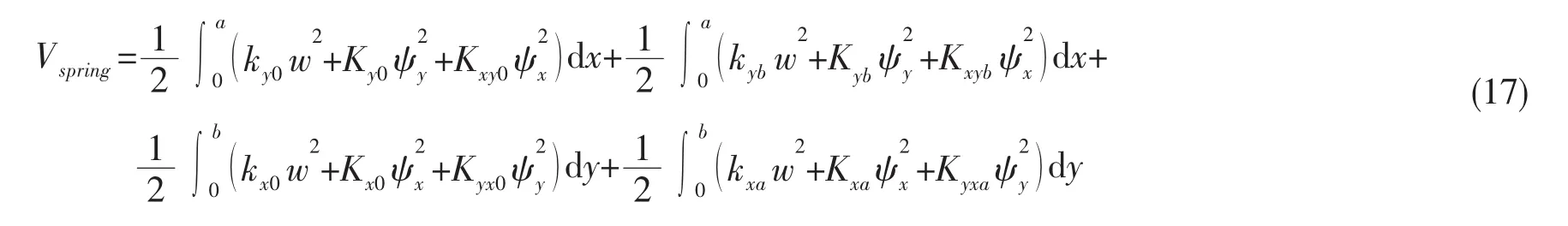
當為一般彈性邊界條件時，將彈簧考慮為無質量質點，此時結構的整體動能為

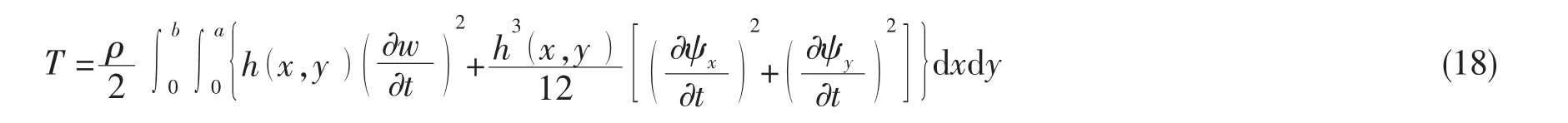
在理論模型的推導中，板的厚度h（ x，y）一般地表示為一個空間坐標函數。為了描述的統一和計算的方便，將空間坐標函數都采用一維或二維傅里葉級數來表示。由于板厚度的空間坐標函數為h（ x，y），板結構的厚度函數可以表示為二維傅里葉余弦級數

其中，傅里葉展開系數可以從下式進行計算：

為了簡便起見，本文以沿x方向線性變化的中厚矩形板作為研究對象，假定厚度變化函數為

從而，板結構的厚度函數通過（19）式可以表示為一維的傅里葉余弦級數

其中，傅里葉展開系數根據（20）式可以計算得到

對施加在Mindlin矩形板上的外載荷所作功Wext可以表示為如下形式：

本文中將在兩種不同類型的載荷下對Mindlin矩形板進行靜態特性分析，這兩種載荷形式分別為均布壓強和線性壓強。

其中：x1≤x≤x2，y1≤y≤y2為壓強載荷作用有效區域。

為了得到結構位移函數的未知展開傅立葉系數，本文采用Rayleigh-Ritz方法進行求解。因為Rayleigh-Ritz方法作為一種數值近似解法，具有求解原理明晰、操作簡單、計算效率高等優點。通過結構的應變勢能、彈簧勢能、動能以及外力功，結構的拉格朗日能量泛函可以表示為

將（10）-（12）式代入（26）式，對未知的傅立葉展開系數求極小值

結構的振動問題將轉換為一個求特征值與特征向量的簡單數學問題，將其矩陣化可以表示為

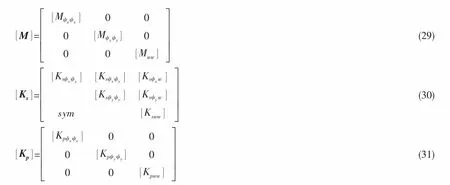
進行靜態分析時，令（28）式中ω=0，則矩形板結構的橫向彎曲振動位移的傅里葉系數向量可表示為：

得到位移的傅立葉系數后，代入（12）式即可得到矩形板的橫向振動位移，通過對矩形板位移進行一系列數學操作即可得到其它感興趣的物理量，諸如對位移求導能得到此時矩形板的速度和加速度等。

2 數值結果與分析

在本節中，將采用上一小節的理論模型，對不同邊界下變厚度中厚板的靜動態特性進行求解，將本文方法得到的計算結果與文獻解及有限元計算結果進行對比驗證，以驗證本文方法的合理性。由于本文方法在計算過程中對級數進行階段計算，所以首先對本文方法的收斂性進行分析；其次，對等厚度與變厚度下的靜動態特性進行了研究分析。

2.1 本文方法收斂性研究

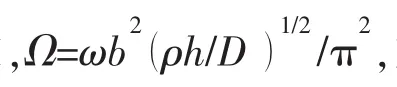
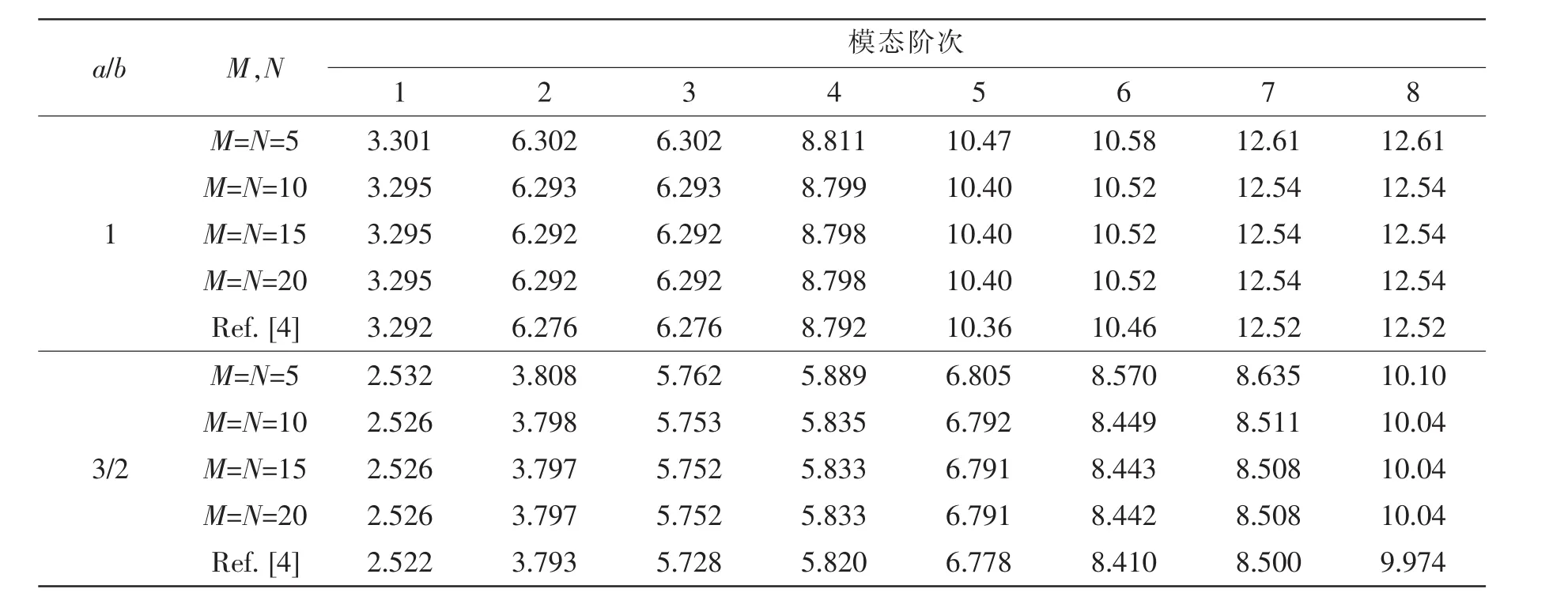
表1 不同截斷數下CCCC勻厚中厚矩形板前8階頻率參數ΩTab.1 Frequency parameters Ω for CCCC moderately thick plates with uniform thickness and different truncate numbers

2.2 等厚度Mindlin矩形板靜動態特性分析

本小節將對經典邊界條件與彈性邊界下的等厚度Mindlin矩形板進行靜動態特性分析，靜態特性主要分析Mindlin矩形板受局部壓強下的位移變形，動態特性包括經典邊界與一般彈性邊界下的模態分析。在本小節所有算例計算中，矩形板的材料參數E=2×1011Pa，泊松比μ=0.3，密度為7800 kg/m3，矩形板結構參數設定為a=4 m，b=2 m；h/b=0.1，0.15，0.2。此外，由于缺少相關文獻數據，為檢驗本方法的正確性，本小節的結果同有限元軟件ABAQUS計算所得數據進行了比較，采用ABAQUS求解時矩形板所使用的單元類型為S4R單元，物理結構參數與邊界條件與本文方法保持一致，網格尺寸為0.01 m×0.01 m。 其中表2-3 中（x1，x2，y1，y2）表示外界載荷作用在矩形板的范圍，例如（2，3，1，2）表示外界載荷作用于矩形板的范圍為x=2，x=3以及y=1，y=2所圍成的矩形區域。

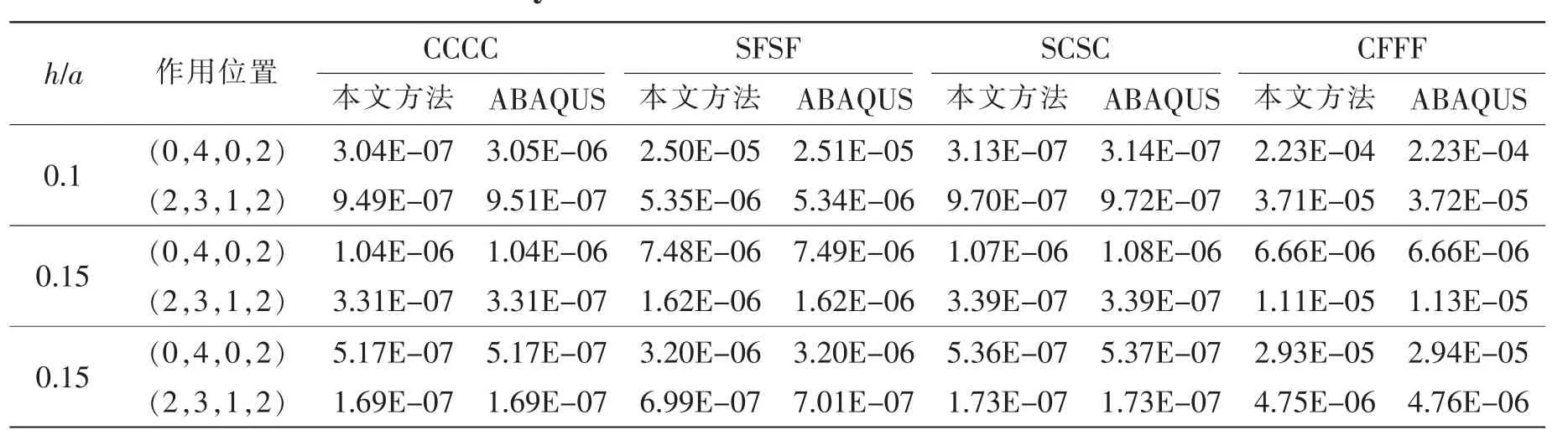
表2 均布壓強P=1000 Pa作用于Mindlin矩形板下的最大變形 單位：mTab.2 The max structural deformation for moderately thick plates with uniform thickness and different boundary condition under load P=1000 Pa

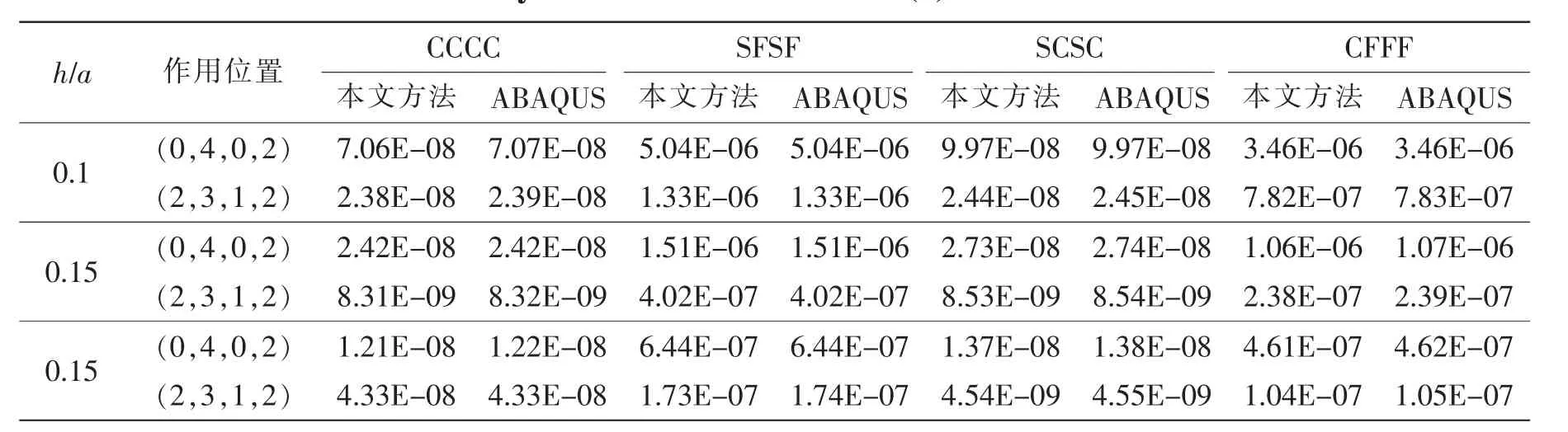
表3 Mindlin矩形板在線性壓強P（x）=100x+1 Pa作用下的最大變形 單位：mTab.3 The max structural deformation for moderately thick plates with uniform thickness and different boundary condition under load P(x)=100x+1 Pa

表2列出了均布壓強在各種經典邊界條件任意組合下在不同跨度比h/b、不同作用區域下結構的最大變形。表3列出了線性壓強在各種經典邊界條件任意組合下在不同跨度比h/b、不同作用區域下結構的最大變形。通過表2～3比較發現本文方法同有限元軟件ABAQUS所得計算結果吻合良好，說明了本方法的正確性。同時也可以看出邊界條件的變化對矩形板的變形影響很大，此外相同的邊界條件和載荷形式及其大小，由于載荷作用的位置變化也會引起板結構最大變形的不同。圖2與圖3給出了 Mindlin 矩形板在 FCSC 邊界條件下，均布壓強載荷作用范圍分別為（0，4，0，3）和（2，3，1，2）時Mindlin矩形板的最大變形圖。由兩組圖形對比可知，兩組圖形中的矩形板受外界載荷后變形一致，進一步說明了本文方法的正確性。

接下來對等厚度中厚板的動態特性進行研究，由（28）式可知，模態特性可以通過求解一個標準的線性方程組簡單得到。表4給出了不同經典邊界條件及長寬比下結構前8階固有頻率參數，文獻解及有限元分析結果作為參照值也在表4中列出，通過表4可知，本文方法的計算結果與文獻解及有限元分析結果吻合良好。表5給出了彈性邊界條件方板結構前6階頻率參數，邊界處的彈性參數為kx0=kxa=ky0=kyb=Γw與Kx0=Kxa=Ky0=Kyb=Γx，扭轉彈簧剛度系數與旋轉彈簧保持一致，有限元分析結果作為參考值也列在表6中。通過表6可知，本文的計算結果與有限元計算結果吻合良好，因此本文方法對于任意邊界條件下的等厚度Mindlin求解是可行的。

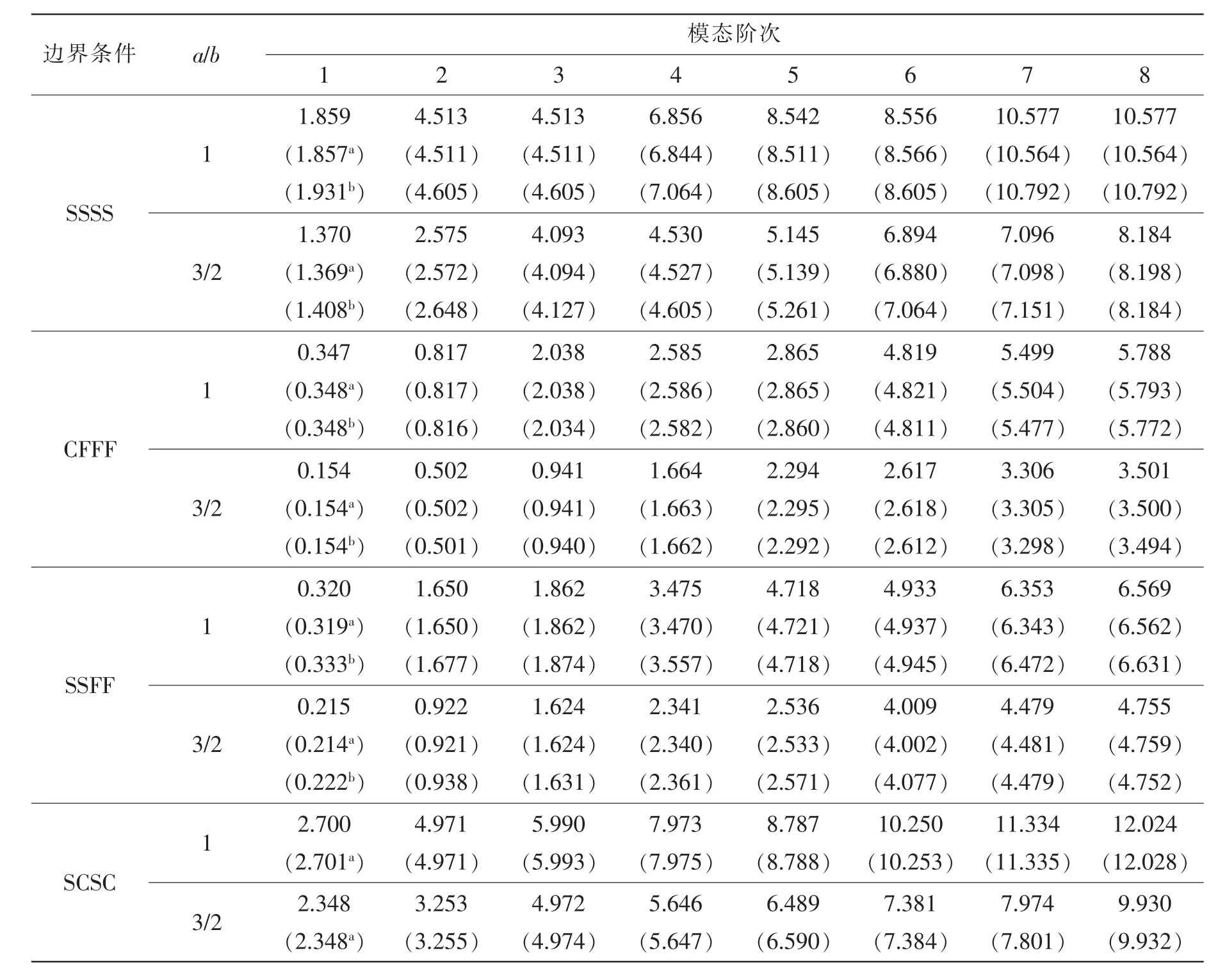
表4 不同邊界條件下勻厚中厚矩形板前8階頻率參數ΩTab.4 Frequency parameters Ω for moderately thick plates with uniform thickness and different boundary conditions

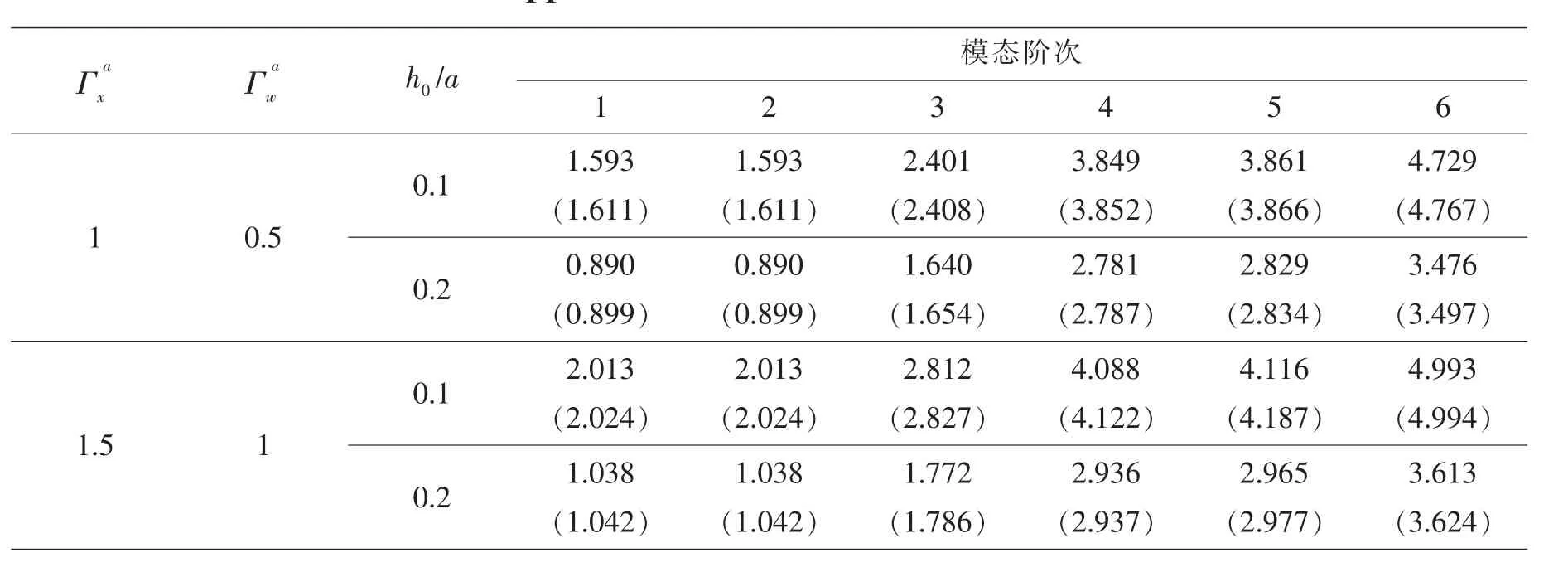
表5 彈性邊界條件下方板結構前6階無量剛化固有頻率參數ΩTab.5 Frequency parameters Ω for moderately square thick plates with uniform thickness and elastic rotation support

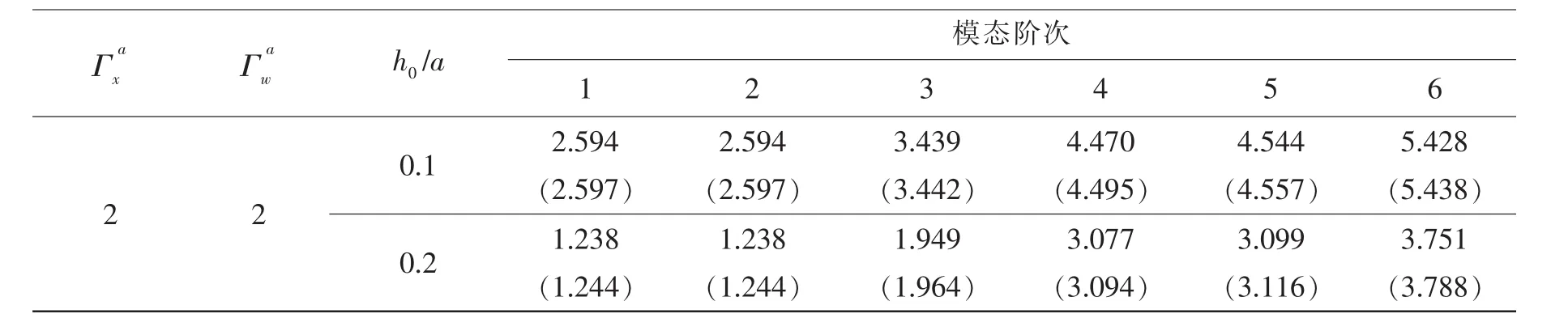
續表5

2.3 變厚度Mindlin矩形板靜動態特性分析

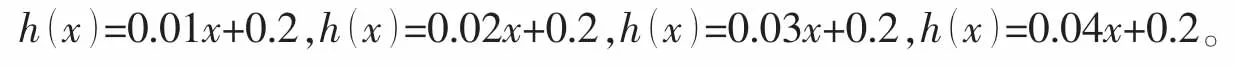
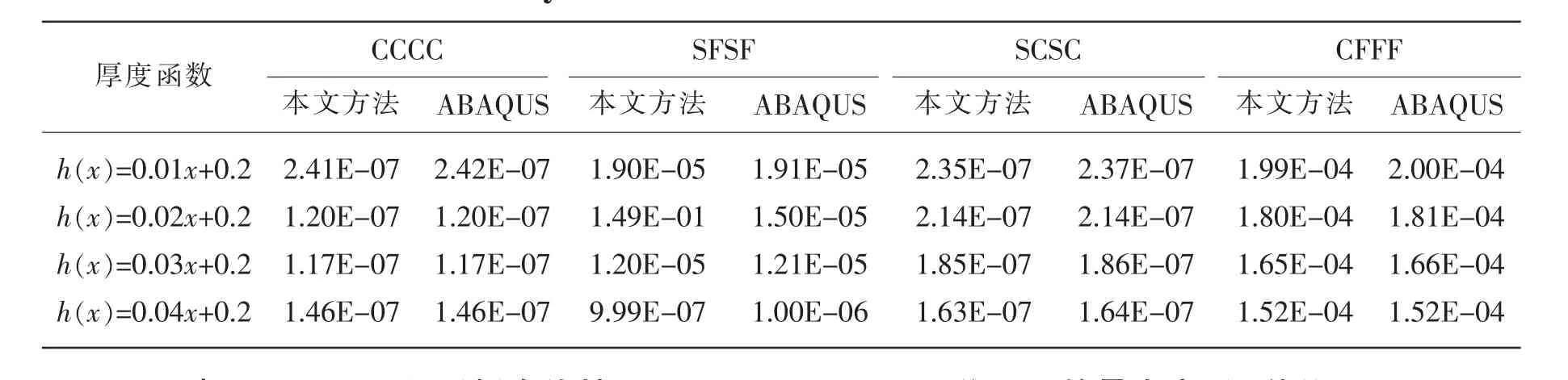
表6 均布壓強P=1000 Pa作用于Mindlin矩形板下的最大變形單位：mTab.6 The max structural deformation for moderately thick plates with variable thickness and different boundary condition under load P=1000 Pa unit：m

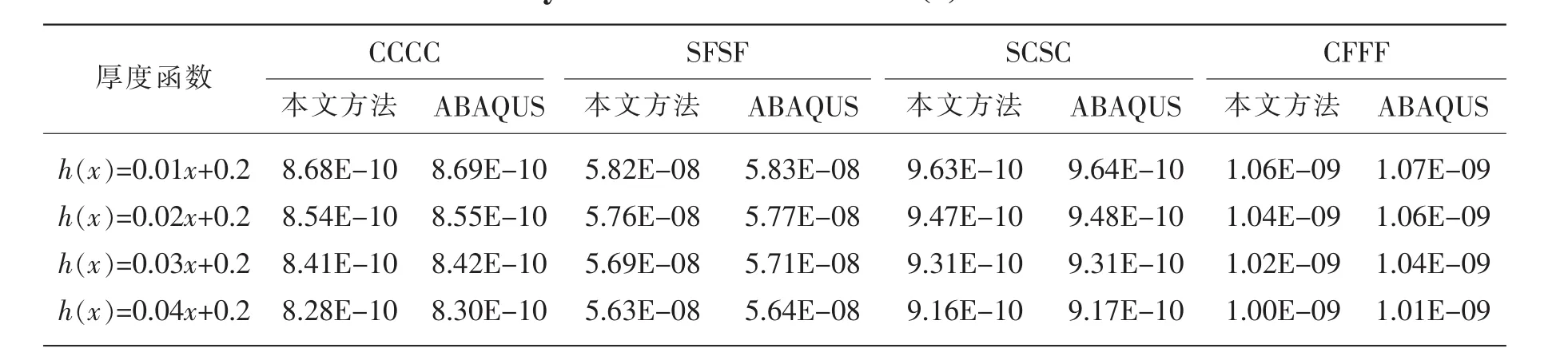
表7 Mindlin矩形板在線性壓強P（x）=100x+1 Pa作用下的最大變形 單位：mTab.7 The max structural deformation for moderately thick plates with variable thickness and different boundary condition under load P(x)=100x+1 Pa unit：m

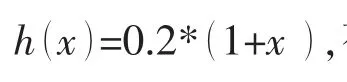
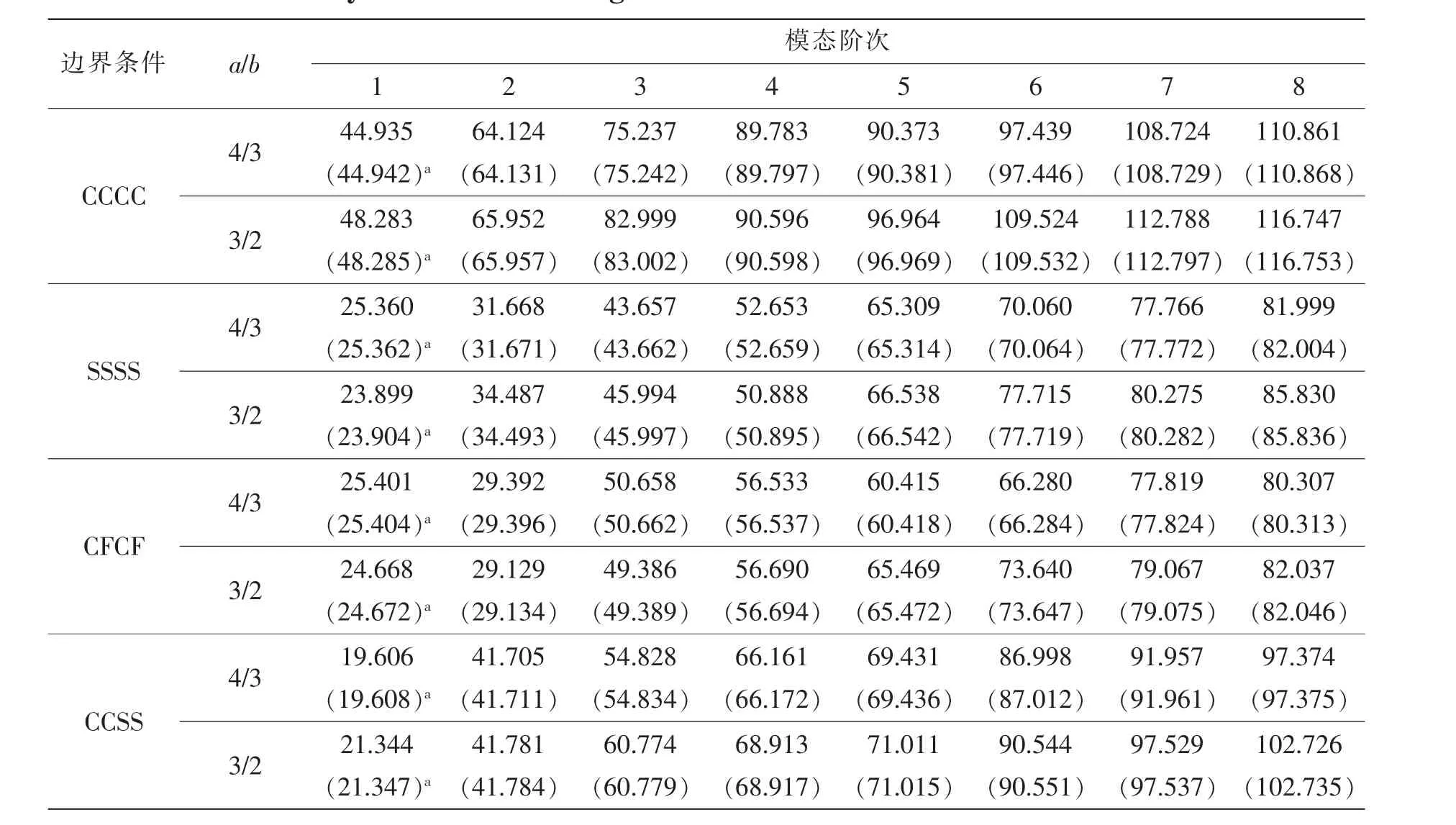
表8 不同邊界條件下變厚度中厚矩形板前8階頻率參數ΩTab.8 Frequency parameters Ω for variable thickness square plates with different boundary condition and length-with ratio

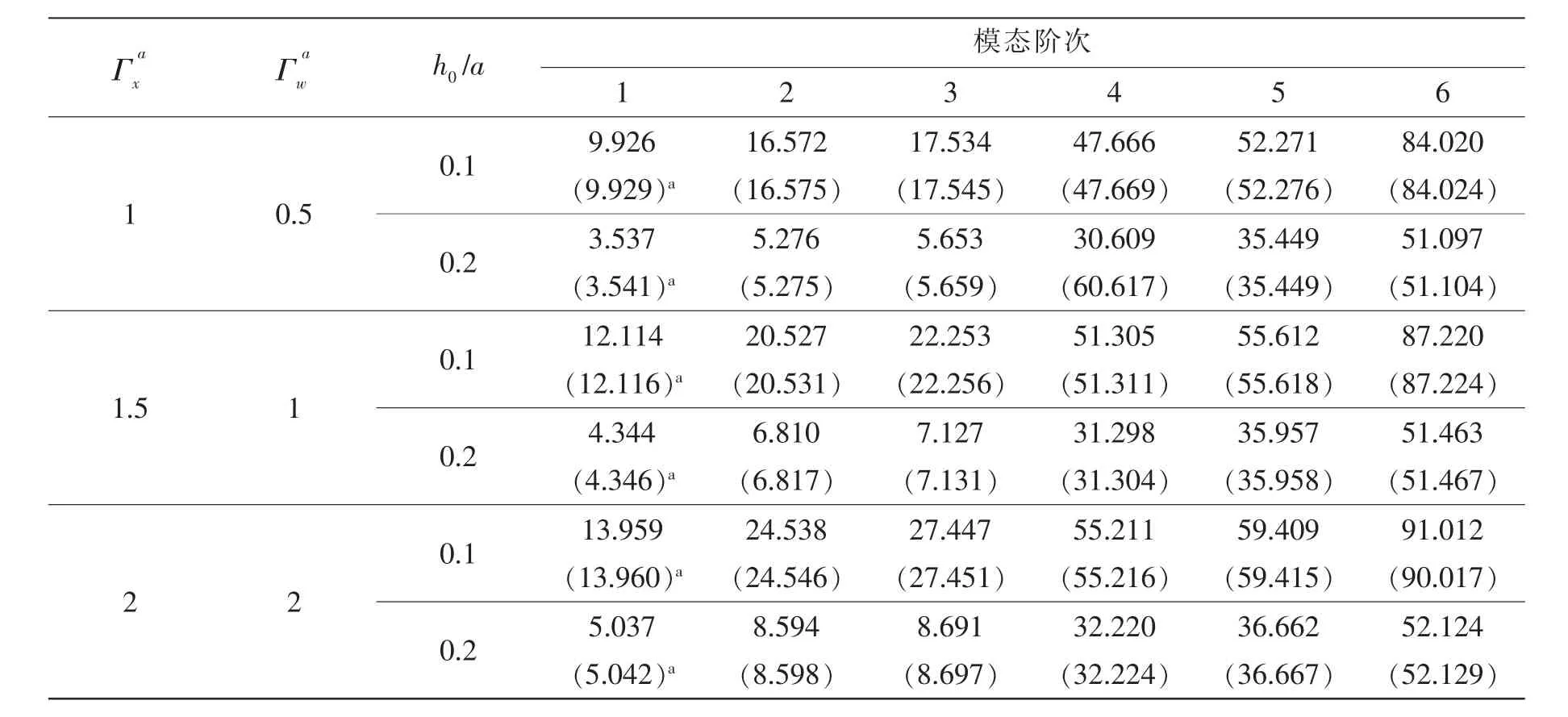
表9 彈性邊界條件下方板結構前6階無量剛化固有頻率參數ΩTab.9 Frequency parameters Ω for moderately square thick plates with variable thickness and elastic rotation support

3 結 論

本文基于傅立葉級數方法建立了任意邊界條件下變厚度Mindlin板的靜動態特性分析模型。該方法主要是將結構的位移容許函數利用改進傅立葉級數形式進行展開。在結構的邊界處采用三類彈簧均勻布置來模擬任意邊界支撐條件。將未知系數作為廣義變量，結合Rayleigh-Ritz法對未知傅立葉展開系數求極值，將矩形厚板的彎曲振動問題轉換為一個簡單求解標準特征值問題。通過大量的數值算例，驗證了本文方法的正確性和可靠性，并得出以下結論：

（1）任意邊界條件下的變厚度Mindlin板位移容許函數可表示為一種通用的改進傅立葉三角級數形式；

（2）對級數進行截斷后，隨著截斷項數的增加，計算結果快速收斂，并且數值穩定性很好；

（3）對于不同邊界下的變厚度Mindlin板的靜動態特性可以實現快速分析，無需重新推導與編程；

（4）除了單向線性變厚度，本文方法還可以很容易求解雙向非線性厚度變化的結構的靜動態特性，具有良好的擴展性。