柔索牽引式機器人的姿態自適應調節控制優化*
陸興華, 葉銘銘, 陳俊祥, 吳宏裕
(廣東工業大學 華立學院,廣東 廣州 511325)
0 引 言
采用智能機器人進行柔索牽引作業,能有效提高柔索牽引作業的智能性,改善牽引和搬運作業的效率。在柔索牽引機器人的設計中,進行機器人的末端位姿的跟蹤測量和參數調節是關鍵,根據柔索牽引機器人幾何參數得到機器人末端位姿,獲得的連桿模型參數能及時反饋給柔索牽引機器人,實現參數修正,提高機器人的控制穩定性和輸出行為指向性。因此,研究柔索牽引機器人的末端位姿控制方法具有重要意義[1]。
目前柔索牽引機器人運動學末端位姿控制的方法主要有圓周點法、模糊比例—積分—微分(proportional-integral-differiential,PID)控制方法、運動學回路法和反演積分控制方法等[2,3]。前三種是將柔索牽引機器人的關節軸線抽象成一條空間中的直線,利用關節軸線間的幾何關系求出機器人的幾何運動參數,采用空間動力學模型進行機器人的穩態位姿調節,完成柔索牽引機器人的控制。后者采樣反演控制律進行柔索牽引機器人的位姿測量和模糊控制,結合自適應控制律進行機器人的位姿參數調節和優化控制,提高跟蹤性能,文獻[4]提出一種基于動態跟蹤測量的柔索牽引機器人末端位姿優化控制方法,根據柔索牽引機器人幾何參數得到柔索牽引機器人末端位姿,采用改進擴展卡爾曼濾波方法進行位姿參量融合,提高控制穩定性,但該方法的抗干擾能力不強;文獻[5]提出一種基于反演穩態誤差補償的柔索牽引式機器人擾動控制方法,實現大范圍的高精度定位和姿態調節,采用時滯跟蹤補償模型構建柔索牽引式機器人控制的約束參量模型,提高機器人控制的人工智能性,但該方法在受到強擾動下的控制穩定性不好[6]。
針對上述問題,本文提出一種基于多傳感器參量融合的機器人姿態自適應調節方法。設計柔索牽引式機器人的7自由度運動學模型,通過仿真實驗進行性能測試,表明了本文方法在提高機器人的姿態控制穩定性方面的優越性能。
1 機器人的運動學模型與力學參量分析
1.1 柔索牽引式機器人的運動學模型
為了實現對柔索牽引作業智能機器人的穩定控制,構建柔索牽引作業智能機器人的慣性姿態融合空間運動學模型,需要進行柔索牽引作業智能機器人的7自由度運動空間規劃,設計柔索牽引式機器人的7個旋轉自由度運動模型,采用末端位姿估計器進行柔索牽引式機器人的姿態特征傳感采集和控制約束參量分析[7],設計柔索牽引式機器人的7自由度運動學模型,如圖1所示。
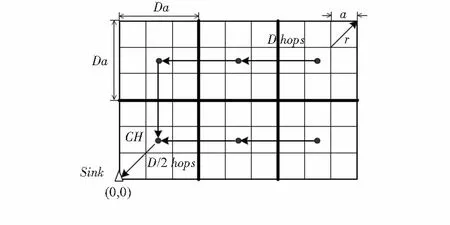
圖1 柔索牽引式機器人的運動空間規劃模型
以圖1所示機器人的運動空間規劃模型為研究對象,采用多傳感器融合跟蹤識別方法進行柔索牽引作業和位姿參量調節[8],傳感器分別為加速度傳感器、磁力傳感器和轉向傳感器等,在多媒體視覺模型下進行柔索牽引作業動態模擬和智能控制,在柔索牽引式機器人6個自由度中采集機器人的定姿參數,得到柔索牽引式機器人的運動學分布的正則方程為
xL3=l1sinθ1+l2sin(θ1-θ2)+α3sin(θ1-θ2+θ3)-α0
(1)
xR3=α6-l5sinθ6+l4sin(θ5-θ6)-
α3sin(θ4-θ5+θ6)
(2)
(3)
對柔索牽引式機器人機構的運動學、動力學方程求解,可計算出mL3和mR3。柔索牽引式機器人的末端位姿構件的運動規律,得到柔索牽引式機器人的載荷輸出為
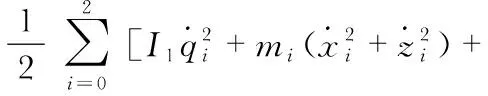
(4)
式中Ii為柔索牽引式機器人質心轉動慣量。結合機器人的力覺交互特征量,構建Lagrange動力學方程為
(5)
運用封閉矢量法進行機器人的運動學規劃,采用動態運動基元學習方法進行機器人的末端姿態力學參量調節和自適應控制[9]。
1.2 機器人的控制參量分析
在構建柔索牽引式機器人的運動學模型的基礎上,采用動態運動基元學習方法進行機器人的末端姿態力學參量調節和自適應控制[10],得機器人第i個組件的柔性力矩為
(6)
假設柔索牽引式機器人在運動中具有較大的速度和加速度,在移動慣性力矩的作用下,構建面向二自由度時滯系統的機器人機構控制函數為
S={(k,n),0≤k≤K,0≤n≤N}
(7)
結合柔性驅動分析方法,構建柔索牽引式機器人的電樞回路模型為
(8)
根據構建的柔索牽引式機器人的彈性流體動壓模型,采用多傳感器融合跟蹤方法進行柔索牽引式機器人的位姿信息采集和融合濾波分析[11],封閉矢量模型描述為
(9)
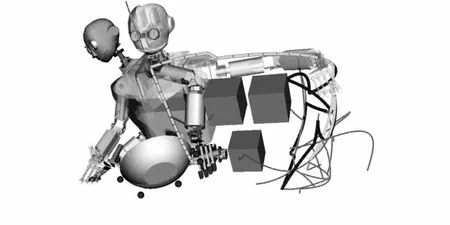
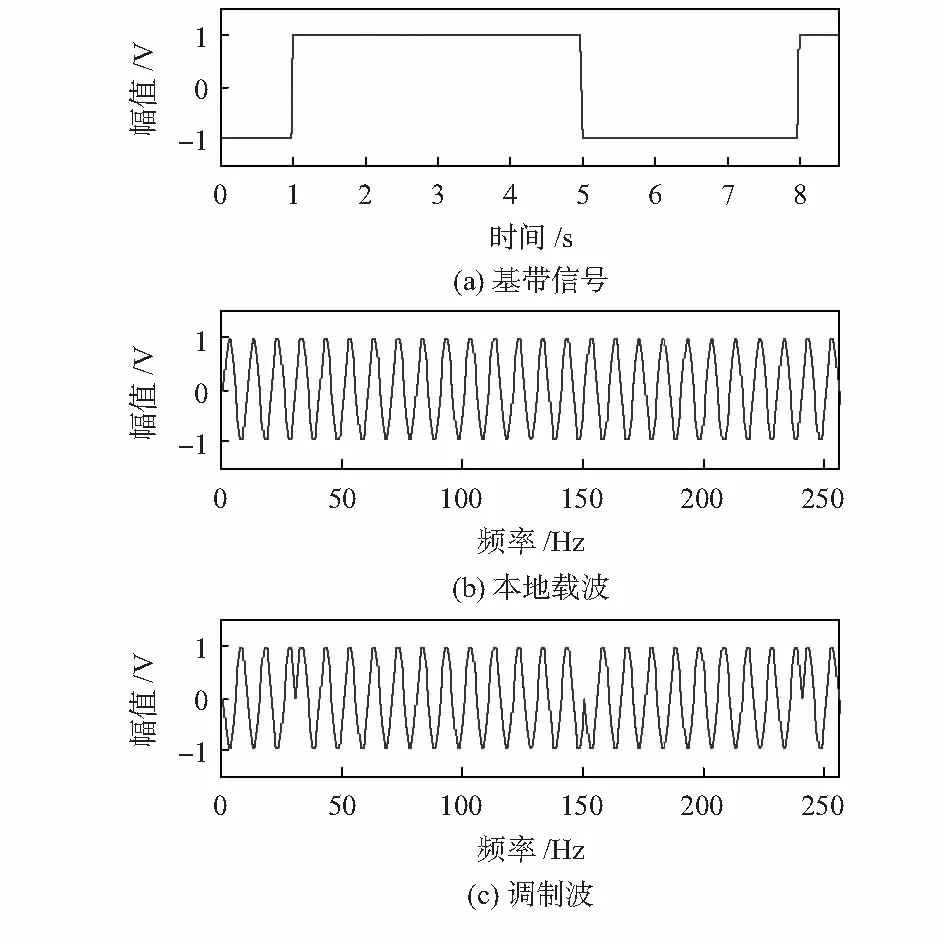
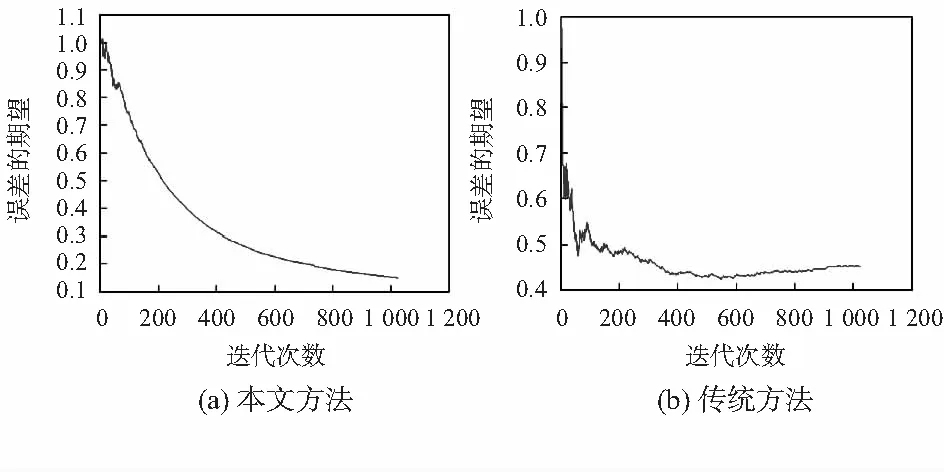
式中t1 在設計柔索牽引式機器人的7自由度運動學模型,采用動態運動基元學習方法進行機器人的末端姿態力學參量調節和自適應控制的基礎上,進行控制算法的優化設計,本文提出一種基于多傳感器參量融合的機器人姿態自適應調節方法。建立機器人的移動平臺和驅動單元進行的機器人姿態慣性參量調節,得到機器人的慣性力學場分布描述為 ZN=g·XN+WN (10) 式中ZN=[z1,z2,…,zN]H為末端位姿估計動力參數,XN=[x1,x2,…,xN]H為剛體間所有理想約束力,WN=[w1,w2,…,wN]H為機器人的全局運動干涉矢量。從k-1~k時刻k時刻進行柔索牽引機器人傳感信息融合跟蹤識別,采用穩態誤差跟蹤識別方法,得出振動響應的控制誤差為ex=x-xd,eθ=θ-θd,此時拉格朗日乘子作為未知變量,得到柔索牽引式機器人在零階模態下阻尼控制方程為 (11) 式中X=[θ,x,,分別為約束方程對應的拉格朗日傳遞函數,dx(t),dθ(t)為機器人各連桿之間的載荷勢能函數。 分析材料機械構件的載荷、屈服強度和應力強度之間的關系,得到柔索牽引式機器人機械性能傳導方程為 (12) 據上述參數融合結果,構建柔索牽引式機器人的彈性流體動壓模型,實現機器人姿態慣性參量調節和誤差補償。 采用模糊控制和雙目視覺動態跟蹤方法實現柔索牽引式機器人的優化控制設計,采用末端效應逆運動學分解方法對柔索牽引式機器人進行自主控制,得到機器人控制的位姿擴展運動學方程為pe=f(θ),建立機器人的移動平臺和驅動單元進行的機器人姿態慣性參量輸出的時滯跟蹤補償方程 (13) (14) 采用柔性驅動機構運動學和動力學交互控制方法進行組織結構的演變力學控制,結合機器人末端位姿調節算法進行機器人的姿態跟蹤識別,由此實現機器人姿態自適應調節控制。 為了驗證本文的算法在實現柔索牽機器人的末端位姿自適應調節和智能控制中的應用性能,進行仿真實驗,搭建硬件平臺,采用三軸電子羅盤LSM303DLH進行柔索牽引式機器人的姿態傳感數據采集,控制算法采用MATLAB 7設計,設計機器人的末端姿態參數采集的周期為0.12 s,姿態傳感信息采集的樣本值為2 000,機器人的姿態初始調節誤差為0.02,其他關鍵參數設定為:慣性力矩Mp=1.6×104kg,質量mr=1.13×104kg,轉動慣量R=2.05 m。進行機器人控制的姿態自適應調節仿真,得到機器人的姿態控制有限元分析仿真結果如圖2所示。 圖2 機器人的姿態控制有限元分析仿真結果 以圖2的柔索牽引式機器人有限元結構為研究對象,進行機器人的位姿動態跟蹤測量和末端位姿調節,得到位姿參數控制輸出結果如圖3所示。 圖3 機器人的姿態自適應調節控制輸出 分析圖3得知,采用本文方法進行機器人的姿態自適應調節控制,能有效實現參數修正及補償,得到最優的姿態參量,柔索牽引機器人末端位姿調節能力較好。為了對比性能,采用不同方法進行機器人姿態自適應調節控制,得到控制學習曲線對比如圖4所示。 圖4 姿態控制學習性能對比 對比圖4分析得知,本文方法進行柔索牽引機器人末端位姿調節控制的學習性能較好,收斂性較好,輸出姿態參量的誤差期望較低,機器人姿態自適應調節的魯棒性和抗擾動性得到大幅提升。 采用該方法進行機器人姿態自適應調節控制的輸出穩定性較好,末端姿態調整的誤差為較低,提高了機器人的抗擾動能力,輸出位姿的準確指向性得到提升,末端姿態測量和調節的平滑性和收斂性較好,在機器人控制中具有很好的應用價值。2 機器人姿態自適應調節控制優化
2.1 機器人姿態慣性參量調節和誤差補償
2.2 柔索牽引式機器人姿態自適應調節控制律優化
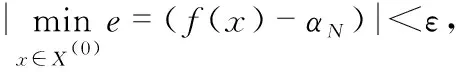
3 仿真實驗與結果分析
4 結 論

