基于ν-SVR的紙基納米金檢測Cr6+的濃度識別*

江亮亮， 羅小剛， 侯長軍， 錢 燁， 霍丹群

(重慶大學 生物工程學院生物流變科學與技術教育部重點實驗室，重慶 400044)

0 引 言

及時準確檢測出Cr6+含量至關重要[1,2]。納米金顆粒(gold nanoparticles,Au-NPs)因其獨特的光譜特性、較高的面容比和易于表面功能化被用作一種常用的檢測受體[3,4]，將Au-NPs修飾到紙基上可實現重金屬離子的精確檢測[5～7]。本實驗室的郭建峰等人[7]采用紙基納米金實現了Cr6+的濃度檢測，具有檢測限低、快速、穩定、特異性高等優點。但在基于紙基納米金的Cr6+的檢測中，如何由反應特征值自動進行濃度識別是一個亟待解決的問題。

近年來，采用人工神經網絡[8]、模糊推理[9]、支持向量機[10,11]、獨立分量分析和主分量分析[12,13]等智能信息處理算法進行濃度識別取得了長足進步。本文針對紙基納米金檢測Cr6+的特點，采用支持向量回歸(support vector regression,SVR)實現濃度識別，并與多項式非線性回歸識別和反向傳播(back propagation,BP)神經網絡識別效果進行對比，結果表明：基于SVR的濃度識別精度更高，能夠取得更好的識別結果。

1 紙基納米金制備

Au-NPs在較高的消光系數(108～1010(mol/L)-1cm-1)下具有很強的表面等離子共振吸收(surface plasmon resonance,SPR)效應[14]，發生肉眼可辨的顏色變化，可作為一種檢測比色傳感器。按文獻[15]所述方式，將牛血清蛋白(bovine serum albumin,BSA)添加到納米金溶液中，配成BSA-Au-NPs溶液。再按文獻[8]所述方式制備涂有TiO2的纖維素紙基(silanization-titanium dioxide modified filter paper,STCP)，該紙基上附著巰基和氨基，確保Au-NPs顆粒不易脫落。然后將BSA-Au-NPs溶液滴加到STCP上，用去離子水清洗后烘干，制成紙基納米金(BSA-Au-NPs/STCP)。最后將紙基放入混有HBr的待測溶液中水浴后取出烘干，采集紙基圖像，實驗紙基較對照紙基的顏色變化程度即可表征Cr6+的濃度。其化學變化原理如式(1)，紙基與Cr6+反應后，Au-NPs顆粒的數量和粒徑減少，導致顏色變淺，顏色變化程度與Cr6+濃度呈正相關

(1)

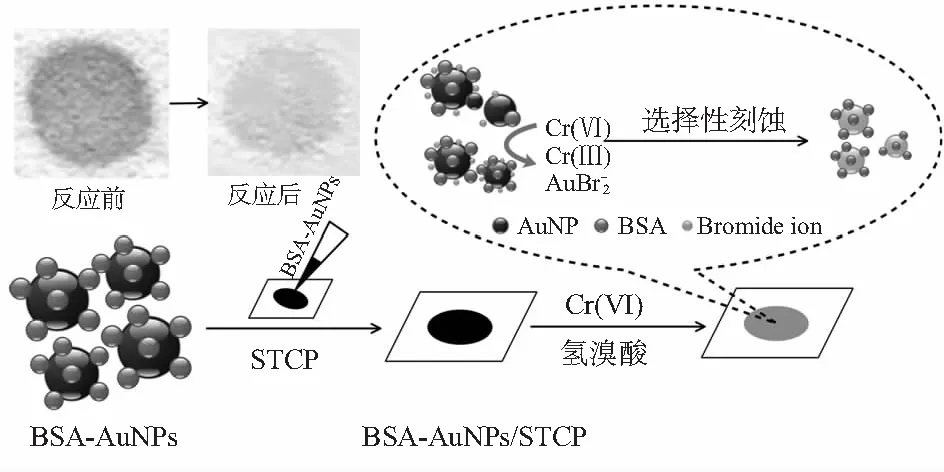
圖1 紙基納米金制備及檢測

2 ν-SVR模型

SVR[10]是基于結構風險最小化和統計學習理論的機器學習方法，其具有理論嚴謹、全局優化、訓練效率高和泛化性能好等優點。

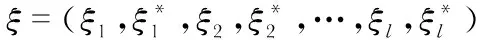
(2)

采用Lagrange乘子法對其進行優化，并引入核函數將原始樣本點映射到高維特征空間，其對偶問題為

(3)

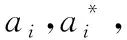
1)給定訓練樣本集T={(x1,y1),(x2,y2),…,(xl,yl)}∈(X,Y)，其中xi∈X=Rn,yi∈Y=R,i=1,2,…,l；

2)選擇適當的參數ν,C和核函數K(xi,xj)；

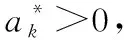
(4)

3 基于ν-SVR模型的Cr6+濃度識別

3.1 數據選取及處理

反應組紙基與對照組紙基的顏色差為分析所需的特征信息，為實現紙基納米金檢測Cr6+離子的濃度識別，選取25組實驗數據，如表1所示。

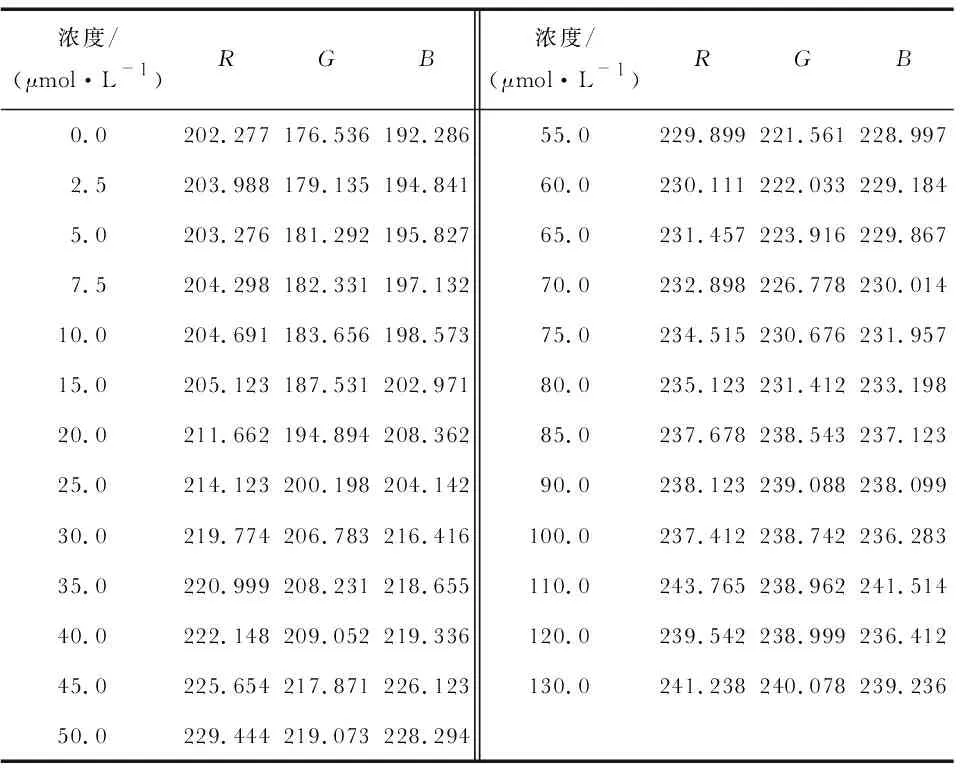
表1 紙基納米金的Cr6+檢測實驗數據

各濃度紙基的顏色信息減去濃度為0時的紙基顏色信息即為顏色的變化程度，此時樣本數據包含濃度、R分量變化值ΔR,G分量變化值ΔG,B分量變化值ΔB，共24組數據，n=24，其中ΔR,ΔG,ΔB為自變量，濃度為因變量。

數據歸一化效果對預測結果有較大影響，選用全序列法實現數據歸一化

(5)

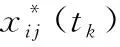
將歸一化數據中的2/3作為訓練集進行訓練，1/3作為測試集進行驗證。具體選擇方式為從第3個數據開始，每間隔2個數據抽取1個數據作為測試集，余下的數據作為訓練集，此時訓練集共計16組數據，測試集共計8組數據。

3.2 最優參數選擇

采用6—折交叉驗證，在給定ε=0.001的前提下，懲罰系數C的取值范圍為2-10～210，核函數參數g的取值范圍為2-10～210，ν的取值范圍為2-20～20，均以指數變動0.2作為步長，通過C，g，ν的不同取值，找出交叉校驗誤差最小時對應的那一組參數即為最優參數，RBF核函數，Sigmod核函數和多項式核函數的c,g,ν分別為85.289 3，5.076 2，0.283 1；147.199 3，0.020 6，0.856 3；50.231 2，10.442 9，0.703 2。

采用訓練集以不同核函數及對應的最優參數對模型進行訓練，將擬合結果分別投影到R空間、G空間和B空間進行展示。可知，RBF核的ν-SVR模型擬合的回歸數據與原始數據重合率最高，擬合效果最好如圖2所示。3種不同內核的模型的相關性R2分別為RBF核函數為0.997 5，Sigmod核函數為0.911 7，多項式核函數為0.969 3。

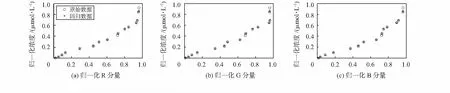
圖2 RBF核函數對應的ν-SVR模型對訓練集的擬合效果

可知，RBF核函數的模型擬合效果明顯優于Sigmod核函數和多項式核函數，表明RBF核函數的模型其訓練精度較高，訓練效果較好。因此，ν-SVR模型的最優參數為：選用RBF核函數，且C=85.289 3，g=5.076 2，ν=0.283 1。以最優參數完成模型訓練，即可對測試集進行預測。

3.3 識別效果評價

為驗證ν-SVR模型對濃度的識別效果，采用相同的訓練集和測試集，與多項式非線性回歸識別方法和BP神經網絡識別方法進行對比,如表2。

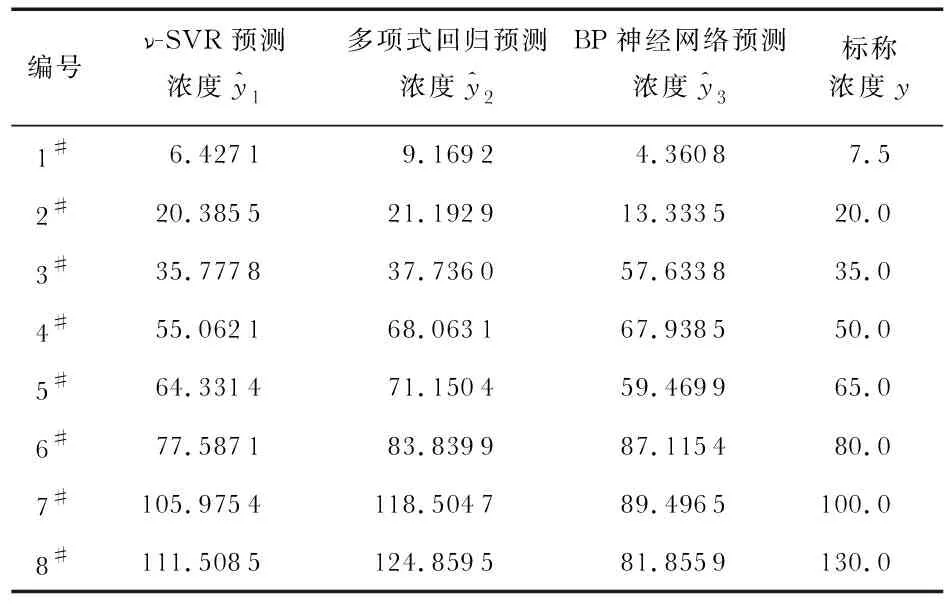
表2 測試集預測結果 μmol·L-1

平均相對誤差(average relative error,ARE)表征了預測濃度與真實濃度之間的誤差大小，有

(6)

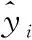
可知，ν-SVR模型對測試集的識別ARE為6.603 1 %、多項式非線性回歸的識別ARE為13.608 2 %、BP神經網絡的識別ARE為30.084 1 %，其中，ν-SVR模型的識別ARE最低，識別精度最高，識別效果最好。即采用ν-SVR模型可實現紙基納米金檢測Cr6+濃度的精確識別。

4 結 論

本文將SVR應用到當前的研究熱點即，紙基納米金檢測中，對Cr6+濃度進行預測，根據最終的識別結果對比分析，相較多項式回歸分析、BP神經網絡，SVR具有更高的預測精度和較強的泛化能力，對紙基納米金的檢測研究具有重要理論價值和應用前景。