鐵基超導體的掃描隧道顯微鏡研究進展?
顧強強 萬思源 楊歡 聞海虎
(南京大學物理學院,超導物理與材料研究中心,南京 210093)
鐵基高溫超導體自2008年發現以來,對其超導電性的研究一直是一個熱門的課題.掃描隧道顯微鏡能夠在原子尺度進行表面形貌和隧道譜測量,從微觀角度研究電子態密度的信息,是研究超導的重要譜學手段.近年來,在鐵基超導電性方面,掃描隧道顯微鏡實驗已經積累了一些有價值的結果,本文進行了總結介紹.鐵基超導體是多帶多超導能隙的超導體,不同材料的費米面結構有很大的變化.掃描隧道顯微鏡證明,同時有電子和空穴費米面最佳摻雜的鐵基樣品超導能隙結構是無節點并帶有能隙符號變化的s±波.而進一步的實驗發現在沒有空穴費米面的FeSe基超導體中也存在能隙符號的相反,對統一鐵基超導體的配對對稱性提供了重要實驗證據.此外,掃描隧道顯微鏡在研究鐵基超導體的電子向列相、淺能帶特性、可能的拓撲特性方面,提供了重要的實驗數據.本文對上述相關內容進行了總結,并做了相應分析和討論.
1 引 言
鐵基高溫超導體自2008年發現[1]以來,部分材料的超導臨界溫度Tc超過了麥克米蘭極限[2](≈40 K),使得鐵基超導體成為除銅氧化物以外的第二類非常規高溫超導體家族[3].同時,高Tc和毗鄰的反鐵磁相也表明鐵基超導體機理無法在Bardeen-Cooper-Schrief f er的電聲耦合(BCS理論)框架下進行理解,說明鐵基超導體屬于非常規超導之列.在鐵基超導體中,鐵原子的有效磁矩雖然不大,但是由它引起的反鐵磁漲落和超導電性的產生密切相關[4].作為一個典型的多帶超導體,鐵基超導存在多能隙的特性,而且隨著摻雜能帶和能隙結構發生很大的變化,使得這個系統的超導電性變得非常復雜[5].加之相圖中的結構相變、反鐵磁(antiferromagnetic,AFM)相變和向列相(nematic phase)的出現,給理解鐵基超導的超導起源研究帶來了更多挑戰[6].
掃描隧道顯微鏡(scanning tunneling microscope,STM)能夠從原子尺度研究樣品表面態密度的信息,具有很高的空間、能量分辨率,還能得到一定動量空間的信息,因此在研究超導材料的性質,尤其是配對對稱性方面有著很強的優勢.在鐵基超導物理研究的十年中,STM領域取得了一系列重要進展,對理解鐵基高溫超導機理等問題有很大的幫助.本文對STM在鐵基超導電性和奇異電子態方面的工作進行總結:簡要介紹了STM的工作原理及其對超導研究的作用;總結了STM在不同費米面結構的鐵基超導體中對超導配對對稱性的研究工作;介紹了一些與超導相關的奇異電子態.
2 STM在超導研究中的應用
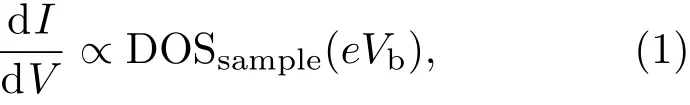
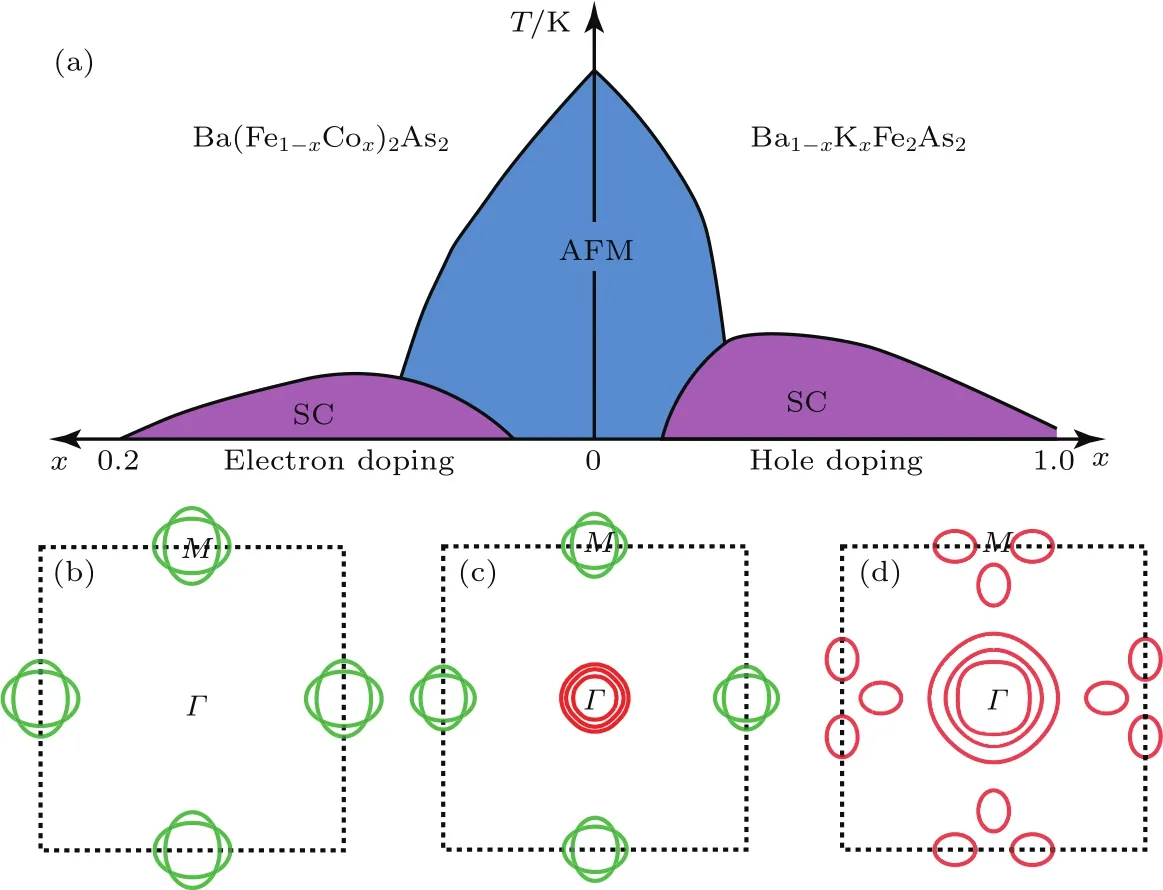
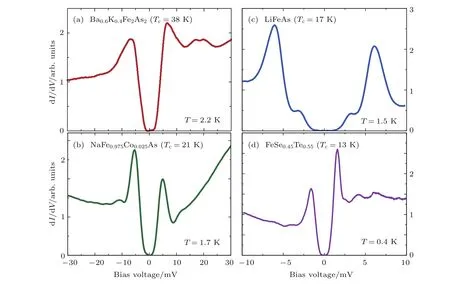
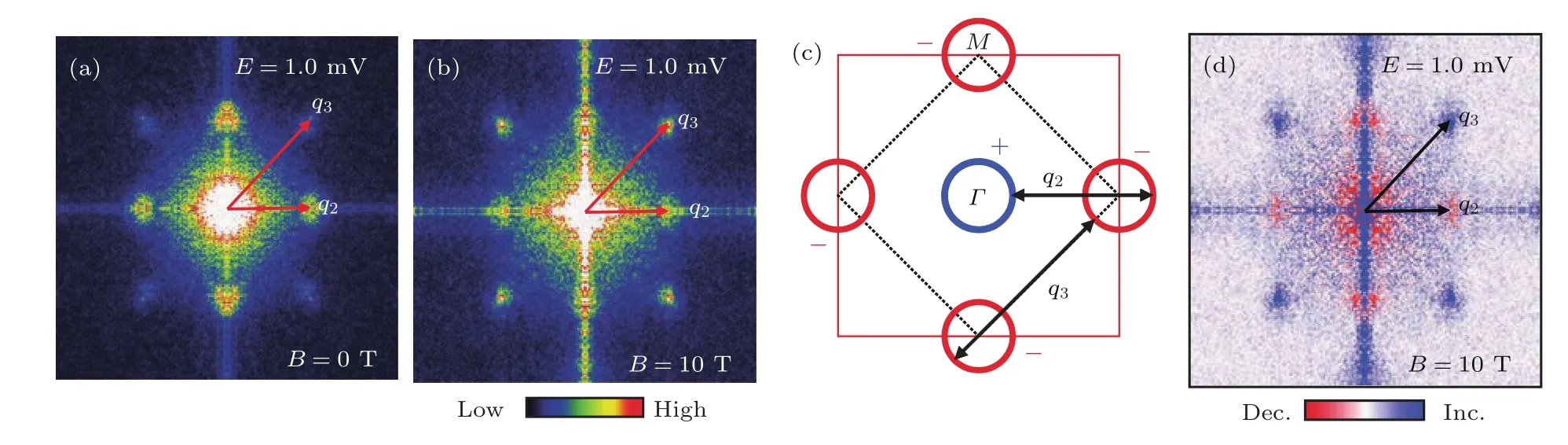
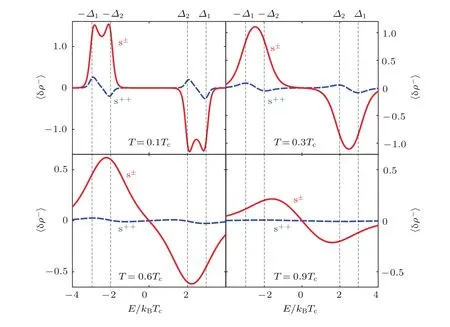
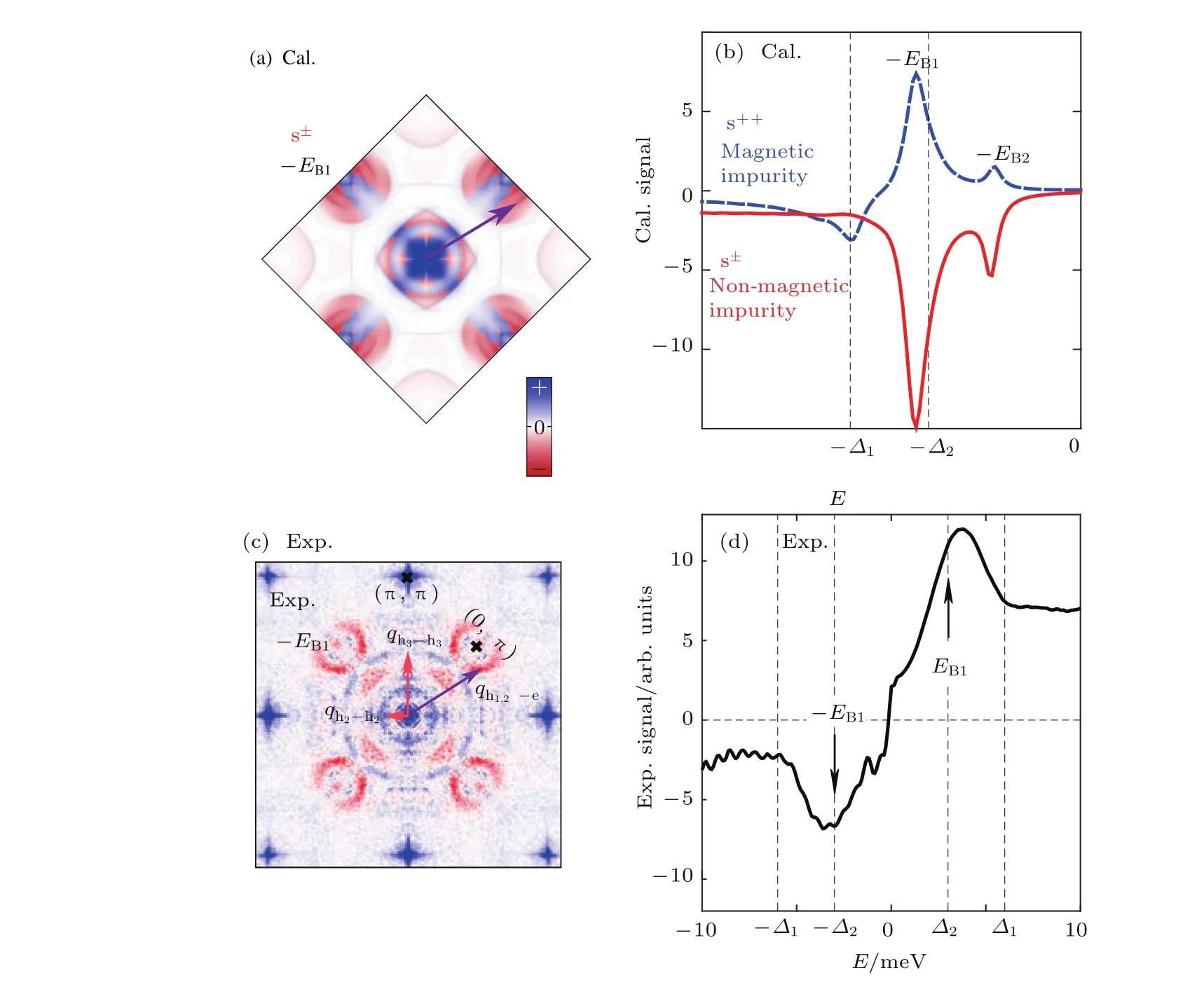
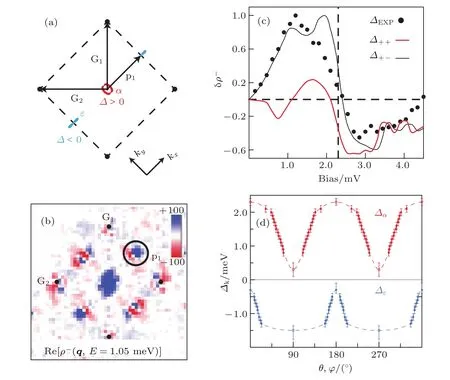
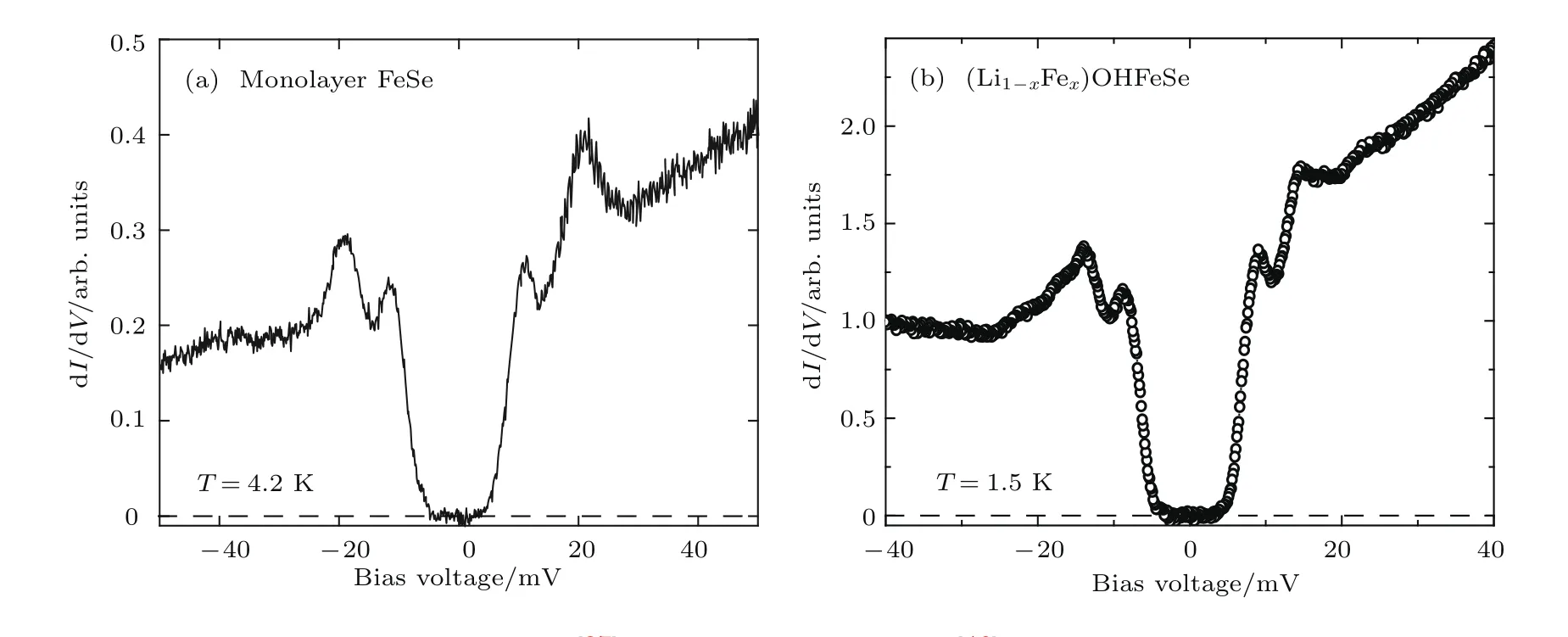
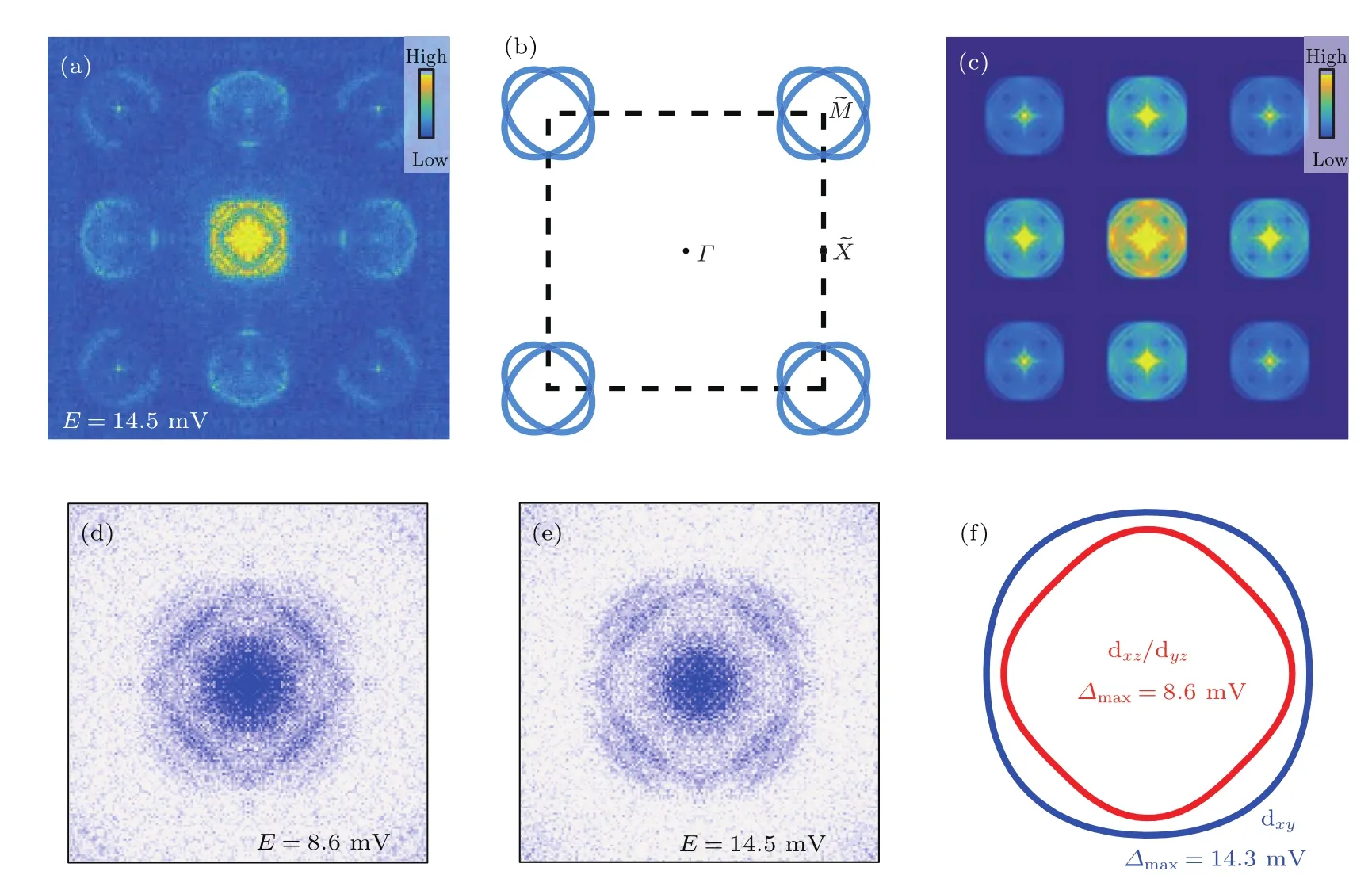
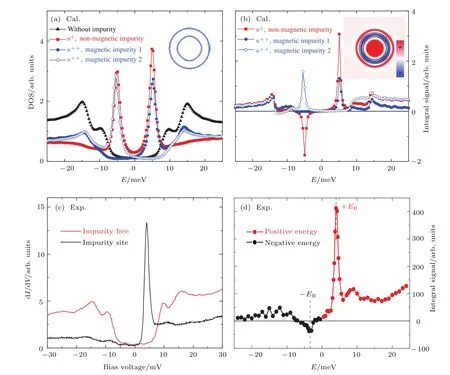
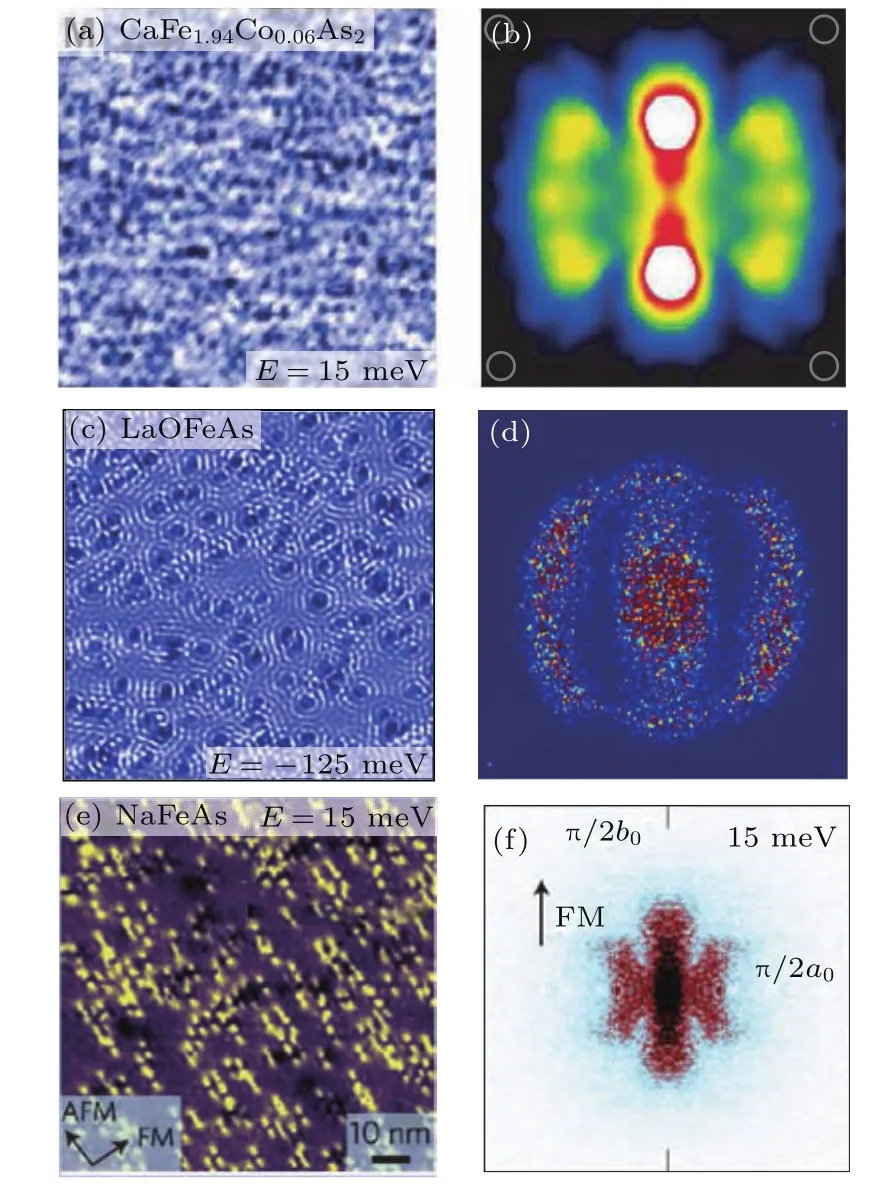
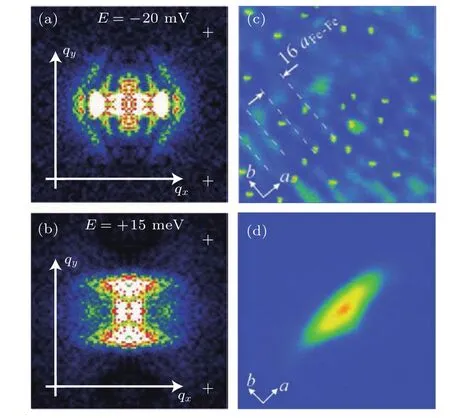
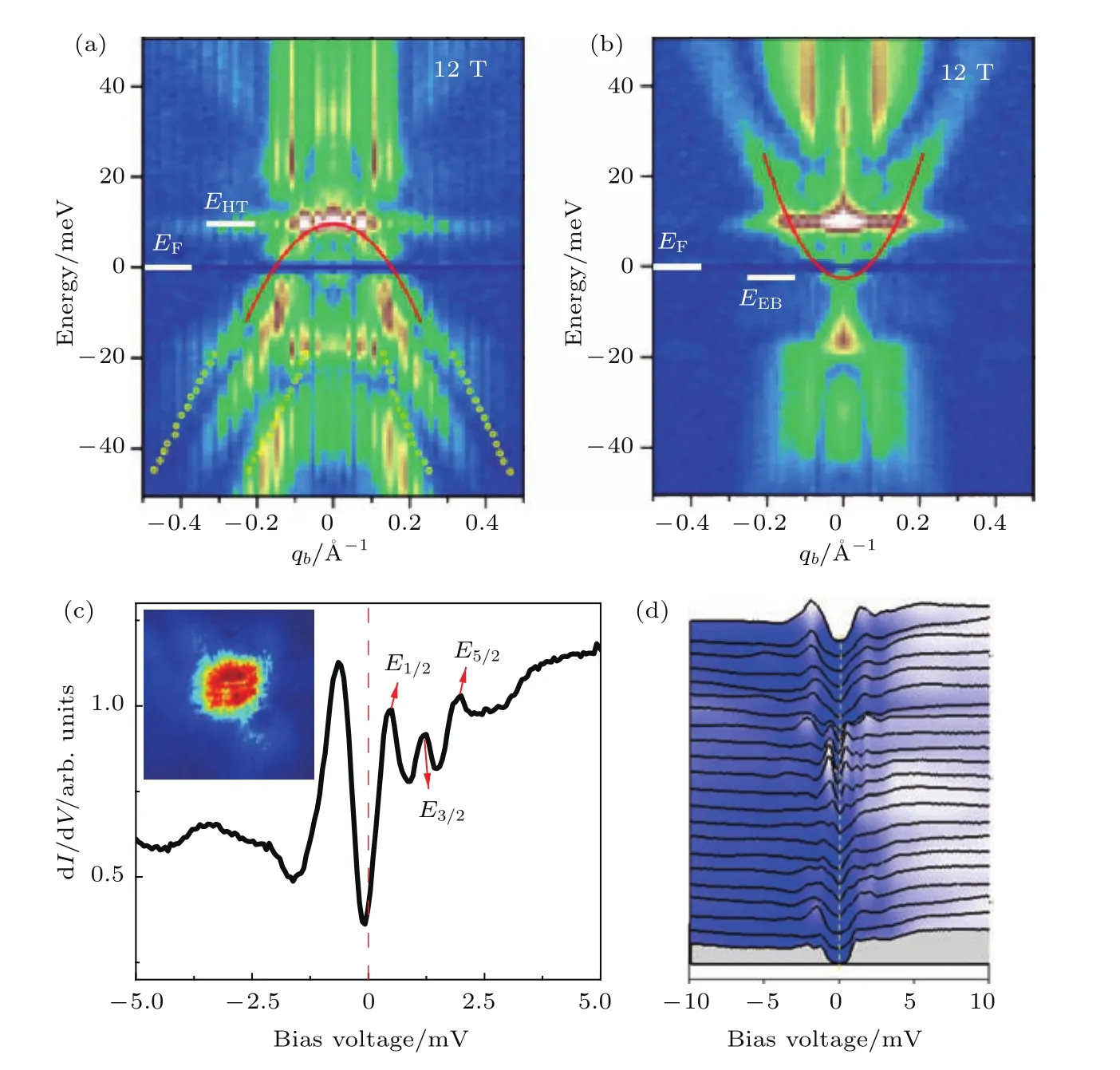
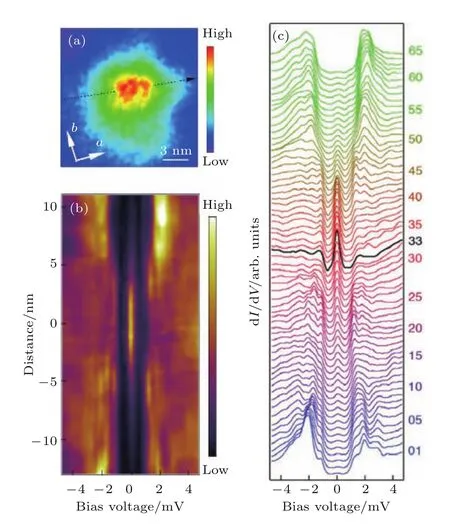
STM是利用量子力學的隧道效應,即當金屬針尖和樣品非常接近時,加上中間的真空薄層,形成“針尖-真空-樣品”隧道結,電子在針尖和樣品之間發生單電子量子隧穿效應.在隧道結兩邊加上電壓(bias voltage,Vb),可以測量隧道電流(tunneling current,It).由于針尖尖端可以處理單原子或幾個原子,因此該技術具有很高的空間分辨率,能夠直接測量樣品表面的原子形貌.另外在保持針尖樣品距離恒定,通過掃描加在針尖和樣品之間的電壓,同時測量隧道電流和微分電導(dI/dV),能夠獲得樣品表面微分電導隨電壓的變化關系(即隧道譜),因此掃描隧道顯微鏡也被稱為掃描隧道譜儀(scanning tunneling spectroscopy,STS).如果假設金屬針尖的電子態密度(density of states,DOS)在一定電壓范圍內隨能量變化不大,簡化隧穿矩陣元效應,那么測量得到的微分電導將正比于樣品在此能量下(eVb,e為元電荷)表面的電子態密度[7],即這里的DOSsample即為樣品在離費米能E=eVb時的電子態密度.這一譜學手段對于超導研究來說非常重要.基于BCS理論,兩個電子配對形成庫珀對,庫珀對凝聚形成超導.當電子形成庫珀對后,體系的動能有所增加而勢能會下降得更多,使總的能量得到降低.在超導態,單電子或準粒子激發滿足Bogoliubov色散,即Ek=而εk=}2k2/(2m)?EF,εk是從費米能算起的動能,?是超導能隙.不考慮散射時,零溫極限下準粒子的態密度將在超導能隙內(?? 材料的費米面通常用角分辨光電子譜(angleresolved photoemission spectroscopy,ARPES)來測量,它同時有動量和能量分辨.而STM/STS通過對微分電導在實空間分布的測量也可以得到動量空間的信息.周期性晶格中的電子波函數可以用布洛赫波來描述,當晶格中存在雜質、缺陷或者晶界時,這些電子會被散射導致弗雷德爾(Firiedel)振蕩,在實空間產生局域態密度的調制,或稱為駐波.通過STM測量某個能量E下空間位置的微分電導變化ρ(r,E),即測量樣品表面的準粒子相干(qausiparticle interference,QPI)圖像,而該圖像可以近似地看作樣品表面電子態密度的分布.如果對ρ(r,E)進行傅里葉變換(Fourier transform),得到ρ(q,E),這是一個q空間的復數函數,其模值|ρ(q,E)|稱為FT-QPI(Fourier transformed-QPI)圖案.從動量空間理解,此散射過程可以理解為電子從動量k態被彈性散射到k′態,會造成FTQPI圖案上q=k′?k位置處的斑點.散射斑點的強度近似正比于這兩點的態密度乘積,即DOS(k,E)·DOS(k′,E),通常被稱為聯合態密度(joint DOS).在q空間某點得到的ρ(q,E)圖案是所有動量差q=k′?k的散射的累積.對于在正常金屬上測量得到的FT-QPI圖案,除了噪音、雜質態和布拉格散射的信號,主要是態密度較高的費米面波矢之間的散射信號.因此對于正常金屬,FT-QPI圖案可以由對費米面圖像的自關聯(selfcorrelation)操作得到模擬的圖像,然后和實驗測量的FT-QPI圖案進行比較.但是需要注意的是,FT-QPI圖案得到的是q空間的信息,而不是直接的動量空間的信息,且不能反映費米面在動量空間的具體位置,它需要一定的反演推導才能得到費米面的信息. 對于超導體來說,超導態激發的是Bogoliubov準粒子.Bogoliubov系數,即庫珀對未占據和占據±k態的概率幅表達式為: 由上面的公式可知,Bogoliubov準粒子不僅帶有動量和能量信息,還攜帶了超導序參量即能隙的信息.而Bogoliubov準粒子也會被散射中心散射,由費米黃金定則,在簡單模型下散射的強度不僅僅正比于散射初態和末態的態密度,還與超導態的相干因子項相關[7].(4)式中對于非磁性散射取“?”號,對于磁性散射取“+”號.因此,對超導態的QPI測量是一個信息豐富的實驗技術,可以從中提取超導準粒子的動量和能量信息,甚至還可以得到超導序參量即能隙的信息. 圖1 鐵基超導體的摻雜相圖示意圖和不同材料的費米面示意圖 (a)從BaFe2As2母體出發分別進行電子和空穴摻雜的相圖示意圖;(b)FeSe單層膜、Li1?xFexOHFeSe等材料的費米面結構示意圖;(c)最佳摻雜Ba1?xKxFe2As2,BaFe2?xCoxAs2,NaFe1?xCoxAs等材料的費米面結構示意圖;(d)重度空穴摻雜KFe2As2材料的費米面結構示意圖Fig.1.Schematic plot of the phase diagram and Fermi surfaces of iron-based superconductors:(a)The schematic phase diagram of BaFe2As2family by hole doping and electron doping;(b)schematic Fermi surfaces of monolayer FeSe or Li1?xFexOHFeSe;(c)schematic Fermi surfaces of optimally doped Ba1?xKxFe2As2,BaFe2?xCoxAs2or NaFe1?xCoxAs;(d)schematic Fermi surfaces of heavily hole-doped KFe2As2. 鐵基超導體的材料體系眾多,通過摻雜可以改變樣品的費米面結構,并得到不同Tc的超導體.圖1(a)顯示了以BaFe2As2為母體分別做空穴摻雜(Ba位摻入K)和電子摻雜(Fe位摻入Co)后的相圖示意圖.其中,BaFe2As2母體是一個反鐵磁壞金屬而并不超導,在一定溫度下發生AFM相變,同時伴隨四方到正交的結構相變;隨著摻雜增加,體系的巡游性增強,反鐵磁相得到壓制,AFM相變的奈爾Neel溫度減小,超導出現,并在一定摻雜量出現Tc最大值;隨著摻雜進一步增加,超導被破壞,Tc降低.鐵基超導體的超導相與反鐵磁相近鄰,兩者相互競爭,反鐵磁消失的量子臨界點附近對應著高Tc超導相,這一現象強烈暗示反鐵磁漲落很可能是鐵基超導體非常規配對的主要媒介.摻雜影響著鐵基超導體的Tc,而且對材料的費米面結構有很大的改變.一些典型鐵基材料的費米面示意圖如圖1(b)—(d)所示,在這些圖中,紅線表示空穴型費米面,綠線表示電子型費米面.對于一些FeSe基的超導材料,如FeSe單層膜、Li1?xFexOHFeSe等材料,因為在Γ點附近的空穴型能帶沉到了費米能以下[8?13],使得布里淵區中心缺失了空穴型費米面,僅在四邊M點附近留下了電子型費米面,其費米面結構示意圖如圖1(b)所示.圖1(c)為最佳摻雜的鐵基樣品(如最佳摻雜Ba1?xKxFe2As2,BaFe2?xCoxAs2,NaFe1?xCoxAs等)的費米面示意圖,布里淵區中心Γ點附近為空穴型費米面,M點附近為電子型費米面.圖1(d)是KFe2As2材料的費米面結構示意圖,由于重度空穴摻雜的緣故,原本Γ點附近的空穴型費米面變得很大,而在M點附近留下“花瓣狀”的空穴型費米面[14]. 在鐵基最佳摻雜的樣品中,電子和空穴費米面大小接近,如圖1(c)所示,此時電子與空穴之間的散射波矢為(0,π).實驗測量發現[15]自旋極化率在反鐵磁特征波矢(0,π)處,在超導臨界溫度之下出現共振峰值,證明鐵基超導的磁配對起源,結合理論理解,說明電子和空穴費米口袋的超導能隙符號會出現反轉[16],形成所謂的s±配對態[17,18].這時材料的超導能隙函數在每個費米口袋上仍具有s波對稱性,而±表明電子和空穴口袋的超導能隙函數存在反號.由于鐵基超導體是一個多軌道系統,另一種觀點認為適度的電聲相互作用能夠增強Fe的3d軌道漲落[19],兩電子仍可以通過聲子為媒介形成配對,導致s++配對態,其超導能隙函數的符號在整個布里淵區不會產生變化.上述兩種配對方式都是無能隙節點的s波超導體,區別在于電子和空穴口袋上的超導能隙是否有變號行為.對于能隙函數沒有節點這一問題,可以由STM測量到的隧道譜很好地證明.如圖2所示,在一些既有電子又有空穴型費米面的鐵基超導體中,隧道譜在零能附近完全沒有正常態的準粒子態密度,隧道譜在能隙之間的底部也呈現出英文字母“U”的形狀.但是,能隙相反這個問題卻不容易直接證明.這里需要注意的是,圖2所示的隧道譜在正負能量有些不對稱,相干峰等也不對稱,這可能是由多帶情況下的電子和空穴能帶都比較淺,而且費米能不一樣造成的. 圖2 同時有電子空穴費米面的幾個典型鐵基超導體表面沿c-軸方向測量的隧道譜Fig.2.Tunneling spectra measured on the surfaces of some typical iron-based superconductors with both electron and hole Fermi pockets,the tunneling current is injected along c-axis. Hanaguri等[20]在Fe(SeTe)上進行了加場前后的QPI測量,主要結果如圖3所示.Fe(SeTe)同時有電子和空穴型費米面,費米面大小相似,在FT-QPI圖案上得到的主要散射為電子-空穴口袋間的q2散射和電子-電子口袋間的q3散射,如圖3(c)所示.如果考慮到電子和空穴費米口袋上的能隙符號相反,即s±配對,那么q2對應異號能隙費米口袋之間的散射,q3對應同號能隙費米口袋之間的散射.如圖3(a)所示,在測量得到的零場下FT-QPI圖案中可以看到,q2散射斑紋較強,而q3散射斑紋較弱.簡單地從(2)式和(3)式出發,當能隙符號相反時,Bogoliubov系數uk和vk反號,而能隙符號相同時uk和vk同號.而樣品中廣泛分布的缺陷或者雜質作為非磁性雜質對Bogoliubov準粒子進行了散射,根據(4)式定義,此時相干因子I(k,k′)=|uku?vkv′|2.因此,對于同號散射相干因子較小,而異號散射相干因子較大,這是電子空穴費米面能隙符號相反的第一個證據.當加了10 T磁場后,磁通芯子可以認為是磁性散射中心,同上面的分析,序參量異號的散射會被抑制,而同號散射會被增強.實際測量的結果如圖3(d)所示,與預期相符合,因此證明了Fe(SeTe)體系中電子和空穴型口袋間的能隙符號相反.但是,由于q3散射斑點和布拉格點重合,特征散射斑紋沒有外圍圈,該結論受到一些理論上的質疑[21].其中,關于特征散射斑紋沒有外圍圈,進一步的研究解釋為Fe(SeTe)中電子和空穴費米口袋比較小,再加上費米口袋有一定的動量空間寬度,使得散射特征圖案沒有出現外圍圈,而保留有中間很亮的斑[22]. 圖3 Fe(SeTe)磁場下FT-QPI圖案中不同散射斑紋強度的變化 (a),(b)分別在零場和10 T磁場下得到的FT-QPI圖案;(c)Fe(SeTe)費米面以及主要的口袋間散射通道示意圖;(d)圖(b)減圖(a)得到的FT-QPI受到磁場影響的結果,紅色為信號減弱,藍色為信號增強[20]Fig.3.Magnetic f i eld dependent intensity of dif f erent kinds of characteristic scattering spots on FT-QPI patterns measured in Fe(SeTe):(a),(b)FT-QPI patterns measured at 0 T and 10 T,respectively;(c)a schematic plot of Fermi surface and inter-pocket scatterings in the momentum space;(d)the intensity dif f erence of characteristic scattering spots by subtracting(a)from(b)[20]. 圖4 非磁性銅雜質誘導的能隙內束縛態 (a)STM測量得到Cu摻雜原子上方表面Na原子的形貌;(b)摻雜Cu原子對表面Na原子影響的示意圖;(c)沿圖(a)中箭頭測量的一系列隧道譜;(d)減去遠離雜質點2 nm的隧道譜得到的微分電導譜差隨空間的演化[28]Fig.4.In-gap bound state induced by the non-magnetic Cu impurity:(a)The topography of the Na atoms on the surface above a Cu impurity;(b)illustration for atoms near a Cu impurity site;(c)tunneling spectra measured along the arrowed line shown in(a);(d)the dif f erence tunneling spectra by subtracting the spectra with that measured 2 nm away from the Cu site[28]. 非磁性雜質產生的束縛態也可以用來判定超導能隙函數的形式.從著名的安德森理論[23]出發,對于沒有能隙符號反轉的超導體,磁性雜質與巡游電子之間產生磁交換作用,導致配對電子的自旋翻轉,從而破壞超導,并產生費米能附近的Yu-Shiba-Rusinov雜質共振態[24];而非磁性雜質很難對普通s波超導體產生實質性破壞作用,有限的勢散射無法對電子配對散射過程產生明顯影響,不會形成費米能附近的雜質共振態[24].而對于有能隙符號反轉的超導體中,如d波銅氧化物超導體中,非磁性雜質會造成能隙內的很強的雜質態峰[25].在鐵基超導體s±配對態下,理論計算表明,合適的非磁性雜質散射勢(~1 eV)也會產生雜質束縛態的峰[26].通常認為,鐵基超導體中的鐵離子是沒有磁性的,而鈷、鎳等摻雜原子進入晶格形成離子態后,其性質和鐵離子態是接近的,因為多余的d電子加入到巡游電子之列,因此通常也被認為沒有磁性.實驗上,當非磁性雜質的散射勢比較小時,例如Na(Fe1?xCox)As中的Co雜質,雜質誘導的雜質態將靠近超導相干峰,在零能附近不能觀察到雜質束縛態[27].從最佳摻雜的Na(Fe1?xCox)As材料出發,進一步摻入Cu雜質,利用磁化測量判定了銅原子是非磁性或弱磁性雜質[28].利用STM可以找到摻雜的Cu原子所在的位置,測量到的Cu原子上方表面Na原子形貌如圖4(a)所示,結合原子分布示意圖4(b),可以判定高亮雙錘形的亮斑中心位置下方應該是一個摻雜的Cu原子.隧道譜的測量表明,Cu雜質對隧道譜在能隙內的譜形影響很大,如圖4(c)所示.而當把遠離雜質點測量的隧道譜作為背景減掉,可以得到能量依賴的微分電導差,如圖4(d)所示,從圖中可以清晰地看到非磁性雜質Cu原子誘導出了能隙內的雜質態,并與基于s±配對下的理論計算結果一致,作為一個較為堅實的實驗證據,證明了該材料的s±超導配對的對稱性[28]. 前面提到,超導Bogoliubov準粒子含有超導序參量的信息,在FT-QPI散射強度的計算過程中需要考慮相干因子的作用.傅里葉變換得到的復函數ρ(q,E),不僅有強度即|ρ(q,E)|,還有相位θq,E,即ρ(q,E)=|ρ(q,E)|eiθq,E. 而對于Bogoliubov準粒子散射過程,θq,E也含有超導序參量的信息.幾位理論學家Hirschfeld,Altenfeld,Eremin和Mazin提出了相位敏感的QPI分析方法[29],這里把這一方法簡稱為HAEM的QPI方法.該方法考慮一個非磁性雜質(散射勢為U)放置在實空間QPI圖像的中心位置,相位參考量是FT-QPI正負能量的反關聯部分,即ρ(q,+E)?ρ(q,?E).理論上,當雜質在實空間圖像中心且實空間圖像是中心對稱時,如果做傅里葉變換,根據傅里葉變換的定義,FT-QPI的信號ρ(q,E)將為實數[22].在此情形下,對于兩個費米面兩個超導能隙?1和?2(|?1|>|?2|)的情況,對包含兩個費米面之間散射波矢的q空間區域S進行積分,可以得到半定量的表達式[29]: (5)式中Re代表實部,Im代表虛部.從(5)式可以看出,如果?1?2>0,即對于兩個費米面上的超導序參量同號的s++配對態,δρ?(E)在兩個能隙之間(|?2| 圖5 HAEM方法理論計算得到的不同超導能隙結構和不同溫度下的相位敏感QPI信號δρ?(E)[29]Fig.5.Calculation results of phase-referenced QPI signal δρ?(E)in superconductors with dif f erent gap symmetries at dif f erent temperatures by HAEM’s method[29]. 圖6 DBS-QPI方法基于LiFeAs能帶結構理論計算和在LiFeAs樣品上實驗測量的相位參考的QPI結果[32,33]Fig.6.Calculation and experimental results of phase-referenced QPI signal δρ?(E)in LiFeAs by DBS-QPI method[32,33]. 最近,Chi等[32,33]又提出了新的相位參考QPI方案,該方案基于實空間QPI圖像中心的單雜質產生的能隙內束縛態,簡稱為DBS-(defect bound state)QPI方法.該方法以正負能量的FT-QPI信號為幅值,而正能量下的相位θq+E為參考相位,定義正負能下的相位參考量表達式為[32]:根據(6)式的定義,gpr(q,+E)始終是正值,而gpr(q,?E)是真正相位參考的量.該文獻指出,對于無磁性雜質在s±配對的情況下,散射前后波矢所對應的能隙符號相反,對應的散射相位參考項cos(θq,?E? θq,+E)是?1;而對于s++配對,其值是+1.這里的能量是指束縛態峰值的能量.該結論是否具有廣泛性還未見理論推導.不過作者以LiFeAs材料為對象進行了數值計算,計算結果如圖6(a)和圖6(b)所示.計算LiFeAs上的雜質在能隙內產生了兩個束縛態,能量位置分別在EB1和EB2.圖6(a)是對相位參考項gpr(q,?EB1)的計算結果,其中箭頭所示的斑紋為電子和空穴口袋之間的散射區域,主要為負值.對于gpr(q,E)在上述散射區域進行積分得到gpr(E),結果如圖6(b)所示.可以明顯地看到,s±配對下的非磁性雜質和s++配對下的磁性雜質,gpr(E)的結果有很大的差別:對于磁性雜質,同號超導能隙費米口袋之間的散射在雜質束縛態能量處的gpr(?E)信號為正;而對于非磁性雜質,異號超導能隙費米口袋之間的散射在雜質束縛態能量處的gpr(?E)信號為負.這里需要注意的是,對于s++配對的超導體,非磁性雜質不會出現能隙內明顯的束縛態的峰,因此未做相關討論.當雜質在中心且實空間圖像中心對稱的理想情況下,ρ(q,E)為實數,θq,E取0或π,因而相位差θq,?E?θq,+E也為0或π.根據數值計算可以得到這樣的結論:對于非磁性雜質造成的s±配對費米口袋之間的散射,正負能量的散射相位相反,即|θq,?E? θq,+E|= π.Chi等[33]還在實驗上對LiFeAs的QPI進行了相關測量和分析,結果如圖6(c)和圖6(d)所示,可以發現此時相位參考量gpr(?E)在其中一個束縛態能量?E=?EB1附近有個負值的峰,與s±配對下的非磁性雜質結果定性一致,他們確定LiFeAs材料中的電子空穴口袋能隙存在反號[33].而進一步基于(7)式,在多雜質且無明顯雜質束縛態的情形下,DBS相位參考方法也能用來有效判定其他非常規超導材料的配對對稱性[22,34]. 圖7 不同實驗組測量的FeSe單晶超導隧道譜 (a)FeSe多層膜上測量的結果[39];(b)FeSe單晶上測量的結果[40];(c)更低溫度下FeSe單晶的數據[30]Fig.7.Tunneling spectra measured on FeSe by di ff erent groups:(a)Tunneling spectra measured on FeSe thick fi lm[39];(b)tunneling spectrum measured on FeSe single crystal[40];(c)tunneling spectrum measured on FeSe single crystal at a lower temperature[30]. FeSe是鐵基超導體中具有最簡單結構的材料[35],臨界溫度在9 K左右,但是該材料和FeAs體系材料不一樣的是,在90 K左右僅僅有結構相變,但是在超導轉變溫度之上卻未發現反鐵磁相變.FeSe單晶在加壓后最高Tc可達37 K[36],而在FeSe單層膜中發現了較大能隙[37],直接的電阻測量發現Tc甚至超過了50 K[38].上述這一系列新奇的物理現象使得FeSe這一材料備受關注.對于FeSe厚膜材料[39]和單晶材料[40]的早期STM隧道譜研究發現,在費米能附近,隧道譜譜形呈現“V”形,如圖7(a)和圖7(b)所示,說明該材料中可能存在能隙節點.但是隨后的一些實驗,如低溫比熱[41,42]、微波光導[43]、熱導[44]、穿透深度[45]等測量,都表明FeSe單晶是一個無能隙節點但存在能隙極小的多能隙體系. 2017年,Sprau等[30]將測量溫度降到280 mK,發現零微分電導不只是發生在費米能位置,而是一個很小的能量范圍,如圖7(c)所示,并確認能隙最小值&150μeV,排除了有能隙節點的d波配對對稱性.他們還進行了更為精細的QPI測量,并用HAEM的相位參考方法來判定超導能隙正負號是否發生變化.圖8(b)顯示了HAEM相位參考項δρ?的圖,可以發現p1散射斑紋,即起源于空穴型α口袋和電子型ε口袋之間散射,基本為正值.進一步對包裹p1散射斑紋的圓圈內區域信號進行積分,如圖8(c)所示,實驗數據與理論計算在s±模型下得到的結果定性一致,因此判定該材料中存在能隙符號相反.結合細致的QPI分析得到具體的能隙數值,在圖8(d)中他們給出了考慮到能隙正負號后空穴型α口袋和電子型ε口袋的能隙隨角度的變化關系. 圖8 FeSe單晶的QPI測量和能隙相反的實驗證據 (a)FeSe單晶發生結構轉變后的費米面示意圖;(b)單雜質QPI數據得到的HAEM方法的相位參考量δρ?(qE=1.05 meV);(c)對電子-空穴口袋之間散射,即圖(a),(b)中的p1散射斑紋進行積分,得到的實驗結果和理論計算比較,結果和s±配對理論曲線定性相符合;(d)最終得到的兩個費米口袋上能隙隨角度的依賴關系[30]Fig.8.QPI experimental results and resultant gap function obtained in FeSe single crystal:(a)Schematic plot of Fermi surfaces below the structural transition temperature in FeSe;(b)calculated phase-referenced term δρ?(qE=1.05 meV)from the QPI data measured around a single non-magnetic impurity by HAEM’s method;(c)comparison between the experimental data and theoretical calculation results of δρ?(E)for the inter-pocket scattering spot p1between hole-like α and electron-like ε pockets,which conf i rms the s± pairing in FeSe;(d)angle dependence of superconducting gaps along the two Fermi pockets[30]. 在3.1節曾經提到,對于一些FeSe基的超導體,如FeSe單層膜、Li1?xFexOHFeSe等材料,因為在Γ點附近的空穴費米口袋沉到了費米能以下,僅在M點附近留下電子型費米口袋,費米面結構如圖1(b)所示.但是,對于s±配對模型,能隙變號發生在空穴型費米口袋和電子型費米口袋之間,而空穴費米面的缺失,似乎動搖了基于上述費米面結構提出的s±配對模型的基礎.然而,如果反鐵磁漲落仍然是這類FeSe基超導體電子配對的媒介,那么超導序參量必須存在反號,因此需要進一步的實驗來統一有和沒有空穴費米面存在的鐵基超導體的能隙形式. 圖9(a)和圖9(b)分別顯示了在FeSe單層薄膜[37]和Li1?xFexOHFeSe單晶[46]上測量的隧道譜,可以發現這兩個譜形極為相似:零能附近“U”形隧道譜表明體系沒有能隙節點,有兩對相干峰,對應著兩個超導能隙.但是早期的ARPES實驗發現[8?11],這兩種材料上只有一套電子型的費米面,那么兩個能隙如何存在于一套費米面是個令人困擾的問題.對于Li1?xFexOHFeSe材料,相干峰位置約為14.3 meV和8.6 meV.通過對隧道譜的擬合分析發現,這兩個能隙都需要是各向異性的,而能隙最大值對應著14.3 meV和8.6 meV. 圖9 FeSe單層薄膜[37]和Li1?xFexOHFeSe單晶[46]上測量的超導隧道譜Fig.9.Tunneling spectra measured on monolayer FeSe[37]and Li1?xFexOHFeSe single crystal[46]. 圖10 Li1?xFexOHFeSe的QPI測量和費米面及能隙結構 (a)14.5 meV的FT-QPI圖案;(b)費米面示意圖;(c)圖(b)中費米面的自關聯模擬;(d),(e)小能隙和大能隙的最大值處測量的FT-QPI圖案中心斑紋;(f)雜化后兩個電子口袋的軌道成分以及能隙分布[46]Fig.10.QPI results and Fermi surface of Li1?xFexOHFeSe:(a)FT-QPI pattern at 14.5 meV;(b)schematic plot of Fermi surface;(c)self-correlation of the Fermi surface shown in(b);(d),(e)FT-QPI pattern for the central spot measured at 8.6 and 14.5 meV;(f)orbital contents and gap maxima along the two electron pockets with hybridization[46]. 進一步用STM對Li1?xFexOHFeSe材料進行QPI測量,FT-QPI圖案如圖10(a)所示.圖10(c)是對圖10(b)的費米面示意圖進行自關聯來模擬FT-QPI圖案,與圖10(a)非常相似,證明了該材料中空穴費米面的確缺失了.通過細致的不同能量下的中心斑紋的QPI測量[46],可以發現雜化形成的內外兩套費米口袋,與后來的精細的ARPES結果發現的兩套嵌套的電子型費米口袋的結果[47]較為一致.進一步在不同能量下的測量發現內套散射環隨著能量升高先出現,在小能隙最大值8.6 meV附近,如圖10(d)所示,外套散射環開始出現,在大能隙14.3 meV處,內外環都顯示出來.通過分析認為,小能隙對應內套的電子型費米口袋(dxz/yz軌道成分為主),而大能隙對應著外套電子型費米口袋(dxy軌道成分為主),示意圖見圖10(f).雖然分辨出了雜化形成的內外兩套費米面,分別與小大兩個能隙相對應[46],但是對于這兩個能隙符號相反,還需要其他方法確定. 圖11 Li1?xFexOHFe1?yZnySe超導能隙符號的HAEM相位參考方法的甄別 (a)雜質點零場和11 T磁場下的隧道譜,插圖是該啞鈴狀雜質的形貌;(b)圖(a)插圖所示區域的QPI測量結果,即微分電導圖ρ(r,E=+8.5 meV);(c)圖(b)傅里葉變換后的FT-QPI圖案;(d)相位參考量δρ?(q,E=+8.5 meV)的結果,圖中的兩個圓圈之間的區域包含兩電子口袋間的主要散射,是δρ?(q,E)的積分區域;(e)δρ?(E)的積分實驗曲線,插圖是s±配對態和s++配對態的理論計算結果[31]Fig.11.Determination of the sign-reversal order parameter in Li1?xFexOHFe1?yZnySe by HAEM’s phase-referenced QPI method:(a)Tunneling spectra measured at the impurity site under a magnetic f i eld of 0 T and 11 T,respectively;(b),(c)QPI image ρ(r,E=+8.5 meV)and FT-QPI pattern ρ(q,E=+8.5 meV)measured at the area as shown in the inset of(a);(d)the phase-reference term δρ?(q,E=+8.5 meV)and the region within the two circles contains most of the signals from inter-and intra-pocket scatterings which is used as the integrated region of δρ?(q,E);(e)the experimental result of integral δρ?(E),and the inset shows the theoretical calculation results of integral signal for s± and s++pairing[31]. Zn雜質通常為非磁性的雜質,人為地在Li1?xFexOHFeSe中引入了少量的Zn雜質,可能占據在FeSe層的Fe位.雖然摻雜后Tc有所下降,但是在遠離雜質點位置測量的超導隧道譜與無摻雜樣品上測量的結果類似.圖11(a)的插圖顯示了Zn摻雜樣品中孤立的雜質周圍的表面形貌,在這里為了進行相位參考的QPI操作,雜質被嚴格移動到了視圖中心.通過隧道譜的測量,如圖11(a)所示,該雜質點在零場下的隧道譜表現出很尖銳的能隙內束縛態,而11 T的外加磁場僅僅壓制了雜質態的峰高和延展了雜質態的峰寬,并沒有移動雜質態峰的能量[31].如果該雜質是磁性的,磁場會與其自旋作用發生明顯的塞曼效應[24],對雜質態的能量造成移動,簡單計算1/2自旋在11 T磁場下大概移動0.64 meV,如果有該能量大小的移動是完全可以被STM分辨出來的.而磁場下的雜質態峰位置沒有移動,證明該雜質是非磁性的.根據前面3.2節的討論,如果非磁性雜質能夠在超導能隙內誘導出雜質態,這本身就說明了該材料具有反號的超導序參量[24].進一步的實驗證明應用3.4節提到的HAEM相位參考方法進行測量,圖11(b)和圖11(c)分別給出典型的QPI圖像ρ(r,E =8.5 meV)和FT-QPI圖案|ρ(q,E=8.5 meV)|, 其中FT-QPI圖案和圖10(a)所示的未摻雜樣品上測量的結果類似,證明摻雜并沒有明顯改變費米面結構,空穴型費米面仍然缺失.應用HAEM相位參考方法的(5)式,可以計算出δρ?(q,E=8.5 meV),如圖11(d)所示.其中兩個圓圈中間區域包含了兩電子口袋的大部分散射通道強度,而這部分信號大部分是正的,且有較大數值.積分兩個圈之間的信號得到的δρ?(E)繪于圖11(e)中,可以看出,實驗結果的曲線和基于s±配對的理論計算基本相符,和基于s++配對的理論計算結果有很大的區別.因此,上述結果表明在Li1?xFexOHFeSe系統中,兩個電子型費米口袋間能隙符號出現反轉.因為證明了該雜質是無磁性雜質,對于無磁性雜質,s++配對模式是不會出現能隙內的雜質態,因此該結果可以排除s++能隙.此外,從隧道譜上在零能附近看見的是“U”形的,因此可以排除節點型d波.對于無節點的d-波(nodeless d-wave)的情況,也不能得到解釋,因為所測量的結果是費米口袋內的小動量轉移散射行為,從而對于每一個費米口袋,能隙符號都是一致的,所以也可以排除無節點d波.從而確認了該材料的s±配對機理. 圖12 Li1?xFexOHFe1?yZnySe超導能隙符號的DBS相位參考方法的甄別 (a)基于插圖費米面結構不同配對對稱性下計算出來的隧道譜;(b)理論計算出來的相位參考量gpr(q,±E)在q空間的積分結果;(c)實驗測量的某個雜質附近和遠離雜質的隧道譜;(d)實驗測量并積分出的相位參考量gpr(±E)隨能量的變化[48]Fig.12.Determination of the sign-reversal order parameter in Li1?xFexOHFe1?yZnySe by DBS phase-referenced QPI method:(a)Calculated tunneling spectra at the impurity site and some impurity-free place in superconductors with dif f erent gap symmetries;(b)energy dependent integral signal of phase-referenced term gpr(q,±E);(c)tunneling spectra measured at the impurity site and some impurity-free place in Li1?xFexOHFe1?yZnySe;(d)integral signal of the measured phase-referenced term gpr(q,±E)[48]. 另一種相位參考的DBS-QPI方法同樣在Li1?xFexOHFe1?yZnySe材料中適用,基于僅有內外電子口袋的計算結果(如圖12(a)和圖12(b)所示[48])可以看出,計算結果定性地與既有電子又有空穴口袋的LiFeAs材料中的結果(圖6(b))一致.而實驗測量的隧道譜中(如圖12(c)所示),雜質態峰在正能非常強,負能相對較弱,不隨磁場移動的雜質態峰證明該雜質同樣為非磁性雜質.實際測量并積分得到的gpr(±E)結果如圖12(d)所示,可以發現,在負雜質態峰能量處,積分信號出現了一個負的峰,和s±配對非磁性雜質的理論計算定性一致.同時這一實驗在不同類型的非磁性雜質和多雜質的情況下也得到了相同的結論,證明該材料中能隙符號的確發生了變化[48]. 結合中子散射在Li1?xFexOHFeSe材料中的數據,可以進一步討論并確定該材料中兩個符號相反的能隙如何具體對應到兩套雜化形成的內外兩套電子型費米口袋上[49],這里不再贅述.在Li1?xFexOHFe1?yZnySe材料中的結果,證明了只有電子型費米面的鐵基超導材料中也存在著能隙符號的變化,說明了排斥勢導致的配對相互作用(很有可能是交換反鐵磁漲落)是鐵基超導體配對的主要原因.最近,在具有相同電子結構的FeSe單層膜中,利用STM研究發現了隧道譜上的玻色模,因此配對機理傾向于磁激發的機理[50],另外輸運研究中發現的線性磁阻行為也給出了自旋漲落的可能性[51].上述工作為統一重度電子摻雜中配對對稱性的起源提供了重要的實驗參考. 對于鐵砷基超導體的母體,在高溫時其晶格結構是四方相,隨著溫度的降低,晶格將會發生從C4到C2的對稱性轉變,變成正交相.當溫度略低于結構相變溫度,系統發生反鐵磁相變.雖然結構相變會影響電子態密度分布的各向異性,但是在母體中測量得到的二度對稱的電子激發行為無法用正交相的晶格結構所完全解釋,這樣二度對稱的電子相被稱為電子向列相(nematic electronic structure).最早電子向列相由STM在接近母體的摻雜CaFe1.94Co0.06As2材料上發現[52],在15 meV測量的特征電子結構如圖13(a)所示,電子態在橫軸方向有些拉長的長條.對實空間電子態做自關聯,得到的圖像會出現長度為8倍于Fe-Fe原子間距aFe-Fe的斑紋[52].圖13(b)顯示的是與圖13(a)對應的FT-QPI圖案,可以發現,FT-PQI圖案也表現出明顯的二度對稱性,三個豎條狀斑紋在q空間的距離也和實空間8aFe-Fe對應.這是鐵基超導母體電子向列相的實驗證據,而且與表面重構無關.之后,在LaOFeAs等[53],NaFeAs[54]材料中也相繼發現了類似的二重對稱性的電子態行為,如圖13(c)—(f)所示,而且這些二度對稱的電子態隨著能量的變化還有一定的色散關系.上述這些不同體系內進行的STM實驗證明了鐵基超導母體中的電子向列相的普遍性.開始是微觀觀測發現電子向列相,后來由各向異性的電阻測量[55,56]等實驗進一步證實,并且發現在母體中電子向列相的溫度甚至高于結構相變的溫度[57],出現所謂向列相的漲落.電子向列相的起源還有一定的爭議,有包括結構相變、反鐵磁漲落、軌道漲落這三個可能的原因[58].這一奇異的電子態和超導有一定的關系,并且豐富了鐵基超導體的電子態相圖. 圖13 鐵砷基超導母體CaFe1.94Co0.06As2樣品[52],LaOFeAs樣品[53]和NaFeAs樣品[54]中測量得到的QPI圖像和相應的FT-QPI圖案Fig.13.QPI images and FT-QPI patterns for the parent compounds of FeAs-based superconductors Ca Fe1.94Co0.06As2[52],LaOFeAs[53]and NaFeAs[54]. 如前所述,FeSe單晶結構簡單,且隨著溫度的降低只發生結構相變而沒有反鐵磁相變,當溫度低于結構相變后,體系的電子空穴費米口袋將會有很強的二度性.如前所述,該二度性甚至會影響到超導能隙的各向異性[30].在此情況下,研究FeSe材料中的電子向列相行為將是一個比較重要的問題.前面在鐵基母體材料中所得到的電子向列相是從FT-QPI實驗中發現的,而FeSe材料中測量的FTQPI圖案也有很明顯的二度對稱性,如圖14(a)和圖14(b)所示,而且隨著能量從正能到負能的改變,強度分布好像旋轉了90?.最近的研究表明,上述二度對稱的FT-QPI圖像,主要來源于FeSe中嚴重拉長的電子/空穴費米口袋結構[59].因為FT-QPI圖案是q空間的信息,FeSe電子或者空穴口袋袋內散射,都會集中在中心斑紋處.測量得到的中心斑紋,由不同費米面的色散關系,在正能測量時電子口袋內的散射的確應該占主要部分,而在負能測量時空穴口袋內的散射應該占主要部分.另外結合yz軌道比xy和xz軌道有著更大的態密度權重,可以基于費米面的結構解釋上述二度對稱的FT-QPI圖案,而不需要額外的電子向列相[59].因此,二度對稱的FT-QPI圖案并非主要來源于電子的向列相,而是主要來自于二度對稱的費米口袋.而電子態的各向異性在FeSe厚膜中卻有所體現,包括圖14(c)中顯示的由Se雜質產生的間距為16aFe-Fe的電子態的周期結構和圖14(d)中顯示拉長的磁通圖像.雖然后者可能是由各向異性的能隙造成的,與圖8(d)所示二度性的能隙對應,但是其拉長的方向和晶格方向相同,也驗證了電子態存在著各向異性.需要注意的是,FeSe單晶中不存在長程磁有序,低溫下形成的正交電子向列相會直接影響超導相,因此對FeSe超導電性的研究有著重要的意義. 圖14 FeSe中可能的電子向列相 (a),(b)不同能量測量的FeSe單晶的FT-QPI圖案[59];(c),(d)FeSe厚膜上Se雜質附近實空間的電子波調制和磁通圖像[39]Fig.14.Possible nematicity in FeSe:(a),(b)FT-QPI patterns obtained at dif f erent energies[59];(c),(d)possible nematic electronic nanostructure near a Se adatom and elongated vortex image in FeSe thick f i lm[39]. 對于普通超導材料,能帶在零能附近打開一個超導能隙?,通常材料能帶的費米能EF(eV量級)比超導能隙(meV量級)大得多.鐵基超導體是一個典型的多帶多能隙超導體,部分或者全部能帶的費米能EF非常小(幾十或者上百meV),在此情況下,超導能隙(幾個到十幾個meV)和費米能的比值?/EF較普通BCS超導體的來說大很多.淺能帶現象在FeSe和Fe(Se1?xTex)材料中更明顯.STM實驗中,可以通過測量不同能量的FT-QPI圖案得到能帶色散的信息,雖然無法得到各能帶在動量空間的具體位置,但能得到能帶的電子空穴屬性和費米能的大小.圖15(a)和圖15(b)顯示了FeSe單晶在12 T高場下測量的不同能量的FT-QPI強度組合得到的能量色散結果[40].因為該材料的費米能非常小,所以需要高場破壞超導能隙來得到清晰的能帶信息.這樣的結果和ARPES測量的能帶色散圖看上去類似,但是其中橫軸的量是q,不代表能帶在動量空間k的具體位置.圖15(a)給出的是空穴型能帶色散,其費米能(價帶頂的能量)大概在10 meV;圖15(b)給出的是電子型能帶色散,其費米能(導帶底的能量)大概只有3 meV.對比到該材料中2.5—3.5 meV的超導能隙可以發現,FeSe確實是一個能帶特別淺的材料. 當費米能非常小時,材料可能更容易滿足量子極限(T/Tc? ?/EF),那么就有可能觀測到1964年理論預測的能量分立的磁通束縛態(Carolide Gennes-Matricon state,CdGM state)[60,61].在0.48 K溫度和較高的4 T磁場下,使用STM針尖在FeSe0.45Te0.55磁通中心觀測到了CdGM態中的三個束縛態能級[62],如圖15(c)和圖15(d)所示.這三個峰對應的能量大約是0.45,1.20和1.90 meV,其比值是1:2.7:4.2,與理論上預言的CdGM態的一級,二級和三級能量比值很接近.此外,這些峰能量基本不隨測量位置的變化而變化,進一步驗證了它們是分立的磁通束縛態.考慮到CdGM能級能量Eμ= ±μ?2/EF(μ =1/2,3/2,5/2,···),以及超導能隙范圍在1.1—2.1 meV,能夠計算出費米能的范圍約為1.3—4.9 meV,和角分辨光電子譜得到的結果類似[63],進一步驗證了材料的淺帶效應. 可以發現,FeSe和Fe(Se1?xTex)材料中,超導能隙和費米能的比值大概為1/5 圖15 FeSe基材料中的淺能帶行為 (a),(b)由高場12 T下FeSe單晶的FT-QPI推得的能帶色散關系圖[40];(c),(d)磁場4 T下測量的FeSe0.45Te0.55單晶磁通中心的磁通束縛態[62]Fig.15.Shallow band properties in FeSe-based superconductors:(a),(b)Band dispersions deduced from the FT-QPI pattern in FeSe measured at high magnetic f i eld of 12 T[40];(c),(d)vortex bound state peaks observed at the vortex core center in FeSe0.45Te0.55at a magnetic f i eld as high as 4 T[62]. 拓撲超導是凝聚態物理中的前沿領域之一.理論預測拓撲超導具有奇宇稱超導序參量,可能出現Majorana費米子,并在量子計算中有潛在應用前景[66,67],這使其備受關注.在拓撲超導中,磁通中心將會出現理論預言的Majorana零能模[66,67].因為拓撲超導很難尋找,通常用超導鄰近效應來誘導,如在s波超導體上生長拓撲絕緣體薄膜誘導出超導來嘗試實現,而磁通芯子中的Majorana零能模就首先在Bi2Te3/NbSe2異質結上被觀測到[68].最近,在摻雜的拓撲絕緣體材料CuxBi2Se3中也觀測到了可能的Majorana零能模峰[69].在拓撲半金屬Cd3As2表面,使用針尖誘導的超導中,也觀測到了可能的Majorana零壓電導峰[70].在鐵基超導體FeSe單層薄膜上,利用分子束外延生長技術沉積Fe原子,在Fe原子上也觀測到了可能的零能模,這一零能模對應的超導Tc更高,而且不需要外加磁場誘導[71]. 同時,鐵基超導體本身與拓撲的關聯也已“悄然”建立.在FeSe1?xTex材料中,由于布里淵區Γ點附近的pz和dxz/dyz軌道間的強自旋軌道耦合并導致能帶反轉,被理論預言[72,73]具有可能的拓撲表面態,而且利用自旋分辯的ARPES發現在該材料中存在自旋螺旋型的Dirac表面態[74].進一步的STM實驗在小磁場下在該材料磁通中發現了可能的Majorana零能模[75].圖16(a)是在0.5 T較小磁場和0.55 K較低溫度下測量得到的FeSe0.45Te0.55的磁通芯子圖像,圖16(b)和圖16(c)是一系列過磁通中心測量的隧道譜.可看到在磁通中心點測量的隧道譜有著尖銳的零能峰,在空間延展而不劈裂也不移動.實驗中還在該磁場下發現第一級CdGM磁通束縛態峰,其能量大概在0.7 meV,和觀測到的零能峰可以區別開.作者認為該實驗結果表明磁通中心存在著Majorana零能模. 最近在另一個FeSe插層材料(LixFe1?x)OHFeSe厚膜中,也觀察到可能的Majorana零能模[76].利用ARPES在該材料的Γ點附近也發現了Dirac型線性色散的表面態和Dirac點.通過STM測量得到的磁通束縛態,在其中發現零能有個明顯的峰,且不隨空間位置的變化而劈裂或移動.除了零能模以外,在正負能各有幾個非零能的峰.作者認為它們分別來源于表面p波超導磁通束縛態(0級即為Majorana零能模)和體s波超導普通CdGM磁通束縛態[76]. 上述兩種鐵基超導材料磁通中發現的零能模是否是Majorana零能模,以及是否就說明出現了拓撲超導,還需要進一步的實驗驗證.如果證實,那么鐵基超導體可能是一個“天然”的拓撲超導體,這為操縱Majorana費米子并最終實現容錯量子計算提供了一個新的平臺. 圖16 FeSe0.45Te0.55磁通芯子中觀測到的Majorana零能模[75]Fig.16.Majorana zero-energy mode observed in the vortex core in FeSe0.45Te0.55[75] 近十年來,關于鐵基超導體的STM研究取得了一系列重要進展,本文在鐵基超導機理和其中的奇異電子態方面進行了簡要總結.但是需要注意的是,鐵基超導體是一個多帶多能隙系統,不同材料的費米面有很大的區別,另外還有各種有序態相互競爭或合作,呈現出紛繁復雜的物理現象.目前得到基本一致的認識是超導與反鐵磁漲落密切相關,但是電子配對是強耦合情況下的局域配對還是弱耦合情況下的延時配對仍然沒有定論.鐵基超導體表現出來的淺能帶效應、多種有序相的競爭和合作,也許是理解其非常規超導機理的關鍵,而掃描隧道顯微鏡實驗將會發揮重要作用. 由于在鐵基超導體上進行掃描隧道顯微鏡研究的小組很多,結果也極其豐富,我們這篇短文不可能作全面概括.如果有優秀工作沒有被概括進來,敬請原諒.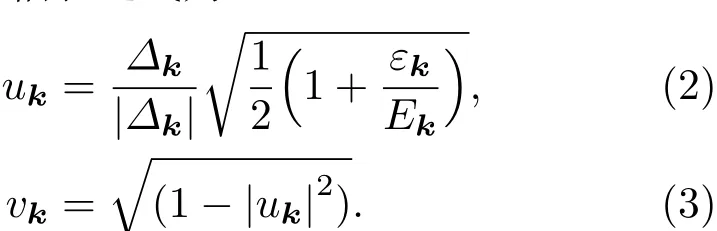
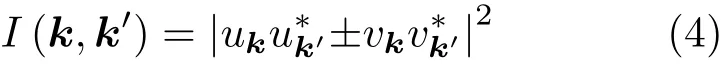
3 STM對鐵基超導體能隙的研究
3.1 鐵基超導體配對對稱性簡介
3.2 有空穴和電子費米面的鐵基超導體s±配對的STM證明

3.3 相位敏感的QPI技術及其理論分析
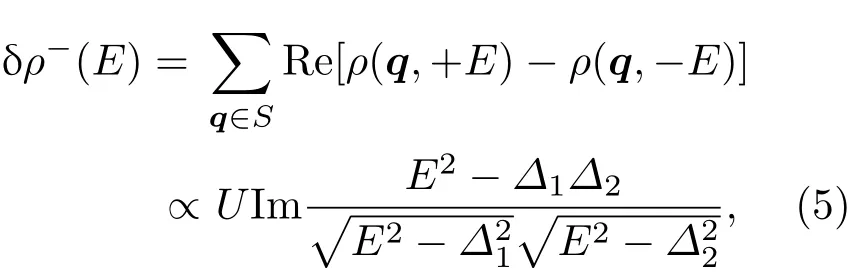
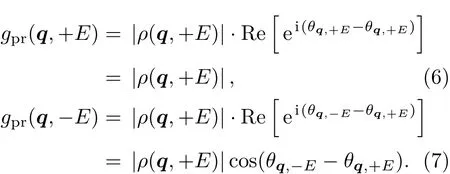

3.4 FeSe單晶超導體配對對稱性
3.5 空穴費米口袋缺失的FeSe基超導材料的配對對稱性研究

4 鐵基超導體中奇異電子態的STM研究
4.1 電子向列態
4.2 鐵基超導中的淺能帶效應
4.3 鐵基超導體中可能的Majorana零能模的發現
5 結論與展望

