上行鏈路大氣波前畸變對剪切光束成像技術的影響

蘭富洋 羅秀娟 樊學武 張羽 陳明徠 劉輝 賈輝

1)(中國科學院西安光學精密機械研究所,西安 710119)

2)(中國科學院大學,北京 100049)

剪切光束成像(sheared-beam imaging,SBI)技術是一種利用三束剪切相干激光照明的非傳統成像技術,該技術通過探測器陣列接收目標反射回波的散斑圖進行計算成像,在對遠距離暗弱目標高分辨率成像方面有著獨特的優勢.大氣湍流引起的光束波前畸變是影響SBI成像質量的一個關鍵因素,因此本文從湍流引起的激光波前畸變對目標頻譜信息提取的影響入手,建立了光束波前畸變對成像影響的理論模型.利用多層相位屏模型模擬了近地25 km大氣對SBI光束傳輸的影響.通過計算機仿真,得到了不同激光發射孔徑和不同成像距離時SBI的成像結果.仿真結果表明,選取合適的發射孔徑尺寸可以有效緩解湍流對光束波前質量的影響,從而提升成像質量.在Hutchin的研究基礎上,對孔徑選擇范圍的已有研究成果進行了擴展與深化.給出了SBI系統發射孔徑尺寸選取的建議,為SBI對不同高度目標成像的像質差異分析提供了參考.

1 引 言

大氣的湍流效應嚴重制約了地基光學成像系統的成像能力,為了實現對空間目標的高分辨率成像,需要同時突破光學系統口徑和大氣湍流影響這兩方面的限制.近幾十年來,在研究人員不斷增大望遠鏡口徑并結合自適應光學技術試圖解決這一問題的同時,采用激光主動照明的非傳統成像技術以其獨有的優勢[1]受到了人們的關注.剪切光束成像(sheared-beam imaging,SBI)技術[2,3]便是其中的一種.該技術不需要精密的光學成像器件,通過發射微小頻移的剪切光束和接收散斑拍頻信號進行計算成像,不僅能通過主動成像方式對空間暗弱目標進行觀測,而且繼承了激光干涉成像技術分辨率高的優勢.同時,其相位差測量方法能有效補償下行鏈路大氣湍流對成像的影響.隨著當前激光器技術的發展,SBI成為最具前景的遠程激光干涉成像技術之一.目前,SBI還有很多技術和工程問題待解決,尚處于探索研究階段.

通過對SBI成像機理的研究,發現SBI成像質量與照射到目標面上光波的波前質量密切相關.在SBI成像過程中,光束波面受到大氣湍流相位起伏效應的影響而產生畸變,最終導致到達目標面上的波前質量下降,這將對目標信息的準確獲取產生不利影響.本文首先從成像原理入手,分析了上行鏈路大氣湍流引起的波前相位畸變對SBI成像性能的影響,然后通過計算機仿真研究了湍流環境下,激光發射孔徑尺寸和目標高度對成像結果的綜合影響,并給出了相應結論.

2 成像原理

SBI成像原理如圖1所示[4],三束具有微小頻差的激光從不同孔徑發射同時照射到目標上,發射孔徑以“L”形式分布,間距分別為sx,sy.每一束光的反射回波中都包含目標信息[5],最終三束光的反射回波在接收面上疊加干涉.對探測器陣列接收到的回波信號進行解調[6],即可得到目標的傅里葉頻譜信息,最后利用傅里葉逆變換重構目標圖像[7].

圖1 SBI成像原理示意圖[4]Fig.1.Schematic of SBI principle[4].

三束光在目標表面疊加的光場可表示為[8]

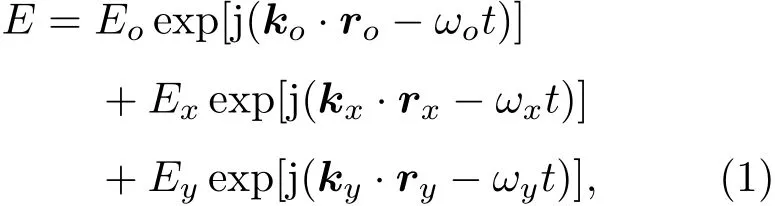
式中Eo和ωo為O光的振幅及角頻率;Ex,Ey和ωx,ωy分別為X光和Y光的振幅與角頻率;ki(i=o,x,y)分別為三束光的波矢;ri表示從發射孔到目標表面的位移矢量;t為時間.經目標反射后,反射回波到達接收平面時的光場為

則在探測器陣列平面上可以接收到隨時間變化的光強為

對光強信號I(x,y,t)進行解調,根據光束間的已知頻差可提取出?Φ1和?Φ2,此即為目標頻譜面上每一點與相鄰點間的相位差,其關系如圖2所示.根據頻譜面各點間相位差關系,通過多次循環迭代即可得到目標頻譜的相位分布.最后結合解調出的振幅信息還原完整的目標頻譜,通過傅里葉逆變換重構出目標圖像.

光束通過大氣傳播時其相位受到顯著影響而強度基本保持不變.SBI根據回波幅值與相位恢復目標信息成像的原理,決定了成像結果會受到光波相位畸變的影響.對于下行鏈路,每個探測器單元所接收到的反射回波均經歷了相同的大氣環境,回波散斑之間的相位差不變,因此下行鏈路大氣湍流并不影響反射回波間相位差的準確提取[9].而對于上行鏈路,每束光經歷了不同的大氣路徑,這給每束光所攜帶的目標信息引入了相位畸變,得到的目標頻譜相位也將與真實相位產生偏離,勢必導致重構圖像質量的下降,因此本文著重考慮上行鏈路大氣引起的波前畸變.這里采用目標圖像與重構圖像的Strehl比來衡量湍流對SBI成像質量的影響.Strehl比的定義為

圖2 相位復原方法示意圖Fig.2.Schematic of phase reconstruction method.

其值在0—1之間.對于目標圖像A(m,n)和重構圖像B(m,n),二者強度分布越相似,其Strehl比值越趨近于1[10],表明成像質量越好.

3 波前畸變影響分析

激光在湍流大氣中傳播時,受大氣折射率分布隨機起伏的影響,光束截面內不同部分所經歷的光程存在差異,最終導致光波前相位分布的隨機起伏.本節基于上行鏈路大氣湍流的影響,建立波前畸變對目標頻譜影響的理論模型,為便于分析,將模型簡化,僅考慮湍流最終對目標面上波前造成的影響.

首先考慮大氣低階擾動的影響(圖3),即湍流僅導致SBI各路光束的波前隨機地整體提前、滯后或傾斜,這種低階擾動使不同光束間的波前相位差為常數,此時目標面上光場可表示為

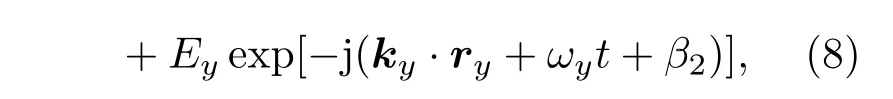
式中β1,β2代表后兩束光的波前相對于第一束光波前的活塞相位差[11](gross-piston phase dif f erence),根據(5)式可得最終接收到的光強信號為

圖3 大氣低階擾動對目標頻譜相位的影響 (a)理想目標頻譜相位;(b)大氣低階擾動引入的誤差相位;(c)實際得到的目標頻譜相位Fig.3.Inf l uence of low-order atmospheric turbulence on spectrum phase:(a)Distribution of target ideal spectrum phase;(b)distribution of phase error induced by low-order atmospheric turbulence;(c)actual target spectrum phase distribution with phase error.

其中?β12=β2?β1.這樣根據光束間的已知頻差從時序光強信號I(x,y,t)中提取到的相位不再是目標頻譜面上相鄰點間的相位差?Φ1和?Φ2,而是包含波前相位偏移的復合相位差?Φ1+β1和?Φ2+β2.此時所得頻譜相位分布為原始相位與所引入的誤差相位的疊加(圖3(c)),尺寸為N×N,誤差相位的分布如圖3(b)所示,其為一斜面,斜率由β1,β2決定.

若理想情況下目標頻譜相位為?(x,y),則受誤差相位影響后的目標頻譜相位表達式為?(x,y)+β1x+β2y,將該畸變相位代入目標重構公式可得

式中F?1{···}為傅里葉逆變換;根據傅里葉變換的相移定理[12],O′實際上是真實目標圖像在x,y方向上的平移,如圖4所示,偏移量分別由β1和β2決定.

圖4 大氣低階擾動對成像的影響 (a)目標圖像;(b)無湍流情況下單次成像結果;(c)大氣低階擾動下單次成像結果Fig.4.Inf l uence of low-order atmospheric turbulence on imaging:(a)Target image;(b)reconstructed image from a single shot without turbulence;(c)reconstructed image from a single shot with the inf l uence of low-order atmospheric turbulence.

由此可知,大氣低階擾動引起的光束波前相位整體偏移并不影響成像質量,僅使重構圖像中目標位置發生平移.由于SBI需要通過疊加平均多幅重構圖像來消除散斑效應[13],而這種相位隨機抖動使每幅重構圖像中目標的位置都不同,不可直接進行疊加.可利用圖像配準技術使每幅圖像中目標位置得以匹配,然后對疊加后的圖像周期延拓,裁取出完整目標.

對于大氣高階擾動的影響,當三束光經歷不同的湍流路徑到達目標面時,光束波前不同位置的相位受高階擾動影響產生隨機抖動,不同光束間的波前相位差不再是常數.此時接收面上的光場為

式中βi(i=o,x,y)為由不同路徑湍流引起的高階波前相位畸變分布.式中每一項頻譜的復振幅分量都引入了與βi(i=o,x,y)有關的隨機相移,這樣探測器陣列所接收到的頻譜是由存在不同程度誤差的復振幅分量疊加而成的,與真實目標頻譜存在偏差,且這種偏差會隨著波前相位畸變的加劇而變得更為嚴重.湍流引起的波前相位畸變程度用波前畸變均方根值(root meam square,RMS)[14]來衡量,對三種目標進行仿真,不同程度波前畸變對成像質量的影響如圖5所示.

圖5 目標面波前質量對成像的影響Fig.5.Dependence of image Strehl ratio on wavefront RMS.

從圖5可以看出,對于不同目標,當波前RMS小于λ/20時,隨著RMS的增大,重構圖像Strehl比值整體變化不明顯,僅在接近λ/20時出現輕微下降的趨勢,此時波前畸變引起的目標頻譜誤差較小,對成像質量無明顯影響;而當波前RMS大于λ/20時,重構圖像Strehl比值迅速下降,此時波前相位畸變引起的目標頻譜誤差較大,對成像影響顯著.

目標面上的光波前是由透過大氣后的波前在真空中衍射傳播形成的.因此,目標面上波前質量也是由透過大氣后光束波前質量和衍射傳播距離共同決定的.對于透過大氣后光束的波前質量,其除受大氣湍流強度影響外,還與激光發射孔徑尺寸有關,當發射孔徑尺寸在大氣相干長度之內時,光束波前主要受大氣低階擾動的影響;而當發射孔徑尺寸超出大氣相干長度后,光束波前受大氣高階擾動的影響顯著,且隨著孔徑尺寸的增大波前相位畸變程度加劇.然而,即使透過大氣后光束波前質量較差,經過遠距離的衍射傳播到達目標面時仍可能衍射出較好的波前[15].

綜上所述,目標面波前質量實際上是由湍流強度,發射孔徑尺寸和成像距離共同決定的.因此在實際應用中,除了將SBI系統建設在湍流較小的地區,還應根據成像距離選擇合適的激光發射孔徑,進一步緩解湍流對波前的影響,Hutchin在經典文獻[15]中指出,只要將SBI發射孔徑直徑控制在0.2—2.0倍的大氣相干長度r0內,經過衍射傳播后,光束中心區域就能夠形成近乎完美的波前.本文在Hutchin研究的基礎上,對不同軌道高度的目標進行成像仿真,以研究湍流環境下發射孔徑尺寸對不同高度目標成像質量的影響.

4 仿真研究

4.1 大氣湍流的多層相位屏模擬

大氣湍流主要發生在離地面垂直高度20 km以下,且隨著高度的增加而減弱.通常用大氣折射率結構常數評價湍流強度,若越小,則湍流越弱.本文大氣折射率結構常數采用經典的Hufnagel-Valley模型[16]

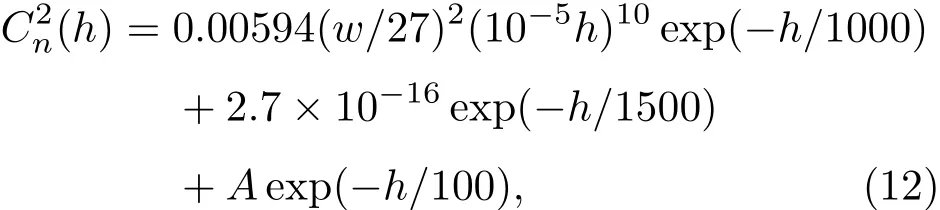
這里利用多層相位屏模擬垂直高度25 km內的大氣湍流,相位屏的個數和位置通過等Rytov指數間隔[17]的方法設置,Rytov指數的定義為[18]

式中?hi為第i層大氣的高度;(hi)為第i層大氣折射率結構常數的路徑平均值;k為波數.等Rytov指數是指選取合適的?hi使每一層Rytov指數(?hi)的值相等,通常(?hi)應小于0.1,且不超過全路徑上光強起伏的10%,即[19]

其中L為光束在大氣中的傳播距離.這里每層大氣的Rytov指數取為0.001,將大氣分為25層,每層高度分布如圖6所示,可見該方法不僅充分考慮了全路徑上不同高度的大氣區域,而且根據區域內湍流的強弱設置不同數目的相位屏以實現充分采樣.由Hufnagel-Valley模型和所模擬的大氣總高度決定的總的大氣相干長度r0為11.6 cm,屬于一般情況的大氣條件.選用Kolmogorov譜作為大氣湍流功率譜模型,通過快速傅里葉變換(fast Fourier transformation,FFT)譜反演法生成每一層的相位屏,光束在相位屏間按菲涅耳衍射進行傳播[20].

圖6 高度廓線與分層高度Fig.6.Phase screen heights with a plot ofprof i le overlayed.

4.2 仿真結果與分析

利用4.1節的湍流模型生成不同高度目標面上的波前,目標高度范圍為300—1000 km,目標尺寸2 m,激光波長1064 nm,SBI系統探測器陣列維數為80×80,根據本文模擬的r0=11.6 cm與Hutchin[15]給出的孔徑選擇范圍,發射孔徑直徑在3—23 cm選取.不同高度和發射孔徑尺寸下目標面上波前RMS如圖7所示,每組結果為50次仿真的均值.

從圖7可以看出,隨著發射孔徑的增大,對于不同高度的目標,目標面波前質量均存在下降趨勢.然而隨著軌道高度的增加,波前質量受孔徑尺寸影響程度逐漸減小.這是因為對于更高軌道的目標,光波透過大氣層后傳播了更遠的距離,此時到達目標面上的波前主要包含初始波前的低頻成分,更趨近于平面波,所以具有更好的波前質量.根據第3節中的結論,這里以波前RMS小于λ/20作為能夠高質量成像的條件.發現對于不同高度的目標,孔徑尺寸在r0以內時均能獲得RMS小于λ/20的波前.當軌道高度大于800 km,發射孔徑直徑在0.2r0—2r0內取值時其波前RMS均小于λ/20;而對于高度低于800 km的目標,目標面波前質量受發射孔徑影響較為明顯,發射孔徑直徑在2r0附近時波前RMS均大于λ/20,且高度越低,RMS值越大.下面分別給出目標高度為300 km和1000 km時,采用不同發射孔徑得到的成像結果,每張圖像均由30次重構圖像疊加平均得到.如圖8、圖9所示,圖片上的數字為Strehl比值.

圖7 不同發射孔徑和目標高度下目標面波前RMSFig.7.Wavefront RMS for dif f erent values of transmitting aperture diameter and target height.

圖8 300 km高度目標在不同發射孔徑下的成像結果及其Strehl比值Fig.8.Imaging results and Strehl ratio values for varying transmitting aperture diameter with target height of 300 km.

圖9 1000 km高度目標在不同孔徑下的成像結果及其Strehl比值Fig.9.Imaging results and Strehl ratio values for varying transmitting aperture diameter with target height of 1000 km.

可見對于300 km高度目標,發射孔徑直徑超過大氣相干長度后,成像質量明顯下降;發射孔徑直徑達到2r0時無法識別目標;而對于1000 km高度目標,其成像質量隨孔徑增大無明顯變化,均能重構出清晰的目標圖像.因此,在根據文獻[15]給出的范圍選擇孔徑尺寸時,還需充分考慮目標高度這一因素以保證成像質量.當發射孔徑直徑選在r0—2r0時,對于較低高度的目標,可能會獲得較差的成像質量甚至無法成像.

5 結 論

本文研究了上行鏈路大氣湍流導致的光束波前畸變對SBI質量的影響,對成像過程進行了理論建模分析,并在不同成像條件下進行了多組仿真實驗.

1)研究表明,大氣湍流引起的目標面波前畸變直接決定著SBI系統的成像能力.但在湍流強度一定時,通過合理選擇發射孔徑尺寸可以有效改善SBI成像質量.

2)仿真結果顯示,從波前質量的角度來看,為保證成像質量,發射孔徑尺寸選取的上限受目標高度的制約.因此,在以Hutchin給出的范圍為指導的前提下,還需結合不同高度成像需求確定孔徑尺寸上限,確保將目標面波前RMS控制在λ/20內.而從能量角度來看,較小的孔徑尺寸會導致更嚴重的光束發散,降低到達目標面的光束能量,不利于回波信號的接收與信噪比的提升,或對成像帶來不利影響,這對發射孔徑尺寸的下限提出了要求.因此在SBI系統孔徑的實際選擇中,應從波前質量、能量等多方面入手,進一步縮小取值范圍,尋求最優孔徑尺寸.

3)本文為SBI系統發射孔徑尺寸的選取提供了理論指導和參考,為SBI對不同高度目標成像時潛在的像質差異提供了新的分析思路.