數學文化:高考怎么考,考生怎么答
史嘉
2016年9月,教育部考試中心下發《關于2017年普通高考考試大綱修訂內容的通知》,公布了2017年普通高考各科考試大綱修訂內容,數學學科與前兩年悄悄地考查數學文化不同的是,這次高調通知“在能力要求內涵方面……增加了數學文化的要求”.果真,數學文化內容的考查在2017年的課標I、Ⅱ卷中均有體現,今后的高考試卷中也會成為常客.
可見,高考“考查”數學文化將是常態.但是可以命制高考試題的數學文化素材(如數學古籍、數學史料等)浩如煙海,同學們普遍感到備考束手無策.考生們又該如何備考、答題呢?我們先梳理近三年課標卷中的數學文化試題,看看高考是怎么考的,
一、數學文化高考試題
什么是數學文化高考試題,沒有明確的權威的概念界定,這里主要列舉以數學史料為背景的考題.
從以上統計看,課標卷已經將考查數學文化作為“規定動作”,且均以選擇題形式考查中國古代數學取得的成就.
二、對比欣賞數學文化高考試題
我們來一起看看這類試題具體是以怎樣的角度和形式考查的,對我們解答此類試題又有怎樣的影響.
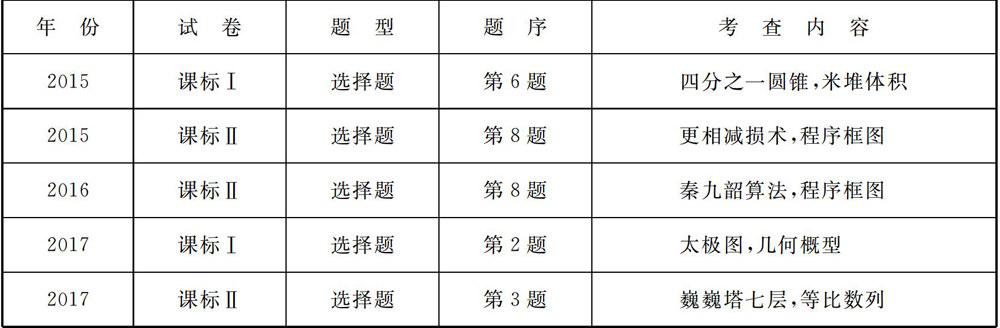
試題1 (2015年課標工卷第6題)《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有委米依垣內角,下周八尺,高五尺.問:積及為米幾何?”其意思為:“在屋內墻角處堆放米(如圖1,米堆為一個圓錐的四分之一),米堆底部的弧度為8尺,米堆的高為5尺,問米堆的體積和堆放的米各為多少?”已知1斛米的體積約為1.62立方尺,圓周率約為3,估算出堆放斛的米約有()
A. 14斛
B.22斛
C.36斛
D. 66斛
仔細審題,發現該題就是在米堆和古代度量單位的背景下考查計算四分之一圓錐(給出弧長和高)的體積(或者說容積).從思維量和計算量看應該屬于簡單題.
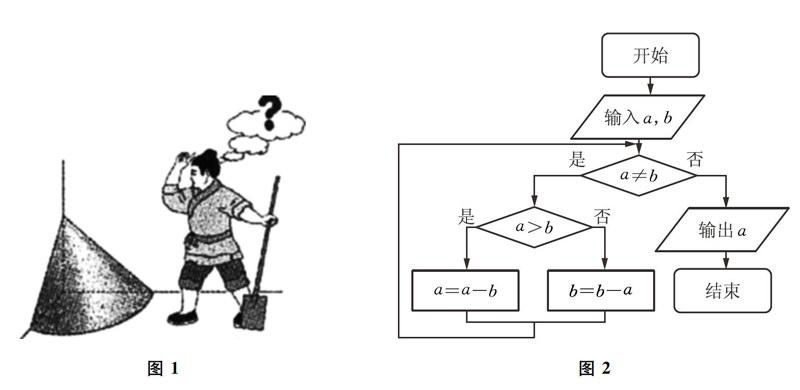
試題2 (2015年課標Ⅱ卷第8題)如圖2所示的程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”.執行該程序框圖,若輸入a,b分別為14,18,則輸出的a=()
A.0
B.2
C.4
D. 14
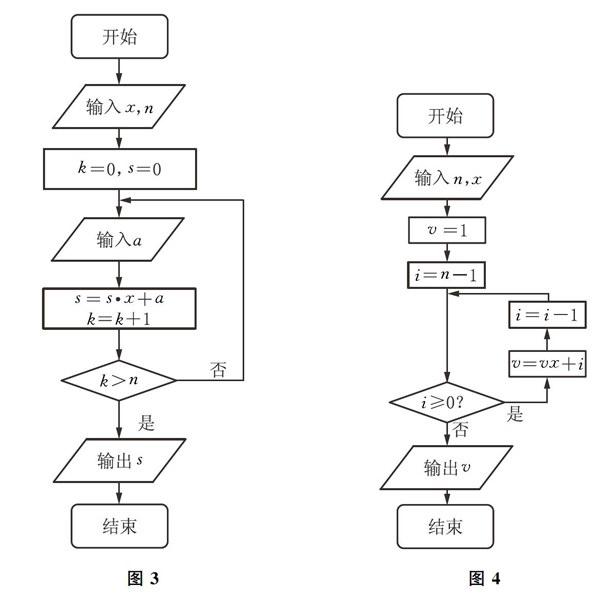
試題3 (2016年課標Ⅱ卷第8題)中國古代有計算多項式值的秦九韶算法,圖3是實現該算法的程序框圖.執行該程序框圖,若輸入的x=2.n=2,依次輸入的a為2,2,5,則輸出的s=()
A.7
B.12
C.1,
D. 34
兩道題均取材于中國古代數學著名算法——更相減損術和秦九韶算法,而且都直接改編自教材——人教A版第一章《算法初步》第1.3節《算法案例》.2016年四川卷第6題也是考查秦九韶算法.
試題4 (2016年四川卷第6題)秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法,如圖4所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例.若輸入n,x的值分別為3,2.則輸出v的值為( )
A.9
B.18
C.20
D. 35
通過對以上四道數學文化試題的對比分析,我們發現了解有關數學文化背景,可以領略古代算法思想的力量,理解問題及其算法的意義,擺脫機械解題訓練造成的無意義學習與思想麻木,
三、關于備考數學文化試題的一點建議
以《九章算術》為代表的中國古代數學具有“寓理于算”的特征,這不同于以《幾何原本》為代表的古希臘數學(他們注重邏輯的演繹).我國古代數學成績輝煌,數學古籍有《周髀算經》《九章算術》等“算經十書”;宋元時期涌現出一批著名的數學家,如賈憲、秦九韶、楊輝、朱世杰等等,他們的數學成就在很多領域都達到了中國古代數學、甚至是當時世界數學的巔峰.
鑒于中國古代數學的特征,數學文化高考試題多集中在考查幾何體、數列和算法等知識模塊,如把古籍中的幾何體(陽馬、鱉膈、牟合方蓋等)或古代器皿、測量工具(樽、天池盆)與三視圖相結合,與數列相結合的古代名題(《九章算術》中此類問題較多,如竹九節等;2017年課標Ⅱ《算法統宗》“巍巍塔七層”等),更多的則是把著名的算法以框圖形式考查,既回避古語原文,變晦澀為明了,抽象為直觀,完全符合高考試卷的要求.
因此,以數學史、數學名著為背景的數學文化考題大多屬于中檔試題,要注重閱讀理解試題的文字敘述與數學內涵,而不要被其外衣嚇倒,可以發現試題考查的都是數學史上重要的或常規的知識、方法和思想.而這些,正是數學文化的要義所在.

