基于BC1群體的多性狀QTL定位方法

佟 良 胡家晶 張小藝 孫 威

（綏化學院信息工程學院 黑龍江綏化 152061）

過去有很多科學工作者利用遺傳標記的基本原理研究QTL，其中Jansen 1993給出了多個數量性狀的區間作圖方法[1]。Kaoet al.1999在CIM的基礎上，發展形成一種新的作圖方法——多區間定位方法MIM[2]，該方法可同時對多個區間進行多個QTL作圖，已被證明是比CIM更準確的估計方法。

之后，許多科學工作者在前人的基礎上進一步推廣，提出了一些適合特定情況的QTL分析方法，在其相應的范圍內也有其作用。如考慮基因多效性和 (Q×E)交互，Jiang和Zeng 1995基于極大似然思想提出了多性狀復合區間定位方法MT-CIM[3]。方法可同時對多個性狀進行復合區間作圖，相對于MIM能更好的提高QTL定位參數估計的精度。還有.Knott S A et al應用回歸分析思想對多性狀基因位點進行定位分析[4,5]。Xu et al 2005基于表型性狀為多個離散的二進制對QTL進行了聯合定位[6]。Guoet al 2007基于表型性狀為不完整的數據對多性狀QTL進行了定位研究[7]。Liu 2007與Banerjee et al.2008基于貝葉斯方法對多性狀基因進行了研究[8,9]。Zeng 2012基于MIM思想，應用MT-CIM的模型提出了多性狀多區間定位方法MT-MIM[10]。通過分析，MT-MIM方法的準確性高于MIM方法和MT-CIM方法。

多性狀QTL定位方法，相對于單一性狀QTL定位方法提高了檢測功效、定位的精確度和估計功效。這是因為在多個表型性狀條件下，單一性狀QTL定位方法完全忽略了一個QTL對多個表型性狀的共同影響。多性狀QTL定位是關于多性狀的一個QTL多效性檢驗，如果性狀間存在較強的遺傳相關，通過多性狀QTL定位探測的功效是最高的[11].這些優勢在動物[12,13]和植物[14]研究中得到廣泛應用。

本文是在MT-MIM方法的基礎上進一步拓展，給出了每個QTL基因型的重組率顯性表達式，通過模擬對比MT-MIM方法，新方法對加性效應，顯性效應的估計比MT-MIM方法要好。新方法通過重組率定位QTL在染色體上的位置明顯好于MT-MIM方法。

一、背景知識與方法

（一）記號與背景。假定個雜交個體，個標記位點緊密連鎖構成個標記區間，為表型性狀個數。令,Yjt（j=1,…,n,i=1,…，t）表示第j個個體第i個表型性狀值，X*jt（j=1,…,n,i=1,…，q+1）表示第j個個體第i個標記區間內的QTL基因型，Xji（j=1…,n,i=1,…,q+1）表示第j個個體第i個標記的標記基因型。我們對QTL基因型數字化

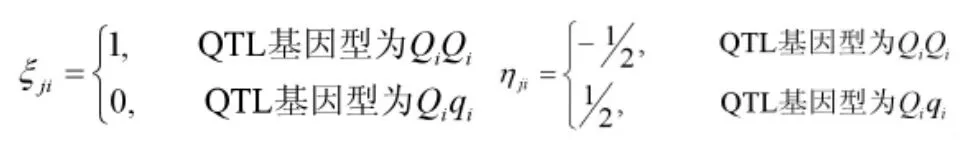
令ri和ri1分別表示第i個標記區間兩側標記之間的重組率和第i個標記區間內QTL與上標記位點之間的重組率。假設BC1群體每一個標記區間至多有一個QTL，第j個個體第個i標記區間已知時，其標記區間內QTL條件概率見表1

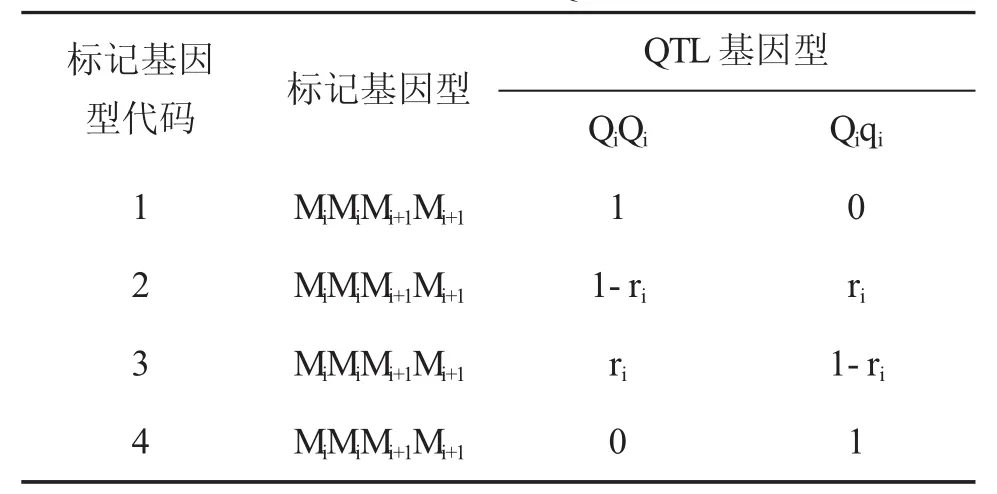
表1 標記基因型已知情況下QTL基因型的條件概率

（二）模型與似然函數。本文應用的統計模型是基于MIM思想，在MT-CIM模型的基礎上提出的統計模型[15]

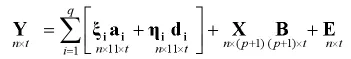
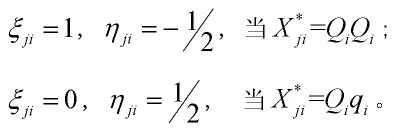
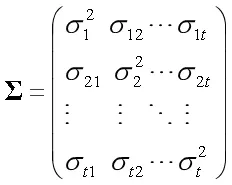
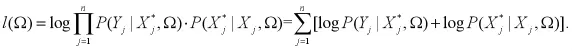
（三）EM算法。對于E步，考慮X，Y,Ω(S)我們計算l（Ω）的條件期望

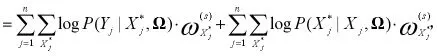
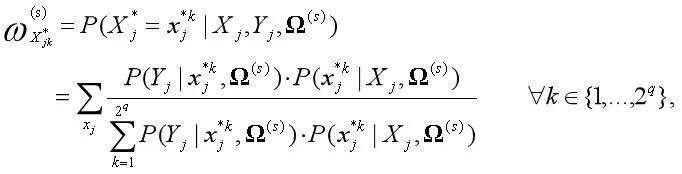
（四）參數估計。

1.C和Σ的估計。通過推導得出如下加性效應和顯性效應的迭代表達式[15]

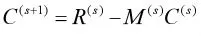
這里的 R(S)和 M(S）的表達式為

上式是R(S)對Joehanes[15]文章的修定，（Y-XB(S)）'W(S)Di修定為D'iW'(S)（Y-XB(S)）,i=1,...，cq。W=[ωx*jt]是一個n×2q的矩陣分別為第 i個 QTL第 k個表型性狀加性效應和顯性效應，D=（D1,D2,D3,…，Dcq），這里c的取值為1或者2。當只考慮加性效應時c=1，既考慮加性效應又考慮顯性效應時c=2。當c=2時

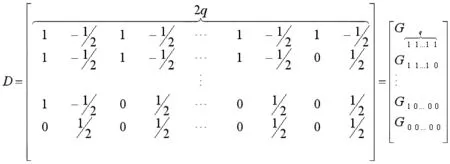
2.γ的估計。假定標記區間及其區間內的QTL具有關系表達式[16]，

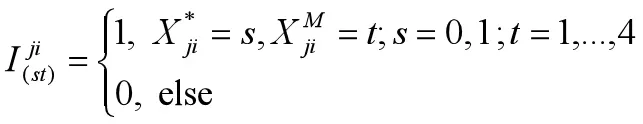
這里的j=1,...,n,i=1,...q.通過上面的示性函數可把Q函數第二部分和變形為如下形式

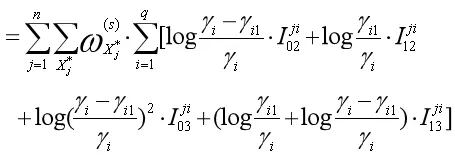
對上式進行極大化，可得重組率的顯性表達式

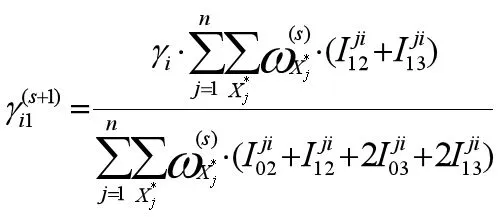
二、模擬與結果

為了評估給定參數估計方法的好壞，將本文提出的方法MT-MIM-BC1與MT-MIM進行對比。在不失一般性的情況下，模型中只考慮兩個數量性狀，2個QTL位點。由于估計的準確性隨著標記區間的減小，逐漸提高，標記區間長度取定10cM。MT-MIM-BC1方法需要把區間長度10cM轉換成重組率0.0906[17]。模型中參數選取使得遺傳力在0.05和0.2附近。群體對QTL的影響很大，取定樣本容量為500。為了評價估計的準確度，給出了每個參數的均方誤差MSE。表2給出的是樣本量為500，遺傳力為0.2、0.05時MT-MIM-BC1方法與MT-MIM方法對QTL加性效應和顯性效應的估計值和MSE。模擬結果顯示在相同的遺傳力條件下MT-MIM-BC1方法比MT-MIM方法的參數估計值更接近參數真值，MT-MIM-BC1方法對所有QTL加性效應和顯性效應估計值的MSE和小于MT-MIM方法所對應的MSE和。說明MT-MIM-BC1方法比MT-MIM方法估計的精確度更高。隨著遺傳力的降低，兩種方法的精準度都有所降低，但MT-MIM-BC1方法明顯好于MT-MIM方法。

表2 h2=0.2，0.05，QTL效應的估計值

表3給出的是遺傳力為0.05和0.2時QTL重組率估計值和兩個表型性狀協方差矩陣估計值以及相應參數MSE。QTL重組率是MT-MIM-BC1方法相對MT-MIM方法獨有的。MT-MIM-BC1方法給出了QTL重組率的顯性表達式，通過重組率能夠更精準定位QTL在染色體上位置。MT-MIM 方法無法直接計算QTL重組率，表3中MT-MIM 方法重組率估計值是根據Joehanes[15]文章提供的方法重新編寫的。程序中通過似然比LR定位QTL在染色體上位置，然后根據QTL位置及其所在區間上標記位點之間的距離得到重組率的估計值。從表3可以看出在相同的遺傳力條件下MT-MIM-BC1方法重組率的估計值比MT-MIM 方法轉化的重組率值更接近參數真值，估計的精度也比MT-MIM方法高。隨著遺傳力降低兩種方法對參數估計的精準度逐漸變差，但MT-MIM-BC1方法對參數估計的精準度明顯好于MT-MIM方法。兩種方法對，，參數的估計值相差不大，但MT-MIM-BC1方法的MSE小于MT-MIM方法，說明MT-MIM-BC1方法參數估計精確度更高。

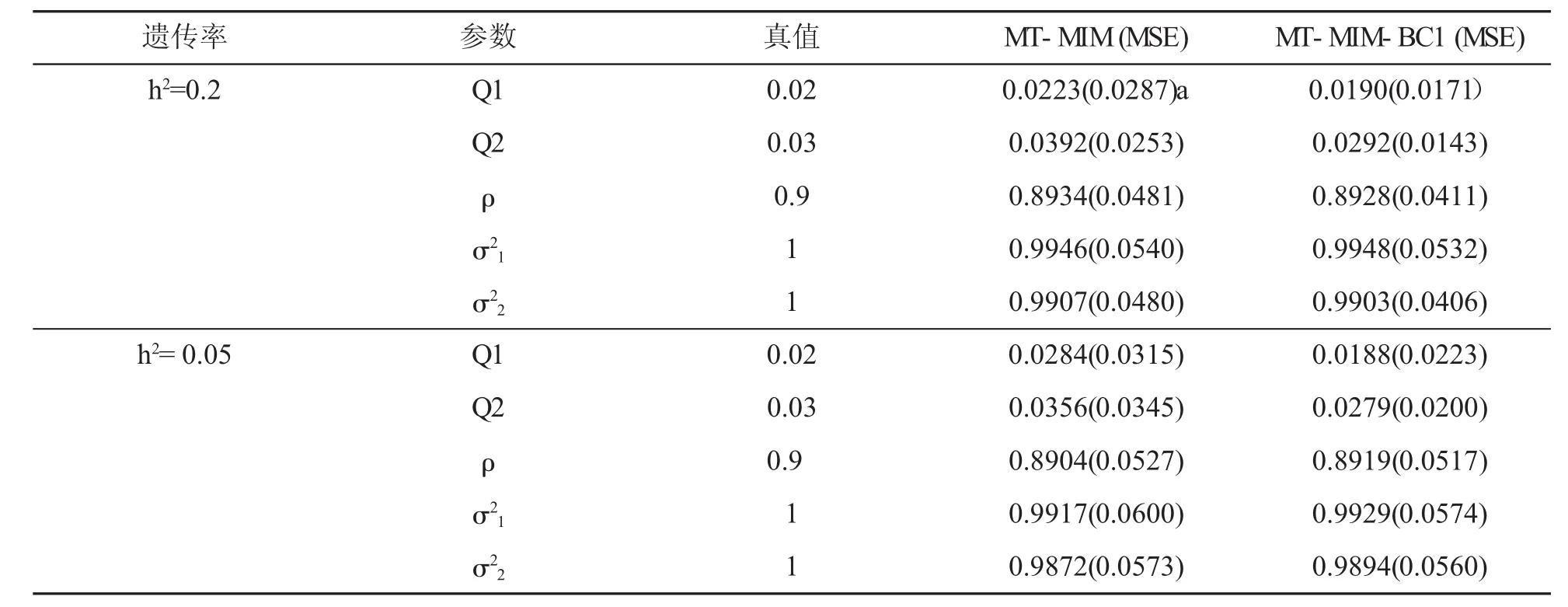
表3 h2=0.2，0.05，重組率和協方差估計值

MT-MIM-BC1方法選擇的模型把非遺傳標記位點效應也作為參數給出了其顯性表達式。表4給出的是在遺傳力為0.2和0.05條件下表型特征為T1和T2時非遺傳標記位點效應真值和估計值以及MSE。模擬結果顯示MT-MIM-BC1方法參數估計值比MT-MIM方法參數估計值更接近參數真值，MT-MIM-BC1方法所有標記位點效應的MSE和小于MT-MIM方法相應的MSE和。說明MT-MIM-BC1方法對標記位點效應估計的精確度高于MT-MIM方法。

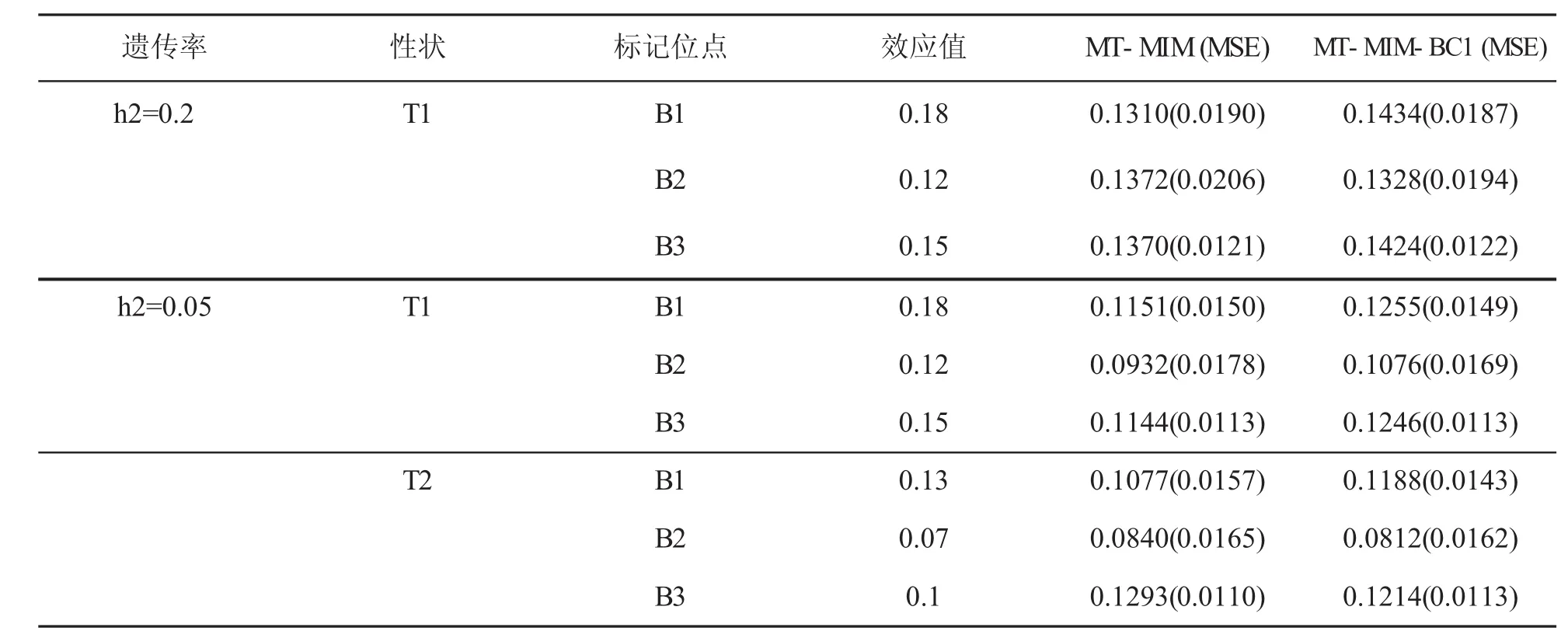
表4 h2=0.2，0.05，標記位點效應和MSE

三、結論與討論

本文是在MT-MIM方法的基礎上對BC1群體進行多性狀多區間定位（MT-MIM-BC1）。在不失一般性的條件下，我們對遺傳力為0.2、0.05，QTL個數和表型性狀個數為2進行了廣泛的模擬研究。研究結果表明MT-MIM-BC1方法相對MT-MIM方法參數估計的精準度更高。MT-MIM-BC1方法給出了重組率的顯性表達式，相對MT-MIM方法能夠更精準定位QTL到染色體上。

此外，獲得Ω的估計以后，我們可以研究QTL是否顯著存在。效應矩陣C的兩個假設可表示為

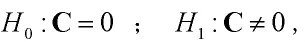
新方法的缺點同一般多區間定位方法一樣，當區間數比較多時，計算量非常大。由于基因定位在基因病的研究中起到至關重要作用，特別是有的基因具有多效性，多性狀多區間定位方法比多區間定位方法更具有優勢。在將來的工作中我們將進一步推廣，以便適應更多的標記位點。