具時滯的微分新古典增長模型正周期解的存在性
張孟孟 趙前進
(安徽理工大學(xué)數(shù)學(xué)與大數(shù)據(jù)學(xué)院 安徽淮南 232001)
近年來,隨著市場經(jīng)濟的發(fā)展,對市場經(jīng)濟模型的研究已經(jīng)成為數(shù)學(xué)經(jīng)濟學(xué)中廣泛討論的課題,其中對經(jīng)濟增長模型的定性和穩(wěn)定性分析引起諸多經(jīng)濟學(xué)家和數(shù)學(xué)家的廣泛關(guān)注和研究。例如,在文獻[1,2]中,Day最初研究了一類新古典增長模型、生產(chǎn)力和人口增長模型,研究表明即使在簡單的經(jīng)濟結(jié)構(gòu)下,也會有復(fù)雜的動力學(xué)行為出現(xiàn)。此后,關(guān)于復(fù)雜經(jīng)濟動力學(xué)的研究得到了越來越多的重視,參見[3-5]及相關(guān)參考文獻。
正如Matsumoto與Szidarovszky在文獻[6]中所述,為了更好地描述經(jīng)濟的長時間行為,根據(jù)經(jīng)濟學(xué)原理,建立新經(jīng)濟古典增長模型,主要基于如下兩個假設(shè):一是勞動力和資本的充分利用,二是輸出市場的及時調(diào)整。由于生產(chǎn)函數(shù)的合理選擇,模型的穩(wěn)態(tài)解通常是漸近穩(wěn)定的。然而,在現(xiàn)實世界中,經(jīng)濟學(xué)家觀察到經(jīng)濟增長路徑往往表現(xiàn)出持久震蕩性。因此,當(dāng)非線性項和生產(chǎn)時滯都存在的情況下,為更好地描述這種持久行為是如何出現(xiàn)的,新古典增長模型將成為一個很好的研究出發(fā)點。基于這一事實,Matsumoto與Szidarovszky在文獻[9]中提出了如下具有丘型生產(chǎn)函數(shù)的增長模型:

其中x是每個勞動力的資本,s∈(0,1)是平均儲蓄傾向,對于α=k+sμ,μ是資本的折舊率,k是勞工的增長率;丘型函數(shù)(a,b和 A是正系數(shù))是Cobb-Douglas式的,其中反映了由人均輸出造成的污染影響。考慮到在經(jīng)濟市場實現(xiàn)的過程中,時間上造成的延遲是不可避免的,同時還會受到自然環(huán)境和人為因素的影響,他們在文獻[6]中進一步提出了如下形式的經(jīng)濟模型:
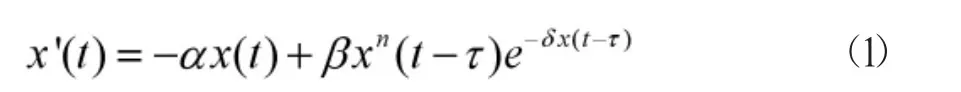
τ是運轉(zhuǎn)過程中產(chǎn)生的時滯,n可以被看作是測量生產(chǎn)函數(shù)規(guī)模的一個指標,δ反映了資本日益集中導(dǎo)致的“負面效應(yīng)”的強度,并由自然環(huán)境或能源資源的破壞性程度決定。顯然模型(1)是具有常時滯的一種具有非單調(diào)雙穩(wěn)態(tài)非線性的時滯微分方程,其具有兩個正平衡的吸引域和唯一不穩(wěn)定正平衡的收斂性,在黃創(chuàng)霞和鄭作環(huán)教授等的文獻[7,8]中得到了驗證。最近,當(dāng)0<n<1時,利用壓縮映射原理和Lyapunov方法,段煉和黃創(chuàng)霞研究了如下非自治具有多時滯的微分新古典增長模型的概周期解的存在性和全局吸引性:

我們知道,當(dāng)n=1時,模型(2)是著名的果蠅模型,諸多學(xué)者圍繞該模型展開了深入的研究,在其周期動力學(xué)方面已經(jīng)取得了很好的成果,例如文獻[10-13]。然而,在n>1的情況下,鮮有對模型(2)正周期解存在性的研究。
基于以上討論,我們利用微分不等式技巧和錐不動點定理,研究模型(2)在n>1的情況下其正周期解的存在性。為了方便,我們首先給出如下假設(shè):和都是T周期函數(shù),其中i=1,2…,m,并記。
一、預(yù)備知識
在這一部分,我們給出在本文中運用到的記號、定義和引理。對于一個連續(xù)的正T周期函數(shù)f(t),定義為為

我們?nèi)〕跏紬l件

這里 τ*=max τi+容易證明初值問題(2)和(3)在 t∈[0,∞]上有一個非負解 x(t)且對于 t≥τ* 有 x(t)>0。
定義1 令X是一個Banach空間,P是X的一個非空閉集。若有
(1)對任意的 x,y∈P,a,b≥0 都有 ax+by∈P,
(2)當(dāng)x,-x∈P時,x=0成立,則稱P是X的一個錐。
引理1(Krasnosekill錐不動點定理[14])設(shè)X是一個Banach空間,P?X是X中的一個錐。Ω1和Ω2是X中的開閉集且令
(1) 對 x∈P∩?Ω1,有 ||AX||≥||x||;對 x∈P∩?Ω2,有||AX||≤||x||;或者
(2) 對 x∈P∩?Ω1,有 ||AX||≤||x||;對 x∈P∩?Ω2,有||AX||≥||x||成立,則 A在 P∩上必有不動點。
二、主要結(jié)果
則x在賦予范數(shù)||·||下為Banach空間。若x(t)∈X是方程(2)的一個正周期解,則有
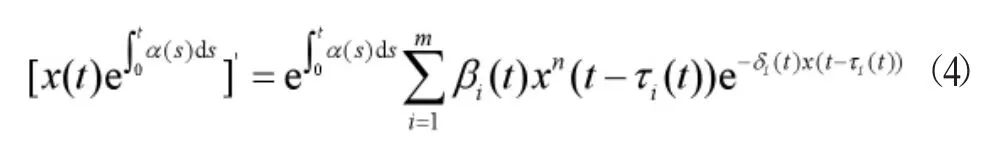
對(4)式兩邊在[t,t+T]上積分可得
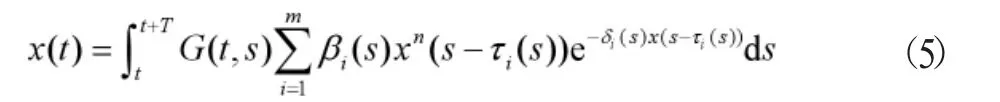


顯然P是X的一個錐。定義算子A:X→X,則

對于 X∈P,t∈[O,T],有

因此,AP?P。
引理2 假設(shè)(H)成立,則A:P→P是全連續(xù)的。
證明 顯然,A在[1,∞]是連續(xù)的且對任意地X∈P,t∈R+有


因此,{Ax:x∈P}是一類一致有界且等度連續(xù)的函數(shù)。由Ascoli-Arzela定理可知A:P→P,具有緊性,繼而,A:P→P是全連續(xù)的。引理2得證。
引理3 假設(shè)(H)成立,令
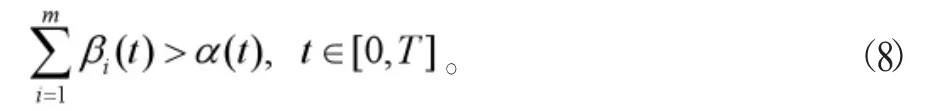
則對于任意的x∈P,存在正常數(shù)A,B使得下列不等式成立
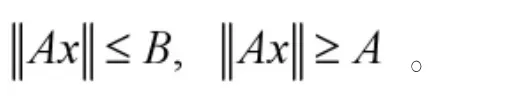
證明 由(7)知,對于任意的 x∈P,t∈R+有
由(8)成立,則可以找到一個適當(dāng)?shù)摩茫?使得下列不等式成立
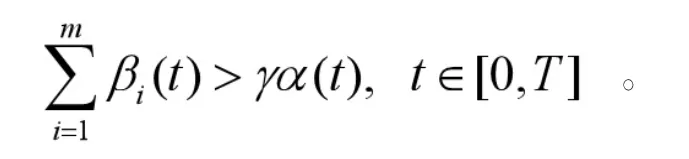
對于任意的 x∈P,t∈R+,有

比較(5)和(6)兩式可知,對于任意的 x∈P,t∈R+,我們有
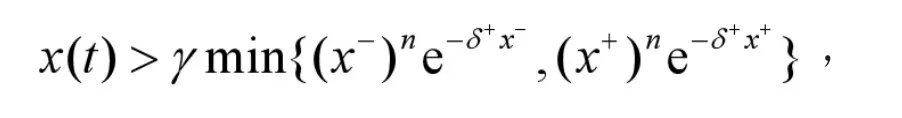
這就意味著

根據(jù)(7)同理可得,x(t)≤B,這就意味著 x+≤B。

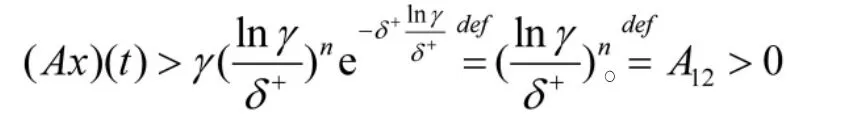
三、應(yīng)用舉例
考慮如下具時滯的微分新古典增長模型

注記 本文中,我們考慮了時所考慮模型周期解的存在性。由于時,周期解可作特殊概周期解來研究,文獻[5]已建立了很好的充分條件并驗證了概周期解的存在性。我們知道,當(dāng)時,模型(2)是著名的Nicholson果蠅模型,學(xué)者圍繞該模型展開了深入的研究,在其周期解存在性的充分條件上已經(jīng)取得了很多成果。據(jù)作者所知,對一類具時滯的微分新古典增長模型關(guān)于的周期解存在性的研究還很少見,因此本文的結(jié)論推廣并補充了已有文獻的結(jié)果。本文我們只研究了模型(2)周期解存在性的充分條件,對其感興趣的學(xué)者還可繼續(xù)研究其穩(wěn)定性和全局吸引性的相關(guān)結(jié)論。
四、結(jié)語
本文利用微分不等式技巧和錐不動點理論驗證了一類具時滯的微分新古典增長模型正周期解的存在性,判據(jù)新穎改進并推廣了已有文獻的相關(guān)結(jié)論,同時為經(jīng)濟學(xué)工作者提供了強有力地理論依據(jù)。

